-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Statistics and Applications
p-ISSN: 2168-5193 e-ISSN: 2168-5215
2017; 7(2): 57-72
doi:10.5923/j.statistics.20170702.02

The Variance Weighted Gradient Projection (VWGP): An Alternative Optimization Approach of Response Surfaces
Otaru O. A. P., Iwundu M. P.
Department of Mathematics and Statistics, University of Port Harcourt, Port Harcourt, Nigeria
Correspondence to: Iwundu M. P., Department of Mathematics and Statistics, University of Port Harcourt, Port Harcourt, Nigeria.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

A Variance Weighted Gradient Projection (VWGP) method that uses experimental design principles based on variance, and simultaneously optimizes several response surfaces is introduced as an alternative to popularly used one-at-a-time optimization methods. The method relies on the general line search equation whose components are the starting (initial) point of search, the direction of search, the step-length and the point arrived at the jth iteration. At the end of an iteration, the optimizer(s) reached are successively added to the previous immediate design measure(s). The use of projection operator scheme that allows the projection of design points from one design space to another is employed. Unlike most existing optimization methods which use guess initial point of search, a weighted average of design points selected from the design region and sufficiently spread over the entire region, is proposed as the initial point of search. By the choice of the proposed initial point of search, two limitations of the guess point methods are overcome, namely cycling and possible lack of convergence. Results obtained using the VWGP simultaneous optimization method have been compared with the BFGS Quasi-Newton algorithm and the VWGP method is seen comparatively efficient in locating the optimizers of several response surfaces.
Keywords: Simultaneous Optimization, Response Surfaces, Variance Weighted Gradients, Projection Operator, Quasi-Newton’s Algorithm
Cite this paper: Otaru O. A. P., Iwundu M. P., The Variance Weighted Gradient Projection (VWGP): An Alternative Optimization Approach of Response Surfaces, International Journal of Statistics and Applications, Vol. 7 No. 2, 2017, pp. 57-72. doi: 10.5923/j.statistics.20170702.02.
Article Outline
1. Introduction
- The optimization of response surfaces plays a vital role in locating the best set of factor levels to achieve some goals. Scientists and researchers have explored Response Surface Methodology (RSM) in various areas such as chemical, manufacturing and processing industries, managerial studies, engineering and science disciplines, etc. RSM is essentially a sequential procedure and entails response surface designs, modeling and optimization. It usually explores the relationships between several explanatory variables and one or more response variables. The response model used is only an approximation to the true unknown model. In many practical situations, the need for a solution of a set of approximating polynomial response functions arises. Attempts have been made by several researchers to address the optimization of response surfaces. In fact, various gradient and non-gradient based optimization methods have been formulated to address the need. Some of the methods include Newton’s Method (NM), Quasi-Newton’s Method (QNM), Genetic Algorithm (GA), Particle Swarm Algorithm (PSA), Mesh Adaptive Direct Search Method, etc. Comparatively, the gradient methods seem to be faster than the non-gradient methods in terms of the required iterative steps to convergence. The Newton’s Method, which was developed by [7] optimizes polynomial functions when the functions are differentiable. Due to the computational rigour involved in the Newton’s method, [10] gave an improvement to the Newton’s Method thus overcoming the tedious computational challenges. For historical development of the Newton-Raphson method, see [11]. Quasi-Newton Methods are used as alternatives to the Newton’s method and are frequently used in Non-Linear Programming to improve the computational speed of the Newton’s method. The first Quasi Newton Method, though rarely used today, was developed by [2] and was later given attention by other researchers like [3]. Although the Quasi Newton Method has faster computational time than the Newton’s Method, the convergence rate is however still slow. The most commonly used Quasi Newton algorithms are the SR1 formular, the BHHH method and the BFGS. The BFGS Quasi Newton Method, suggested independently by Broyden, Fletcher, Goldfarb and Shanno (See [1]), is the method used in the mathematical software, MATLAB. Although having their drawbacks, Newton’s method as well as Quasi Newton Methods have been extensively and successfully used in single objective optimization problems as seen in [5] and [9]. As opposed to single-objective optimization problems, interests are moving deeply into multiobjective optimization problems involving two or more objective functions to be optimized simultaneously. For both single- and multiple-objective optimization problems, the use of gradient-based algorithms seem successfully utilized. [4] presented an extension of Newton’s method for solving unconstrained multiobjective optimization problems. One very recent paper on the subject of multiobjective optimization is due to [12]. The paper presented a quasi-Newton’s method for solving unconstrained multiobjective optimization problems when the objective functions are strongly convex. For the successes in using gradient-based algorithms, we present in this paper the Variance Weighted Gradient Projection (VWGP) method for simultaneously optimizing several response functions defined over different constraints and having disjoint feasible regions. The method is gradient-based, relying on weighted gradients of the response functions resulting from the variances of the design points. The method uses the properties of line equations, such as could be seen in [8] to obtain the optimum responses. The consideration for the Variance Weighted Gradient Projection algorithm stems from the successful use of the Variance Weighted Gradient algorithm in optimizing response surfaces defined over same feasible region and having same constraints as in [6]. In handling the problem involving different regions and different constraints, a projection scheme that allows the projection of design points from one design region to another is proposed. The projection scheme enhances fast convergence of the algorithm to the desired optima as measured by the number of iterative moves made. It is possible to have one or more response functions converge before others, however, all functions are certain to converge to the required optima.
2. Methodology
- The proposed method relies on the properties of line equation, having a starting point of search, a direction of search and a step length. The three parameters of the line search are optimally chosen.
2.1. The Starting Point of Search
- The starting point of search is obtained as the weighted mean of the selected design points from the design region, where the weighting factor is a function of the variance of the design points.For an N-point design measure,
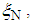 comprising of the design points
comprising of the design points 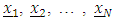 we define a weighted mean vector
we define a weighted mean vector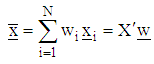 where,
where,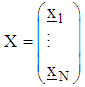 is an
is an 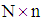 design matrix and
design matrix and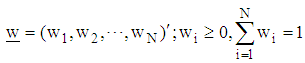 is the vector of weights associated with the design points.The optimal starting point
is the vector of weights associated with the design points.The optimal starting point 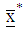 is obtained by minimizing the norm
is obtained by minimizing the norm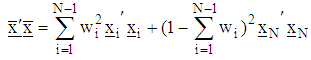 To minimize
To minimize 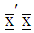 with respect to
with respect to 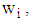 we solve
we solve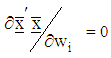 The optimal starting point of search is
The optimal starting point of search is 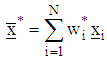
2.2. The Direction of Search
- The direction of search is in the direction of minimum variance and is computed as
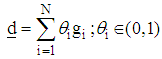 where
where 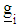 is the gradient vector and
is the gradient vector and 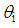 weighting factor vector.The direction variance is given as
weighting factor vector.The direction variance is given as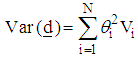 where
where 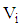 is the variance of the function at the ith support point. The weighting vector
is the variance of the function at the ith support point. The weighting vector 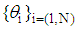 is obtained from the partial derivatives
is obtained from the partial derivatives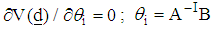 where
where 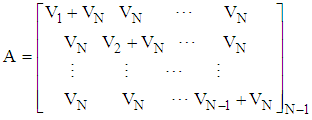
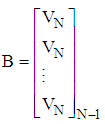 and
and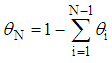 The normalized weighting factor vector
The normalized weighting factor vector 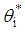 is given as
is given as 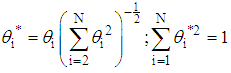
2.3. The Step Length of Search
- Given that the response function is constrained and the optimizer lies on the boundary of the feasible region governed by
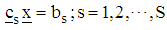 The optimal step-length
The optimal step-length 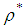 of the function
of the function 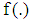 is obtained as the minimum distance covered in an average step for s number of constraint and is defined as:
is obtained as the minimum distance covered in an average step for s number of constraint and is defined as: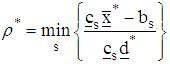 Where
Where 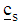 and
and 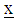 are vectors and
are vectors and 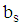 is a scalar for s number of constraints, while
is a scalar for s number of constraints, while 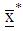 is the optimal starting point and
is the optimal starting point and 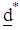 is the optimal direction vector.
is the optimal direction vector.2.4. The Variance Weighted Gradient Projection (VWGP) Approach
- Let
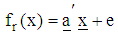 be the n-variate, p-parameter polynomial of degree m, defined on the rth feasible regions
be the n-variate, p-parameter polynomial of degree m, defined on the rth feasible regions 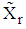 supported by s constraints. Such that
supported by s constraints. Such that 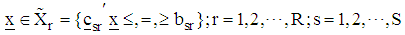 where
where 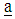 is a p-component vector of known coefficients, independent random variable
is a p-component vector of known coefficients, independent random variable 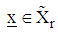 and
and 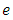 is the random error component assumed normally and independently distributed with zero mean and constant variance. While
is the random error component assumed normally and independently distributed with zero mean and constant variance. While 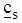 is a component vector of know coefficients and
is a component vector of know coefficients and 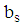 is a scalar for s number of constraints in the rth region.The Variance Weighted Gradient (VWG) method is given by the following sequential steps:i) From
is a scalar for s number of constraints in the rth region.The Variance Weighted Gradient (VWG) method is given by the following sequential steps:i) From 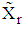 obtain the design measures
obtain the design measures 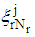 which are made up of support points from respective regions such that
which are made up of support points from respective regions such that 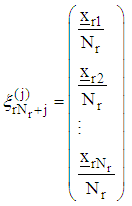 where
where 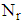 support points are spread evenly in
support points are spread evenly in 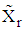 ii) From the support points that make up the design measure compute R starting points as, the arithmetic mean vectors.
ii) From the support points that make up the design measure compute R starting points as, the arithmetic mean vectors. 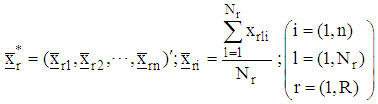 iii) Obtain the n-component gradient function for the rth region.
iii) Obtain the n-component gradient function for the rth region.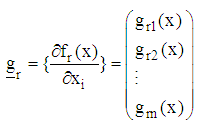 where
where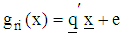 is an
is an 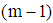 degree polynomial;
degree polynomial; 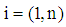
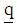 is a t-component vector of known coefficients iv) Compute the corresponding r gradient vectors, by substituting each design point defined on the rth region to the gradient function
is a t-component vector of known coefficients iv) Compute the corresponding r gradient vectors, by substituting each design point defined on the rth region to the gradient function 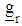 as
as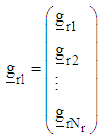 v) Using the gradient function and design measures obtain the corresponding design matrices
v) Using the gradient function and design measures obtain the corresponding design matrices 
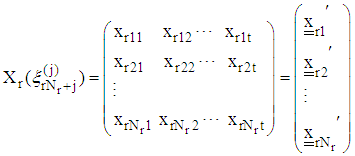 In order to form the design matrix
In order to form the design matrix 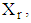 a single polynomial that combines the respective gradient function
a single polynomial that combines the respective gradient function 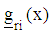 associated with each response function
associated with each response function 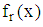 is
is 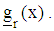 vi) Compute the variances of each l design point
vi) Compute the variances of each l design point 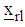 defined on the rth region as
defined on the rth region as 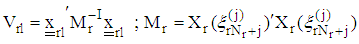 vii) Obtain the direction vector in the rth region as
vii) Obtain the direction vector in the rth region as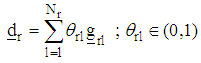 and the normalize direction vector
and the normalize direction vector 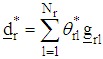 such that
such that 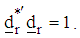 viii) Compute the step-length
viii) Compute the step-length 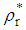 as
as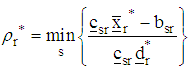 with
with 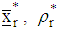 and
and 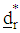 make a move to
make a move to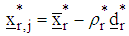 using
using 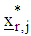 evaluate the projection operator
evaluate the projection operator 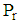 as
as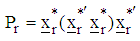 and obtain the projector optimizers for each region
and obtain the projector optimizers for each region 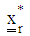 as
as 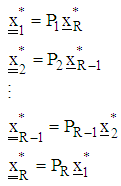 ix) To make a next move set
ix) To make a next move set 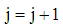 and define the design measure as
and define the design measure as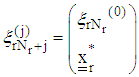 and repeat the process from step (ii) then obtain
and repeat the process from step (ii) then obtain 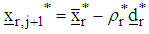 x) If
x) If 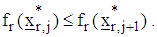 where
where 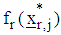 is the rth feasible region at the jth step and
is the rth feasible region at the jth step and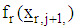 is the rth feasible region at the next j+1th step.then set the optimizers as
is the rth feasible region at the next j+1th step.then set the optimizers as 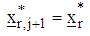 and STOP. Else, set
and STOP. Else, set 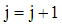 and repeat the process from (ii).Theorem Let the direction vector
and repeat the process from (ii).Theorem Let the direction vector 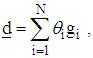 the weighting factor vector
the weighting factor vector 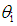 is inversely proportional to the variance vector of the function
is inversely proportional to the variance vector of the function 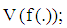 where
where 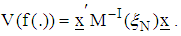 Proof: (By induction)
Proof: (By induction)
3. Results
- We present the working of the algorithm using a numerical illustration involving two response functions. The problem is;
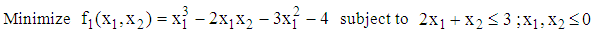 and
and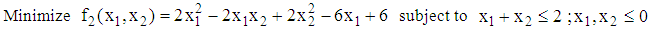 The design regions are defined by
The design regions are defined by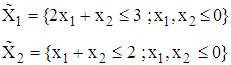 To solve this problem using the VWGP technique, we select design points from
To solve this problem using the VWGP technique, we select design points from  to make up the respective initial design measures as
to make up the respective initial design measures as Taking the weighted averages, the initial starting points for the two functions are, respectively,
Taking the weighted averages, the initial starting points for the two functions are, respectively,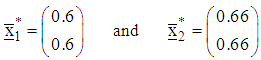 The gradient vectors are obtained as
The gradient vectors are obtained as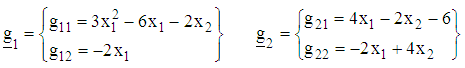 Hence the gradient functions are, respectively,
Hence the gradient functions are, respectively, 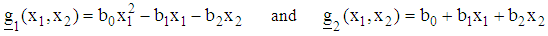 Using the gradient functions and the design measures, we form the corresponding design matrices as
Using the gradient functions and the design measures, we form the corresponding design matrices as The variances associated with the design points of each design measure are computed as illustrated below for the design point
The variances associated with the design points of each design measure are computed as illustrated below for the design point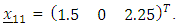 The variance of
The variance of 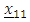 denoted
denoted 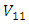 is computed as
is computed as The process continues similarly in obtaining the variance of each design point from the two regions. Thus the vectors of variances are respectively,
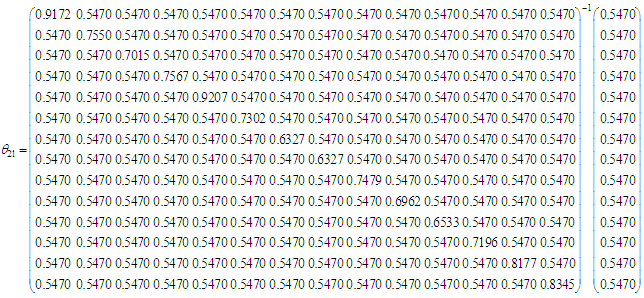
The process continues similarly in obtaining the variance of each design point from the two regions. Thus the vectors of variances are respectively,  The weighting factors are obtained as
The weighting factors are obtained as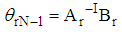 where
where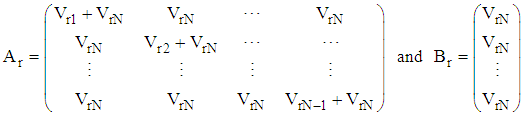 Thus
Thus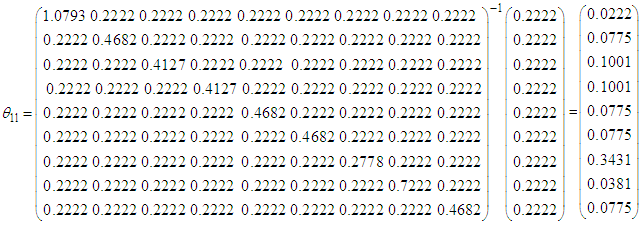 and
and 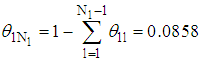
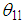 is normalized as
is normalized as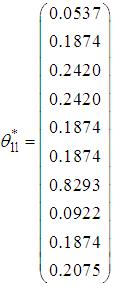
 Thus
Thus 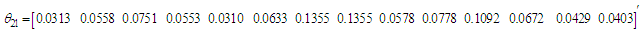 and
and 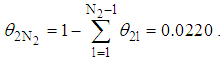
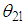 is normalized as
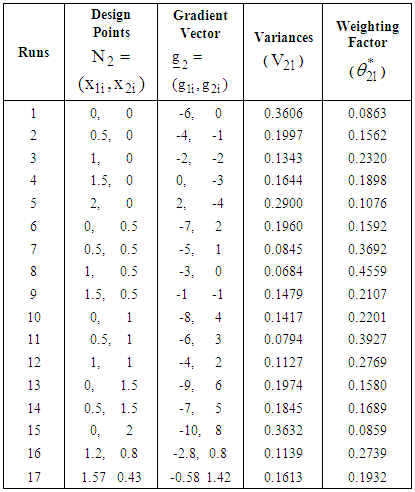
is normalized as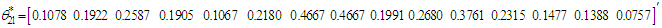 The computed statistics are summarized in Table 1.
The computed statistics are summarized in Table 1.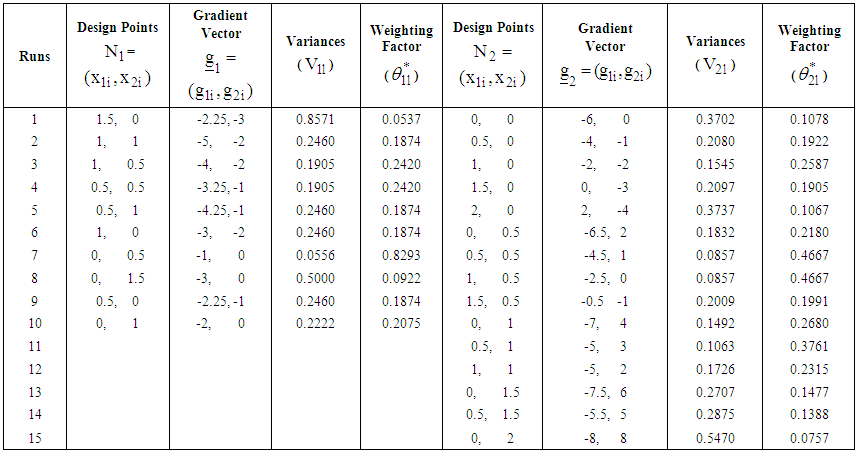 | Table 1. Summary statistics for the first and second response functions at respective design points in the first iteration |
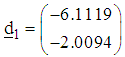 and
and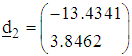 The normalized direction vectors are respectively
The normalized direction vectors are respectively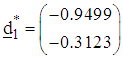 and
and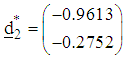 The associated step-lengths are computed as
The associated step-lengths are computed as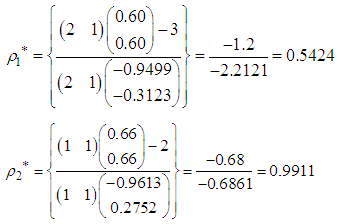 With the starting points of search, the directions of search and the step-lengths we make a first move for each of the functions to
With the starting points of search, the directions of search and the step-lengths we make a first move for each of the functions to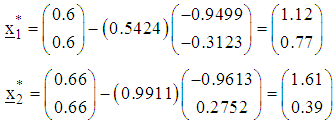
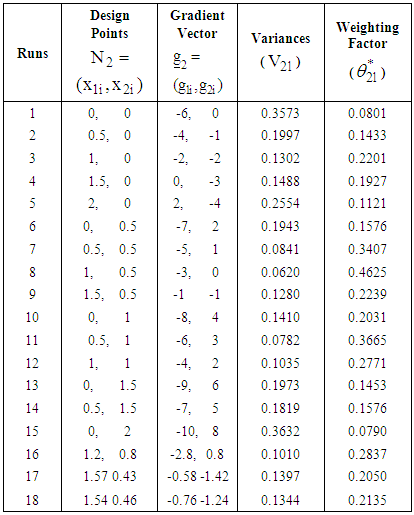
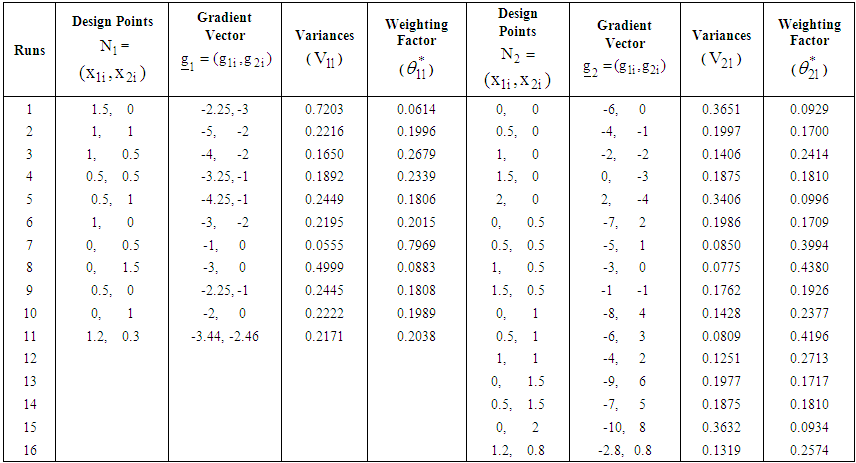 | Table 2. Summary statistics for the two response functions at respective design points in the second iteration |
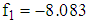 and
and 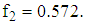 In order to make a second move, a projector operator
In order to make a second move, a projector operator 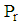 is formulated by projecting design points from one design space or feasible regions to another feasible region. The resulting projector operator
is formulated by projecting design points from one design space or feasible regions to another feasible region. The resulting projector operator  is used to compute the projector optimizers
is used to compute the projector optimizers 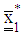 and
and 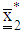 which are added to the design measure of respective response function and the process of search continues. The computations are as follows:
which are added to the design measure of respective response function and the process of search continues. The computations are as follows: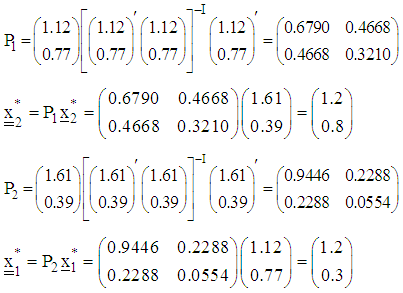 Adding the projector optimizers to the initial design measures result in the following augmented design measures
Adding the projector optimizers to the initial design measures result in the following augmented design measures With the new design measures, the computed statistics are summarized in Table 2.The starting points of search at the second iteration are respectively
With the new design measures, the computed statistics are summarized in Table 2.The starting points of search at the second iteration are respectively 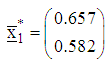 and
and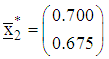 As previously described, the directions of search and the step-lengths of search at the second iteration are computed similarly as
As previously described, the directions of search and the step-lengths of search at the second iteration are computed similarly as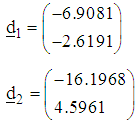 and normalized as
and normalized as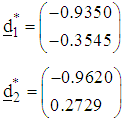 Compute the step-lengths of search are respectively
Compute the step-lengths of search are respectively 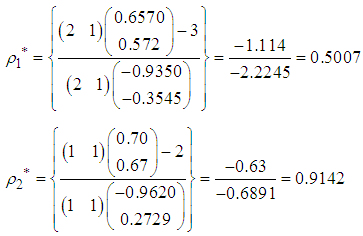 The points reached at the second iteration are respectively
The points reached at the second iteration are respectively 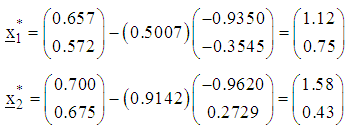 The corresponding values of objective functions are respectively
The corresponding values of objective functions are respectively 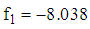 and
and 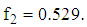 Since for the first function,
Since for the first function, 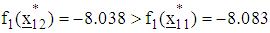 , convergence is established for the first function. However, since for the second function
, convergence is established for the first function. However, since for the second function 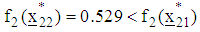
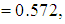 a next iteration is required. Using a projector operator, a new design point
a next iteration is required. Using a projector operator, a new design point 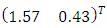 is obtained and thus the design measure is augmented as
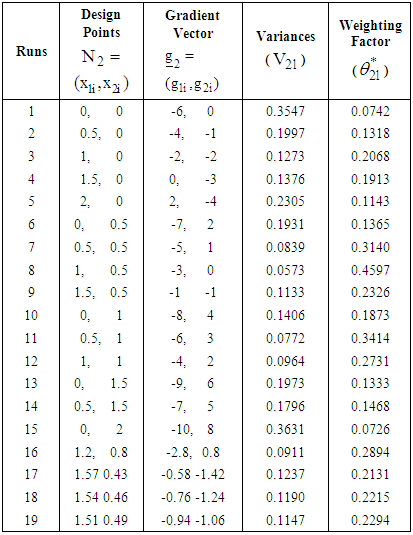
is obtained and thus the design measure is augmented as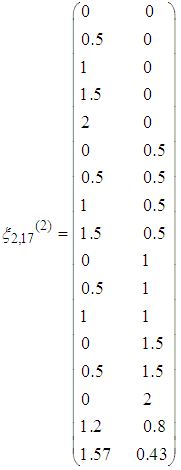 Continuing the process, the computed statistics using the new design measure are summarized in Table 3.
Continuing the process, the computed statistics using the new design measure are summarized in Table 3.
|
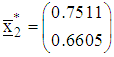 The direction of search, normalized direction of search and step-length of search at the third iteration are respectively
The direction of search, normalized direction of search and step-length of search at the third iteration are respectively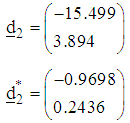 and
and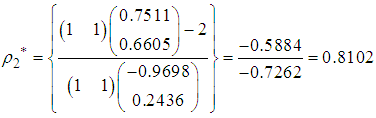 The point reached at the third iteration is
The point reached at the third iteration is 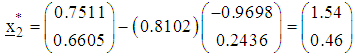 The corresponding value of objective function is
The corresponding value of objective function is 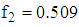 Since
Since 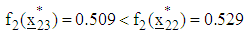 , a next iteration is required. Using a projector operator, a new design point
, a next iteration is required. Using a projector operator, a new design point 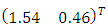 is obtained and thus the design measure is augmented as
is obtained and thus the design measure is augmented as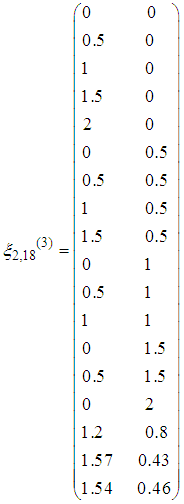 The computed statistics using the new design measure are summarized in Table 4.
The computed statistics using the new design measure are summarized in Table 4.
|
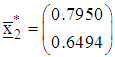 The direction of search, normalized direction of search and step-length of search at the fourth iteration are respectively
The direction of search, normalized direction of search and step-length of search at the fourth iteration are respectively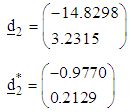 and
and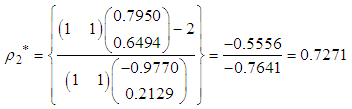 The point reached at the fourth iteration is
The point reached at the fourth iteration is 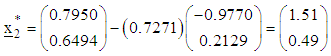 The corresponding value of objective function is
The corresponding value of objective function is 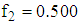 Since
Since 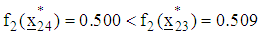 , a next iteration is required. Using a projector operator, a new design point
, a next iteration is required. Using a projector operator, a new design point 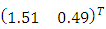 is obtained and thus the design measure is augmented as
is obtained and thus the design measure is augmented as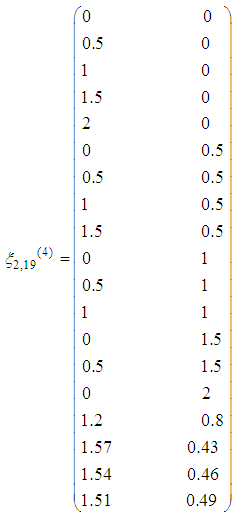 The computed statistics using the new design measure are summarized in Table 5.The starting point of search at the fifth iteration is
The computed statistics using the new design measure are summarized in Table 5.The starting point of search at the fifth iteration is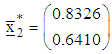 The direction of search, normalized direction of search and step-length of search at the fifth iteration are respectively
The direction of search, normalized direction of search and step-length of search at the fifth iteration are respectively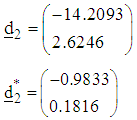 and
and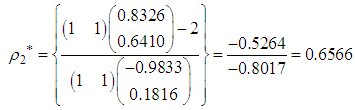 The point reached at the fifth iteration is
The point reached at the fifth iteration is 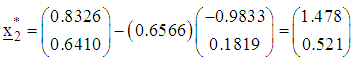 The corresponding value of objective function is
The corresponding value of objective function is 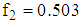 Since
Since 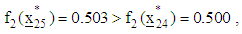 convergence is established and hence no indication for a further search.
convergence is established and hence no indication for a further search.
|
4. Discussion
- Variance is a principle commonly used in statistical theories. It has been used in design constructions as well as in optimization problems. Variances of direction vectors have been studied and it is well established that a good direction of search should satisfy the minimum variance property. In optimization, moving in the direction of minimum variance has been shown to optimize performance. This has been clearly stated and proved in literature. Available literatures also show advantage of moving in the direction of minimum variance. The use of variance principle in the VWGP algorithm employed in solving multi-objective problems has assisted in getting optimal solutions with possible minimum iterative moves. Also, optimal choices on the starting point of search and the step-length of search greatly enhanced performance. As mentioned in the literature review, various gradient and non-gradient based optimization methods have been formulated to obtain optimal solutions for constrained polynomial response functions defined over continuous variables. We have compared the solutions obtained using the new algorithm with those obtained using the Quasi-Newton method. With the Quasi-Newton method, results show that the function
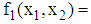
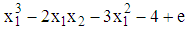 converged after four iterations with optimal values as
converged after four iterations with optimal values as 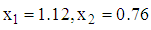 and a corresponding value of response function,
and a corresponding value of response function, 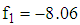 . Also using the Quasi-Newton method, the function
. Also using the Quasi-Newton method, the function 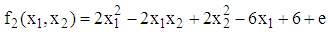 converged after four iterations with optimal values as
converged after four iterations with optimal values as 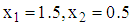 and a corresponding value of response function,
and a corresponding value of response function, 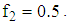 We observed that the guess initial point requirement of the Quasi-Newton method poses limitation in the use of the Quasi-Newton method. It is sometimes difficult to get a good guess point and thus results in slow convergence of the algorithm or even non-convergence of the algorithm. For the illustration presented in this paper, the optimal solution for the first function was found at the first iterative move and the optimal solution for the second function was found at the fourth iterative move. The printout from MATLAB showing the results are presented in Appendices A and B.The use of the Variance Weighted Gradient Projection (VWGP) method is a reliable optimization method for optimizing polynomial response surfaces defined by constraints on different feasible regions. The algorithm is reliable and converges to the desired optima with few iterative steps. The performance of the new algorithm agrees with the suggestion of [7] that a good algorithm should have less computation and a quick convergence. The present study may be extended to searching for optimal solutions to multi-objective functions defined on distinct regions but where some or all of the regions may have two or more objective functions.
We observed that the guess initial point requirement of the Quasi-Newton method poses limitation in the use of the Quasi-Newton method. It is sometimes difficult to get a good guess point and thus results in slow convergence of the algorithm or even non-convergence of the algorithm. For the illustration presented in this paper, the optimal solution for the first function was found at the first iterative move and the optimal solution for the second function was found at the fourth iterative move. The printout from MATLAB showing the results are presented in Appendices A and B.The use of the Variance Weighted Gradient Projection (VWGP) method is a reliable optimization method for optimizing polynomial response surfaces defined by constraints on different feasible regions. The algorithm is reliable and converges to the desired optima with few iterative steps. The performance of the new algorithm agrees with the suggestion of [7] that a good algorithm should have less computation and a quick convergence. The present study may be extended to searching for optimal solutions to multi-objective functions defined on distinct regions but where some or all of the regions may have two or more objective functions.5. Limitation of the Method
- The VWGP algorithm is not yet implemented in a Mathematical or Statistical software and hence the computation time and memory resources are not addressed.
ACKNOWLEDGEMENTS
- We sincerely wish to acknowledge the assistance and useful contributions of Professor I. B Onukogu of the Department of Mathematics and Statistics, University of Uyo, Nigeria.
Appendix 1
- The Quasi-Newton Optimization with the aid of MATLAB
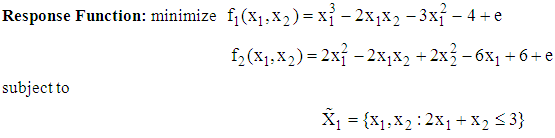 QN%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%Diagnostic Information Number of variables: 2
QN%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%Diagnostic Information Number of variables: 2 Algorithm selectedmedium-scale%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%End diagnostic information
Algorithm selectedmedium-scale%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%End diagnostic information Optimization terminated: magnitude of directional derivative in search direction less than 2*options.TolFun and maximum constraint violation is less than options.TolCon.Active inequalities (to within options.TolCon = 1e-006):
Optimization terminated: magnitude of directional derivative in search direction less than 2*options.TolFun and maximum constraint violation is less than options.TolCon.Active inequalities (to within options.TolCon = 1e-006):
Appendix 2
- The Quasi-Newton Optimization with the aid of MATLAB
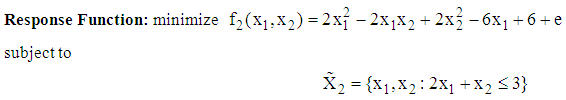 QN%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%Diagnostic Information Number of variables: 2
QN%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%Diagnostic Information Number of variables: 2 Algorithm selectedmedium-scale%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%End diagnostic information
Algorithm selectedmedium-scale%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%End diagnostic information Optimization terminated: first-order optimality measure less than options.TolFun and maximum constraint violation is less than options.TolCon.Active inequalities (to within options.TolCon = 1e-006):
Optimization terminated: first-order optimality measure less than options.TolFun and maximum constraint violation is less than options.TolCon.Active inequalities (to within options.TolCon = 1e-006):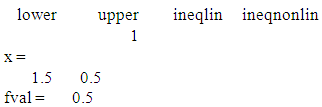
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML