Tarek Mahmoud Omara
Department of Statistics, Mathematics and Insurance, Faculty of Commerce, Kafrelsheikh University, Kafrelsheikh, Egypt
Correspondence to: Tarek Mahmoud Omara, Department of Statistics, Mathematics and Insurance, Faculty of Commerce, Kafrelsheikh University, Kafrelsheikh, Egypt.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper, we propose the MM and MM ridge estimators for SUR model to deal with outliers. The MM estimators are the type of robust regression with high breakdown point and have more efficient than other robust estimators. Since, outliers, frequently, appear with multicollinearity problem, then we propose MM ridge estimators for SUR mode. In these estimators, the shrink parameter was chosen by minimize robust Cross Validation Criteria (CVMM) which depend on MM estimators. This choice achieves high breakdown point for given shrink parameter. Therefore, the MM ridge estimator has strong robust features. In addition, the asymptotical properties for the MM and MM ridge estimators ware also investigated. The median ASE (average squared error) was used to compeer the efficiency for estimator and to compute the estimators we designed two algorithm. Furthermore, the Simulations study was executed to test the performance of GL S, S, MM and MM ridge estimators for SUR model.
Keywords:
Seemingly unrelated regression (SUR), GLS estimator, S-estimator, MM-estimator, MM ridge estimators, Robustness properties, Robust Cross Validation Criteria (CVMM)
Cite this paper: Tarek Mahmoud Omara, MM and MM Ridge Estimators for SUR Model, International Journal of Statistics and Applications, Vol. 7 No. 1, 2017, pp. 18-25. doi: 10.5923/j.statistics.20170701.03.
1. Introduction
The seemingly unrelated regression (SUR) Model proposed by (zellner, 1962) which it depends on general least squares estimator (GLS) and assumes data without outliers but in some cases this cannot be achieved. The robust methods considered the one important approach to deal with outliers which allow the unequal weight for observations. (Koenker etal, 1990) introduce M-estimators method, as a robust methods, to estimate SUR model when the data within outliers, yet the asymptotic efficiency for M-estimators depend on initial estimate and have breakdown point (bp) equal 0. Therefore, (Bilodeau etal., 2000) suggested S-estimator for SUR model which interest same asymptotic properties for M-estimators and have high (bp) reach to 50% of the observations. In the same side, (Garcia etal., 2006) and (Roelandt etal., 2009) proposed  for multivariate regression which have excellent robustness and high efficiency under normality of error. (Roelandt etal., 2009) extract generalized S estimates for multivariate regression which consider high breakdown estimation when analysis the independent component. The MM estimators for linear regression model was introduced by (Yohai, 1987)), which begin at the first with a highly initial robust regression estimator like S estimators which depend on a loss function
for multivariate regression which have excellent robustness and high efficiency under normality of error. (Roelandt etal., 2009) extract generalized S estimates for multivariate regression which consider high breakdown estimation when analysis the independent component. The MM estimators for linear regression model was introduced by (Yohai, 1987)), which begin at the first with a highly initial robust regression estimator like S estimators which depend on a loss function 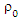 and then used this initial estimator to obtain M estimator with other loss function
and then used this initial estimator to obtain M estimator with other loss function 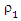 . This estimator has two advantage, the high asymptotic efficiency for normality error and high breakdown point reach to 50%. The study of (Berrendero etal., 2007) show that, the asymptotic bias for mm estimator is lower than the τ estimators when we contaminations error lower than 0.20 and the MM estimator has best lower maximum bias curve than other robust estimators. (Salibian etal., 2006) show that, the breakdown point of MM-estimator in finite-sample is equal to or greater than initial S-estimator. The MM estimators begin at the first with a highly initial robust regression estimator like S estimators which depend on a loss function
. This estimator has two advantage, the high asymptotic efficiency for normality error and high breakdown point reach to 50%. The study of (Berrendero etal., 2007) show that, the asymptotic bias for mm estimator is lower than the τ estimators when we contaminations error lower than 0.20 and the MM estimator has best lower maximum bias curve than other robust estimators. (Salibian etal., 2006) show that, the breakdown point of MM-estimator in finite-sample is equal to or greater than initial S-estimator. The MM estimators begin at the first with a highly initial robust regression estimator like S estimators which depend on a loss function 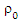 and then used this initial estimator to obtain M estimator with other loss function
and then used this initial estimator to obtain M estimator with other loss function 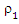 . (Kudraszow, 2011) suggested MM estimator for multivariate linear model and study the consistency and asymptotic normality with elliptical distribution for error. On other hand, frequently, outliers appear with degree of multicollinearity. The ridge method solved multicollinearity problem has been discussed by (Hoerl etal., 1970). This method is a way of proceeding in solving the problem by adding specific information to remove the ill-condition. The SUR model possibly is under the influence of multicollinarity. (Srivastava etal., 1987) suggested general ridge estimator to remove the ill-condition in SUR model (Alkhamisi. etal, 2006) developed ridge estimators of the SUR model, when the data are transformed in a canonical form. The critical point in ridge estimate is how to choose the shrink parameter. So, (Firinguetti, 1997), (Kibria etal., 2003) and (Alkhamisi. etal, 2006) suggested non robust Criteria to choice the shrink parameter in ridge estimator for SUR model. These formulas assume choosing ridge parameter when data without outliers. (Jung, 2009) proposed robust cross validation in ridge regression when data are within outliers. (El-hosany etal., 2011) used robust Cross Validation Criteria to choice shrink parameter in SUR model.In fact, frequently, outliers appear with degree of multicollinearity. Therefore, (El-hosany etal., 2011) mingle between ridge estimator and S- estimator to get robust ridge estimator. (Maronna, 2011), (Moawad etal., 2011) and (Mariam. etal., 2012) have developed MM-estimators to deal with leverage point and absorption problem of multicollinearity. This estimators builded by combined between ridge regression and mm-type to reach to mm ridge estimators. There is no study use the MM estimator in the SUR model. So, we suggests, MM and MM ridge estimator for SUR model to deal with bad high leverage points and the multicollinearity problem associated with it. In MM ridge estimator, we develop robust Cross Validation Criteria, to choice shrink parameter, depended on MM estimator. This paper organized as follows: The SUR model and estimators defined in Section two. In section three, we study the asymptotic properties of MM and MM ridge estimators in SUR model while section four will be devoted to make the simulation study. In section five, we develop algorithm to compute MM and MM ridge estimator for SUR model.
. (Kudraszow, 2011) suggested MM estimator for multivariate linear model and study the consistency and asymptotic normality with elliptical distribution for error. On other hand, frequently, outliers appear with degree of multicollinearity. The ridge method solved multicollinearity problem has been discussed by (Hoerl etal., 1970). This method is a way of proceeding in solving the problem by adding specific information to remove the ill-condition. The SUR model possibly is under the influence of multicollinarity. (Srivastava etal., 1987) suggested general ridge estimator to remove the ill-condition in SUR model (Alkhamisi. etal, 2006) developed ridge estimators of the SUR model, when the data are transformed in a canonical form. The critical point in ridge estimate is how to choose the shrink parameter. So, (Firinguetti, 1997), (Kibria etal., 2003) and (Alkhamisi. etal, 2006) suggested non robust Criteria to choice the shrink parameter in ridge estimator for SUR model. These formulas assume choosing ridge parameter when data without outliers. (Jung, 2009) proposed robust cross validation in ridge regression when data are within outliers. (El-hosany etal., 2011) used robust Cross Validation Criteria to choice shrink parameter in SUR model.In fact, frequently, outliers appear with degree of multicollinearity. Therefore, (El-hosany etal., 2011) mingle between ridge estimator and S- estimator to get robust ridge estimator. (Maronna, 2011), (Moawad etal., 2011) and (Mariam. etal., 2012) have developed MM-estimators to deal with leverage point and absorption problem of multicollinearity. This estimators builded by combined between ridge regression and mm-type to reach to mm ridge estimators. There is no study use the MM estimator in the SUR model. So, we suggests, MM and MM ridge estimator for SUR model to deal with bad high leverage points and the multicollinearity problem associated with it. In MM ridge estimator, we develop robust Cross Validation Criteria, to choice shrink parameter, depended on MM estimator. This paper organized as follows: The SUR model and estimators defined in Section two. In section three, we study the asymptotic properties of MM and MM ridge estimators in SUR model while section four will be devoted to make the simulation study. In section five, we develop algorithm to compute MM and MM ridge estimator for SUR model.
2. GLS, S, MM and Weight MM Estimator for SUR Model
Conceder the SUR model 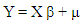 | (1) |
where 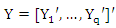 is a nq × 1 vector of dependant variable in q equation,
is a nq × 1 vector of dependant variable in q equation, 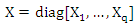 is a nq×kq matrix of independent variable and
is a nq×kq matrix of independent variable and 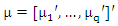 is a nq × 1 vector of random error in q equation. Suppose
is a nq × 1 vector of random error in q equation. Suppose 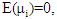
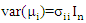 for all i=1,2,…q and
for all i=1,2,…q and 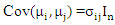 for all i,j=1,2,…q. We can right the SUR model in the multivariate form
for all i,j=1,2,…q. We can right the SUR model in the multivariate form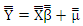 | (2) |
where 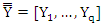 is a matrix of n q observations with
is a matrix of n q observations with 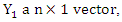
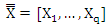 , is a
, is a 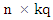 matrix,
matrix, 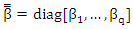 is a kq×q matrix of coefficients. and
is a kq×q matrix of coefficients. and 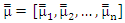 is a nq matrix of residual with
is a nq matrix of residual with 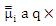
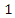 vector. Let
vector. Let 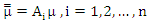 where
where 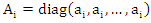 is a
is a 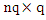 matrix and
matrix and 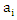 is vector contains one at position i and zero elsewhere. (Srivastava and Giles, 1987) suggested the GLS estimator for SUR model
is vector contains one at position i and zero elsewhere. (Srivastava and Giles, 1987) suggested the GLS estimator for SUR model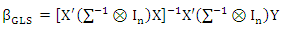 | (3) |
where 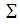 is q×q variance covariance matrix for error between equations. The GLS estimator calculate by use
is q×q variance covariance matrix for error between equations. The GLS estimator calculate by use 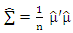 as consistent estimator for
as consistent estimator for 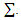 (Bilodeau etal, 2000) introduce S estimator to deal with outliers for SUR model. This estimator used the Huber function at the form
(Bilodeau etal, 2000) introduce S estimator to deal with outliers for SUR model. This estimator used the Huber function at the form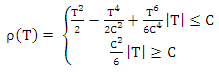 | (4) |
where 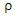 is symmetric, continuous, differentiable and for
is symmetric, continuous, differentiable and for 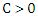 it is strictly increasing on [0; c], constant on [c,∞] and ρ(0)= 0. The percentage of breakdown point depend on C. (Ruppert, 1992) show that, when choice C=1.5476 the of breakdown point reach to 50%. The S estimator for SUR model minimize
it is strictly increasing on [0; c], constant on [c,∞] and ρ(0)= 0. The percentage of breakdown point depend on C. (Ruppert, 1992) show that, when choice C=1.5476 the of breakdown point reach to 50%. The S estimator for SUR model minimize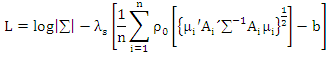 where
where 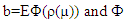 is the standard normal distribution. The S estimator satisfy the following equation
is the standard normal distribution. The S estimator satisfy the following equation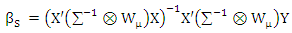 | (5) |
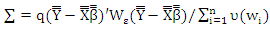 | (6) |
Where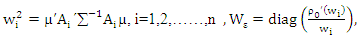
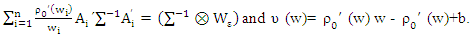 Lemma (1): Let the
Lemma (1): Let the 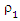 and
and 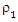 have symmetric, continuous, differentiable, for
have symmetric, continuous, differentiable, for 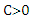 it is strictly increasing on [0; c], constant on [c,∞] and ρ(0)= 0. In adding, the function ρo and ρ1 achieve ρ1 (µ) ≤ ρo (µ) and Sup ρ1 (µ) = Sup ρ0 (µ). We use Huber function at the form (4). In the SUR model in (1). We can extracted the MM-estimator for SUR model (new) by
it is strictly increasing on [0; c], constant on [c,∞] and ρ(0)= 0. In adding, the function ρo and ρ1 achieve ρ1 (µ) ≤ ρo (µ) and Sup ρ1 (µ) = Sup ρ0 (µ). We use Huber function at the form (4). In the SUR model in (1). We can extracted the MM-estimator for SUR model (new) by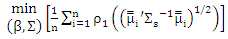 | (7) |
Where, 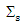 estimated by
estimated by 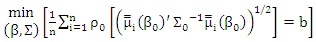 | (8) |
Where 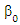 and
and 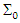 are initial estimators.Then the MM-estimator for SUR model satisfy the following equations
are initial estimators.Then the MM-estimator for SUR model satisfy the following equations 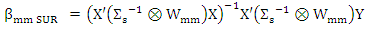 | (9) |
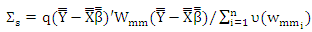 | (10) |
Where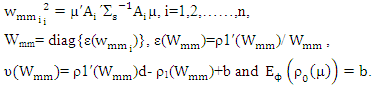 Proof of lemma (1)If we differentiate (7) with respect to β and equalize the result to zero then
Proof of lemma (1)If we differentiate (7) with respect to β and equalize the result to zero then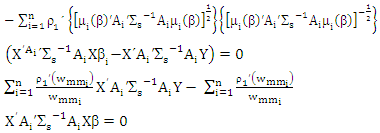 Where
Where 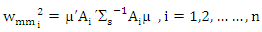 Then
Then 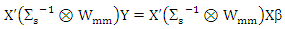 Where
Where 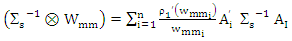 and
and 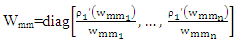 Then complete the proof.Lemma (2) If
Then complete the proof.Lemma (2) If 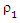 and
and 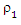 satisfy the condition in lemma (1), then we extract MM ridge estimator for SUR model (new) by
satisfy the condition in lemma (1), then we extract MM ridge estimator for SUR model (new) by 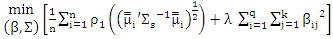 | (11) |
Where,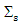 estimated by (8) and
estimated by (8) and 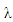 is ridge parameter. The MM ridge estimator for SUR model (new) in (1) can be written as
is ridge parameter. The MM ridge estimator for SUR model (new) in (1) can be written as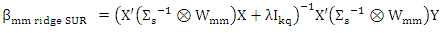 | (12) |
Proof of lemma (2)If we differentiate (11) with respect to β and equalize the result to zero then: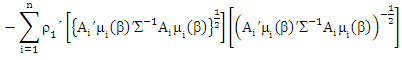
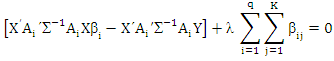
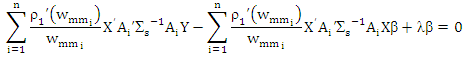 Then complete the proof.
Then complete the proof.
3. Asymptotic Properties for MM and MM Ridge Estimators for SUR Model
In this section, we study the asymptotic properties MM and MM ridge estimators.Lemma (3)Consider the SUR model with 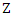 observe,
observe, 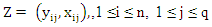 which independent random vectors distributed as pq-variate normal distribution
which independent random vectors distributed as pq-variate normal distribution 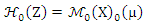 with mean μ= Zβ and variance ∑s, where
with mean μ= Zβ and variance ∑s, where 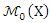 is distribution of X and
is distribution of X and 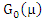 is distribution of µ.Then
is distribution of µ.Then
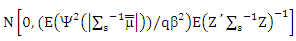 Where
Where 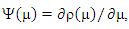
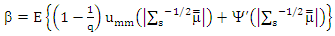 Proof of lemma (3):We use the proof for the Theorem (4-1) in (Yohai, 1987) and the asymptotical properties for S-estimator for SUR model in (Bilodeau etal, 2000) to access the prove. The MM-estimator of
Proof of lemma (3):We use the proof for the Theorem (4-1) in (Yohai, 1987) and the asymptotical properties for S-estimator for SUR model in (Bilodeau etal, 2000) to access the prove. The MM-estimator of 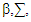 in SUR model, can be defined as a solution of M-type equation, then the anther form for equations (8) and (9) are
in SUR model, can be defined as a solution of M-type equation, then the anther form for equations (8) and (9) are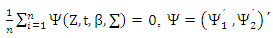 | (14) |
Where: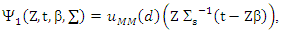
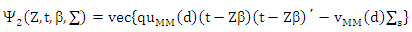 By using Mean Value Theorem (MVT),
By using Mean Value Theorem (MVT),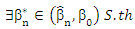
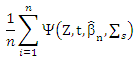
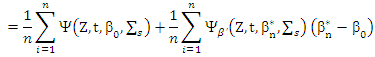 For (14)
For (14) 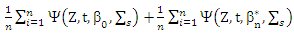
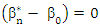 Then
Then 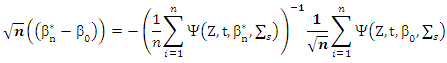 For uniform laws of large numbers (ULLN)
For uniform laws of large numbers (ULLN)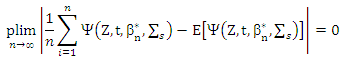
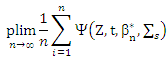
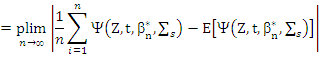
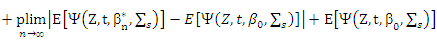 By central limit theorem (CLT), we get
By central limit theorem (CLT), we get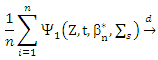
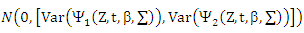 And then
And then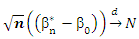
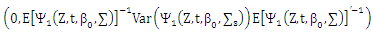 Under the assumption u elliptical. We study the asymptotic variance for
Under the assumption u elliptical. We study the asymptotic variance for 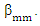 Hence
Hence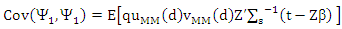
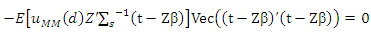 Let:
Let: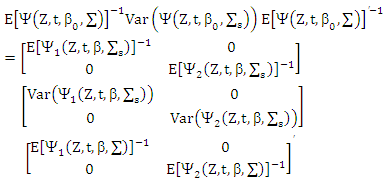 while
while 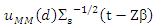 is spherical then
is spherical then 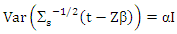
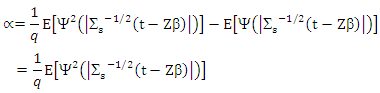 and then
and then 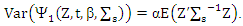 Extension for Lemma (5-1) (Lopuhaa, 1989). We get
Extension for Lemma (5-1) (Lopuhaa, 1989). We get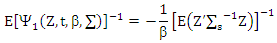 Where
Where 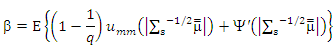 Then
Then 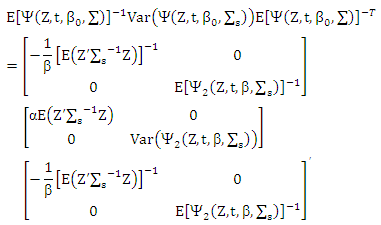 Then
Then 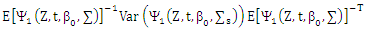
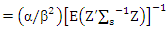 Then completes the proof.Lemma (4):Consider the same condition in proposition (3-1) and
Then completes the proof.Lemma (4):Consider the same condition in proposition (3-1) and 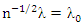 then
then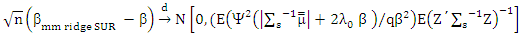 | (15) |
Where 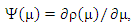
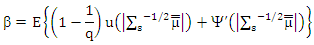 and then
and then 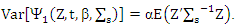 Following by the proof for lemma (3) then completes the proof.
Following by the proof for lemma (3) then completes the proof.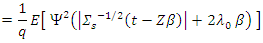 Where
Where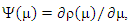
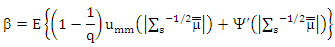 and
and 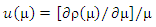 Proof of lemma (4):The MM ridge estimator of β,∑, in SUR model, can be defined as a solution of M-type equation, then the anther form for equations (9) and (12) are
Proof of lemma (4):The MM ridge estimator of β,∑, in SUR model, can be defined as a solution of M-type equation, then the anther form for equations (9) and (12) are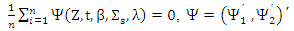 | (16) |
Where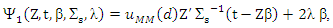
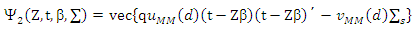 By using (MVT, (ULLN) and (CLT)) theorem in proofs for proportion (3-2). In adding, consider the condition
By using (MVT, (ULLN) and (CLT)) theorem in proofs for proportion (3-2). In adding, consider the condition 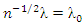 then
then 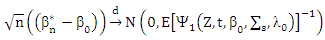
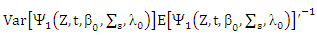 Under the assumption u elliptical. We study the asymptotic variance for
Under the assumption u elliptical. We study the asymptotic variance for 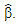 Hence
Hence 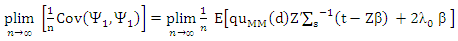 Let:
Let: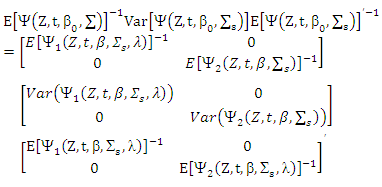 While
While 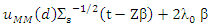 is spherical then
is spherical then 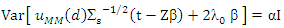 Where
Where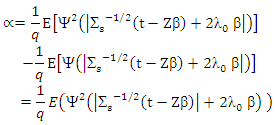 and then
and then 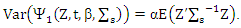 Following by the proof for lemma (3) then completes the proof.
Following by the proof for lemma (3) then completes the proof.
4. The Simulation Study
In this section, we provide a simulation study to illustrate the performance of four estimators, the (GLS), S, MM and MM ridge estimator for SUR model. This simulation process is executed to generate data for the following equation 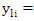
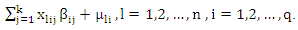 Where
Where 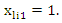 In this simulation, we set the initial value for β= [1,2,3] for k=3. The explanatory variables are generated by multivariate normal distribution MNNk=3 (0,∑x) where diag(∑x)=1, off-diag(∑x)= ρX= 0.15 for low interdependency and ρx= 0.70 for high interdependency. Where ρx is correlation between explanatory variables. We chose two sample size 25 for small sample and 100 for large sample. The specific error in equations μi, i=1,2,…..,n, we generated by MVNk=3 (0, ∑ε), ∑ε the variance covariance matrix of errors, diag(∑ε)= 1, off-diag(∑ε)= ρε= 0.15. To investigate the robustness of the estimators against outliers, we chosen different percentages of outliers ( 20%, 45%). We choose shrink parameter in (12) by minimize the new robust Cross Validation (CVMM) criterion which avoided outliers. This criterion depend on MM estimators and takes the form
In this simulation, we set the initial value for β= [1,2,3] for k=3. The explanatory variables are generated by multivariate normal distribution MNNk=3 (0,∑x) where diag(∑x)=1, off-diag(∑x)= ρX= 0.15 for low interdependency and ρx= 0.70 for high interdependency. Where ρx is correlation between explanatory variables. We chose two sample size 25 for small sample and 100 for large sample. The specific error in equations μi, i=1,2,…..,n, we generated by MVNk=3 (0, ∑ε), ∑ε the variance covariance matrix of errors, diag(∑ε)= 1, off-diag(∑ε)= ρε= 0.15. To investigate the robustness of the estimators against outliers, we chosen different percentages of outliers ( 20%, 45%). We choose shrink parameter in (12) by minimize the new robust Cross Validation (CVMM) criterion which avoided outliers. This criterion depend on MM estimators and takes the form 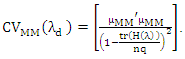 Where
Where 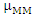 is a residual depend on MM estimators and
is a residual depend on MM estimators and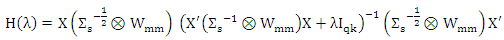 We measure the goodness of fit of estimated model for β by use the median average squared error [Median(ASE_j)] where ASE_j is defined by
We measure the goodness of fit of estimated model for β by use the median average squared error [Median(ASE_j)] where ASE_j is defined by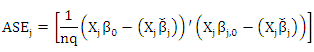 where j=1,2,……N. Where
where j=1,2,……N. Where 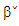 is MM estimator for β and N is a number of iteration. We run N=1,2,…, 500 replications by using software MATHCAD.
is MM estimator for β and N is a number of iteration. We run N=1,2,…, 500 replications by using software MATHCAD.
5. Algorithm
In this paper, we use two algorithm to compute the MM and MM ridge estimators. 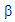 and
and 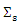 is initial estimate for
is initial estimate for 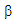 and
and 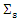 respectively, then iterative solve for (9) is
respectively, then iterative solve for (9) is 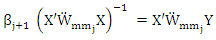 | (16) |
And the then iterative solve for (12) is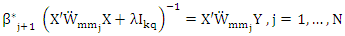 | (17) |
Where N is a number of iteration,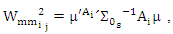
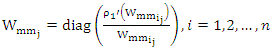
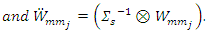 The equation (17) is a weight version for ridge estimator. This equation is rewrite as normal equations
The equation (17) is a weight version for ridge estimator. This equation is rewrite as normal equations 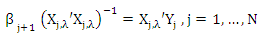 | (18) |
Where N is a number of iteration,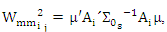
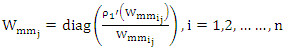 and
and 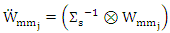 The equation (14) is a weight version for ridge estimator. This equation is rewrite as normal equations
The equation (14) is a weight version for ridge estimator. This equation is rewrite as normal equations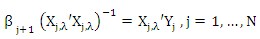 | (15) |
Where 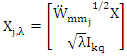 and
and 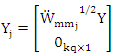 Algorithm (1)In this algorithm, we compute MM estimators for SUR model
Algorithm (1)In this algorithm, we compute MM estimators for SUR model  by developed the algorithms for (Tharmaratnam et al., 2008) and (Al-hosany et al., 2011) We drawing the algorithm (1) by the following steps:Step (1): Let
by developed the algorithms for (Tharmaratnam et al., 2008) and (Al-hosany et al., 2011) We drawing the algorithm (1) by the following steps:Step (1): Let 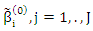 is initial candidates estimate for β.Step (2): Design the variable
is initial candidates estimate for β.Step (2): Design the variable 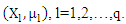 For each
For each 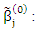 a. Compute
a. Compute 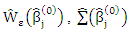 b. Compute S estimators as in (8) for some ρ-function ρ0 by set m=0, and get the following steps:i. Let
b. Compute S estimators as in (8) for some ρ-function ρ0 by set m=0, and get the following steps:i. Let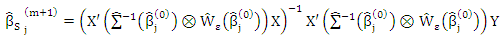 ii. If either m equal the maximum number of iterationsor
ii. If either m equal the maximum number of iterationsor 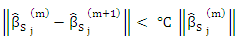 where
where 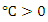 is affixed smalliii. constant, then
is affixed smalliii. constant, then 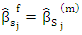 go to step (2)iv. Else Compute
go to step (2)iv. Else Compute 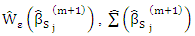 , and put m←m+1Step (3): Select
, and put m←m+1Step (3): Select 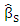 which active
which active 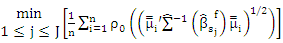 Step (4): Compute MM estimator as in (7) for some ρ-function ρ1: Let g=0 and compute
Step (4): Compute MM estimator as in (7) for some ρ-function ρ1: Let g=0 and compute 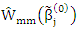 and let
and let 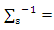
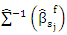
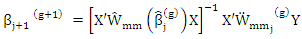 Step (5): If either m equal the maximum number of iterationsor
Step (5): If either m equal the maximum number of iterationsor 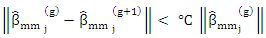 where
where 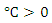 is affixed small constant, then
is affixed small constant, then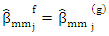 breakElse Compute
breakElse Compute 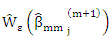 and put g←g+1Step (6): Select
and put g←g+1Step (6): Select 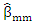 which active
which active 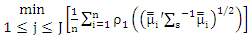 The J random subsample for initial candidates
The J random subsample for initial candidates 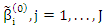 ware chosen as set for OLS estimators. To avoid ill condition, we take J by large size.Algorithm (2)In this algorithm, we compute MM ridge estimators for SUR model
ware chosen as set for OLS estimators. To avoid ill condition, we take J by large size.Algorithm (2)In this algorithm, we compute MM ridge estimators for SUR model 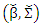 by develop (Maronna R, 2011), (Tharmaratnam et al., 2008) and (Al-hosany et al., 2011) algorithms.We drawing the algorithm (2) by the following steps:Step (1): We use the steps (1,2,3) in algorithm (1).Step (2): Compute MM ridge estimator as in (11) for some ρ-function ρ1. Let g = 0 and compute
by develop (Maronna R, 2011), (Tharmaratnam et al., 2008) and (Al-hosany et al., 2011) algorithms.We drawing the algorithm (2) by the following steps:Step (1): We use the steps (1,2,3) in algorithm (1).Step (2): Compute MM ridge estimator as in (11) for some ρ-function ρ1. Let g = 0 and compute 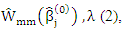
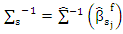 and let
and let 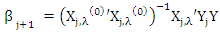 Step (3): If either m equal the maximum number of iterationsOr
Step (3): If either m equal the maximum number of iterationsOr 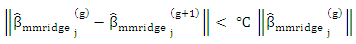 where
where 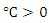 is affixed small constant, then
is affixed small constant, then 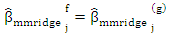 breakElse Compute
breakElse Compute 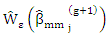 and put g←g+1Step (4): Select
and put g←g+1Step (4): Select 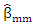 active
active 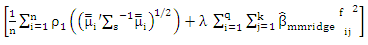
6. Result for Simulation
We summarize the simulation results in tables (1, 2). These tables shows the median ASE for GLS,S, MM and MM ridge estimators for SUR model under the study factors. When analysis the result of simulation study, we can say that, the GLS estimators, in all case, works better than anther estimators when the percentages of outliers close to zero percentage. Although S estimator has clear advantage when percentages of outliers reach to 20% and 45%, but the MM estimators have more efficiency. When the number of observations were increasing, we note improvement in the work of all the estimators. On other hand, when the number of equations increase, all estimators going to be less efficient. works good when the percentage of outliers and correlation between explanatory variables increases. The MM estimators and MM ridge estimators works good when the percentage of outliers and correlation between explanatory variables increases. Nevertheless, MM ridge estimators get more efficient than MM estimators.Table (1). Median ASE for GLS, S, MM and MM ridge estimators for SUR model, (percentages of outliers(ν) = 20%
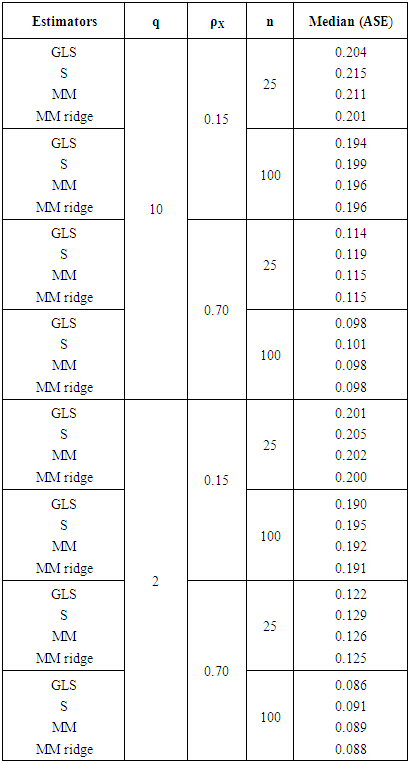 |
| |
|
Table (2). Median ASE for (GLS), S, MM and MM ridge estimator for SUR model, (percentages of outliers(ν) = 45%
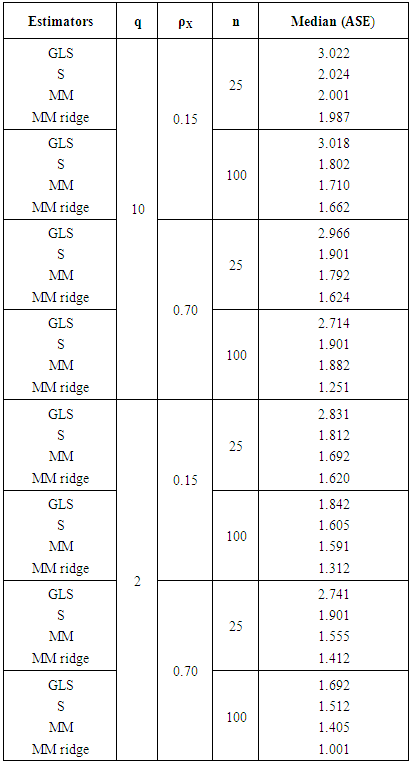 |
| |
|
7. Conclusions
To reach the best estimator for the SUR model which have advantages of the robust parameter estimation, we compare between the robust and nonrobust estimators. To attain the robust high level break down point, we used S, MM and MM ridge estimator for SUR model. The MM ridge estimators avoids the multicollinearity problem, which accompany the outliers. The median average squared error [Median (ASE)] was used for trade-off between estimators. The result of simulation show that, when the percentage of outlier and correlation between explanatory are increasing, the MM and MM ridge estimators are the best estimators between the robust and nonrobust estimators under the all factors of study.
References
| [1] | Berrendero J., Mendez B. and Tyler D. (2007), “On the maximum bias functions of MM-estimates and constrained M-estimates of regression”, The Annals of Statistics, Vol.35, No. 1. |
| [2] | Bilodeau M. and Duchesne P. (2000), "Robust estimation of the SUR model", The Canadian Journal of Statistics, Vol. 28. |
| [3] | Copt S. and Heritier S. (2006), “Robust MM-estimation and inference in mixed linear models”, Biometrics, Vo.1. |
| [4] | El- Houssainy A., Sayed M., Alaa A., Naglaa A. and Tarek m. (2011), "Robust cross validation in SUR ridge etimators and SUR robust ridge estimators", Journal of statistic theory and application, Vol. 10, No.1. |
| [5] | Garcia M., Martinez E. and Yohai V. (2006), “Robust estimation for the multivariate linear model based on a τ –scale”, Journal of Multivariate Analysis, Vo. 97. |
| [6] | Hendrik P. and Lopuha Äa, H. P. (1992), “Highly efficient estimators of multivariate location with high breakdown Point’, The Annals of Statistics, Vol. 20, No. 1. |
| [7] | Jose R., Beatriz V. and David E. (2007), “On the maximum bias functions of MM-estimates and constrained M-estimates of regression”, The Annals of statistics, Vo. 35. |
| [8] | Koenker, R. and Portnoy, S. (1990), "M-estimation of multivariate regressions". Journal of American Statistics Association, Vol. 63. |
| [9] | Kudraszow N. and Moronna R. (2011), Estimates of MM type for the multivariate linear model, Journal of Multivariate Analysis, Vol. 102, No. 9. |
| [10] | Lopuha Äa H. (1989), "On the relation between S-estimators and M-estimators of multivariate location and covariance" The Annals of Statistics, Vol.17. |
| [11] | LopuhaÄa H. (1992), “Highly efficient estimators of multivariate location with high breakdown point", Annals of Statistics, Vo,20. |
| [12] | Maronna R. and Zamar R. (2002), “Robust estimates of location and dispersion for high-dimensional datasets”, Technometrics, Vo.44, No.4. |
| [13] | Maronna R. (2011) “Robust ridge regression for high-dimensional Data”, Technometrics, Vo.53, No.1. |
| [14] | Meriam S., Said M., Iqbal M. and Ismail B. (2012),” Weight ridge MM-estimator in robust ridge regression with Multicollinearity”, Mathmatical Models and Methods in Modem Science Conference, 14th. |
| [15] | Moawad E. and Abd E. (2011), ”Estimation methods for multicollinearity problem combined with high leverage data points”, Journal of Mathematics and Statistics, Vo.7, No. 2. |
| [16] | Roelandt E., Van S. and Croux C. (2009). Multivariate Generalized S estimators, Journal of Multivariate Analysis, Vo.100, No.5. |
| [17] | Rousseeuw, P. and Leroy. A (1987), “Robust regression and outlier detection”, John Wiley, New York. |
| [18] | Ruppert D. (1992). "Computing S estimators for regression and multivariate location/dispersion", Journal of computational and graphical statistics, Vol. 32. |
| [19] | Salibian B. and Yohai V. (2008) "High breakdown point robust regression with censored data", The Annals of Statistics, vol. 36. |
| [20] | Srivastava V. and Giles D. (1987), “Seemingly unrelated regression equations Models: Estimation and Inference”, New York: Marcel Dekker. |
| [21] | Tharmaratnam, K. and Claeskens G. (2008). "S-Estimation for Penalized Regression Splines", Comput. Statist., Vol.30. |
| [22] | Yohai V. (1987), "High breakdown point and high efficiency robust estimates for regression," Annals of Statistics, Vo. 15. |
| [23] | Zellner A. (1962), “An efficient method of estimating seemingly unrelated regressions and tests for aggregation bias”, Journal of American Statistics Association, Vol. 57. |



 for multivariate regression which have excellent robustness and high efficiency under normality of error. (Roelandt etal., 2009) extract generalized S estimates for multivariate regression which consider high breakdown estimation when analysis the independent component. The MM estimators for linear regression model was introduced by (Yohai, 1987)), which begin at the first with a highly initial robust regression estimator like S estimators which depend on a loss function
for multivariate regression which have excellent robustness and high efficiency under normality of error. (Roelandt etal., 2009) extract generalized S estimates for multivariate regression which consider high breakdown estimation when analysis the independent component. The MM estimators for linear regression model was introduced by (Yohai, 1987)), which begin at the first with a highly initial robust regression estimator like S estimators which depend on a loss function 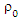 and then used this initial estimator to obtain M estimator with other loss function
and then used this initial estimator to obtain M estimator with other loss function 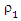 . This estimator has two advantage, the high asymptotic efficiency for normality error and high breakdown point reach to 50%. The study of (Berrendero etal., 2007) show that, the asymptotic bias for mm estimator is lower than the τ estimators when we contaminations error lower than 0.20 and the MM estimator has best lower maximum bias curve than other robust estimators. (Salibian etal., 2006) show that, the breakdown point of MM-estimator in finite-sample is equal to or greater than initial S-estimator. The MM estimators begin at the first with a highly initial robust regression estimator like S estimators which depend on a loss function
. This estimator has two advantage, the high asymptotic efficiency for normality error and high breakdown point reach to 50%. The study of (Berrendero etal., 2007) show that, the asymptotic bias for mm estimator is lower than the τ estimators when we contaminations error lower than 0.20 and the MM estimator has best lower maximum bias curve than other robust estimators. (Salibian etal., 2006) show that, the breakdown point of MM-estimator in finite-sample is equal to or greater than initial S-estimator. The MM estimators begin at the first with a highly initial robust regression estimator like S estimators which depend on a loss function 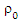 and then used this initial estimator to obtain M estimator with other loss function
and then used this initial estimator to obtain M estimator with other loss function 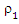 . (Kudraszow, 2011) suggested MM estimator for multivariate linear model and study the consistency and asymptotic normality with elliptical distribution for error. On other hand, frequently, outliers appear with degree of multicollinearity. The ridge method solved multicollinearity problem has been discussed by (Hoerl etal., 1970). This method is a way of proceeding in solving the problem by adding specific information to remove the ill-condition. The SUR model possibly is under the influence of multicollinarity. (Srivastava etal., 1987) suggested general ridge estimator to remove the ill-condition in SUR model (Alkhamisi. etal, 2006) developed ridge estimators of the SUR model, when the data are transformed in a canonical form. The critical point in ridge estimate is how to choose the shrink parameter. So, (Firinguetti, 1997), (Kibria etal., 2003) and (Alkhamisi. etal, 2006) suggested non robust Criteria to choice the shrink parameter in ridge estimator for SUR model. These formulas assume choosing ridge parameter when data without outliers. (Jung, 2009) proposed robust cross validation in ridge regression when data are within outliers. (El-hosany etal., 2011) used robust Cross Validation Criteria to choice shrink parameter in SUR model.In fact, frequently, outliers appear with degree of multicollinearity. Therefore, (El-hosany etal., 2011) mingle between ridge estimator and S- estimator to get robust ridge estimator. (Maronna, 2011), (Moawad etal., 2011) and (Mariam. etal., 2012) have developed MM-estimators to deal with leverage point and absorption problem of multicollinearity. This estimators builded by combined between ridge regression and mm-type to reach to mm ridge estimators. There is no study use the MM estimator in the SUR model. So, we suggests, MM and MM ridge estimator for SUR model to deal with bad high leverage points and the multicollinearity problem associated with it. In MM ridge estimator, we develop robust Cross Validation Criteria, to choice shrink parameter, depended on MM estimator. This paper organized as follows: The SUR model and estimators defined in Section two. In section three, we study the asymptotic properties of MM and MM ridge estimators in SUR model while section four will be devoted to make the simulation study. In section five, we develop algorithm to compute MM and MM ridge estimator for SUR model.
. (Kudraszow, 2011) suggested MM estimator for multivariate linear model and study the consistency and asymptotic normality with elliptical distribution for error. On other hand, frequently, outliers appear with degree of multicollinearity. The ridge method solved multicollinearity problem has been discussed by (Hoerl etal., 1970). This method is a way of proceeding in solving the problem by adding specific information to remove the ill-condition. The SUR model possibly is under the influence of multicollinarity. (Srivastava etal., 1987) suggested general ridge estimator to remove the ill-condition in SUR model (Alkhamisi. etal, 2006) developed ridge estimators of the SUR model, when the data are transformed in a canonical form. The critical point in ridge estimate is how to choose the shrink parameter. So, (Firinguetti, 1997), (Kibria etal., 2003) and (Alkhamisi. etal, 2006) suggested non robust Criteria to choice the shrink parameter in ridge estimator for SUR model. These formulas assume choosing ridge parameter when data without outliers. (Jung, 2009) proposed robust cross validation in ridge regression when data are within outliers. (El-hosany etal., 2011) used robust Cross Validation Criteria to choice shrink parameter in SUR model.In fact, frequently, outliers appear with degree of multicollinearity. Therefore, (El-hosany etal., 2011) mingle between ridge estimator and S- estimator to get robust ridge estimator. (Maronna, 2011), (Moawad etal., 2011) and (Mariam. etal., 2012) have developed MM-estimators to deal with leverage point and absorption problem of multicollinearity. This estimators builded by combined between ridge regression and mm-type to reach to mm ridge estimators. There is no study use the MM estimator in the SUR model. So, we suggests, MM and MM ridge estimator for SUR model to deal with bad high leverage points and the multicollinearity problem associated with it. In MM ridge estimator, we develop robust Cross Validation Criteria, to choice shrink parameter, depended on MM estimator. This paper organized as follows: The SUR model and estimators defined in Section two. In section three, we study the asymptotic properties of MM and MM ridge estimators in SUR model while section four will be devoted to make the simulation study. In section five, we develop algorithm to compute MM and MM ridge estimator for SUR model.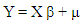
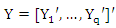 is a nq × 1 vector of dependant variable in q equation,
is a nq × 1 vector of dependant variable in q equation, 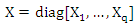 is a nq×kq matrix of independent variable and
is a nq×kq matrix of independent variable and 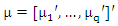 is a nq × 1 vector of random error in q equation. Suppose
is a nq × 1 vector of random error in q equation. Suppose 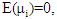
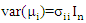 for all i=1,2,…q and
for all i=1,2,…q and 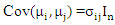 for all i,j=1,2,…q. We can right the SUR model in the multivariate form
for all i,j=1,2,…q. We can right the SUR model in the multivariate form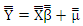
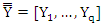 is a matrix of n q observations with
is a matrix of n q observations with 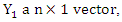
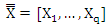 , is a
, is a 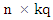 matrix,
matrix, 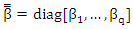 is a kq×q matrix of coefficients. and
is a kq×q matrix of coefficients. and 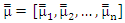 is a nq matrix of residual with
is a nq matrix of residual with 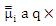
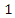 vector. Let
vector. Let 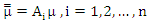 where
where 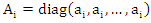 is a
is a 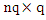 matrix and
matrix and 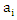 is vector contains one at position i and zero elsewhere. (Srivastava and Giles, 1987) suggested the GLS estimator for SUR model
is vector contains one at position i and zero elsewhere. (Srivastava and Giles, 1987) suggested the GLS estimator for SUR model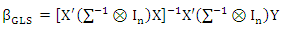
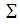 is q×q variance covariance matrix for error between equations. The GLS estimator calculate by use
is q×q variance covariance matrix for error between equations. The GLS estimator calculate by use 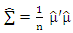 as consistent estimator for
as consistent estimator for 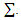 (Bilodeau etal, 2000) introduce S estimator to deal with outliers for SUR model. This estimator used the Huber function at the form
(Bilodeau etal, 2000) introduce S estimator to deal with outliers for SUR model. This estimator used the Huber function at the form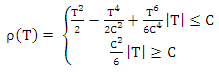
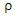 is symmetric, continuous, differentiable and for
is symmetric, continuous, differentiable and for 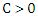 it is strictly increasing on [0; c], constant on [c,∞] and ρ(0)= 0. The percentage of breakdown point depend on C. (Ruppert, 1992) show that, when choice C=1.5476 the of breakdown point reach to 50%. The S estimator for SUR model minimize
it is strictly increasing on [0; c], constant on [c,∞] and ρ(0)= 0. The percentage of breakdown point depend on C. (Ruppert, 1992) show that, when choice C=1.5476 the of breakdown point reach to 50%. The S estimator for SUR model minimize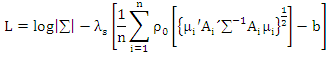 where
where 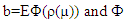 is the standard normal distribution. The S estimator satisfy the following equation
is the standard normal distribution. The S estimator satisfy the following equation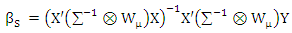
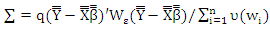
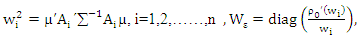
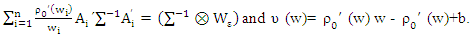 Lemma (1): Let the
Lemma (1): Let the 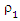 and
and 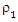 have symmetric, continuous, differentiable, for
have symmetric, continuous, differentiable, for 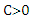 it is strictly increasing on [0; c], constant on [c,∞] and ρ(0)= 0. In adding, the function ρo and ρ1 achieve ρ1 (µ) ≤ ρo (µ) and Sup ρ1 (µ) = Sup ρ0 (µ). We use Huber function at the form (4). In the SUR model in (1). We can extracted the MM-estimator for SUR model (new) by
it is strictly increasing on [0; c], constant on [c,∞] and ρ(0)= 0. In adding, the function ρo and ρ1 achieve ρ1 (µ) ≤ ρo (µ) and Sup ρ1 (µ) = Sup ρ0 (µ). We use Huber function at the form (4). In the SUR model in (1). We can extracted the MM-estimator for SUR model (new) by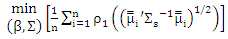
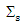 estimated by
estimated by 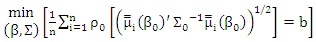
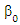 and
and 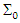 are initial estimators.Then the MM-estimator for SUR model satisfy the following equations
are initial estimators.Then the MM-estimator for SUR model satisfy the following equations 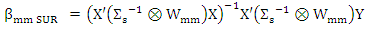
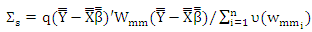
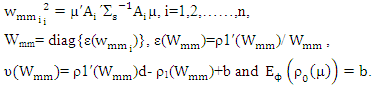 Proof of lemma (1)If we differentiate (7) with respect to β and equalize the result to zero then
Proof of lemma (1)If we differentiate (7) with respect to β and equalize the result to zero then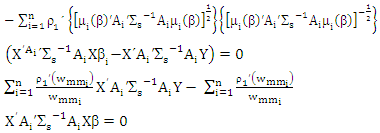 Where
Where 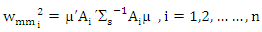 Then
Then 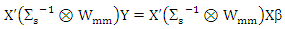 Where
Where 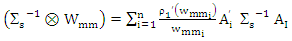 and
and 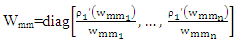 Then complete the proof.Lemma (2) If
Then complete the proof.Lemma (2) If 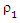 and
and 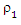 satisfy the condition in lemma (1), then we extract MM ridge estimator for SUR model (new) by
satisfy the condition in lemma (1), then we extract MM ridge estimator for SUR model (new) by 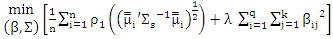
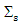 estimated by (8) and
estimated by (8) and 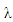 is ridge parameter. The MM ridge estimator for SUR model (new) in (1) can be written as
is ridge parameter. The MM ridge estimator for SUR model (new) in (1) can be written as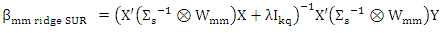
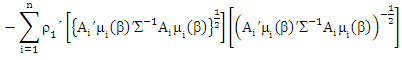
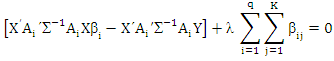
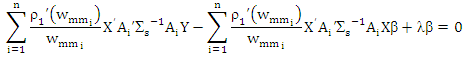 Then complete the proof.
Then complete the proof.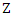 observe,
observe, 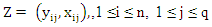 which independent random vectors distributed as pq-variate normal distribution
which independent random vectors distributed as pq-variate normal distribution 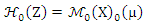 with mean μ= Zβ and variance ∑s, where
with mean μ= Zβ and variance ∑s, where 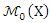 is distribution of X and
is distribution of X and 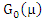 is distribution of µ.Then
is distribution of µ.Then
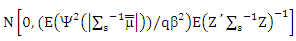 Where
Where 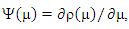
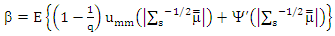 Proof of lemma (3):We use the proof for the Theorem (4-1) in (Yohai, 1987) and the asymptotical properties for S-estimator for SUR model in (Bilodeau etal, 2000) to access the prove. The MM-estimator of
Proof of lemma (3):We use the proof for the Theorem (4-1) in (Yohai, 1987) and the asymptotical properties for S-estimator for SUR model in (Bilodeau etal, 2000) to access the prove. The MM-estimator of 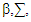 in SUR model, can be defined as a solution of M-type equation, then the anther form for equations (8) and (9) are
in SUR model, can be defined as a solution of M-type equation, then the anther form for equations (8) and (9) are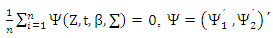
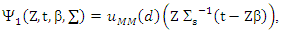
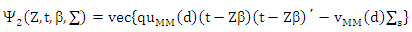 By using Mean Value Theorem (MVT),
By using Mean Value Theorem (MVT),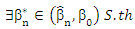
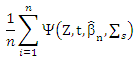
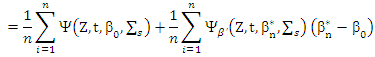 For (14)
For (14) 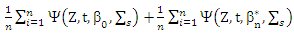
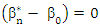 Then
Then 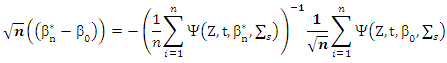 For uniform laws of large numbers (ULLN)
For uniform laws of large numbers (ULLN)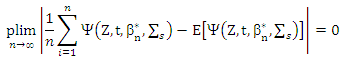
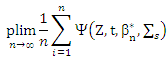
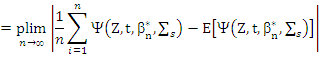
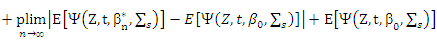 By central limit theorem (CLT), we get
By central limit theorem (CLT), we get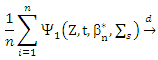
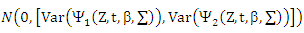 And then
And then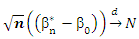
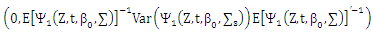 Under the assumption u elliptical. We study the asymptotic variance for
Under the assumption u elliptical. We study the asymptotic variance for 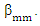 Hence
Hence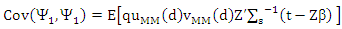
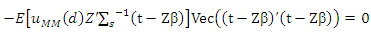 Let:
Let: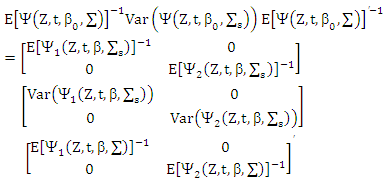 while
while 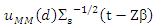 is spherical then
is spherical then 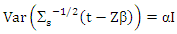
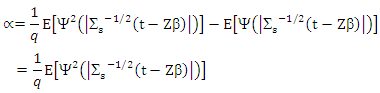 and then
and then 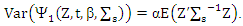 Extension for Lemma (5-1) (Lopuhaa, 1989). We get
Extension for Lemma (5-1) (Lopuhaa, 1989). We get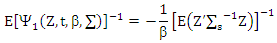 Where
Where 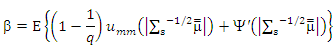 Then
Then 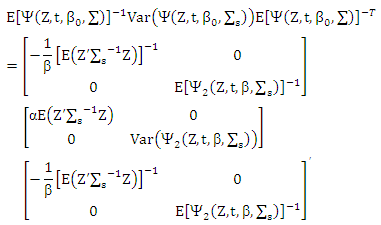 Then
Then 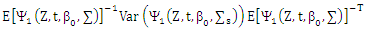
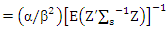 Then completes the proof.Lemma (4):Consider the same condition in proposition (3-1) and
Then completes the proof.Lemma (4):Consider the same condition in proposition (3-1) and 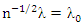 then
then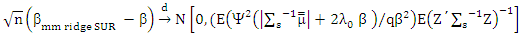
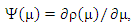
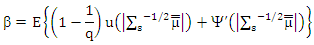 and then
and then 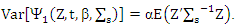 Following by the proof for lemma (3) then completes the proof.
Following by the proof for lemma (3) then completes the proof.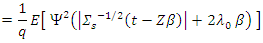 Where
Where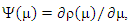
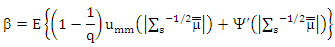 and
and 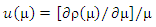 Proof of lemma (4):The MM ridge estimator of β,∑, in SUR model, can be defined as a solution of M-type equation, then the anther form for equations (9) and (12) are
Proof of lemma (4):The MM ridge estimator of β,∑, in SUR model, can be defined as a solution of M-type equation, then the anther form for equations (9) and (12) are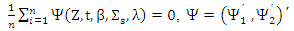
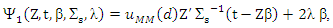
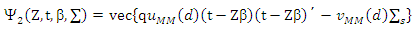 By using (MVT, (ULLN) and (CLT)) theorem in proofs for proportion (3-2). In adding, consider the condition
By using (MVT, (ULLN) and (CLT)) theorem in proofs for proportion (3-2). In adding, consider the condition 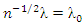 then
then 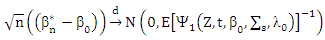
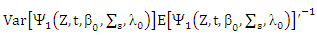 Under the assumption u elliptical. We study the asymptotic variance for
Under the assumption u elliptical. We study the asymptotic variance for 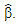 Hence
Hence 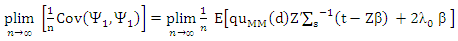 Let:
Let: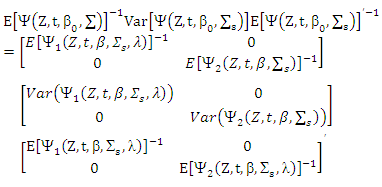 While
While 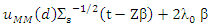 is spherical then
is spherical then 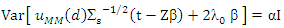 Where
Where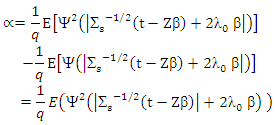 and then
and then 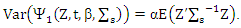 Following by the proof for lemma (3) then completes the proof.
Following by the proof for lemma (3) then completes the proof.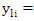
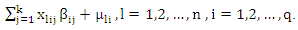 Where
Where 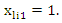 In this simulation, we set the initial value for β= [1,2,3] for k=3. The explanatory variables are generated by multivariate normal distribution MNNk=3 (0,∑x) where diag(∑x)=1, off-diag(∑x)= ρX= 0.15 for low interdependency and ρx= 0.70 for high interdependency. Where ρx is correlation between explanatory variables. We chose two sample size 25 for small sample and 100 for large sample. The specific error in equations μi, i=1,2,…..,n, we generated by MVNk=3 (0, ∑ε), ∑ε the variance covariance matrix of errors, diag(∑ε)= 1, off-diag(∑ε)= ρε= 0.15. To investigate the robustness of the estimators against outliers, we chosen different percentages of outliers ( 20%, 45%). We choose shrink parameter in (12) by minimize the new robust Cross Validation (CVMM) criterion which avoided outliers. This criterion depend on MM estimators and takes the form
In this simulation, we set the initial value for β= [1,2,3] for k=3. The explanatory variables are generated by multivariate normal distribution MNNk=3 (0,∑x) where diag(∑x)=1, off-diag(∑x)= ρX= 0.15 for low interdependency and ρx= 0.70 for high interdependency. Where ρx is correlation between explanatory variables. We chose two sample size 25 for small sample and 100 for large sample. The specific error in equations μi, i=1,2,…..,n, we generated by MVNk=3 (0, ∑ε), ∑ε the variance covariance matrix of errors, diag(∑ε)= 1, off-diag(∑ε)= ρε= 0.15. To investigate the robustness of the estimators against outliers, we chosen different percentages of outliers ( 20%, 45%). We choose shrink parameter in (12) by minimize the new robust Cross Validation (CVMM) criterion which avoided outliers. This criterion depend on MM estimators and takes the form 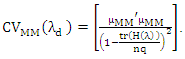 Where
Where 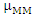 is a residual depend on MM estimators and
is a residual depend on MM estimators and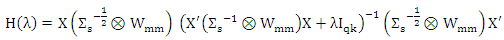 We measure the goodness of fit of estimated model for β by use the median average squared error [Median(ASE_j)] where ASE_j is defined by
We measure the goodness of fit of estimated model for β by use the median average squared error [Median(ASE_j)] where ASE_j is defined by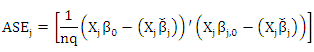 where j=1,2,……N. Where
where j=1,2,……N. Where 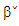 is MM estimator for β and N is a number of iteration. We run N=1,2,…, 500 replications by using software MATHCAD.
is MM estimator for β and N is a number of iteration. We run N=1,2,…, 500 replications by using software MATHCAD.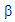 and
and 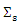 is initial estimate for
is initial estimate for 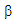 and
and 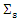 respectively, then iterative solve for (9) is
respectively, then iterative solve for (9) is 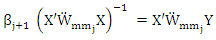
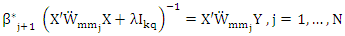
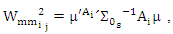
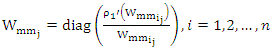
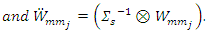 The equation (17) is a weight version for ridge estimator. This equation is rewrite as normal equations
The equation (17) is a weight version for ridge estimator. This equation is rewrite as normal equations 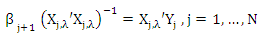
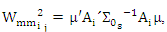
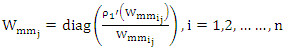 and
and 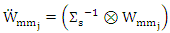 The equation (14) is a weight version for ridge estimator. This equation is rewrite as normal equations
The equation (14) is a weight version for ridge estimator. This equation is rewrite as normal equations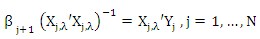
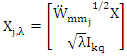 and
and 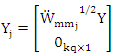 Algorithm (1)In this algorithm, we compute MM estimators for SUR model
Algorithm (1)In this algorithm, we compute MM estimators for SUR model 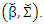 by developed the algorithms for (Tharmaratnam et al., 2008) and (Al-hosany et al., 2011) We drawing the algorithm (1) by the following steps:Step (1): Let
by developed the algorithms for (Tharmaratnam et al., 2008) and (Al-hosany et al., 2011) We drawing the algorithm (1) by the following steps:Step (1): Let 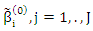 is initial candidates estimate for β.Step (2): Design the variable
is initial candidates estimate for β.Step (2): Design the variable 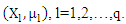 For each
For each 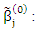 a. Compute
a. Compute 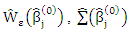 b. Compute S estimators as in (8) for some ρ-function ρ0 by set m=0, and get the following steps:i. Let
b. Compute S estimators as in (8) for some ρ-function ρ0 by set m=0, and get the following steps:i. Let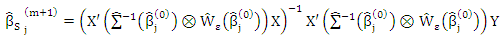 ii. If either m equal the maximum number of iterationsor
ii. If either m equal the maximum number of iterationsor 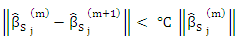 where
where 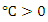 is affixed smalliii. constant, then
is affixed smalliii. constant, then 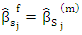 go to step (2)iv. Else Compute
go to step (2)iv. Else Compute 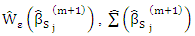 , and put m←m+1Step (3): Select
, and put m←m+1Step (3): Select 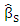 which active
which active 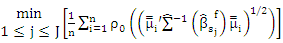 Step (4): Compute MM estimator as in (7) for some ρ-function ρ1: Let g=0 and compute
Step (4): Compute MM estimator as in (7) for some ρ-function ρ1: Let g=0 and compute 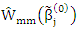 and let
and let 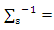
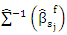
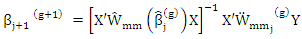 Step (5): If either m equal the maximum number of iterationsor
Step (5): If either m equal the maximum number of iterationsor 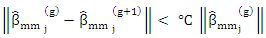 where
where 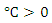 is affixed small constant, then
is affixed small constant, then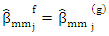 breakElse Compute
breakElse Compute 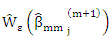 and put g←g+1Step (6): Select
and put g←g+1Step (6): Select 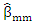 which active
which active 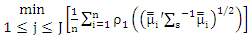 The J random subsample for initial candidates
The J random subsample for initial candidates 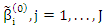 ware chosen as set for OLS estimators. To avoid ill condition, we take J by large size.Algorithm (2)In this algorithm, we compute MM ridge estimators for SUR model
ware chosen as set for OLS estimators. To avoid ill condition, we take J by large size.Algorithm (2)In this algorithm, we compute MM ridge estimators for SUR model 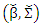 by develop (Maronna R, 2011), (Tharmaratnam et al., 2008) and (Al-hosany et al., 2011) algorithms.We drawing the algorithm (2) by the following steps:Step (1): We use the steps (1,2,3) in algorithm (1).Step (2): Compute MM ridge estimator as in (11) for some ρ-function ρ1. Let g = 0 and compute
by develop (Maronna R, 2011), (Tharmaratnam et al., 2008) and (Al-hosany et al., 2011) algorithms.We drawing the algorithm (2) by the following steps:Step (1): We use the steps (1,2,3) in algorithm (1).Step (2): Compute MM ridge estimator as in (11) for some ρ-function ρ1. Let g = 0 and compute 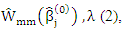
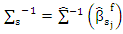 and let
and let 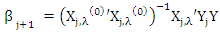 Step (3): If either m equal the maximum number of iterationsOr
Step (3): If either m equal the maximum number of iterationsOr 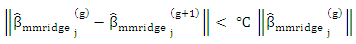 where
where 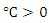 is affixed small constant, then
is affixed small constant, then 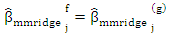 breakElse Compute
breakElse Compute 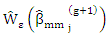 and put g←g+1Step (4): Select
and put g←g+1Step (4): Select 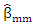 active
active 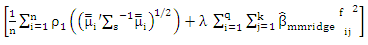
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
