-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Statistics and Applications
p-ISSN: 2168-5193 e-ISSN: 2168-5215
2016; 6(6): 376-385
doi:10.5923/j.statistics.20160606.06

A Size-Biased Poisson-Amarendra Distribution and Its Applications
Rama Shanker1, Hagos Fesshaye2
1Department of Statistics, Eritrea Institute of Technology, Asmara, Eritrea
2Department of Economics, College of Business and Economics, Halhale, Eritrea
Correspondence to: Rama Shanker, Department of Statistics, Eritrea Institute of Technology, Asmara, Eritrea.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper, a size-biased Poisson-Amarendra distribution (SBPAD) has been proposed by size-biasing the Poisson-Amarendra distribution (PAD) of Shanker (2016 b), a Poisson mixture of Amarendra distribution introduced by Shanker (2016 a). The first four moments (about origin) and the central moments (about mean) have been obtained and expressions for coefficient of variation (C.V), skewness, kurtosis and index of dispersion have been given. The estimation of its parameter has been discussed using maximum likelihood estimation and method of moments. Three examples of real data-sets have been presented to test the goodness of fit of SBPAD over size-biased Poisson distribution (SBPD), size-biased Poisson-Lindley distribution (SBPLD) and size-biased Poisson-Sujatha distribution (SBPSD).
Keywords: Amarendra distribution, Poisson-Amarendra distribution, Sujatha distribution, Poisson-Sujatha distribution, Size-biasing, Moments, Estimation of parameter, Goodness of fit
Cite this paper: Rama Shanker, Hagos Fesshaye, A Size-Biased Poisson-Amarendra Distribution and Its Applications, International Journal of Statistics and Applications, Vol. 6 No. 6, 2016, pp. 376-385. doi: 10.5923/j.statistics.20160606.06.
Article Outline
1. Introduction
- Size-biased distributions are a particular class of weighted distributions which arise naturally in practice when observations from a sample are recorded with probability proportional to some measure of unit size. In field applications, size-biased distributions can arise either because individuals are sampled with unequal probability by design or because of unequal detection probability. Size-biased distributions come into play when organisms occur in groups, and group size influences the probability of detection. Fisher (1934) firstly introduced these distributions to model ascertainment biases which were later formalized by Rao (1965) in a unifying theory for problems where the observations fall in non-experimental, non-replicated and non-random categories. Size-biased distributions have applications in environmental science, econometrics, social science, biomedical science, human demography, ecology, geology, forestry etc. Van Duesen (1986) has detailed study about the applications of size-biased distributions for fitting distributions of diameter at breast height (DBH) data arising from horizontal point sampling (HPS). Later, Lappi and Bailey (1987) have applied size-biased distributions to analyze HPS diameter increment data. The applications of size-biased distributions to the analysis of data relating to human population and ecology can be found in Patil and Rao (1977, 1978). A number of research have been done relating to size-biased distributions and their applications in different fields of knowledge by different researchers including Scheaffer (1972), Patil and Ord (1976), Singh and Maddala (1976), Patil (1981), McDonald (1984), Gove (2000, 2003), Correa and Wolfson (2007), Drummer and McDonald (1987), Ducey (2009), Alavi and Chinipardaz (2009), Ducey and Gove (2015), are some among others.Let a random variable
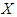 has probability distribution
has probability distribution 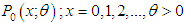 . If sample units are weighted or selected with probability proportional to
. If sample units are weighted or selected with probability proportional to 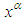 , then the corresponding size-biased distribution of order
, then the corresponding size-biased distribution of order 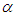 is given by its probability mass function
is given by its probability mass function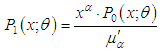 where
where 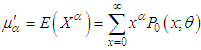 . When
. When 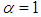 , the distribution is known as simple size-biased distribution and is applicable for size-biased sampling and for
, the distribution is known as simple size-biased distribution and is applicable for size-biased sampling and for  , the distribution is known as area-biased distribution and is applicable for area-biased sampling.
, the distribution is known as area-biased distribution and is applicable for area-biased sampling.2. Size-Biased Poisson-Amarendra Distribution (SBPAD)
- The Poisson-Amarendra distribution (PAD) having probability mass function (p.m.f.)
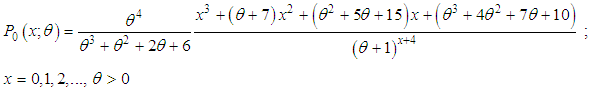 | (2.1) |
 follows Amarendra distribution introduced by Shanker (2016 a) with probability density function (p.d.f.)
follows Amarendra distribution introduced by Shanker (2016 a) with probability density function (p.d.f.)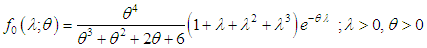 | (2.2) |
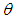 can be obtained as
can be obtained as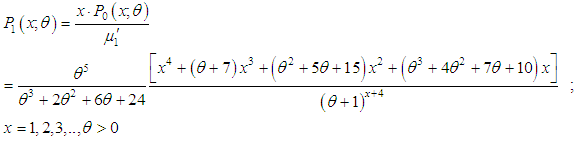 | (2.3) |
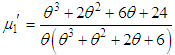 is the mean of the PAD with p.m.f. (2.1).Recall that the p.d.f. (2.3) of SBPAD can also be obtained from the size-biased Poisson distribution (SPBD) with p.m.f.
is the mean of the PAD with p.m.f. (2.1).Recall that the p.d.f. (2.3) of SBPAD can also be obtained from the size-biased Poisson distribution (SPBD) with p.m.f.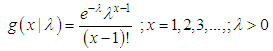 | (2.4) |
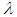 follows the size-biased Amarendra distribution (SBAD) with p.d.f.
follows the size-biased Amarendra distribution (SBAD) with p.d.f.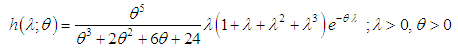 | (2.5) |
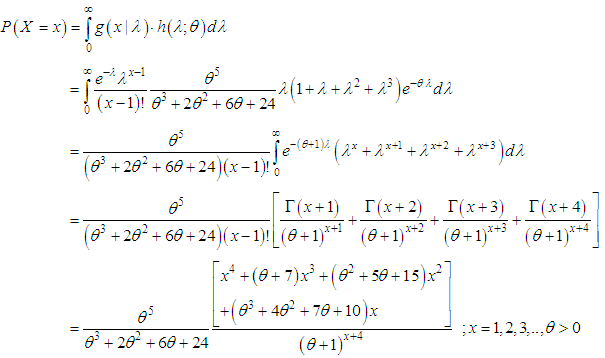 | (2.6) |
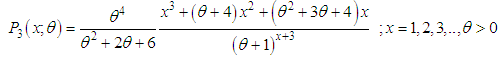 | (2.7) |
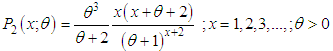 | (2.8) |
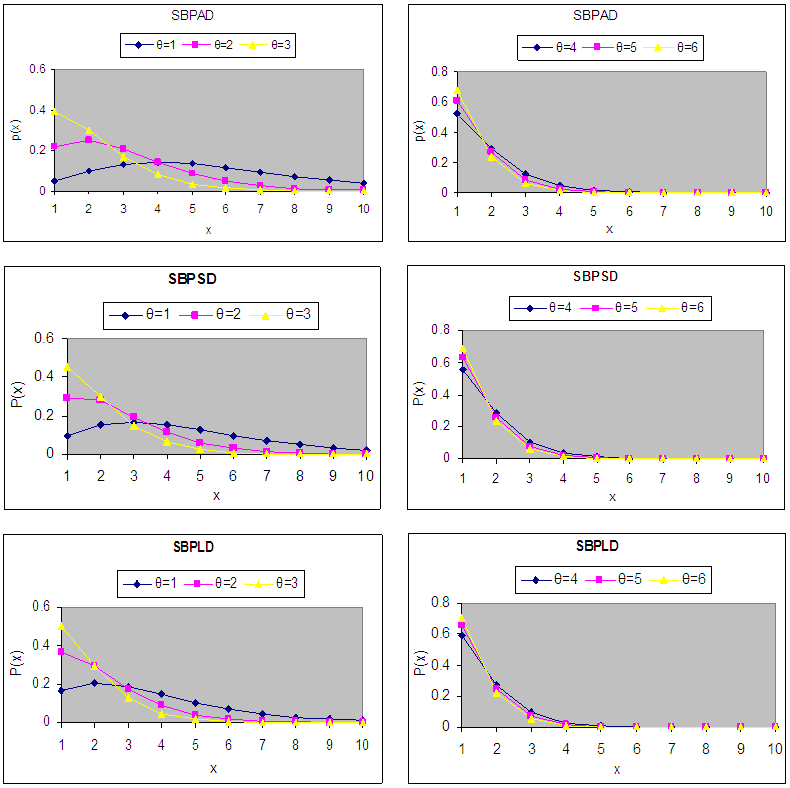 | Figure 1. Graphs of pmf of SBPAD, SBPSD and SBPLD for selected values of the parameter θ |
3. Moments and Associated Measures
- Using (2.6), the rth factorial moment about origin of the SBPAD (2.3) can be obtained as
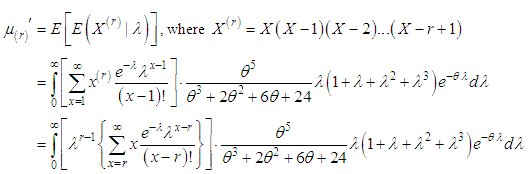 Taking
Taking 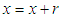 , we get
, we get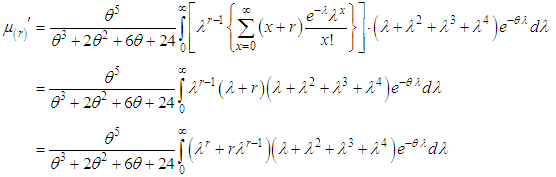 Using gamma integral and some small algebraic simplification, the rth factorial moment about origin of SBPAD (2.3) can be obtained as
Using gamma integral and some small algebraic simplification, the rth factorial moment about origin of SBPAD (2.3) can be obtained as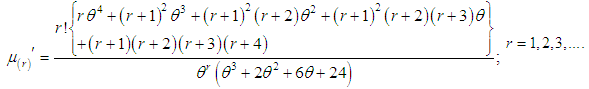 | (3.1) |
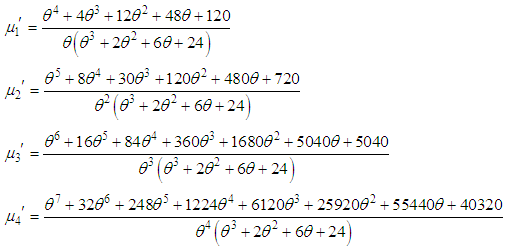 Now, using the relationship between central moments and the moments about origin, the central moments of the SBPAD (2.3) are thus obtained as
Now, using the relationship between central moments and the moments about origin, the central moments of the SBPAD (2.3) are thus obtained as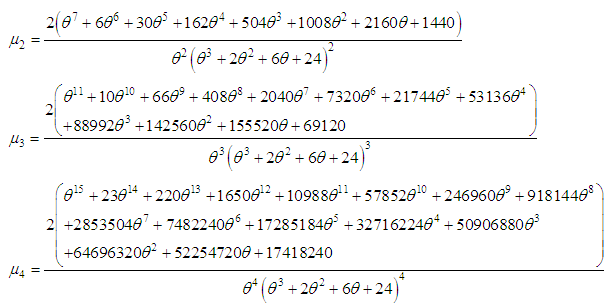 The coefficient of variation
The coefficient of variation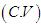 , coefficient of skewness
, coefficient of skewness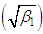 , coefficient of kurtosis
, coefficient of kurtosis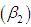 and index of dispersion
and index of dispersion 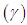 of the SBPAD (2.3) are finally obtained as
of the SBPAD (2.3) are finally obtained as  The conditions under which SBPAD, SBPSD and SBPLD are over-dispersed
The conditions under which SBPAD, SBPSD and SBPLD are over-dispersed 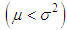 , equi-dispersed
, equi-dispersed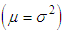 and under-dispersed
and under-dispersed 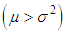 are presented in table 3.1.
are presented in table 3.1.
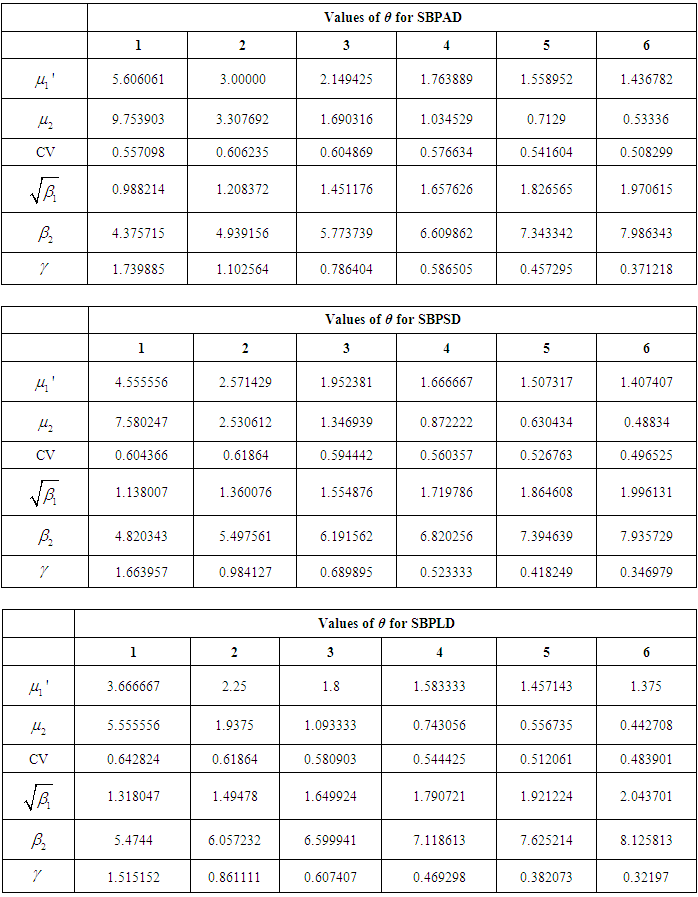
|
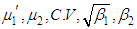 and
and 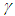 of SBPAD, SBPSD and SBPLD for varying values of their parameter
of SBPAD, SBPSD and SBPLD for varying values of their parameter 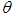 , the numerical values of these characteristics have been presented in table 3.2.
, the numerical values of these characteristics have been presented in table 3.2.
|
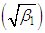 , coefficient of kurtosis
, coefficient of kurtosis 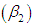 and index of dispersion
and index of dispersion 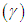 of SBPAD, SBPSD and SBPLD are shown in figure 2
of SBPAD, SBPSD and SBPLD are shown in figure 2 | Figure 2. Graphs of coefficient of variation (C.V), coefficient of skewness  , coefficient of kurtosis , coefficient of kurtosis  , and index of dispersion , and index of dispersion 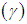 for SBPAD, SBPSD and SBPLD for selected values of their parameter θ for SBPAD, SBPSD and SBPLD for selected values of their parameter θ |
4. Unimodality and Increasing Failure Rate
- Using p.m.f. of SBPAD from (2.3), we have
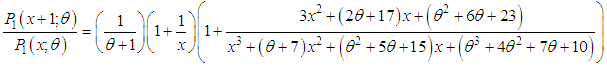 which is a deceasing function of x,
which is a deceasing function of x, 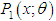 is log-concave. Therefore, SBPAD is unimodal, has an increasing failure rate (IFR), and hence increasing failure rate average (IFRA). It is new better than used in expectation (NBUE) and has decreasing mean residual life (DMRL). The definitions, concepts and interrelationship between these aging concepts have been discussed in Barlow and Proschan (1981).
is log-concave. Therefore, SBPAD is unimodal, has an increasing failure rate (IFR), and hence increasing failure rate average (IFRA). It is new better than used in expectation (NBUE) and has decreasing mean residual life (DMRL). The definitions, concepts and interrelationship between these aging concepts have been discussed in Barlow and Proschan (1981).5. Parameter Estimation
- 5.1. Maximum Likelihood Estimate (MLE): Let
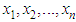 be a random sample of size n from the SBPAD (2.3) and let
be a random sample of size n from the SBPAD (2.3) and let 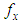 be the observed frequency in the sample corresponding to
be the observed frequency in the sample corresponding to 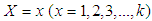 such that
such that 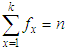 , where k is the largest observed value having non-zero frequency. The likelihood function Lof the SBPAD (2.3) is given by
, where k is the largest observed value having non-zero frequency. The likelihood function Lof the SBPAD (2.3) is given by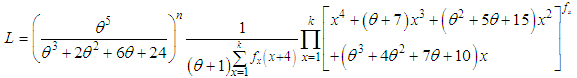 The log likelihood function can be obtained as
The log likelihood function can be obtained as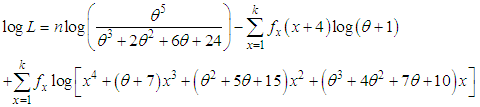 The first derivative of the log likelihood function is thus given by
The first derivative of the log likelihood function is thus given by 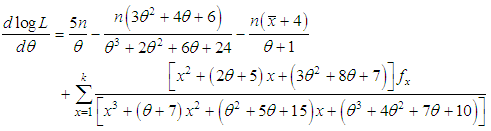 where
where 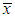 is the sample mean.The maximum likelihood estimate (MLE),
is the sample mean.The maximum likelihood estimate (MLE), 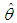 of
of 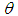 of SBPAD (2.3) is the solution of the equation
of SBPAD (2.3) is the solution of the equation 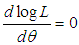 and is given by the solution of the following non-linear equation
and is given by the solution of the following non-linear equation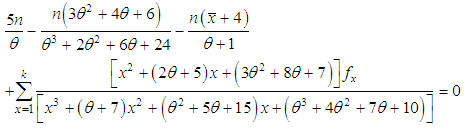 This non-linear equation can be solved by any numerical iteration methods such as Newton- Raphson method, Bisection method, Regula –Falsi method etc. In the present paper, Newton-Raphson method has been used to solve the above non-linear equation to find MLE of the parameter.5.2. Method of Moment Estimate (MOME): Equating the population mean to the corresponding sample mean, the method of moment estimate (MOME)
This non-linear equation can be solved by any numerical iteration methods such as Newton- Raphson method, Bisection method, Regula –Falsi method etc. In the present paper, Newton-Raphson method has been used to solve the above non-linear equation to find MLE of the parameter.5.2. Method of Moment Estimate (MOME): Equating the population mean to the corresponding sample mean, the method of moment estimate (MOME) 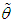 of
of 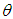 of SBPAD (2.3) is the solution of the following fourth degree polynomial equation in
of SBPAD (2.3) is the solution of the following fourth degree polynomial equation in 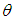
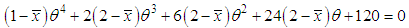 where
where 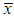 is the sample mean.
is the sample mean.6. Goodness of Fit
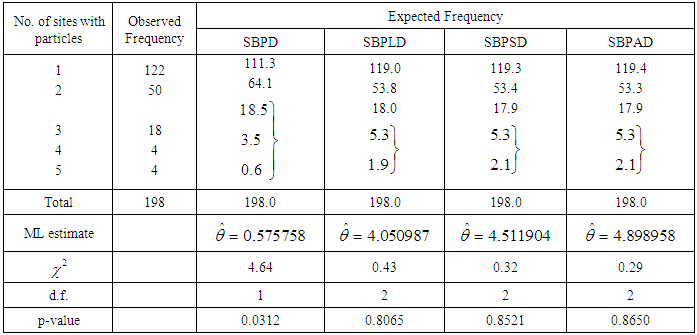
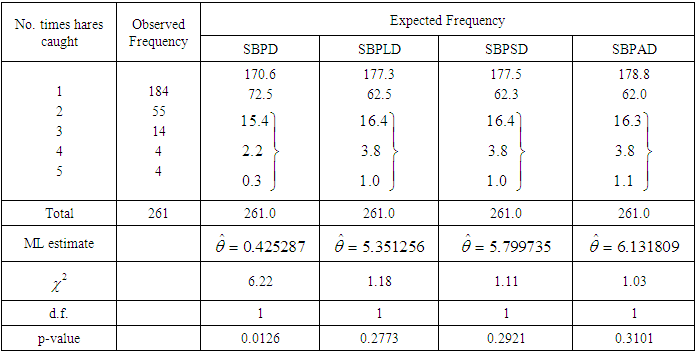
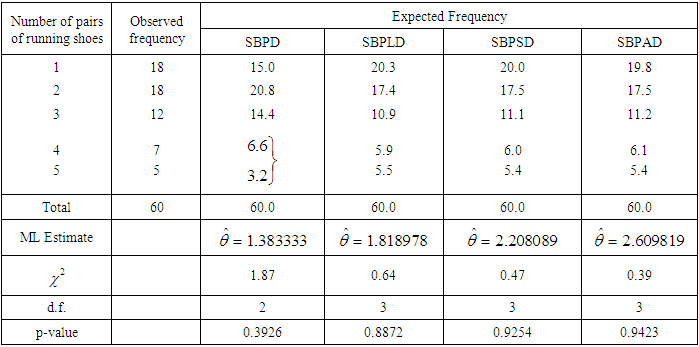
- In this section the goodness of fit of the SBPAD, SBPSD, SBPLD and SBPD have been presented for three count data- sets. The fitting of these distributions are based on maximum likelihood estimates of the parameter. The first data-set is immunogold assay data of Cullen et al. (1990) regarding the distribution of number of counts of sites with particles from immunogold assay data, the second data-set is animal abundance data of Keith and Meslow (1968) regarding the distribution of snowshoe hares captured over 7 days, and the third data-set is number of counts of pairs of running shoes owned by 60 members of an athletics club, reported by Simonoff (2003).
|
|
|
7. Concluding Remarks
- A size-biased Poisson mixture of size-biased Amarendra distribution named, “size-biased Poisson-Amarendra distribution (SBPAD)” has been proposed by size-biasing the Poisson-Amarendra distribution (PAD) of Shanker (2016 b). Its moments and other structural properties including coefficient of variation, skewness, kurtosis, index of dispersion, hazard rate and unimodality have been studied. The estimation of its parameter has been discussed using method of maximum likelihood and that of moments. Three examples of real data-sets have been presented to test the goodness of fit of SBPAD over the size-biased Poisson distribution (SBPD), the size-biased Poisson-Lindley distribution (SBPLD) and the size-biased Poisson -Sujatha distribution (SBPSD). The fit of SBPAD over SBPD, SBPLD, and SBPSD shows that SBPAD can be considered as an important distribution for modeling data which structurally excludes zero counts.
ACKNOWLEDGEMENTS
- The authors express their gratitude to the editor-in-chief and the anonymous reviewer for his constructive suggestions which improved the quality of the paper.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
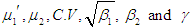 for SBPAD, SBPSD and SBPLD for selected values of the parameter θ
for SBPAD, SBPSD and SBPLD for selected values of the parameter θ