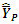Mukesh Kumar Sharma , Sarbjit Singh Brar , Harinder Kaur
Department of Statistics, Punjabi University, Patiala, India
Correspondence to: Harinder Kaur , Department of Statistics, Punjabi University, Patiala, India.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper, we first establish the new parametric relationship for population median 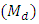 and then propose conventional consistent, ratio-type and product-type estimators of
and then propose conventional consistent, ratio-type and product-type estimators of 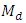 under different situations. The expression for their optimum biases and minimum mean square errors (MSE’s) are obtained, up to terms of order
under different situations. The expression for their optimum biases and minimum mean square errors (MSE’s) are obtained, up to terms of order 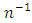 and compared with each other. Empirically, we have checked the authenticity of the relationship for
and compared with each other. Empirically, we have checked the authenticity of the relationship for 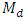 and also the gain in efficiencies of the proposed estimators with each other and existing ones are illustrated.
and also the gain in efficiencies of the proposed estimators with each other and existing ones are illustrated.
Keywords:
Auxiliary variable, Bias, Empirical relationship for mode, Estimation, Mean squared error, Median, Mode, Product estimator, Ratio estimator, Skewness
Cite this paper: Mukesh Kumar Sharma , Sarbjit Singh Brar , Harinder Kaur , Estimators of Population Median Using New Parametric Relationship, International Journal of Statistics and Applications, Vol. 6 No. 6, 2016, pp. 368-375. doi: 10.5923/j.statistics.20160606.05.
1. Introduction
In survey sampling, statisticians are often interested in dealing with variables that have highly skewed distributions such as consumptions, expenditure, income, etc. In such situations median is regarded as a more appropriate measure of location than mean. It has been well recognized that use of auxiliary variable information results in efficient estimators of population parameters. Initially, estimation of median without auxiliary variable was analyzed, after that some authors including Kuk and Mak (1989), Mak and Kuk (1993), Garcia and Cebrian (2001), Singh et al. (2006), Al and Cingi (2010) used the auxiliary information in median estimation. Singh and Solanki (2013), proposed the four estimators and a generalized class of estimators of population median 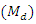 using known information of population median of the auxiliary variable. Empirically, they studied the 22 estimators. In this paper, we first establish the new parametric relationship for population median
using known information of population median of the auxiliary variable. Empirically, they studied the 22 estimators. In this paper, we first establish the new parametric relationship for population median 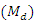 and propose three estimators of
and propose three estimators of 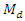 under different situations. This technique of estimation of population median is different from the existing one given by Kuk and Mak (1989), which is very simple and efficient. Up to terms of order
under different situations. This technique of estimation of population median is different from the existing one given by Kuk and Mak (1989), which is very simple and efficient. Up to terms of order 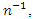 the optimum biases and minimum MSE’s of the proposed estimators are obtained and compared with each other. Empirically, we have done two studies, first to check the authenticity of the relationship for
the optimum biases and minimum MSE’s of the proposed estimators are obtained and compared with each other. Empirically, we have done two studies, first to check the authenticity of the relationship for 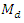 and to have the rough idea about the efficiencies of proposed estimators with each other. Secondly, to compare the efficiencies of the proposed estimators with existing ones as the techniques of estimation and parameters involved in their minimum MSE’s are different.
and to have the rough idea about the efficiencies of proposed estimators with each other. Secondly, to compare the efficiencies of the proposed estimators with existing ones as the techniques of estimation and parameters involved in their minimum MSE’s are different.
2. Notations and Results
Suppose a simple random sample of size 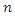 is drawn from a finite population of size
is drawn from a finite population of size 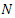 without replacement and observations on both study variables
without replacement and observations on both study variables 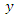 and auxiliary variable
and auxiliary variable 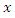 are taken. Let the values of variable
are taken. Let the values of variable 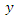 and
and 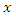 be denoted by
be denoted by 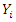 and
and 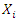 respectively on the
respectively on the 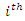 unit of the population
unit of the population 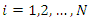 and the corresponding small letters
and the corresponding small letters 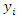 and
and 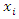 denote the sample values corresponding to the
denote the sample values corresponding to the 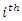 unit in the sample.Taking,
unit in the sample.Taking,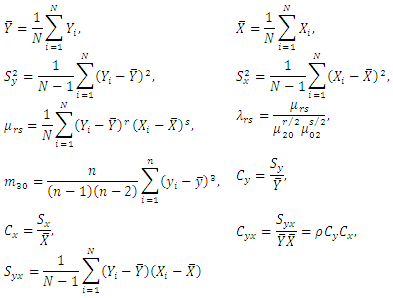 Obviously
Obviously Defining,
Defining,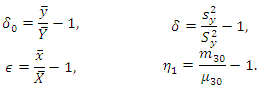 For the sake of simplicity, assume that
For the sake of simplicity, assume that 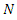 is large enough as compares to
is large enough as compares to 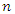 so that finite population correction (fpc) terms are ignored throughout.For the given SRSWOR, we have the following expectations,
so that finite population correction (fpc) terms are ignored throughout.For the given SRSWOR, we have the following expectations,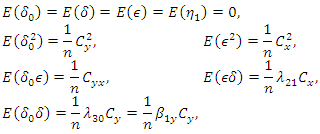 and up to terms of order
and up to terms of order 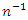
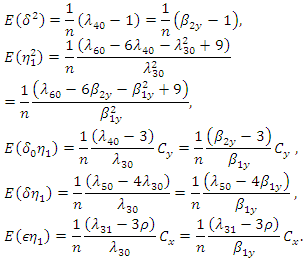
3. Proposed Estimators and Their Biases and MSE’s
Sharma et al. (2016) established the parametric relation for population mode as 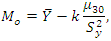 where
where 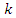 is unknown constant to be determined.Sharma et al. (2016) also proposed three estimators of
is unknown constant to be determined.Sharma et al. (2016) also proposed three estimators of 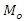 under the three different situations as
under the three different situations as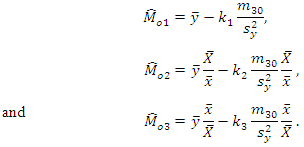 They determined the optimum value of
They determined the optimum value of 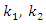 and
and 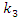 by minimizing the MSE’s of respective estimators as
by minimizing the MSE’s of respective estimators as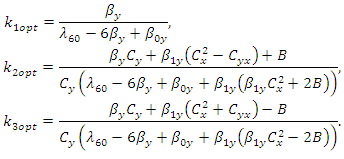 where,
where,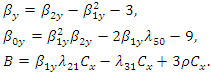 Note that
Note that 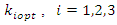 are further functions of unknown population parameters. Srivastava and Jhajj (1983) have shown that if we replace the parameters involved in the optimum value of the unknown constant by their consistent estimators then up to terms of order
are further functions of unknown population parameters. Srivastava and Jhajj (1983) have shown that if we replace the parameters involved in the optimum value of the unknown constant by their consistent estimators then up to terms of order 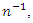 the MSE remains the same. Therefore, the presence of unknown parameters in the optimum values of the constants will not create any problem for practical use of the proposed estimators.Let
the MSE remains the same. Therefore, the presence of unknown parameters in the optimum values of the constants will not create any problem for practical use of the proposed estimators.Let 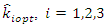 be the values when parameters are replaced by their consistent estimators in
be the values when parameters are replaced by their consistent estimators in 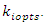 So then the estimators reduces to
So then the estimators reduces to 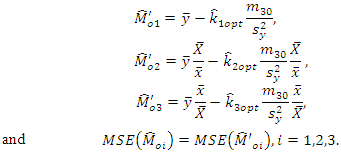 For moderately skewed distribution, Doodson (1917) suggested the empirical relationship as
For moderately skewed distribution, Doodson (1917) suggested the empirical relationship as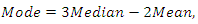 which is also known as Karl Pearson empirical relation between mean, median and mode.That implied
which is also known as Karl Pearson empirical relation between mean, median and mode.That implied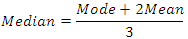 or
or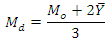 Using above, obviously, we have
Using above, obviously, we have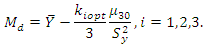 | (3.1) |
where for univariate population, 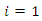 and for the bivariate population
and for the bivariate population 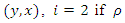 is highly positive and
is highly positive and 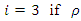 is highly negative, which is a new parametric relationship for population median.Using above parametric relationship for population median, we here propose three different estimators of
is highly negative, which is a new parametric relationship for population median.Using above parametric relationship for population median, we here propose three different estimators of 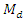 as
as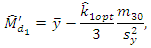 | (3.2) |
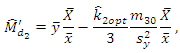 | (3.3) |
and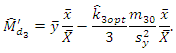 | (3.4) |
Up to terms of order 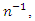 the biases and MSE’s of
the biases and MSE’s of 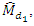
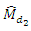 and
and 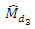 are given as
are given as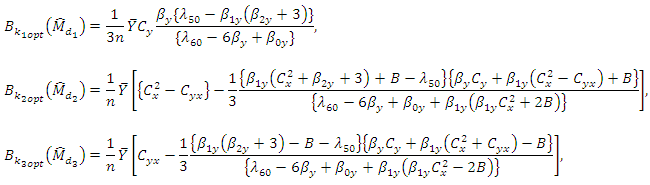 The biases of above estimators are of order
The biases of above estimators are of order 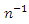 so their contribution to the MSE’s will be of the order
so their contribution to the MSE’s will be of the order 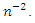 Up to terms of order
Up to terms of order 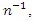 the MSE’s are
the MSE’s are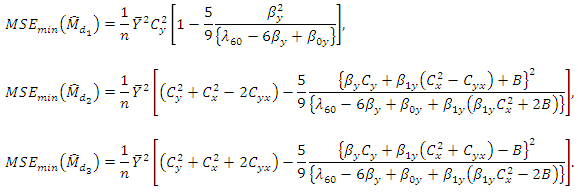 Among the three estimators, the most efficient is
Among the three estimators, the most efficient is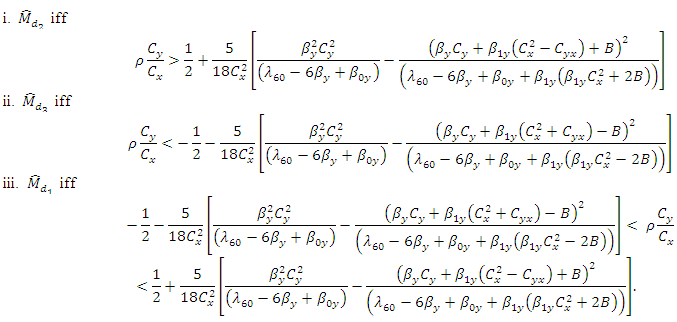
4. Empirical and Simulation Studies
4.1. Empirical Studies
To illustrate the result numerically, we have made computations for 10 populations taken from literature, by using Microsoft Excel 2010.Empirical study-IThe source of the populations, the nature of the variables, the values of 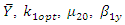 and
and  are listed in Table 1.
are listed in Table 1.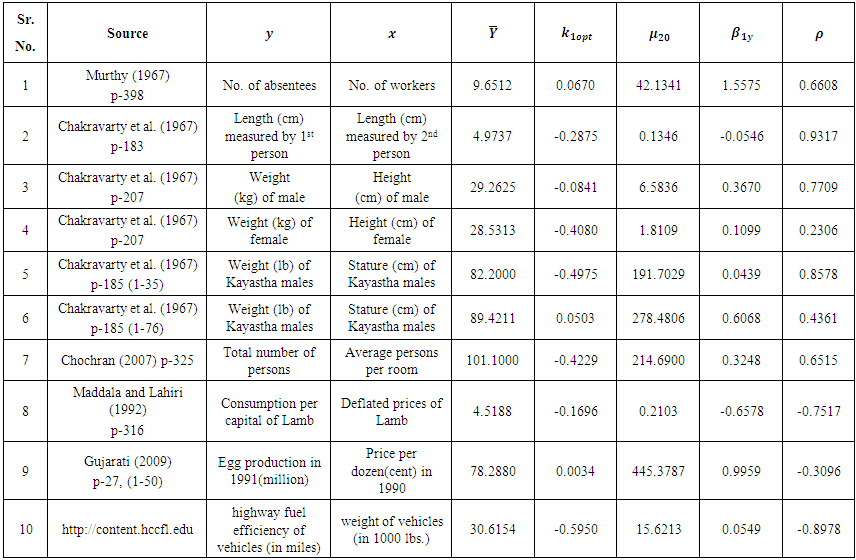 | Table 1. Description of populations |
In Table 2, we have given the true value of population Median 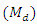 and values of the population median obtained by using the new parametric functional relationship of
and values of the population median obtained by using the new parametric functional relationship of 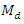 and the efficiencies of proposed estimators are given in Table 3.
and the efficiencies of proposed estimators are given in Table 3.Table 2. Values of population median
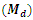 and their values obtained from new parametric relationship and their values obtained from new parametric relationship
 |
| |
|
Table 3. Up to terms of
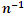 MSE of MSE of
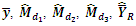 and and
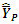
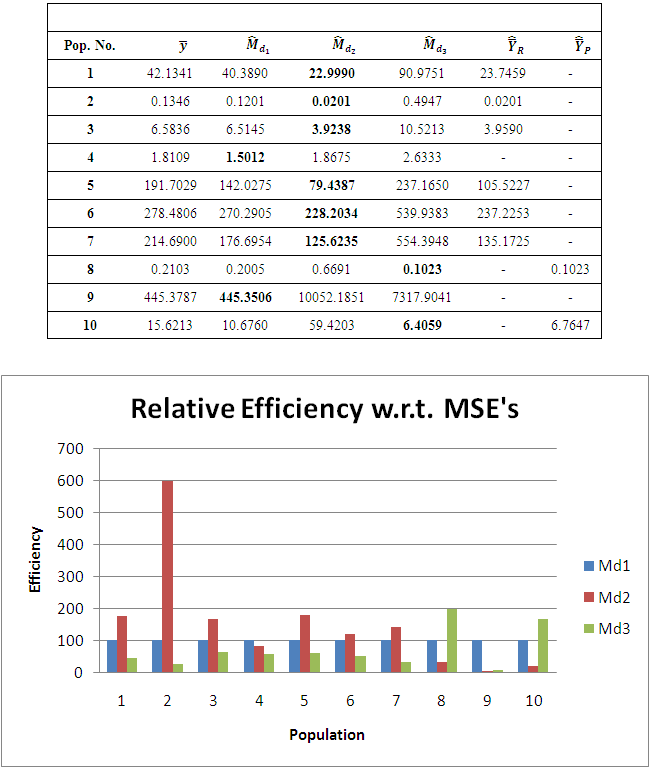 |
| |
|
From Table 2, we observe that the values obtained from the new parametric functional relationship for median i.e. 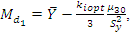 are very close to the true value of the population median
are very close to the true value of the population median 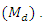 The small amount of errors
The small amount of errors 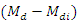 is due to the fact that we are using the optimum value of
is due to the fact that we are using the optimum value of 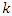 (by minimizing MSE up to order
(by minimizing MSE up to order 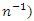 not the exact one. So, empirically, this relation is verified and the percentage of relative margin of these errors presented in bar graph.From Table 3, we observe that in the sampling theory, for the bivariate population, the known value of
not the exact one. So, empirically, this relation is verified and the percentage of relative margin of these errors presented in bar graph.From Table 3, we observe that in the sampling theory, for the bivariate population, the known value of 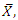 increases the accuracy of the estimators of population median
increases the accuracy of the estimators of population median 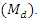 We note that the MSE’s of all
We note that the MSE’s of all 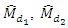 and
and 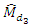 are less than
are less than 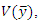 at the same time MSE’s of
at the same time MSE’s of 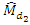 and
and 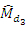 are less than
are less than 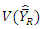 and
and 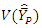 respectively when conditions (i), (ii) and (iii) are satisfied and the relative efficiencies of
respectively when conditions (i), (ii) and (iii) are satisfied and the relative efficiencies of 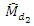 and
and 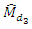 are also shown through bar graph.Empirical Study-IITheoretically, the proposed estimators of
are also shown through bar graph.Empirical Study-IITheoretically, the proposed estimators of 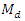 cannot be compared with the existing estimators because the techniques of estimators of
cannot be compared with the existing estimators because the techniques of estimators of 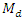 and the parameters involved in MSE’s are different. So an empirical study has been done to check the performance of the proposed estimators over the existing ones, we consider the two populations, which are considered by Singh and Solanki (2013).The minimum MSE’s of proposed estimators and estimators considered by Singh and Solanki (2013) are given in Table 4.
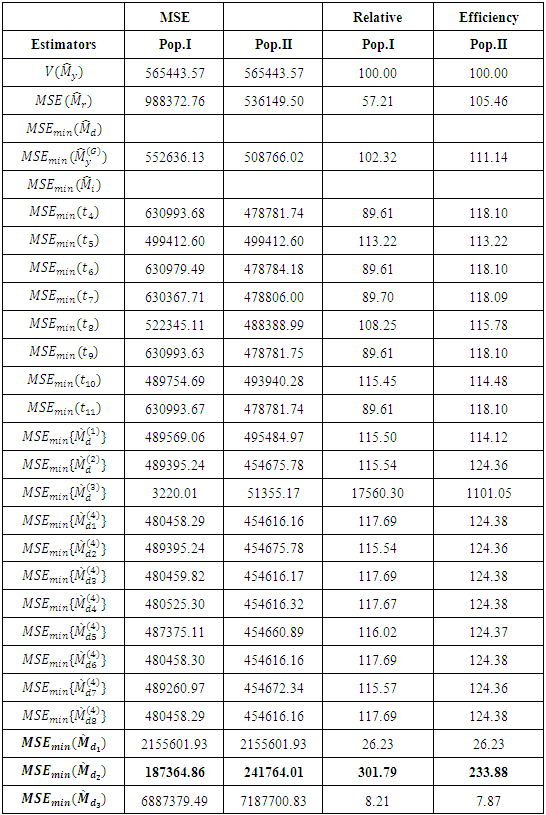
and the parameters involved in MSE’s are different. So an empirical study has been done to check the performance of the proposed estimators over the existing ones, we consider the two populations, which are considered by Singh and Solanki (2013).The minimum MSE’s of proposed estimators and estimators considered by Singh and Solanki (2013) are given in Table 4. Table 4. MSE and Relative Efficiencies of Population Median
 |
| |
|
From Table 4, we observe that, the efficiency of the proposed estimator 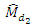 (appropriate estimator because
(appropriate estimator because 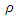 is highly positive), which is very much high as compared to existing ones.
is highly positive), which is very much high as compared to existing ones.
4.2. Simulation Study
A simulation study as been carried out using the software 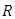 that verifies the theoretical results of our work. For this purpose, 100,000 samples have drawn from different gamma distributions, which are skewed. In this case the actual value of
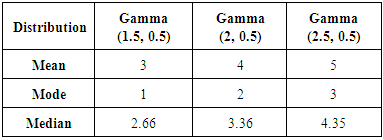
that verifies the theoretical results of our work. For this purpose, 100,000 samples have drawn from different gamma distributions, which are skewed. In this case the actual value of 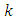 is used which is equal to 0.5. For these distributions, we check the behavior of the estimator for different sample sizes. The values of population mean, median and mode for different gamma distributions are shown in Table 5.
is used which is equal to 0.5. For these distributions, we check the behavior of the estimator for different sample sizes. The values of population mean, median and mode for different gamma distributions are shown in Table 5.Table 5. Descriptive Statistics
 |
| |
|
Using simulation study we compared the existing estimator of sample median 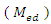 with the proposed estimator
with the proposed estimator 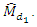 The expected values and MSE’s of these estimators are shown in Table 6.
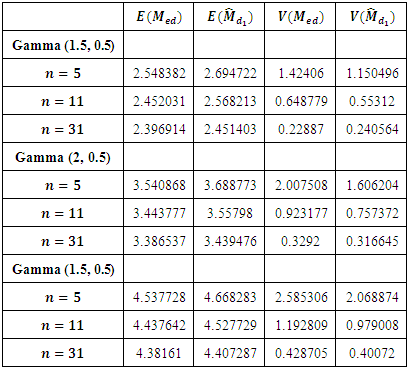
The expected values and MSE’s of these estimators are shown in Table 6.Table 6. The Expected and MSE values of the Estimators
 |
| |
|
Some results based on simulation study1. Biases and MSE’s for both the estimators decrease as the sample size in- creases.2. The proposed estimator slightly more biased than the existing estimator.3. Variance of proposed estimator always less than the variance of existing estimator, which shows that the proposed estimator is more stable than the existing estimator (sample median).
5. Conclusions
Theoretically and the with the support of empirical and simulation studies, we can say that the developed new parametric relationship for population median i.e. 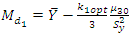 is true. Using this new parametric relationship for population median, we can construct the different estimators for population median. This different technique of estimation of population median is very simple and efficient as compared to the existing ones. Further, one more interesting conclusion from this study is that the proposed conventional consistent estimator
is true. Using this new parametric relationship for population median, we can construct the different estimators for population median. This different technique of estimation of population median is very simple and efficient as compared to the existing ones. Further, one more interesting conclusion from this study is that the proposed conventional consistent estimator 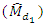 of population median is more stable than the mean per unit estimator of population mean.
of population median is more stable than the mean per unit estimator of population mean.
References
| [1] | Al S, Cingi H (2010) New estimators for the population median in simple random sampling. In: Proceedings of the Tenth Islamic Countries Conference on Statistical Sciences (ICCS-X): Vol-1, pp 375-383. |
| [2] | Chakravarty IM, Laha RG, Roy J (1967) Handbook of Methods of Applied Statistics: Techniques of Computation, Descriptive Methods, and Statistical Inference. John Wiley & Sons. |
| [3] | Cochran WG (2007) Sampling Techniques, 3rd edn. Wiley Student Edition. |
| [4] | Doodson AT (1917) Iii. relation of the mode, median and mean in frequency curves. Biometrika 11(4):425-429. |
| [5] | Garcı MR, Cebrián AA (2001) On estimating the median from survey data using multiple auxiliary information. Metrika, 54(1): 59-76. |
| [6] | Gujarati DN (2009) Basic econometrics. Tata Mc Graw-Hills Education. |
| [7] | Kuk AY, Mak TK (1989) Median estimation in the presence of auxiliary information. Journal of the Royal Statistical Society. Series B (Methodological), 51(2): 261-269. |
| [8] | Maddala GS, Lahiri K (1992) Introduction to econometrics, vol. 2.Macmillan New York. |
| [9] | Mak TK, Kuk AY (1993) A new method for estimating finite-population quantiles using auxiliary information, The Canadian Journal of Statistics, 21(1):29-38. |
| [10] | Murthy MN (1967) Sampling theory and methods. Statistical Publishing Society. |
| [11] | Sharma MK, Brar SS, Kaur H (2016) Estimators of population mode using new parametric relationship for mode. International Journal of Probability and Statistics 5(1): 18-24. |
| [12] | Singh HP, Solanki RS (2013) Some Classes of Estimators for the Population Median Using Auxiliary Information. Communications in Statistics-Theory and Methods, 42(23): 4222-4238. |
| [13] | Singh HP, Sidhu SS, Singh S (2006) Median estimation with known interquartile range of auxiliary variable. Int. J. Appl. Math. Statist, 4:68-80. |
| [14] | Srivastava SK, Jhajj HS (1983) A class of estimators of the population mean using multi-auxiliary information. Cal. Stat. Assoc. Bull, 32:47-56. |


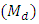 and then propose conventional consistent, ratio-type and product-type estimators of
and then propose conventional consistent, ratio-type and product-type estimators of 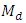 under different situations. The expression for their optimum biases and minimum mean square errors (MSE’s) are obtained, up to terms of order
under different situations. The expression for their optimum biases and minimum mean square errors (MSE’s) are obtained, up to terms of order 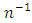 and compared with each other. Empirically, we have checked the authenticity of the relationship for
and compared with each other. Empirically, we have checked the authenticity of the relationship for 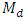 and also the gain in efficiencies of the proposed estimators with each other and existing ones are illustrated.
and also the gain in efficiencies of the proposed estimators with each other and existing ones are illustrated.
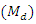 using known information of population median of the auxiliary variable. Empirically, they studied the 22 estimators. In this paper, we first establish the new parametric relationship for population median
using known information of population median of the auxiliary variable. Empirically, they studied the 22 estimators. In this paper, we first establish the new parametric relationship for population median 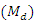 and propose three estimators of
and propose three estimators of 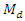 under different situations. This technique of estimation of population median is different from the existing one given by Kuk and Mak (1989), which is very simple and efficient. Up to terms of order
under different situations. This technique of estimation of population median is different from the existing one given by Kuk and Mak (1989), which is very simple and efficient. Up to terms of order 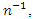 the optimum biases and minimum MSE’s of the proposed estimators are obtained and compared with each other. Empirically, we have done two studies, first to check the authenticity of the relationship for
the optimum biases and minimum MSE’s of the proposed estimators are obtained and compared with each other. Empirically, we have done two studies, first to check the authenticity of the relationship for 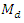 and to have the rough idea about the efficiencies of proposed estimators with each other. Secondly, to compare the efficiencies of the proposed estimators with existing ones as the techniques of estimation and parameters involved in their minimum MSE’s are different.
and to have the rough idea about the efficiencies of proposed estimators with each other. Secondly, to compare the efficiencies of the proposed estimators with existing ones as the techniques of estimation and parameters involved in their minimum MSE’s are different.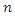 is drawn from a finite population of size
is drawn from a finite population of size 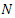 without replacement and observations on both study variables
without replacement and observations on both study variables 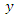 and auxiliary variable
and auxiliary variable 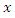 are taken. Let the values of variable
are taken. Let the values of variable 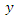 and
and 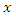 be denoted by
be denoted by 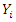 and
and 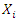 respectively on the
respectively on the 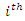 unit of the population
unit of the population 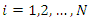 and the corresponding small letters
and the corresponding small letters 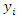 and
and 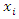 denote the sample values corresponding to the
denote the sample values corresponding to the 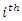 unit in the sample.Taking,
unit in the sample.Taking,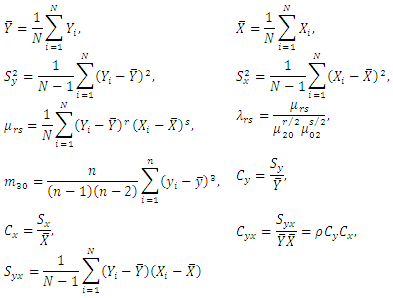 Obviously
Obviously Defining,
Defining,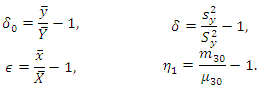 For the sake of simplicity, assume that
For the sake of simplicity, assume that  is large enough as compares to
is large enough as compares to  so that finite population correction (fpc) terms are ignored throughout.For the given SRSWOR, we have the following expectations,
so that finite population correction (fpc) terms are ignored throughout.For the given SRSWOR, we have the following expectations,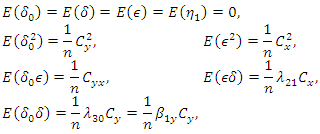 and up to terms of order
and up to terms of order 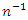
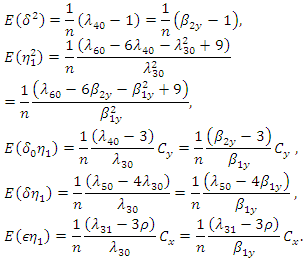
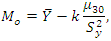 where
where 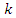 is unknown constant to be determined.Sharma et al. (2016) also proposed three estimators of
is unknown constant to be determined.Sharma et al. (2016) also proposed three estimators of 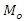 under the three different situations as
under the three different situations as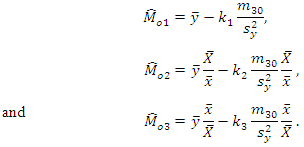 They determined the optimum value of
They determined the optimum value of 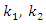 and
and 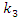 by minimizing the MSE’s of respective estimators as
by minimizing the MSE’s of respective estimators as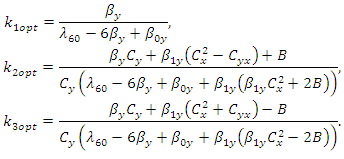 where,
where,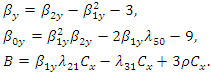 Note that
Note that 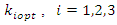 are further functions of unknown population parameters. Srivastava and Jhajj (1983) have shown that if we replace the parameters involved in the optimum value of the unknown constant by their consistent estimators then up to terms of order
are further functions of unknown population parameters. Srivastava and Jhajj (1983) have shown that if we replace the parameters involved in the optimum value of the unknown constant by their consistent estimators then up to terms of order  the MSE remains the same. Therefore, the presence of unknown parameters in the optimum values of the constants will not create any problem for practical use of the proposed estimators.Let
the MSE remains the same. Therefore, the presence of unknown parameters in the optimum values of the constants will not create any problem for practical use of the proposed estimators.Let 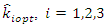 be the values when parameters are replaced by their consistent estimators in
be the values when parameters are replaced by their consistent estimators in 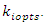 So then the estimators reduces to
So then the estimators reduces to 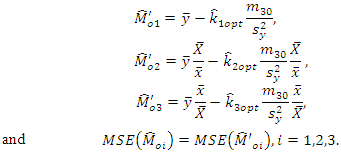 For moderately skewed distribution, Doodson (1917) suggested the empirical relationship as
For moderately skewed distribution, Doodson (1917) suggested the empirical relationship as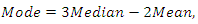 which is also known as Karl Pearson empirical relation between mean, median and mode.That implied
which is also known as Karl Pearson empirical relation between mean, median and mode.That implied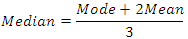 or
or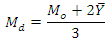 Using above, obviously, we have
Using above, obviously, we have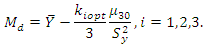
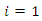 and for the bivariate population
and for the bivariate population 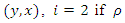 is highly positive and
is highly positive and 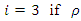 is highly negative, which is a new parametric relationship for population median.Using above parametric relationship for population median, we here propose three different estimators of
is highly negative, which is a new parametric relationship for population median.Using above parametric relationship for population median, we here propose three different estimators of 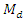 as
as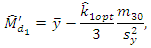
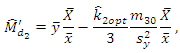
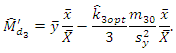
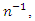 the biases and MSE’s of
the biases and MSE’s of 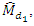
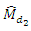 and
and 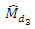 are given as
are given as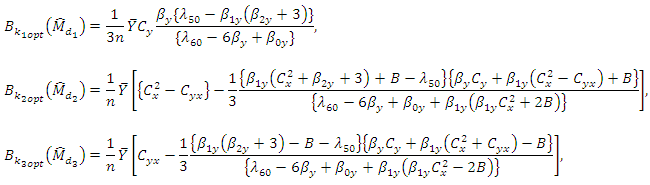 The biases of above estimators are of order
The biases of above estimators are of order 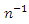 so their contribution to the MSE’s will be of the order
so their contribution to the MSE’s will be of the order 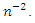 Up to terms of order
Up to terms of order 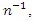 the MSE’s are
the MSE’s are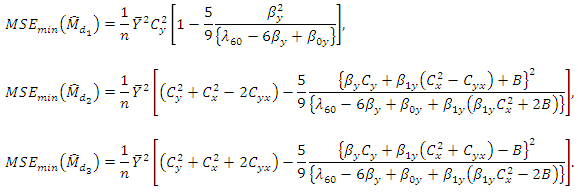 Among the three estimators, the most efficient is
Among the three estimators, the most efficient is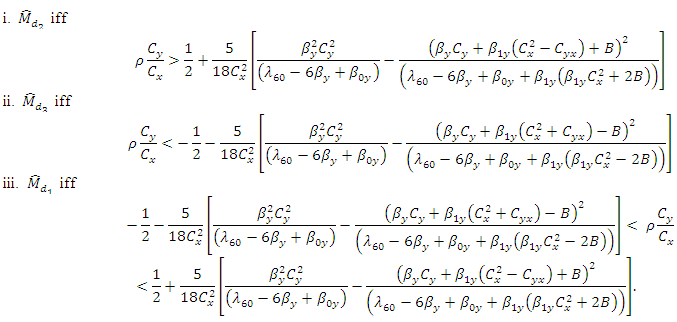
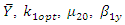 and
and 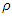 are listed in Table 1.
are listed in Table 1.
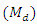 and values of the population median obtained by using the new parametric functional relationship of
and values of the population median obtained by using the new parametric functional relationship of 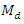 and the efficiencies of proposed estimators are given in Table 3.
and the efficiencies of proposed estimators are given in Table 3.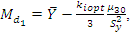 are very close to the true value of the population median
are very close to the true value of the population median 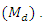 The small amount of errors
The small amount of errors 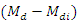 is due to the fact that we are using the optimum value of
is due to the fact that we are using the optimum value of 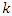 (by minimizing MSE up to order
(by minimizing MSE up to order 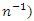 not the exact one. So, empirically, this relation is verified and the percentage of relative margin of these errors presented in bar graph.From Table 3, we observe that in the sampling theory, for the bivariate population, the known value of
not the exact one. So, empirically, this relation is verified and the percentage of relative margin of these errors presented in bar graph.From Table 3, we observe that in the sampling theory, for the bivariate population, the known value of 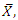 increases the accuracy of the estimators of population median
increases the accuracy of the estimators of population median 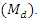 We note that the MSE’s of all
We note that the MSE’s of all 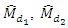 and
and 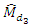 are less than
are less than 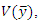 at the same time MSE’s of
at the same time MSE’s of 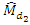 and
and 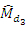 are less than
are less than 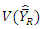 and
and 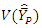 respectively when conditions (i), (ii) and (iii) are satisfied and the relative efficiencies of
respectively when conditions (i), (ii) and (iii) are satisfied and the relative efficiencies of 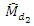 and
and 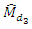 are also shown through bar graph.Empirical Study-IITheoretically, the proposed estimators of
are also shown through bar graph.Empirical Study-IITheoretically, the proposed estimators of 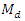 cannot be compared with the existing estimators because the techniques of estimators of
cannot be compared with the existing estimators because the techniques of estimators of 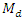 and the parameters involved in MSE’s are different. So an empirical study has been done to check the performance of the proposed estimators over the existing ones, we consider the two populations, which are considered by Singh and Solanki (2013).The minimum MSE’s of proposed estimators and estimators considered by Singh and Solanki (2013) are given in Table 4.
and the parameters involved in MSE’s are different. So an empirical study has been done to check the performance of the proposed estimators over the existing ones, we consider the two populations, which are considered by Singh and Solanki (2013).The minimum MSE’s of proposed estimators and estimators considered by Singh and Solanki (2013) are given in Table 4. 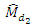 (appropriate estimator because
(appropriate estimator because 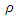 is highly positive), which is very much high as compared to existing ones.
is highly positive), which is very much high as compared to existing ones. 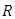 that verifies the theoretical results of our work. For this purpose, 100,000 samples have drawn from different gamma distributions, which are skewed. In this case the actual value of
that verifies the theoretical results of our work. For this purpose, 100,000 samples have drawn from different gamma distributions, which are skewed. In this case the actual value of 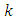 is used which is equal to 0.5. For these distributions, we check the behavior of the estimator for different sample sizes. The values of population mean, median and mode for different gamma distributions are shown in Table 5.
is used which is equal to 0.5. For these distributions, we check the behavior of the estimator for different sample sizes. The values of population mean, median and mode for different gamma distributions are shown in Table 5.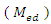 with the proposed estimator
with the proposed estimator 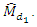 The expected values and MSE’s of these estimators are shown in Table 6.
The expected values and MSE’s of these estimators are shown in Table 6.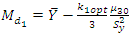 is true. Using this new parametric relationship for population median, we can construct the different estimators for population median. This different technique of estimation of population median is very simple and efficient as compared to the existing ones. Further, one more interesting conclusion from this study is that the proposed conventional consistent estimator
is true. Using this new parametric relationship for population median, we can construct the different estimators for population median. This different technique of estimation of population median is very simple and efficient as compared to the existing ones. Further, one more interesting conclusion from this study is that the proposed conventional consistent estimator 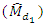 of population median is more stable than the mean per unit estimator of population mean.
of population median is more stable than the mean per unit estimator of population mean. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML and their values obtained from new parametric relationship
and their values obtained from new parametric relationship
 MSE of
MSE of 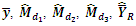 and
and