A. Danbaba 1, Shehu A. 2
1Department of Mathematics, Usmanu Danfodiyo University, Sokoto, Nigeria
2Department of Mathematical Sciences & IT, Federal University, Dutsinma, Nigeria
Correspondence to: A. Danbaba , Department of Mathematics, Usmanu Danfodiyo University, Sokoto, Nigeria.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Experiments are repeatedly carried out at several times, locations (environments) or season (period) with one or more treatments in common to each experiment, to investigate the interaction between the treatments and location (enviroment) of the experiment or treatments and times or season (period). The analysis of such experiments are carry out using combined analysis of technique. This paper proposed combined analysis of experiments conducted, using Sudoku Square designs of odd order when some treatments are common to all the experiments.
Keywords:
Combined analysis, Sudoku Square design, Multi-experiments
Cite this paper: A. Danbaba , Shehu A. , On the Combined Analysis of Sudoku Square Designs with Some Common Treatments, International Journal of Statistics and Applications, Vol. 6 No. 6, 2016, pp. 347-351. doi: 10.5923/j.statistics.20160606.02.
1. Introduction
Experiment may be conducted with the aid of randomized block designs or Latin square designs or balanced incomplete designs over different environments. The reason may be due to lack of space that would accomodate all the experimental plots or with the underlying condition that the experiments must be carried out at different locations (environment) or different seasons, whatever may be the reason, the major aim is to do joint analysis of the data obtained from these multi-environments instead of doing the analysis separately or individually (Albassan and Ali, 2014) and one of the advantages of multi-environment analysis is that it increases the accuracy of evaluation (hence the accuracy of selection). The joy derived accuracy is a function of several factors or treatments (Cullis et al., 2010). The other reasons are estimation of consistency of treatments effects for a particular environments over large population of environments (Blouin et al., 2011).Gomes and Gumarie (1958) considers the intra-block analysis of a group of experiments in complete randomized block, where treatments applied are all different but some treatments are common to the whole experiment, some examples were given, separate tables of analysis and the table of the combined analysis were also given. They further gave the condition that must be met before combined analysis can be carried out, as such, if the residual variance estimates from separate analyses are not too different a joint analysis can be carried out for the whole set of the experiments.Pavate (1961) used the same approach and obtained the combined analysis of balancded incomplete block design with some common treatments applied to all the experiments of the multi-environment, methods of obtaining adjusted treatment sumof square was explained and illustration was given.Giri (1963) discusses combination of the method used by Pavate (1961), he said Pavate method can be used to analyzed data from combined data of set of Youden Squares when some treatments are common while that of Gomes and Gumarie can be used for combined analysis of a set of latin square when some treatments are common to all the experiments. Mcintosh (1983) gave a clue for the analysis of combined experiments, the tables indicate sources of variation, degree of freedom and F-ratio for factors and split-plot experiment combined over location and / or year. F-ratios for the fixed, mixed and random model were as well presented. Paul (1989) discusses method used for the combined analysis when treatment s are used to represents levels of quantitative factor but differ among experiments. Multiple regresion analysis was used when a continuous variable represents treatment levels, classification variables represents experiments and product of the continuous and classification variables present differences among experiments. Analyses for experiments combined across years and location are presented by Moore and Dixon (2015). This is similar to Mcintosh (1983) but the F tests are specific based on the alternative about assumption about mixed interactions, i.e the fixed effects do not sum to zero in a mixed interaction. Although, there is little research on the combined analysis of Sudoku square designs, until recent time, Danbaba (2016) presented a paper on the combined analysis of Sudoku Square Designs, of odd order with same experimental treatments. A combined analysis of data from multi-environments experiment was presented using Sudoku square designs and modified linear model and the tables of analysis were as well presented.Sudoku is the abbreviation of the japanese longer phrase “suji wa dokushin ni kagiru” which means the digit must occur only once (Berthier, 2007; Gordon and Longo, 2006). Sudoku puzzle is a very popular game, the objective of the game is to complete a 9 9 grid with digits from 1 to 9. Each digit must appear once only in each row, each column and each of the 3 3 boxes see Bailey et al., (2008). Sudoku square design consists of treatments which are arranged in a square array such that each row, column or sub-square of the design contains each of the treatments exactly once (Hui-Dong and Ru-Gen, 2008). Away from the construction process of Sudoku square, mathematical models and statistical method of data analysis were presented by Hui-Dong and Rui-Gen, (2008). He observed that sudoku sqauare design go beyond Latin sqaure design with one additional source of variation i.e box effect.Subramani and Ponnuswamy (2009) came up with an extension of the work done by Hui-Dong and Rui-Gen in 2008, with additional terms in the models and in the sources of variation namely Row-block effect, and column-block effect. They considered Sudoku of order k = m2 and gave detail analysis with illustrative example and the application of Sudoku square to agricultural experiment. If we compare the models by Hui-Dong and Rui-Gen, (2008) and that of Subramani and Ponnuswamy, we observed that Hui-Dong and Rui-Gen did not includes row-block and column-block effects into their analysis but Subramani and Ponnuswamy went ahead to include row-block and column-block effects into their analysis and proposed four differents models with their respective ANOVA tables.This paper proposed combined analysis of multi-environment experiments carried out using Sudoku Square design of odd order when treatments are not the same in all Sudoku square but some treatments are common to the whole set of experiments.
2. Analyses
If we assumed that there 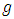 multi-environment experiments each carried –out using Sudoku square design, each with
multi-environment experiments each carried –out using Sudoku square design, each with 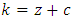 treatments, of which
treatments, of which 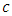 treatments are common to all Sudoku square design multi-environment experiments which connects them out of
treatments are common to all Sudoku square design multi-environment experiments which connects them out of 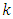 treatments and
treatments and 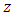 treatments are not common but for the sake of this research it will be called ‘’uncommon’’treatments in each design. The total number of different treatments in each design is then
treatments are not common but for the sake of this research it will be called ‘’uncommon’’treatments in each design. The total number of different treatments in each design is then 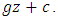 The “uncommon” treatments have
The “uncommon” treatments have 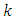 replications because uncommon treatments are limited to a particular Sudoku square design in an experimental environment and the common ones are replicated
replications because uncommon treatments are limited to a particular Sudoku square design in an experimental environment and the common ones are replicated 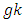 times that is,
times that is, 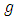 environments
environments 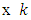 replications. We carry-out analysis of variance for each experiment in the usual way and obtained tests of significant and estimate of effects with errors has suggested by Gomes and Gumarie (1958). If the residual variance estimates are not significantly different a combined analysis can be carried out for the whole set of experiments.Sudoku square design assume that having
replications. We carry-out analysis of variance for each experiment in the usual way and obtained tests of significant and estimate of effects with errors has suggested by Gomes and Gumarie (1958). If the residual variance estimates are not significantly different a combined analysis can be carried out for the whole set of experiments.Sudoku square design assume that having 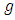 multi-environment experiments each with
multi-environment experiments each with 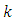 treatments, each occurs only once in each row, column or sub-block or square) such that
treatments, each occurs only once in each row, column or sub-block or square) such that 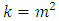 where
where 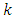 and
and 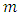 (number of row-block and column-block) are odd see (Subramani and Ponnuswamy 2009). If for example fig 1. is
(number of row-block and column-block) are odd see (Subramani and Ponnuswamy 2009). If for example fig 1. is  Latin square or
Latin square or 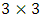 Sudoku square design. Considering the fig 1., the number of row-block and column-block is 3 which is an odd number.
Sudoku square design. Considering the fig 1., the number of row-block and column-block is 3 which is an odd number.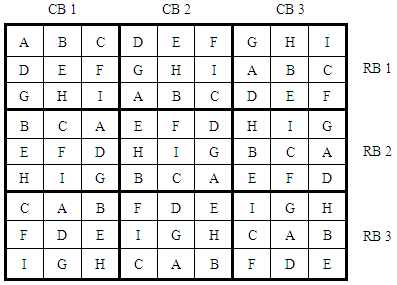 | Figure 1. Typical example of Sudoku square with 3 3 square region |
In this study, (Hui-Dong andRui-Gen, 2008) and (Subramani and Ponnuswamy, 2009) models were modified and combined analysis for each were discussed. For all the models considered in this study, it is assumed that all effects are fixed and only 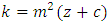 number of treatments is discussed.Model 1Hui-Dong and Rui-Gen (2008) proposed linear model for Sudoku square design and being modified to includes the multi-environment experiment as follows.
number of treatments is discussed.Model 1Hui-Dong and Rui-Gen (2008) proposed linear model for Sudoku square design and being modified to includes the multi-environment experiment as follows.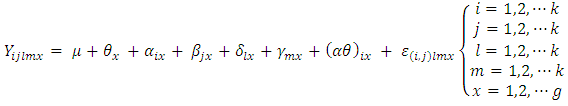 | (1) |
where 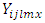 is a obseved value of the plot in the
is a obseved value of the plot in the 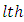 row and
row and 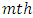 column, subjected to the
column, subjected to the 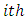 treatment,
treatment, 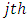 box of the
box of the 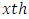 experimental environment;
experimental environment; 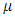 is the grand mean,
is the grand mean, 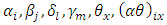 are the main effects of the
are the main effects of the 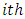 treatment,
treatment, 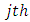 box,
box, 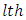 row,
row, 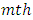 column,
column, 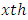 experimental environment and interaction between common treatments and environment respectively and
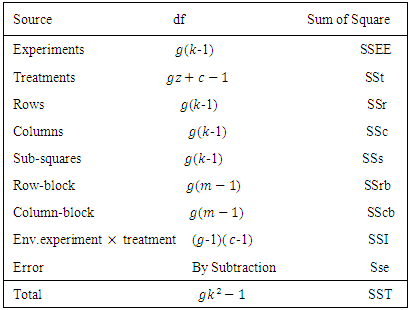
experimental environment and interaction between common treatments and environment respectively and 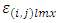 is the random error. Where SSEE is the sum of square of the experimental environment, SSt is the total treatment sum of square for all the multi-environment experiments, SSr is the total row sumof squres for all the multi-environment experiments, SSc the total column sumof squares for all the multi-environment experiments, SSs is the total sub-block sumof squares for all the multi-environment experiments, SSI is the total interaction sumof squares between common treatment and the multi-environment experiments and Sse the total error sumof squares for all the multi-environment experiments.If we let
is the random error. Where SSEE is the sum of square of the experimental environment, SSt is the total treatment sum of square for all the multi-environment experiments, SSr is the total row sumof squres for all the multi-environment experiments, SSc the total column sumof squares for all the multi-environment experiments, SSs is the total sub-block sumof squares for all the multi-environment experiments, SSI is the total interaction sumof squares between common treatment and the multi-environment experiments and Sse the total error sumof squares for all the multi-environment experiments.If we let 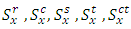 and
and 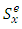 be the
be the 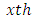 environment row, column, sub-square, treatment, common treatment and error sum of square respectively.
environment row, column, sub-square, treatment, common treatment and error sum of square respectively.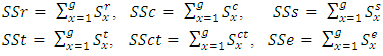 The alternative method of the above can be obtained as follows
The alternative method of the above can be obtained as follows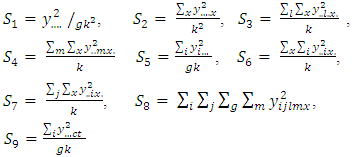 The computational analysis of the sum of the squares for the remaining models (2-5) are almost the same with model 1 and therefor not discussed in this paper for the detail computation analysis check Subramani and Ponnuswamy (2012) for separate analysis.
The computational analysis of the sum of the squares for the remaining models (2-5) are almost the same with model 1 and therefor not discussed in this paper for the detail computation analysis check Subramani and Ponnuswamy (2012) for separate analysis.Table 1. ANOVA Table for the combined analysis of the set of Sudoku square design for model 1
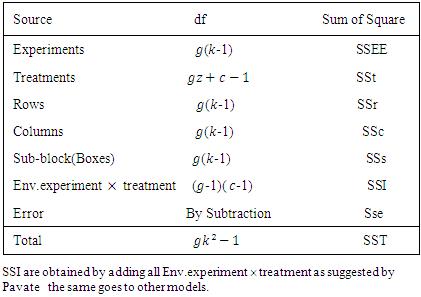 |
| |
|
Model 2: The modification of Type I of Subramani & Ponnuswamy linear model is as follows. We will assume that row, column, and treatments effect as in the latin square, also in addition to the assumption, Row block, column block, square effects, environmental experiments and interaction between common treatments and environmental experiments. 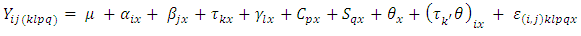 | (2) |
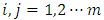 and
and 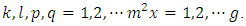 Where
Where 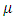 is general mean,
is general mean, 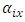 is
is 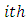 row-block effect in
row-block effect in 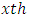 environmental experiment,
environmental experiment, 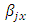 is
is 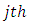 column-block effect in
column-block effect in 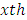 environmental experiment,
environmental experiment, 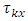 is
is 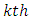 treatment effect in
treatment effect in 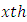 environmental experiment,
environmental experiment, 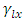 is the
is the 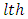 row effect in
row effect in 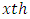 environmental experiment,
environmental experiment, 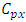 is
is 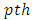 the column effect in
the column effect in 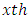 environmental experiment,
environmental experiment, 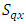 is the
is the 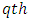 sub-square effect in
sub-square effect in 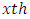 environmental experiment,
environmental experiment, 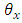 is the
is the 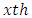 environmental experiment,
environmental experiment, 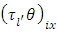 is the interaction between
is the interaction between 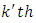 common treatment and
common treatment and 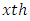 environmental experiment and
environmental experiment and 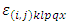 error component with mean zero and constant variance.
error component with mean zero and constant variance.Table 2. ANOVA Table for the combined analysis of the set of Sudoku square design for model 2
 |
| |
|
Model 3: The modification of Type II of Subramani & Ponnuswamy linear model is as follows. The model assumed that row effects are nested in the row block effect and the column effects are nested in the column block effects. In addition to, environmental experiments and interaction between common treatments and environmental experiments.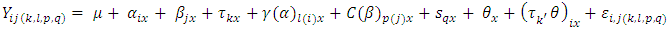 | (3) |
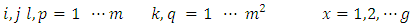 Where
Where 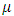 is general mean,
is general mean, 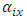 is
is 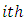 row-block effect in
row-block effect in 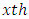 environmental experiment,
environmental experiment, 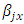 is
is 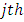 column-block effect in
column-block effect in 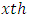 environmental experiment,
environmental experiment, 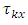 is
is 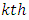 treatment effect in
treatment effect in 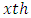 environmental experiment,
environmental experiment, 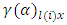 is the
is the 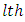 row effect nested in
row effect nested in 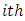 row-block in
row-block in 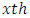 environmental experiment,
environmental experiment, 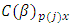 is the
is the 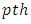 column effect in
column effect in 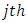 column-blockin
column-blockin 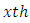 environmental experiment,
environmental experiment, 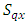 is the
is the 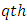 sub-square effect in
sub-square effect in 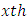 environmental experiment,
environmental experiment, 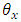 is the
is the 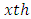 environmental experiment,
environmental experiment, 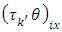 is the interaction between
is the interaction between 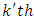 common treatment and
common treatment and 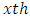 environmental experiment and
environmental experiment and 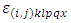 error component with mean zero and constant variance.
error component with mean zero and constant variance.Table 3. ANOVA Table for the combined analysis of the set of Sudoku square design for model 3
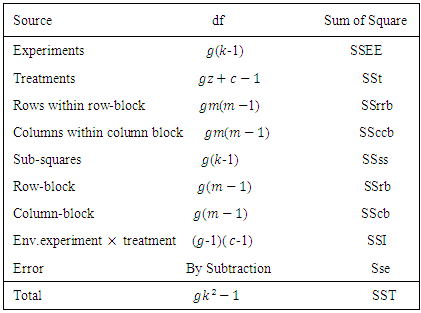 |
| |
|
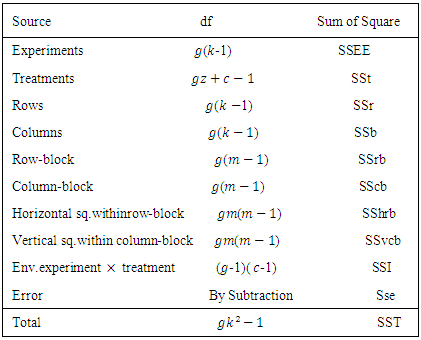
Model 4: The modification of Type III of Subramani & Ponnuswamy linear model is as follows. The model assumes that the horizontal square effects are nested in the row block and vertical Square effects are nested in the column block effects. In addition to, environmental experiments and interaction between common treatments and environmental experiments.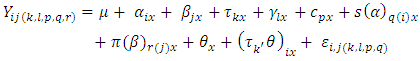 | (4) |
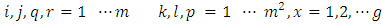 Where
Where 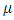 is general mean,
is general mean, 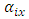 is
is 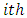 row-block effect in
row-block effect in 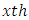 environmental experiment,
environmental experiment, 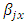 is
is 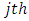 column-block effect in
column-block effect in 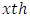 environmental experiment,
environmental experiment, 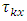 is
is 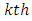 treatment effect in
treatment effect in 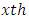 environmental experiment,
environmental experiment, 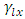 is the
is the 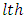 row effect in
row effect in 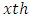 environmental experiment,
environmental experiment, 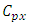 is
is 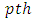 the column effect in
the column effect in 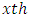 environmental experiment,
environmental experiment, 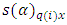 is the
is the 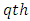 horizontal square effect nested in
horizontal square effect nested in 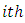 row-block in
row-block in 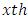 environmental experiment,
environmental experiment, 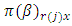 is the
is the 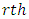 vertical square effect nested in
vertical square effect nested in 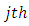 column-block in
column-block in 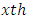 environmental experiment,
environmental experiment, 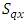 is the
is the 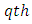 sub-square effect in
sub-square effect in 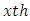 environmental experiment,
environmental experiment, 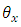 is the
is the 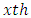 environmental experiment,
environmental experiment, 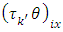 is the interaction between
is the interaction between 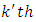 common treatment and
common treatment and 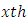 environmental experiment and
environmental experiment and 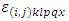 error component with mean zero and constant variance.Model 5: The modification of Type IV of Subramani & Ponnuswamy linear model is as follows. In the model below, it is assumed that the row effects and horizontal square effects are nested in the row block and the column effects and the vertical square effects are nested in the column block effect
error component with mean zero and constant variance.Model 5: The modification of Type IV of Subramani & Ponnuswamy linear model is as follows. In the model below, it is assumed that the row effects and horizontal square effects are nested in the row block and the column effects and the vertical square effects are nested in the column block effect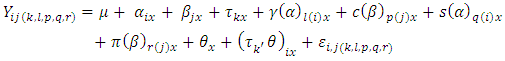 | (5) |
where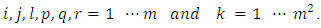 Where
Where 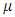 is general mean,
is general mean, 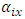 is
is 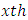 row-block effect in
row-block effect in 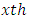 environmental experiment,
environmental experiment, 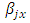 is
is 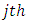 column-block effect in
column-block effect in 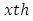 environmental experiment,
environmental experiment, 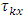 is
is 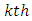 treatment effect in
treatment effect in 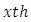 environmental experiment,
environmental experiment, 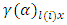 is the
is the 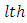 row effect nested in
row effect nested in 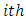 row-block in
row-block in 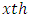 environmental experiment,
environmental experiment, 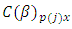 is the
is the 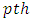 column effect in
column effect in 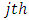 column-block in
column-block in 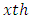 environmental experiment
environmental experiment 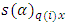 is the
is the 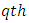 horizontal square effect nested in
horizontal square effect nested in 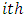 row-block in
row-block in 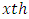 environmental experiment,
environmental experiment, 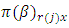 is the
is the 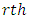 vertical square effect nested in
vertical square effect nested in 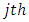 column-block in
column-block in 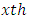 environmental experiment,
environmental experiment, 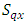 is the
is the 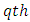 sub-square effect in
sub-square effect in 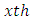 environmental experiment,
environmental experiment, 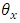 is the
is the 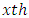 environmental experiment,
environmental experiment, 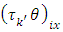 is the interaction between
is the interaction between 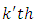 common treatment and
common treatment and 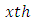 environmental experiment and
environmental experiment and 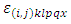 error component with mean zero and constant variance.
error component with mean zero and constant variance.Table 4. ANOVA Table for the combined analysis of the set of Sudoku square design for model 4
 |
| |
|
Table 5. ANOVA Table for the combined analysis of the set of Sudoku square design for model 5
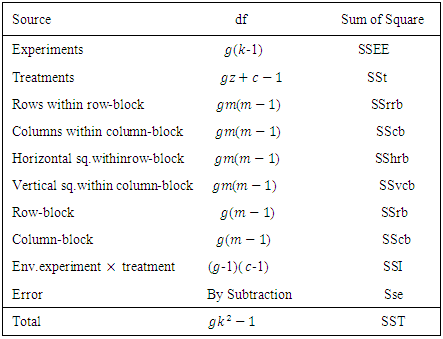 |
| |
|
3. Conclusions
The methods of combining analysis of Sudoku square design of odd order has been presented when experiments were carried-out in a 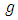 enviroments when treatments are not same in all experiments, but some treatments common in all the experiments. Five Sudoku design linear models were modified by adding environmental effects and interaction between common treatments and environmental effects terms to the models. The sum of square for rows, columns and sub-squares of
enviroments when treatments are not same in all experiments, but some treatments common in all the experiments. Five Sudoku design linear models were modified by adding environmental effects and interaction between common treatments and environmental effects terms to the models. The sum of square for rows, columns and sub-squares of 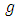 environments are obtained by summing all the individual sum of squares for rows, columns and sub-square respectively. Similarly, the same are done to obtain sum of squares for row-blocks, column-blocks, rows within row-block, column within column-block, horizontal square within row-block and vertical square within column-block respectively.
environments are obtained by summing all the individual sum of squares for rows, columns and sub-square respectively. Similarly, the same are done to obtain sum of squares for row-blocks, column-blocks, rows within row-block, column within column-block, horizontal square within row-block and vertical square within column-block respectively.
References
| [1] | A. Danbaba (2016). Combined Analysis of Sudoku Square Designs with Same Treatments. International Journal of Mathematical, Computational, Physical, Electrical and Computer Engineering Vol:10, No:4, 155-159. |
| [2] | Blouin, D.C., Webster, E.P., and Bond, J.A. (2011). On the analysis of combined experiments weed Technology 2011 25(1), 165-169. |
| [3] | Bailey, R.A., Cameron P.J. and Connelly R. (2008). Sudoku, Gerchte Designs, Resolutions, Affine Space, Spreads Reguli and Hamming Codesread. American Math. Monthly. |
| [4] | Berthier D. (2007). The Hidden Logic of Sudoku, 2nd edition, Lulu morisville NC. |
| [5] | Giri, N.C. (1963) Note on the Combined Analysis of Youden Squares and of Latin Square Designs with some Common Treatments Biometrics 19(1), 171-174. |
| [6] | Gomes, F.F and Guimares, R.F. (1958). Joint analysis of experiments incomplete randomized blockswith some common treatments Biometrics 14, 521-526. |
| [7] | Gordon P. and F. Longo (2006). Mensa Guide to solving Sudoku Sterling, New York. |
| [8] | Hui-Dong M. and Ru-Gen, X. (2008). Sudoku Square- a New Design in field Experiment, Acta Agron Sin, 34(9), 1489–1493. |
| [9] | McIntosh, M.S. (1983). Analysis of combined experiments. Agron. J. 75: 153-155. |
| [10] | M.S. Albassam and M.A. Ali (2014). Test Statistics for combined treatment contrast under heterogeneous error variances and Latin square design. Pakistan Journal of Statistics. Vol.30(3),345-360 |
| [11] | Moore, K.J. and Dixion P.M. (2015). Analysis of combined experiments Revisted, Agronomy Journal, 107(2),763-771. |
| [12] | Paul N. H. and Mario, R. P. (1989). Combined analysis of experiments when treatments differ among experiments. Annual conference on applied Statistics in agriculture.paper 20. |
| [13] | Pavate, M.V. (1961). Combined Analysis of Balanced incomplete block Designs with some common treatments. Biometrics, 17(1), 111-119. |
| [14] | Subramani, J. and K.N. Ponnuswamy (2009). Construction and Analysis of Sudoku designs.Model Assisted Statistics and Applications, 4(4),287-301. |



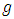 multi-environment experiments each carried –out using Sudoku square design, each with
multi-environment experiments each carried –out using Sudoku square design, each with 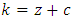 treatments, of which
treatments, of which 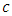 treatments are common to all Sudoku square design multi-environment experiments which connects them out of
treatments are common to all Sudoku square design multi-environment experiments which connects them out of 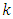 treatments and
treatments and 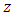 treatments are not common but for the sake of this research it will be called ‘’uncommon’’treatments in each design. The total number of different treatments in each design is then
treatments are not common but for the sake of this research it will be called ‘’uncommon’’treatments in each design. The total number of different treatments in each design is then 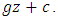 The “uncommon” treatments have
The “uncommon” treatments have 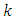 replications because uncommon treatments are limited to a particular Sudoku square design in an experimental environment and the common ones are replicated
replications because uncommon treatments are limited to a particular Sudoku square design in an experimental environment and the common ones are replicated 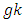 times that is,
times that is, 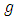 environments
environments 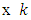 replications. We carry-out analysis of variance for each experiment in the usual way and obtained tests of significant and estimate of effects with errors has suggested by Gomes and Gumarie (1958). If the residual variance estimates are not significantly different a combined analysis can be carried out for the whole set of experiments.Sudoku square design assume that having
replications. We carry-out analysis of variance for each experiment in the usual way and obtained tests of significant and estimate of effects with errors has suggested by Gomes and Gumarie (1958). If the residual variance estimates are not significantly different a combined analysis can be carried out for the whole set of experiments.Sudoku square design assume that having 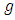 multi-environment experiments each with
multi-environment experiments each with 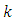 treatments, each occurs only once in each row, column or sub-block or square) such that
treatments, each occurs only once in each row, column or sub-block or square) such that 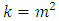 where
where 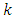 and
and 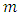 (number of row-block and column-block) are odd see (Subramani and Ponnuswamy 2009). If for example fig 1. is
(number of row-block and column-block) are odd see (Subramani and Ponnuswamy 2009). If for example fig 1. is 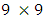 Latin square or
Latin square or 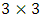 Sudoku square design. Considering the fig 1., the number of row-block and column-block is 3 which is an odd number.
Sudoku square design. Considering the fig 1., the number of row-block and column-block is 3 which is an odd number.
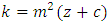 number of treatments is discussed.Model 1Hui-Dong and Rui-Gen (2008) proposed linear model for Sudoku square design and being modified to includes the multi-environment experiment as follows.
number of treatments is discussed.Model 1Hui-Dong and Rui-Gen (2008) proposed linear model for Sudoku square design and being modified to includes the multi-environment experiment as follows.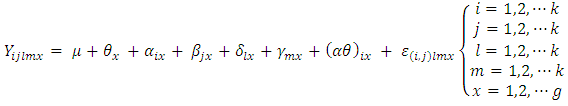
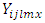 is a obseved value of the plot in the
is a obseved value of the plot in the 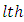 row and
row and 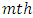 column, subjected to the
column, subjected to the 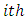 treatment,
treatment, 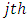 box of the
box of the 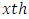 experimental environment;
experimental environment; 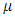 is the grand mean,
is the grand mean, 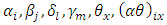 are the main effects of the
are the main effects of the 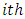 treatment,
treatment, 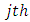 box,
box, 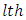 row,
row, 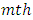 column,
column, 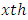 experimental environment and interaction between common treatments and environment respectively and
experimental environment and interaction between common treatments and environment respectively and 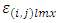 is the random error. Where SSEE is the sum of square of the experimental environment, SSt is the total treatment sum of square for all the multi-environment experiments, SSr is the total row sumof squres for all the multi-environment experiments, SSc the total column sumof squares for all the multi-environment experiments, SSs is the total sub-block sumof squares for all the multi-environment experiments, SSI is the total interaction sumof squares between common treatment and the multi-environment experiments and Sse the total error sumof squares for all the multi-environment experiments.If we let
is the random error. Where SSEE is the sum of square of the experimental environment, SSt is the total treatment sum of square for all the multi-environment experiments, SSr is the total row sumof squres for all the multi-environment experiments, SSc the total column sumof squares for all the multi-environment experiments, SSs is the total sub-block sumof squares for all the multi-environment experiments, SSI is the total interaction sumof squares between common treatment and the multi-environment experiments and Sse the total error sumof squares for all the multi-environment experiments.If we let 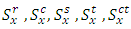 and
and 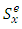 be the
be the 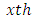 environment row, column, sub-square, treatment, common treatment and error sum of square respectively.
environment row, column, sub-square, treatment, common treatment and error sum of square respectively.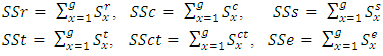 The alternative method of the above can be obtained as follows
The alternative method of the above can be obtained as follows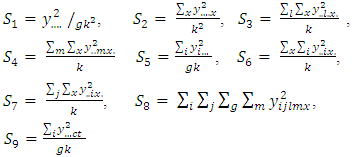 The computational analysis of the sum of the squares for the remaining models (2-5) are almost the same with model 1 and therefor not discussed in this paper for the detail computation analysis check Subramani and Ponnuswamy (2012) for separate analysis.
The computational analysis of the sum of the squares for the remaining models (2-5) are almost the same with model 1 and therefor not discussed in this paper for the detail computation analysis check Subramani and Ponnuswamy (2012) for separate analysis.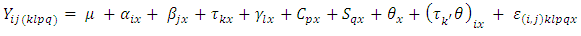
 and
and  Where
Where 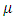 is general mean,
is general mean, 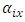 is
is 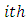 row-block effect in
row-block effect in 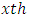 environmental experiment,
environmental experiment, 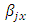 is
is 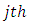 column-block effect in
column-block effect in 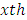 environmental experiment,
environmental experiment, 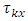 is
is 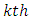 treatment effect in
treatment effect in 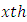 environmental experiment,
environmental experiment, 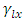 is the
is the 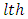 row effect in
row effect in 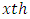 environmental experiment,
environmental experiment, 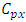 is
is 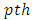 the column effect in
the column effect in 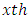 environmental experiment,
environmental experiment, 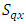 is the
is the 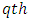 sub-square effect in
sub-square effect in 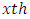 environmental experiment,
environmental experiment, 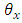 is the
is the 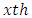 environmental experiment,
environmental experiment, 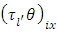 is the interaction between
is the interaction between 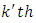 common treatment and
common treatment and 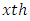 environmental experiment and
environmental experiment and 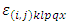 error component with mean zero and constant variance.
error component with mean zero and constant variance.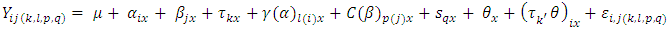
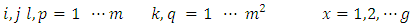 Where
Where 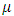 is general mean,
is general mean, 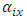 is
is 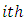 row-block effect in
row-block effect in 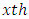 environmental experiment,
environmental experiment, 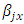 is
is 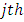 column-block effect in
column-block effect in 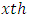 environmental experiment,
environmental experiment, 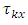 is
is 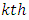 treatment effect in
treatment effect in 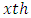 environmental experiment,
environmental experiment, 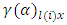 is the
is the 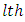 row effect nested in
row effect nested in 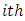 row-block in
row-block in 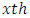 environmental experiment,
environmental experiment,  is the
is the 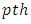 column effect in
column effect in 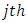 column-blockin
column-blockin 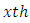 environmental experiment,
environmental experiment, 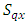 is the
is the 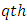 sub-square effect in
sub-square effect in 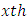 environmental experiment,
environmental experiment, 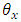 is the
is the 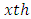 environmental experiment,
environmental experiment, 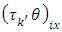 is the interaction between
is the interaction between 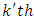 common treatment and
common treatment and 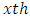 environmental experiment and
environmental experiment and 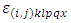 error component with mean zero and constant variance.
error component with mean zero and constant variance.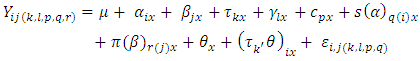
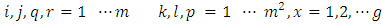 Where
Where 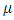 is general mean,
is general mean, 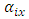 is
is 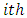 row-block effect in
row-block effect in 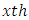 environmental experiment,
environmental experiment, 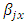 is
is 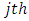 column-block effect in
column-block effect in 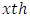 environmental experiment,
environmental experiment, 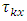 is
is 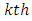 treatment effect in
treatment effect in 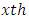 environmental experiment,
environmental experiment, 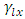 is the
is the 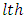 row effect in
row effect in 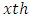 environmental experiment,
environmental experiment, 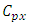 is
is 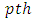 the column effect in
the column effect in 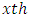 environmental experiment,
environmental experiment, 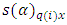 is the
is the 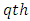 horizontal square effect nested in
horizontal square effect nested in 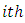 row-block in
row-block in 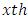 environmental experiment,
environmental experiment, 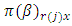 is the
is the 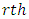 vertical square effect nested in
vertical square effect nested in 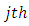 column-block in
column-block in 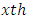 environmental experiment,
environmental experiment, 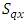 is the
is the 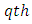 sub-square effect in
sub-square effect in 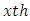 environmental experiment,
environmental experiment, 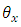 is the
is the 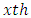 environmental experiment,
environmental experiment, 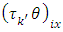 is the interaction between
is the interaction between 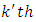 common treatment and
common treatment and 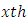 environmental experiment and
environmental experiment and 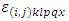 error component with mean zero and constant variance.Model 5: The modification of Type IV of Subramani & Ponnuswamy linear model is as follows. In the model below, it is assumed that the row effects and horizontal square effects are nested in the row block and the column effects and the vertical square effects are nested in the column block effect
error component with mean zero and constant variance.Model 5: The modification of Type IV of Subramani & Ponnuswamy linear model is as follows. In the model below, it is assumed that the row effects and horizontal square effects are nested in the row block and the column effects and the vertical square effects are nested in the column block effect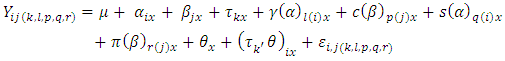
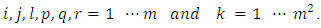 Where
Where 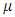 is general mean,
is general mean, 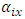 is
is 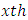 row-block effect in
row-block effect in 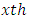 environmental experiment,
environmental experiment, 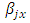 is
is 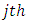 column-block effect in
column-block effect in 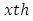 environmental experiment,
environmental experiment, 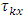 is
is 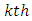 treatment effect in
treatment effect in 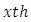 environmental experiment,
environmental experiment, 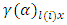 is the
is the 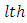 row effect nested in
row effect nested in 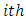 row-block in
row-block in 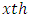 environmental experiment,
environmental experiment, 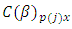 is the
is the 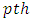 column effect in
column effect in 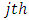 column-block in
column-block in 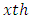 environmental experiment
environmental experiment 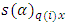 is the
is the 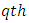 horizontal square effect nested in
horizontal square effect nested in 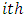 row-block in
row-block in 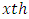 environmental experiment,
environmental experiment, 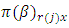 is the
is the 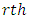 vertical square effect nested in
vertical square effect nested in 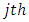 column-block in
column-block in 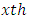 environmental experiment,
environmental experiment, 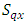 is the
is the 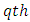 sub-square effect in
sub-square effect in 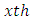 environmental experiment,
environmental experiment, 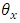 is the
is the 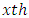 environmental experiment,
environmental experiment, 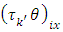 is the interaction between
is the interaction between 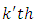 common treatment and
common treatment and 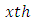 environmental experiment and
environmental experiment and 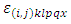 error component with mean zero and constant variance.
error component with mean zero and constant variance.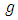 enviroments when treatments are not same in all experiments, but some treatments common in all the experiments. Five Sudoku design linear models were modified by adding environmental effects and interaction between common treatments and environmental effects terms to the models. The sum of square for rows, columns and sub-squares of
enviroments when treatments are not same in all experiments, but some treatments common in all the experiments. Five Sudoku design linear models were modified by adding environmental effects and interaction between common treatments and environmental effects terms to the models. The sum of square for rows, columns and sub-squares of 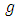 environments are obtained by summing all the individual sum of squares for rows, columns and sub-square respectively. Similarly, the same are done to obtain sum of squares for row-blocks, column-blocks, rows within row-block, column within column-block, horizontal square within row-block and vertical square within column-block respectively.
environments are obtained by summing all the individual sum of squares for rows, columns and sub-square respectively. Similarly, the same are done to obtain sum of squares for row-blocks, column-blocks, rows within row-block, column within column-block, horizontal square within row-block and vertical square within column-block respectively.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML



