-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Statistics and Applications
p-ISSN: 2168-5193 e-ISSN: 2168-5215
2016; 6(5): 300-308
doi:10.5923/j.statistics.20160605.04

Design Filtering and Reconstruction: A Procedure for Sequentially Locating D-Optimal Design Measures
Mary Paschal Iwundu
Department of Mathematics and Statistics, Faculty of Science, University of Port Harcourt, Choba, Nigeria
Correspondence to: Mary Paschal Iwundu, Department of Mathematics and Statistics, Faculty of Science, University of Port Harcourt, Choba, Nigeria.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The presence of non-optimal design points in an experimental design measure greatly affects the convergence of a search algorithm to a desired optimum. Filtering and reconstruction is presented as a viable procedure for sequentially locating D-optimal design measures. The method effectively improves experimental design in the search for an optimal design measure. While the procedure is identical to the Wynn’s sequential algorithm for constructing D-optimal designs, filtering and reconstruction addresses situations where outlying non-optimal design points had been admitted into the design possibly either by the creation of a poor initial design or by its influence on the next design point(s). By the method, outlying non-optimal design points are removed and the design reconstructed, thus resulting in a significant improvement on the determinant value of information matrix. Approximate solution has been obtained in the construction of D-optimal design measure for a two-dimensional non-interaction polynomial model defined on an irregular continuous design whose boundary is quadrilateral with vertices (2.2), (-1,1), (1,-1) and (-1,-1). Furthermore, bounds have been established for the determinant value of information matrix for each sequentially generated design. The bounds reveal that the D-optimal measure generated by the search procedure is very close to the true unknown D-optimal design measure.
Keywords: Filtering, Reconstruction, D-optimal, Sequential algorithm, Non-optimal points, Bounds
Cite this paper: Mary Paschal Iwundu, Design Filtering and Reconstruction: A Procedure for Sequentially Locating D-Optimal Design Measures, International Journal of Statistics and Applications, Vol. 6 No. 5, 2016, pp. 300-308. doi: 10.5923/j.statistics.20160605.04.
Article Outline
1. Introduction
- The consideration for construction of optimal design measures has gained top interests among researchers since from early works of Wynn (1970), Mitchell and Miller (1970), Fedorov (1972), Mitchell (1974), etc. In all practical terms, an optimal design enhances efficiency. Choosing an optimal experimental design for a full parameter regression, defined on a regular geometric area, has been given much attention. However difficulty arises with complexity of model or the design region or both. Sometimes it maybe needful to construct optimal designs for models that exist with improper polynomial regression functions and which may be defined on non-regular geometric areas. For whatever settings, the need for optimal designs cannot be played down. A documentary of the usefulness of optimum experimental design has been given by Atkinson (1996). Two very important and frequently used methods of constructing optimal designs are the sequential and exchange methods. Each of these methods has been in one or more of the early works mentioned above. Fundamental among them is the generation of D-optimal design measures. By definition, a design measure is a probability measure ξ defined on the design space
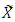 that is a closed compact set in a Euclidean space of a particular dimension. Moreover, ξ is a member of the set
that is a closed compact set in a Euclidean space of a particular dimension. Moreover, ξ is a member of the set 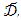 of all measures defined on the Borel Field
of all measures defined on the Borel Field 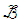 containing all one-point sets such that
containing all one-point sets such that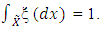 If
If 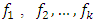 are
are 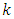 linearly independent functions defined on the design region
linearly independent functions defined on the design region 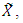 at each point
at each point 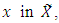 a random variable
a random variable 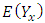 is defined and is such that
is defined and is such that 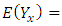
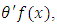 where
where 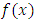 represents the kx1 column vector of functions
represents the kx1 column vector of functions 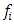 evaluated at
evaluated at 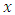 and
and 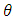 represents the kx1 column vector of unknown estimable parameters. For the measure
represents the kx1 column vector of unknown estimable parameters. For the measure 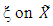
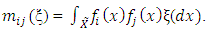 Letting
Letting 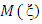 be the kxk information matrix whose
be the kxk information matrix whose 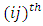 entry is
entry is 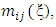 a discrete design measure may be formed by attaching a mass of
a discrete design measure may be formed by attaching a mass of 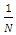 to each point of the discrete design such that
to each point of the discrete design such that 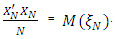 By discrete design measure, we refer to a design comprising of N points
By discrete design measure, we refer to a design comprising of N points 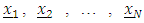 in
in 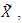 not necessarily distinct.A design measure
not necessarily distinct.A design measure 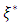 is said to be D-optimal if
is said to be D-optimal if 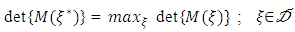 According to Kiefer and Wolfowitz (1960)
According to Kiefer and Wolfowitz (1960) 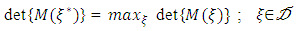 is equivalent to
is equivalent to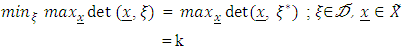 where k is the number of model parameters.Wynn (1970) presented an algorithm for locating D-optimal design measure. The sequential algorithm of Wynn constructs, as described by Labadi (2013), a converging sequence of discrete (exact) designs. Wynn’s algorithm is a procedure that could help in overcoming difficulties that may arise when the model or the design space is sufficiently complicated such as could prevent an immediate evaluation of an optimal design. The Wynn’s procedure simply sequentially adds a point of maximum variance of prediction to a given initial design. The process is continued till the design is brought closer to an optimal measure. The initial design point is admissible in the sense that the associated information matrix is nonsingular. Successive addition of design points to the initial design generates a sequence of designs which turn to the D-optimal design measure in the limit. Wynn’s method is a one point at a time method. A particular illustration was made using a two-dimensional non-interactive first-order polynomial model defined on an irregular design space whose boundary is quadrilateral with vertices (2.2), (-1,1), (1,-1) and (-1,-1). Since it is possible to have more than one point with maximum variance of prediction, there is a choice of an alternative point which maximizes the variance function. Under such settings, the particular sequence of designs generated will not be unique.Tsay (1976) gave a general procedure for the sequential construction of D-optimal designs, of which Wynn’s procedure is a special case. Robertazzi and Schwartz (1989) presented an accelerated sequential algorithm for producing D-optimal designs. The algorithm has a useful advantage when there is no prior information concerning the structure of the optimal design. An illustration using two dimensional regression function defined on a regular unit square was considered as well as an illustration using three dimensional regression function defined on a regular unit cube. Due to the likely existence of design locations at the interior of the design space, accelerated sequential method uses grid search having discrete grid approximations of a continuous space. In both illustrations, the number of function evaluations was greatly reduced. Hardin and Sloane (1993) presented a super algorithm which finds optimal or near optimal designs for a wide range of low order response surface problems involving large several variables of either the continuous or discrete types or both. Boon (2007) explored several techniques that could be used to numerically search for exact D-optimal designs. In his paper, several optimization algorithms for generating exact D-optimal design for any regression model were compared. Harman and Benková (2014) considered approximate D-optimal designs on varying experimental situations. Iwundu and Albert-Udochukwuka (2014) presented an efficient algorithm for constructing N-point D-optimal exact designs on regular as well as irregular design regions. Removing non-optimal support points in D-optimal design algorithms has been considered an effective way of speeding up algorithms for D-optimal design measures. Pronzota (2003) established a bound which helps to eliminate points from the design space during the search for a D-optimal design. Any point not satisfying the bound is removed from the design space and thus not considered for further investigation. Harman and Pronzota (2007) offered an improvement on the Pronzota (2003) lower bound on the maximum variance of prediction for an optimal point in the search for D-optimal design. Modifications of the very early algorithms continue to feature in current research works. Very recently, Al Labadi and Wang (2010) considered a two points at a time modification for the Wynn’s sequential algorithm for constructing D-optimal design. The modified algorithm adds to an initial design two points that have the same maximum variance of prediction. From the illustrative example of Al Labadi and Wang (2010) the modification achieved a reduction in the computational steps required to reach the D-optimal design by the Wynn’s algorithm roughly by one-half. It is obvious that the modification could address the non-uniqueness of the Wynn’s generated D-optimal sequence in the presence of only two maximum variance of prediction at each iteration. However, when there is no equal maximum variance of prediction, users of Al Labadi and Wang’s algorithm simply would return to the Wynn’s one-at-a-time sequential algorithm. Al Labadi (2013) considered the modification of the sequential algorithm and the exchange algorithm due to Fedorov (1972) by respectively, adding or exchanging two or more points at each iterative step of the original algorithm.In this work a refinement in the construction of D-optimal design using the Wynn’s basic sequential procedure is presented. It can be observed from the Wynn’s algorithm that in constructing D-optimal design, close attention should be paid to the variance of prediction as the determinant is not monotonically increasing at every phase or vicinity of the search. This point is worthy of note to avoid the error of reporting a false optimum when an improvement is not seen as reflected by the determinant value of information matrix at a current iteration. Understanding that D-optimality is achieved at the point where the variance of prediction approximately equals the number of model parameters is a more helpful rule of thumb for convergence to optimality. The attention however, is the construction of a D-optimal design measure for the two-dimensional no-interaction five parameter polynomial model
where k is the number of model parameters.Wynn (1970) presented an algorithm for locating D-optimal design measure. The sequential algorithm of Wynn constructs, as described by Labadi (2013), a converging sequence of discrete (exact) designs. Wynn’s algorithm is a procedure that could help in overcoming difficulties that may arise when the model or the design space is sufficiently complicated such as could prevent an immediate evaluation of an optimal design. The Wynn’s procedure simply sequentially adds a point of maximum variance of prediction to a given initial design. The process is continued till the design is brought closer to an optimal measure. The initial design point is admissible in the sense that the associated information matrix is nonsingular. Successive addition of design points to the initial design generates a sequence of designs which turn to the D-optimal design measure in the limit. Wynn’s method is a one point at a time method. A particular illustration was made using a two-dimensional non-interactive first-order polynomial model defined on an irregular design space whose boundary is quadrilateral with vertices (2.2), (-1,1), (1,-1) and (-1,-1). Since it is possible to have more than one point with maximum variance of prediction, there is a choice of an alternative point which maximizes the variance function. Under such settings, the particular sequence of designs generated will not be unique.Tsay (1976) gave a general procedure for the sequential construction of D-optimal designs, of which Wynn’s procedure is a special case. Robertazzi and Schwartz (1989) presented an accelerated sequential algorithm for producing D-optimal designs. The algorithm has a useful advantage when there is no prior information concerning the structure of the optimal design. An illustration using two dimensional regression function defined on a regular unit square was considered as well as an illustration using three dimensional regression function defined on a regular unit cube. Due to the likely existence of design locations at the interior of the design space, accelerated sequential method uses grid search having discrete grid approximations of a continuous space. In both illustrations, the number of function evaluations was greatly reduced. Hardin and Sloane (1993) presented a super algorithm which finds optimal or near optimal designs for a wide range of low order response surface problems involving large several variables of either the continuous or discrete types or both. Boon (2007) explored several techniques that could be used to numerically search for exact D-optimal designs. In his paper, several optimization algorithms for generating exact D-optimal design for any regression model were compared. Harman and Benková (2014) considered approximate D-optimal designs on varying experimental situations. Iwundu and Albert-Udochukwuka (2014) presented an efficient algorithm for constructing N-point D-optimal exact designs on regular as well as irregular design regions. Removing non-optimal support points in D-optimal design algorithms has been considered an effective way of speeding up algorithms for D-optimal design measures. Pronzota (2003) established a bound which helps to eliminate points from the design space during the search for a D-optimal design. Any point not satisfying the bound is removed from the design space and thus not considered for further investigation. Harman and Pronzota (2007) offered an improvement on the Pronzota (2003) lower bound on the maximum variance of prediction for an optimal point in the search for D-optimal design. Modifications of the very early algorithms continue to feature in current research works. Very recently, Al Labadi and Wang (2010) considered a two points at a time modification for the Wynn’s sequential algorithm for constructing D-optimal design. The modified algorithm adds to an initial design two points that have the same maximum variance of prediction. From the illustrative example of Al Labadi and Wang (2010) the modification achieved a reduction in the computational steps required to reach the D-optimal design by the Wynn’s algorithm roughly by one-half. It is obvious that the modification could address the non-uniqueness of the Wynn’s generated D-optimal sequence in the presence of only two maximum variance of prediction at each iteration. However, when there is no equal maximum variance of prediction, users of Al Labadi and Wang’s algorithm simply would return to the Wynn’s one-at-a-time sequential algorithm. Al Labadi (2013) considered the modification of the sequential algorithm and the exchange algorithm due to Fedorov (1972) by respectively, adding or exchanging two or more points at each iterative step of the original algorithm.In this work a refinement in the construction of D-optimal design using the Wynn’s basic sequential procedure is presented. It can be observed from the Wynn’s algorithm that in constructing D-optimal design, close attention should be paid to the variance of prediction as the determinant is not monotonically increasing at every phase or vicinity of the search. This point is worthy of note to avoid the error of reporting a false optimum when an improvement is not seen as reflected by the determinant value of information matrix at a current iteration. Understanding that D-optimality is achieved at the point where the variance of prediction approximately equals the number of model parameters is a more helpful rule of thumb for convergence to optimality. The attention however, is the construction of a D-optimal design measure for the two-dimensional no-interaction five parameter polynomial model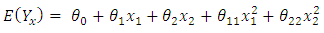 defined on an irregular and continuous space. Specifically, the design region is the irregular quadrilateral defined in Wynn (1970) and having a continuum of support points.
defined on an irregular and continuous space. Specifically, the design region is the irregular quadrilateral defined in Wynn (1970) and having a continuum of support points.2. Methodology
- As there is no information on the likely structure of the optimal design, discrete grid approximations to the continuous space shall be employed and search for the D-optimal design measure shall be within the discretized design space. The grid formations are as uniformly as possible, however due to the irregular nature of the design region, there are some grids that are not uniformly equi-spaced. The fundamental sequential search algorithm shall be based on the algorithm due to Wynn (1970). The search shall commence with an initial design whose design points need not necessarily be optimal points. The only requirement is that the initial design point be admissible in the sense that the associated information matrix of the design is nonsingular. It is clear that with the Wynn’s algorithm, having an initial design with non-optimal points would slow down the process for arriving at the optimal solution. To overcome this limitation, design filtering and reconstruction is proposed at some point in the sequence when cycles of optimal points are formed and it becomes clear which point(s) in the initial design are non-optimal points. By the filtering and reconstruction procedure, non-optimal points (unwanted and outlying points) are removed from the sequence of designs formed at earlier iterations and a replacement with optimal points made. The filtering and reconstruction procedure is supported by the method of experimental design reconstruction which according to Goupy (1996) is the most efficient way of detecting an outlier. The new procedure centers around handling non-optimal design points that were introduced possibly either by the creation of a poor initial design or by its influence on the next design point(s) added to the initial or existing design. As will be seen in section 3, removal of non-optimal design points will significantly improve the value of determent of information matrix at a next iteration. Moreover, the sequence will be certain to converge to the required D-optimal (or near) optimal design measure. Bounds shall be established for the determinant value of information matrix for each sequentially generated design.
3. Numerical Illustration
- To obtain a D-optimal design measure for the two-dimensional non-interaction polynomial model
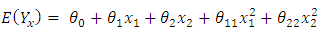 defined on the irregular continuous design space in Figure 1, whose boundary is quadrilateral with vertices (2.2), (-1,1), (1,-1) and (-1,-1), we discretize the region and obtain the candidate set
defined on the irregular continuous design space in Figure 1, whose boundary is quadrilateral with vertices (2.2), (-1,1), (1,-1) and (-1,-1), we discretize the region and obtain the candidate set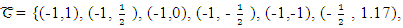
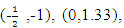
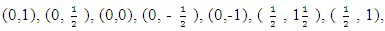
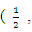
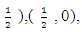
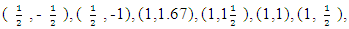
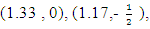
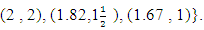
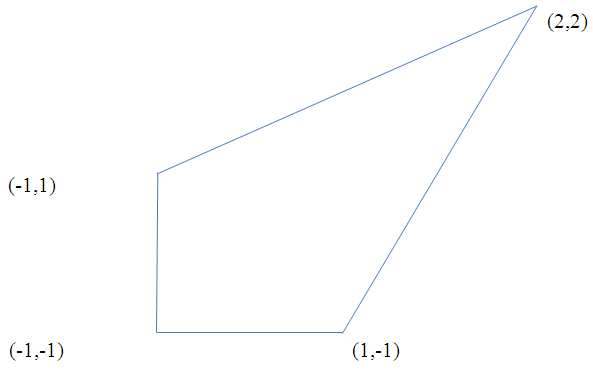 | Figure 1. Quadrilateral with vertices (2.2), (-1,1), (1,-1) and (-1,-1) |
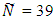 design points to be considered in the search for the D-optimal discrete design measure. The initial design is
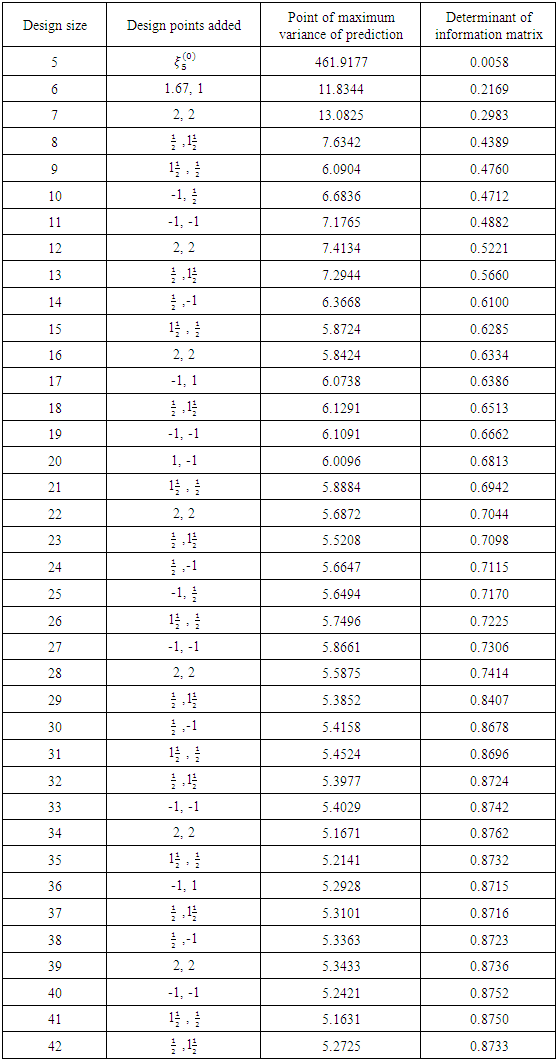
design points to be considered in the search for the D-optimal discrete design measure. The initial design is 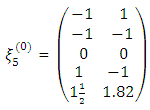 The generated sequence starting from the initial design yields the statistics in Table 1. The sequence is obtained by adding to the initial design the point of maximum variance of prediction. It is very clearly obvious that the sequence cycles around some design points of which the initial design points (0,0) and
The generated sequence starting from the initial design yields the statistics in Table 1. The sequence is obtained by adding to the initial design the point of maximum variance of prediction. It is very clearly obvious that the sequence cycles around some design points of which the initial design points (0,0) and 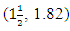 are not a part. Thus for N=29 the initial design is filtered and reconstructed by replacing the design points (0,0) and
are not a part. Thus for N=29 the initial design is filtered and reconstructed by replacing the design points (0,0) and 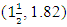 with (2, 2) and
with (2, 2) and 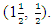 This greatly improved the determinant value from the supposed 0.7463 (without filtering and reconstruction) to 0.8407. There is also a replacement of the point (1.67, 1) with (-1, 1) at N=30. The point (1.67, 1) came into the design from the influence of poorly selected initial design. This replacement again allowed a maximal improvement in the determinant value of information matrix from the supposed 0.8414 to 0.8678. The MATLAB Version 2007b was employed in the generation of the sequence of the designs and the outputs are presented in Appendix A for N = 5, 6 and 7 only for space convenience.
This greatly improved the determinant value from the supposed 0.7463 (without filtering and reconstruction) to 0.8407. There is also a replacement of the point (1.67, 1) with (-1, 1) at N=30. The point (1.67, 1) came into the design from the influence of poorly selected initial design. This replacement again allowed a maximal improvement in the determinant value of information matrix from the supposed 0.8414 to 0.8678. The MATLAB Version 2007b was employed in the generation of the sequence of the designs and the outputs are presented in Appendix A for N = 5, 6 and 7 only for space convenience.
|
4. Discussion
- A refinement has been provided for a more effective use of the Wynn’s sequential algorithm in the construction of D-optimal design measure. The refinement addresses situations where non-optimal design points have been introduced into the search at an early stage of experimentation. The non-optimal design points may have been introduced possibly either by the creation of a poor initial design or by its influence on the next design point(s) added to the initial or existing design. Experimental designs in the presence of one or more non-optimal design points do not allow maximal possible improvement in the determinant value of information matrix at any iteration. Such non-optimal design points certainly do not reflect similar characteristics of the other points and hence are treated as unwanted or outlying design points of which Pronzota (2003) suggests should be removed from the design space and not considered for further experimentation.The filtering and reconstruction procedure allows a maximal improvement in the determinant value of information matrix. This is not surprising because an experimental design with non-optimal point(s) offers low determinant value of information matrix. By having points with similar characteristics in the design should yield a maximal improvement in the determinant value of information matrix.For the construction of D-optimal design measure for the two-dimensional no-interaction five parameter polynomial model defined on an irregular and continuous space, the algorithm converged at the design measure,
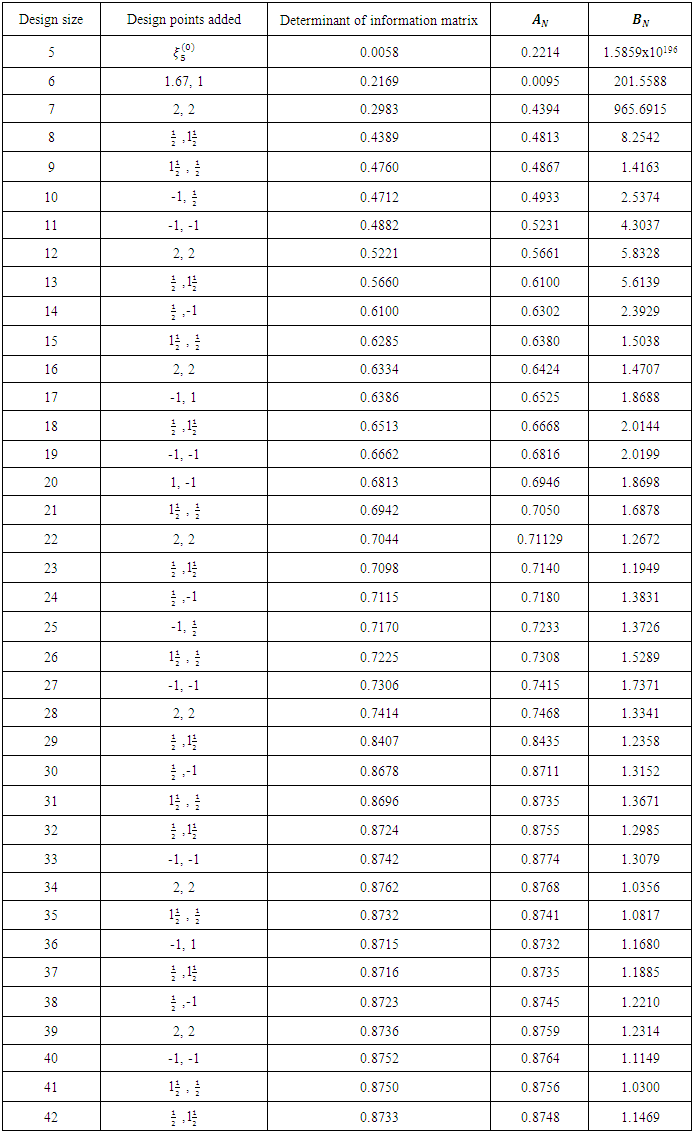
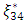 where the maximum variance of prediction was closest to the number of model parameters. There was no noticeable improvement in the determinant value of information matrix nor in the maximum variance of prediction two steps after N=34. The convergence to the D-optimal design measure was certain as N increased. Wynn’s mathematical justification supports this. Bounds for the determinants of information matrices associated with each design at each iterative step have been computed and are presented in Table 2. The bounds as established by Wynn (1970) are given by
where the maximum variance of prediction was closest to the number of model parameters. There was no noticeable improvement in the determinant value of information matrix nor in the maximum variance of prediction two steps after N=34. The convergence to the D-optimal design measure was certain as N increased. Wynn’s mathematical justification supports this. Bounds for the determinants of information matrices associated with each design at each iterative step have been computed and are presented in Table 2. The bounds as established by Wynn (1970) are given by 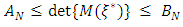 where
where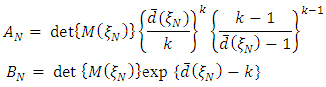
|
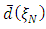 represents the maximum variance of prediction using the design measure,
represents the maximum variance of prediction using the design measure, 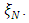 The bounds show how close the search is to the optimum design at any stage. From Table 2, the bounds
The bounds show how close the search is to the optimum design at any stage. From Table 2, the bounds 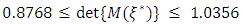 associated with the design
associated with the design 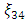 whose determinant value of information matrix is 0.8762, shows that
whose determinant value of information matrix is 0.8762, shows that 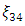 is very close to the true optimum design. The maximum determinant value of information matrix in the sequence generated is also associated with the design,
is very close to the true optimum design. The maximum determinant value of information matrix in the sequence generated is also associated with the design, 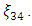 Furthermore, this design has a maximum variance of prediction approximately equal to k, the number of model parameters. For eight experimental runs after N=34 no significant improvement was seen in the search. On the basis of the grid search with the 39 grid points,
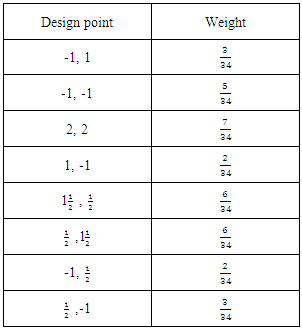
Furthermore, this design has a maximum variance of prediction approximately equal to k, the number of model parameters. For eight experimental runs after N=34 no significant improvement was seen in the search. On the basis of the grid search with the 39 grid points, 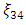 is thus reported as approximately D-optimal. The design measure is as in Figure 2. The associated information matrix is
is thus reported as approximately D-optimal. The design measure is as in Figure 2. The associated information matrix is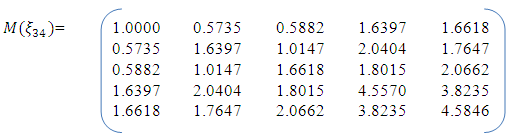
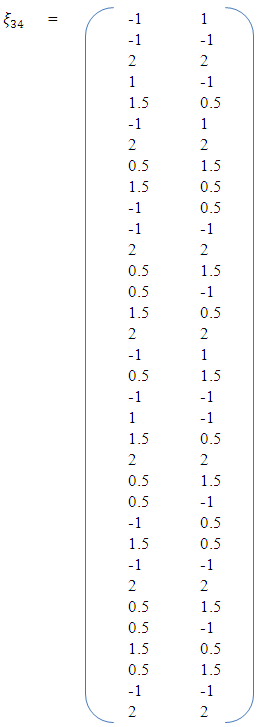 | Figure 2. 39 point approximately D-optimal design measure |
|
5. Conclusions
- A refinement in the construction of D-optimal designs using the Wynn’s basic sequential procedure has been presented. The refinement considers filtering and reconstruction as a viable procedure for sequentially locating D-optimal design measures. The method effectively improves experimental design in the search for an optimal design measure. While the procedure is identical to the Wynn’s sequential algorithm for constructing D-optimal designs, filtering and reconstruction addresses situations where outlying non-optimal design points had been admitted into the design possibly either by the creation of a poor initial design or by its influence on the next design point(s). By the method, outlying non-optimal design points are removed and the design reconstructed, thus resulting in a significant improvement on the determinant value of information matrix. In particular, an approximate solution has been obtained in the construction of D-optimal design measure for a two-dimensional non-interaction polynomial model defined on an irregular continuous design whose boundary is quadrilateral with vertices (2.2), (-1,1), (1,-1) and (-1,-1). Furthermore, bounds have been established for the determinant value of information matrix for each sequentially generated design. The bounds reveal that the D-optimal measure generated by the search procedure is very close to the true unknown D-optimal design measure.Although D-optimality criterion is determinant-based, it is important to pay close attention to the variance of prediction when constructing D-optimal designs. This is because the determinant of information matrix may not monotonically increase at every phase or vicinity of the search. Since D-optimality is achieved at the point where the variance of prediction approximately equals the number of model parameters, paying close attention to the variance of prediction becomes a helpful rule of thumb for convergence to optimality.
APPENDIX A
- MATLAB OUTPUT_ Design Filtering and Reconstruction Starting design
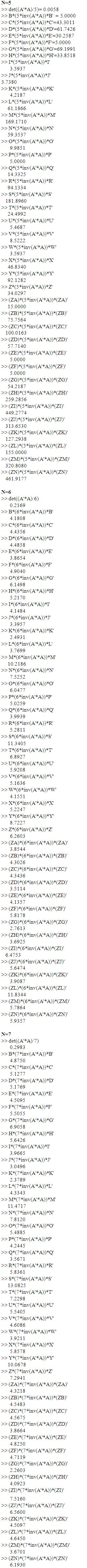
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML