1. Introduction

Maternal mortality as defined by the World Health Organization (WHO,1993) is the death of a woman whiles pregnant or within 42 days after termination of pregnancy, irrespective of the duration and site of the pregnancy, from any cause related to the pregnancy or its management but not from accidental or incidental cause. Maternal mortality continues to be a major public health problem despite many strategies devised by the international community to reduce it. Maternal mortality as a result is the leading cause of death among females aged 15-49 years mostly developing countries. According to the United Nations (UN, 2009) report, more than 1500 women die each day from pregnancy related causes resulting in an estimated figure of 550,000 maternal deaths annually.

Maternal mortality is unprobably high with about 830 women dying from pregnancy or childbirth related complications around the world every day. By the end of 2015, roughly 303,000 women will have died during and following pregnancy and childbirth. Almost all these deaths occurred in low resource settings, with 99 percent of all maternal death occurring in developing countries (WHO, 2015). The maternal mortality ratio (MMR) in developing countries in 2015 was 239 per 100,000 live births versus 12 per 100,000 live births in developed countries.

The leading causes of maternal mortality are mostly sub-grouped into direct and indirect causes. Direst causes of maternal mortality are those related to obstetric complications of pregnancy, labour and delivery and the post-partum periods. Direct causes of maternal mortality as revealed by previous researches conducted in Ghana includes haemorrhage, abortion, miscarriage, sepsis, obstructed labour, ectopic pregnancy, eclampsia and embolism (Mills, Williams, Wak and Hodgoson, 2008). Indirect causes of maternal mortality on the other hand are those relating to pre-existing medical conditions that may be aggravated by the physiologic demands of the pregnancy. The indirect causes of maternal mortality are often infectious and non-infectious diseases and other miscellaneous causes. According to the research conducted by Zakariah et al., (2009), malaria, HIV/AIDS, hepatitis, respiratory infections, anaemia, sickle cell diseases, meningitis, cerebrovascular disease and others are mainly the indirect causes of maternal mortality.

Between 2016 and 2030, as part of the Sustainable Development Agenda, the target is to reduce the global maternal mortality ratio to less than 70 per 100,000 live births. In view of this, it is hereby expedient that Ghana as a developing country provides the needed resources to ensure that this vision is realised. Based on this gap, this research will try to investigate the relationship between the direct major causes of maternal mortality and some indirect factors which includes age, parity and gravida using canonical correlation analysis.

2. Methodology

The purpose of this research work is to investigate the relationship between the direct major causes of maternal mortality and some indirect factors such as Age, Parity and Gravida. Data for the research work was a secondary historical maternal mortality data for the year 2007 through to 2012 compiled by Komfo Anokye Teaching Hospital (KATH). Komfo Anokye Teaching Hospital (KATH) was chosen with the reason being that, it is the second largest hospital in Ghana and the only tertiary health institution in Ashanti region. It was the main referral hospital for Ashanti, Brong Ahafo and the Northern regions of Ghana, until then Tamale Regional Hospital was upgraded to Teaching Hospital hence handling referrals from Northern, Upper East and Upper West regions thereby easing some pressure on Komfo Anokye Teaching Hospital. In view of this, Komfo Anokye Teaching Hospital (KATH) happens to be good center for data collection, since most referrals on serious cases including pregnancy related cases are sent there; which makes it a good place or location for sampling. A total of 1,015 maternal deaths within the age group of 12-49 years were analysed. The data were analysed using SPSS version 20.0. A canonical correlation analysis was employed to investigate the canonical correlation of two sets of variables by using SPSS. The analysis was conducted using direct major causes of maternal mortality which includes obstructed labour (ObtL), Haemorrhage (Hm), Unsafe Abortion (UnA), Eclampsia (Ecl), Ectopic pregnancy (Ecpreg), Embolism (Emb), Sepsis (Sep) and Anaesthesia (Anth) as the set of dependent set of variables (Y) and some Indirect factors such as Age (AGE), Parity (PAR) and Gravida (GRAV) as the set of independent variables (X). The canonical correlation analysis was performed to investigate the degree of relationship between the two sets of variables and to identify the most favourable linear combinations of the variable sets.

2.1. Canonical Correlation Analysis

Canonical correlation analysis was used to examine the relationship between two sets of variables that is the major direct causes of maternal mortality which is one set and another set of variables which includes age, parity and Gravida as indirect factors by using SYNTAX COMMAND procedure of SPSS.

Canonical correlation analysis focuses on the correlation between a linear combination of the variables in one set and a linear combination of variables in another set. A research conducted by Johnson and Wichern (1986) pointed out that, linear combinations of variables are useful for comparative purposes. According to Hair et al, (1998), the canonical covariates representing the optimal linear combinations of response and explanatory variables and canonical correlations showing the relationship between them are results of interest. Considering the equations below, it can be defined that 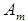and 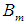are canonical variates obtained from each set of variables.

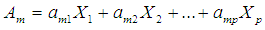(1)

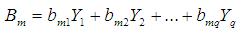(2)

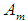The correlation between and 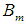can be called the canonical correlation (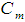). Squared canonical correlation (canonical roots) represents the amount of variance in canonical variates accounted for by the other canonical variates (Hair et al., 1998). The standardized coefficients are similar to the standardized regression coefficients in the multiple regressions that can be used as an indication of relative importance of the explanatory variables in determining the value of the response variable. Hence the aim of correlation analysis is to estimate the canonical coefficients; 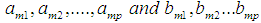when the canonical correlation is maximum.

A serial process can explain the maximization technique as follows;

Let the first group of 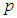variates be represented by the random vector, and let the second group of variates be represented by the random vector, 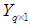. Thus for the random vectors X and Y, the population mean and (co)variance will be as follows;

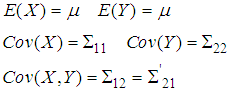Furthermore, X and Y random vectors and (co)variance can be written as follows;

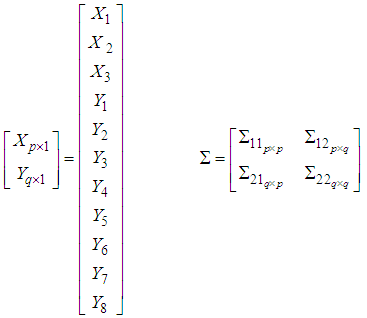So that the linear combination of the components of X and the components of Y will be as follows;

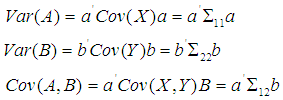The correlation coefficient between A and B is therefore formulated as;

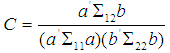(3)

2.2. Hypothesis for Assessing the Statistical Significance of the Canonical Correlation

The null and alternative hypothesis for assessing the statistical significance of the canonical correlation is;

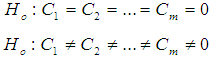In order to test the above hypothesis, the most widely used test statistic is the Wilki’s Lamda, which is given by the relation

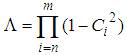(4)

3. Results

This section of the paper presents the results reported by the canonical correlation analysis.

3.1. Multivariate Test of Significance

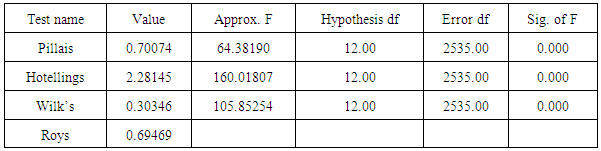
When performing a canonical correlation analysis, the first thing to do is to study the results from the multivariate test of significance. This test exhibits or shows whether the canonical model obtained is statistically significant or not. These test from the table 1 below includes Wilki’s Lamda, Pillais trace, Hotellings trace and Roy’s largest root but according to Sherry and Henson (2005) , authors generally chose to interpret their results on the basis of Wiki’s Lamda due to its higher level of practicality (Sherry and Henson, 2005). The findings from the multivariate test of significance table below collectively indicates that, the full model across all functions is statistically significant using the Wilk’s λ =0.30346 criterion, with F = (12,2535.00) = 105.85254, p<0.000. Because the Wiki’s λ represents the unexplained variance by the model, 1-λ yields the full canonical model effect size that is 1-λ represents the amount of variance shared by the canonical variables. Hence for the three (3) canonical functions, the effect size is 0.69654, which indicates that, the full model explained a substantial portion, about 70% of the variance shared between the two variable sets (direct major causes of maternal mortality and some indirect factors).

Table 1. Multivariate Test of Significance

3.2. Eigenvalues and Canonical Correlations

Table 2 below presents both the eigenvalues of the canonical functions and their correlation values. The eigenvalues concerning the canonical functions and canonical correlation values are used to decide which of the canonical functions has the maximum correlation and also significant (Sherry and Henson, 2005). From the table above, it can be observed under the Root No. column that, three (3) canonical function were derived from the canonical correlation analysis. The canonical correlation for the first canonical function from the table 2 is 0.83348 indicating the amount of shared variance between the first and second data sets in the first function is 69.469 percent. The second canonical correlation function also gave a canonical correlation value of 0.007446 indicating the amount of shared variance between the first and second data set in the second function is 0.555percent. The third canonical correlation function exhibited the maximum correlation between the minimum correlation between the three (3) canonical functions unaccounted for by the first and second canonical functions. This value of third canonical function from table 2 is 0.0224 suggesting that, the amount of variance shared between the two data sets in the third function is 0.050%. This analysis as a result points out that the first canonical function has the maximum correlation and also significant since it explains the largest amount of variance shared between the two data sets.

Table 2. Eigenvalues and Canonical Correlations

3.3. Dimension Reduction Analysis

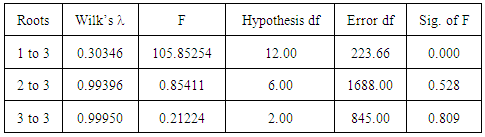
A canonical correlation analysis includes a dimension reduction analysis which is used to identify the extent to which each canonical function is able to account for shared variance between the data sets and also allows the researcher to test the hierarchical arrangements of functions for statistical significance.

As noted from the dimension reduction analysis table below, the full model (function 1-3) is statistically significant with F(12.00,233.66)=105.85254, p=0.000<0.05. It can be observed from the same table that function 2 to 3 and function 3 did not explain a statistically significant amount of shared variance between the variable sets hence insignificant with F(6.00,1688.00)=0.85411, p=0.528>0.05 and F(2.00,845.00)=0.21224, p=0.809>0.05 respectively.

Table 3. Dimension Reduction Analysis

3.4. Canonical Analysis for the First Canonical Function Concerning the Correlation between the Major Direct Causes of Maternal Mortality and Some Indirect Factors (Age, Parity and Gravida)

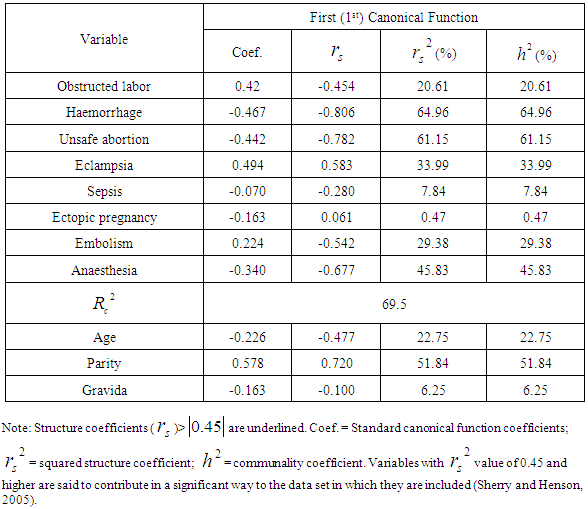
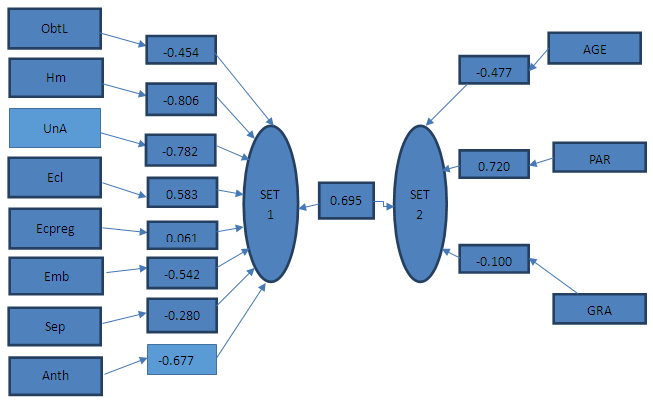
Given the 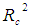(Canonical Correlation square) effect for each function, only the first canonical function was considered noteworthy in the context of the analysis since it explained a substantial amount of shared variance (69.5%). The last two canonical functions only explained 0.6 percent and 0.05percent respectively of the remaining variance in the variable sets after the extraction of the prior function (refer table 2). Hence a canonical correlation analysis for only the first canonical function concerning the correlation between the two sets of variables with respect to maternal mortality is created since the amount of variance explained by the first function is more impressive as compared to the last two functions that Function 2 and Function 3.

In order to know the extent to which the variables included in the data contributes to the correlation between the canonical variables, the standardized coefficients and structural coefficients regarding the canonical functions are used. This analysis indicated in the table 4 below includes the evaluation of the standardized coefficients and structural coefficients of the first canonical function.

Looking at the coefficients of the first function from the table 4 below, it can be observed that the relevant (significant) variables among the direct major causes of maternal mortality are primarily haemorrhage, unsafe abortion and anaesthesia with embolism and obstructed labor being the secondary contributions to the direct causes of maternal mortality. This is as a result supported by the squared structure coefficients .

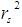It can also be deduced from the table 4 below that, with the exception of the variable eclampsia, all the other relevant variables (major direct causes of maternal mortality) have structure coefficients with the same sign, indicating they are all positively related to the predictor variables (age, parity and gravida).

Table 4. Canonical Analysis for the First Canonical Function concerning the Correlation between Major Direct Causes of Maternal Mortality and Some Indirect Factors (Age, Parity and Gravida)

With respect to the predictor variables (age, parity and gravida), which represents the second set of variables in the first canonical function, parity was the primary contributor to maternal mortality with secondary contribution by age based on their respective structure coefficients being greater than 45 percent. Again from the table 4, it can be noted that the structure coefficient of the variable Parity is positive (0.720) indicating that Parity is negatively related to all the direct major causes of maternal mortality with the exception of eclampsia; meaning Parity is positively related to eclampsia. Age also on the other hand had a negative structural coefficient value of -0.477 indicating it is positively related to all the major direct causes of maternal mortality with the exception of Eclampsia since its structural coefficient is negative.

Figure 1. Structure Coefficients and Canonical Correlation Value for the First Canonical Function concerning the Correlation between Direct Major Causes of Maternal Mortality and some Indirect Factors (Age, Parity and Gravida)

4. Discussion and Conclusions

This present paper is a study on the correlation between the direct major causes of maternal mortality and some indirect factors (Age, Parity and Gravida) through a canonical correlation analysis. The canonical correlation analysis was carried out using eight (8) variables as direct major causes of maternal mortality and three (3) variables as indirect factors contributing to maternal mortality to evaluate the multivariate shared relationship between the two sets of variables. The results of the canonical correlation analysis have revealed there is a significant relationship between the direct major causes and the indirect factors of maternal mortality. The analysis yielded three (3) canonical functions with squared canonical correlation (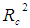) of 0.69469, 0.0055 and 0.00050 for each successive function. Collectively, the full model across all functions was statistically significant using Wilk’s (λ) = 0.30346 criterion, with F(12, 2535.00)=105.85254, p<0.000. Because the Wilk’s (λ) represents the variance unexplained by the model, 1-λ yields the full model effect size in the r² metric. Hence for the set of three (3) canonical functions, the r² type of effect size was 0.69654, which indicates that the full model explained a substantial portion, about 69.7% of the variance shared between the variable sets.

The dimension reduction analysis on the other hand allows the researcher to test the hierarchical arrangement of functions for statistical significance. As noted from table 3, the full model (function 1-3) was statistically significant. functions 2 to 3 and function 3 did not explain a statistically significant amount of shared variance between the variable sets. Given 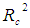effects for each function, only the first function was considered noteworthy or significant in the context of this research (69.5% of the shared variance). The last two functions only explained 0.56% and 0.050% respectively of the remaining amount of variance in the variable sets after the extraction of the prior function.

Table 4 on also presented the standardized function coefficients and structure coefficients for the first canonical function. After looking at the function coefficients, it was observed that, the relevant variables among the major direct causes of maternal mortality were primarily haemorrhage, unsafe abortion and anaesthesia with embolism and obstructed labor making the secondary contribution with respect to the causes of maternal mortality. Furthermore, with the exception of eclampsia, all the other relevant direct major causes of maternal mortality variables had their structure coefficients with the same sign which as a result indicted that they are all positively related. Regarding the predictor variable set in the first canonical function, Parity was the only primary contributor to maternal mortality with the secondary contribution by Age. Because Parity had a positive structure coefficient, it was negatively related to all the direct major causes of maternal mortality except eclampsia. Age was also positively related to the direct major causes of maternal mortality with the exception of eclampsia since it had a negative structural coefficient in the first canonical function.