1. Introduction

In a linear regression model there are situations where the regressors may be correlated and the error terms may be autocorrelated. This phenomenon is known as autocorrelated model with multi collinearity. It is well known that when there is multicollinearity, the ordinary least square (OLS) estimator for regression coefficients or the predictor based on these estimates may give poor results [1]. For overcoming the problem of multicollinearity several methods are available such as Principal component regression, Ridge regression and Partial least squares. These methods are useful when the errors are non autocorrelated. But in the presence of autocorrelated model with multicollinearity, appropriate modifications needs to be incorporated in the estimation. Accordingly a new estimator called generalized ridge estimator is proposed and its performance is compared with Ordinary ridge estimator. Ridge estimator involves unknown ridge parameter. In the literature several methods have been discussed for the choice of ridge parameter. Simulation study has been carried out to find the appropriate method for estimating the ridge parameter which gives minimum MSE for the proposed ridge estimator.

2. Materials and Methods

Consider the multiple linear regression model

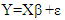(1)

where Y is an observational vector of dimension n x 1, X is a n x p data matrix of regressors, β is a p x 1 vector of regression coefficient and ε is a n x 1 disturbance vector. Under the assumption that X is full rank, the errors are non autocorrelated and X and ε are independently distributed, the Ordinary Least Square (OLS) estimator of β is

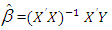with the covariance matrix of 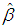is obtained as .

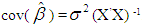It is not necessary that assumptions mentioned above hold good in real life situation. The regressors may be nearly correlated and the responses may also be correlated. In such instances the OLS estimator mentioned above do not possess the optimum statistical property. Hence there is a need to develop a new estimator which takes care of this situation.

Ridge Regression: The violation of the assumption of independent regressors leads to multicollinearity. If X is less than full rank then such a situation is known as perfect multicollinearity. In this case OLS estimator does not exist. This situation is very rare in practice. In most of the real life situations, some regressors are nearly related to the remainining regressors. This is known as near multicollinearity. In case of near multicollinearity, rank of the regressor matrix X is equal to k and hence OLS estimator exist, but they are too imprecise to be of much use [2]. With strongly interrelated pairs of regressors, X’X is illconditioned and the variance of the OLS estimator becomes large. With multicollinearity, the estimated OLS coefficients may be statistically insignificant (too large, too small and even have wrong sign). Hence interpretation given to the regression coefficients may no longer be valid. It may be preferable to consider biased estimators of β, if their variances are sufficiently smaller than those of OLS estimators. One such biased estimator is the “ridge estimator”. The ridge estimator (ordinary ridge estimator) of β is

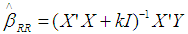(2)

where the constant k >0 is known as “ridge” parameter . As the constant k increases from zero and continues up to infinity, the regression estimates tend towards zero. Though these estimators result in biased estimates, for certain positive values of k, this estimator yields minimum mean squared error (MMSE) compared to OLS. Several methods for estimating k has been proposed by Hoerl and Kennard [3], Hoerl et al., [4], Mc Donald and Galarneau [5], Hocking et al., [6], Saleh and Kibria [7], Khalf and Shukur [8]. 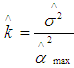From example Hoerl and Kennard (1970), the value of k that minimises the MSE is , where 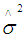represents the error variance of model (1), 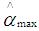is the maximum among elements of 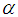defined as 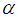=D^’β with D being an orthogonal matrix.

Autocorrelation: Autocorrelation is said to exist when the successive observations in linear regression model are correlated. The existence of autocorrelated errors has been rationalized in a variety of ways, as noted by Maddala [9].

The successive dependence of the error term is represented by

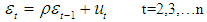(3)

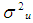u_t are independent and identically distributed random variable with mean zero and variance [10]. When the error satisfies the relation (3), the observations follow first order autocorrelation. The variance covariance matrix of Y is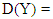

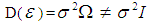Where 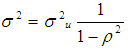and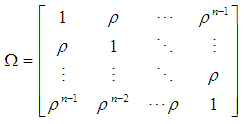

Since the covariance matrix of ε is nonspherical (i.e not a scalar multiple of the identity matrix), OLS, though unbiased, is inefficient relative to generalised least squares by Aitken’s theorem. The generalized least squares estimator of β in (1) is [10]

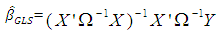(4)

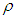If the parameter in (3) is known then we can write

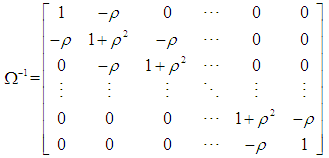(5)

3. Generalised Ridge Type Estimator

Consider a general linear regressive model (1) with errors satisfying relation (3) and the regressors exhibiting near multicollinearity. As seen earlier, in case of autocorrelation 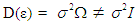. Hence autocorrelation is a particular case of heteroscedasticity. In the case of heteroscedasticity, GLS is an appropriate method of estimation as given in (4). Further, when there is multicollinearity, often used method is the ridge regression as mentioned in (2). Combining these two methods, we propose for the autocorrelated model with multicollinearity a generalized ridge type estimator represented as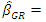 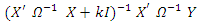where 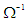is as defined in (5).

Hence the model under consideration contains the unknown parameters k, 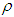, 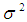and β.

In the following [11] we present some existing methods for estimating ridge parameter k

1. Hoerl and Kennard method

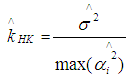(6)

2. Hoerl, Kennard and Baldwin method

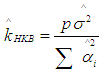(7)

3. Hocking, Speed and Lynn method

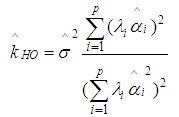(8)

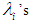For the proposed estimator, are the eigen values of .

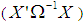4. The Monte Carlo Simulation Study

A simulation study is carried out to find out the appropriate estimate for the ridge parameter among (6), (7), (8) mentioned above which gives minimum MSE for the proposed estimator.

The data is simulated in accordance with the multiple linear regression model given in (1) with the number of regressors p=3 and ε satisfying first order auto regressive scheme as mentioned in (3). The dependent variable Y is generated using the relation Y=Xβ +ε with 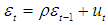X=[ X₀ , X₁ , X₂ , X₃ ], β=[ β₀ β₁ β₂ β₃ ]’ =[4 2.5 1.8 0.6]’, X₀ =[1 1 1….1]’.

To generate normally distributed random variables X₁, X₂, X₃ with specified intercorrelations we use the following equations [12, 13].

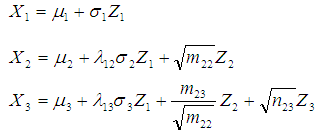where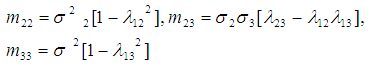

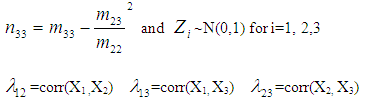In equation (3), u_t are independent and identically distributed normal random variables with mean 0 and variance 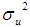. The autocorrelation coefficient 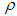in (3) is ranging from -0.9 to -0.1 and the regression parameters are fixed as ,.

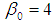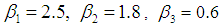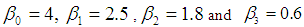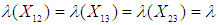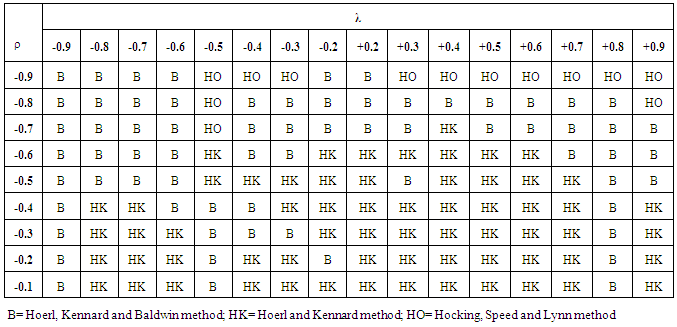
The parameters of the model in equation (4) are fixed as . Taking sixteen different levels of intercorrelation (multicollinearity) among the regressors are taken as -0.2, -0.3, -0.4, -0.5, -0.6, -0.7, -0.8, -0.9, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9.

With the above setup a sample of 100 observations are generated and replicated 1000 times. For each choice of the k, the MSE for the generalized ridge estimator is computed. The estimator of the ridge parameter (k) which gives minimum MSE is recorded for different choice of the parameters 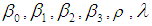and the results are presented in Table 1.

5. Results and Discussions of the Simulation Study

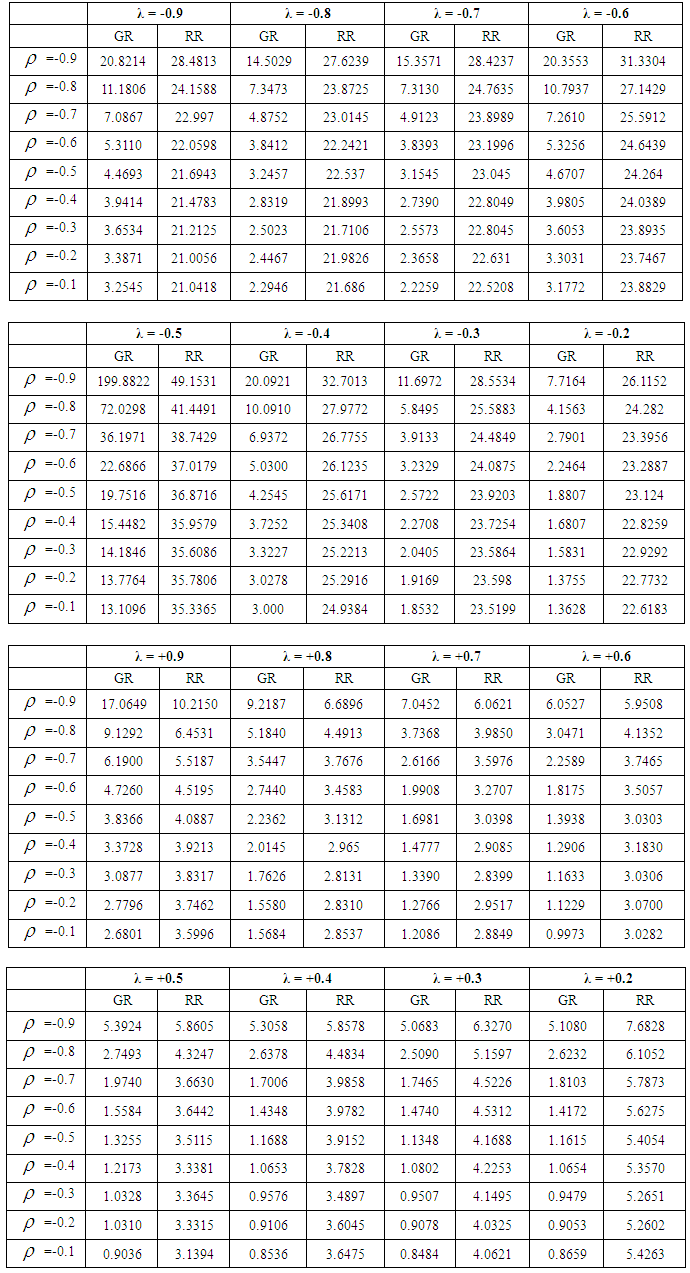
The first column of Table 1 contains 9 levels of autocorrelation and the first row represents different levels of intercorrelation between the regressors. The other elements in Table 1 represents the choice of the ridge parameter which gives minimum MSE for the proposed generalized ridge estimator. For example, ρ = -0.3 and λ =+0.2, Hoerl and Kennard (HK) estimator of the ridge parameter gives minimum MSE. Similarly when ρ = -0.7 and λ = -0.2, Hoerl Kennard and Baldwin (B) estimator of the ridge parameter gives minimum MSE.

From the results in Table 1, it is clear that when ρ and λ are negative and very high, the estimator for k proposed by Baldwin et al possesses minimum MSE. For the same values of λ, when autocorrelation is low, Hoerl and Kennard (HK) estimator is superior to Hoerl Kennard and Baldwin(B)estimator. Also as multicollinearity is positive and increases with the autocorrelation being low, then it is observed that Hoerl and Kennard (HK) estimator performs better than the other estimators.

When the intercorrelation among regressors is high and autocorrelation is also high, the ridge parameter proposed by Hoerl Kennard and Baldwin (B) is superior compared to the other estimates. Hence using (B) estimator, the proposed generalized ridge estimator (GR) is compared with Ordinary ridge estimator (RR) through MSE. Table 2 gives the MSE of GR estimator and RR estimator for different choice of λ and ρ.

The results in Table 2, depicts that developed Generalised ridge estimator (GR) has minimum MSE compared to Ordinary ridge (RR) estimator. Therefore in the presence of autocorrelation with multicollinearity the proposed ridge estimator is superior to ordinary ridge estimator. Hence use of ordinary ridge estimator leads to larger MSE if autocorrelation is ignored.

Table 1. Performance of the Proposed Estimator when p=3 for Different Choice of Ridge parameter, Different Levels of Correlation Between the Regressors ( λ ) and the Autocorrelation (ρ) Ranging from -0.9 to -0.1

Table 2. Comparison of the Proposed Generalised Ridge Estimator (GR) with Ordinary Ridge Estimator (RR) for Different Levels of Autocorrelation and Inter Correlations between the Regressors

6. Conclusions

There are a number of articles where multicollinearity and autocorrelation are dealt separately. However limited studies are available which describes these two problems together. Hence in this article, an attempt has been made to address these 2 issues. It is observed through simulation that the use of ordinary ridge estimator leads to larger MSE if autocorrelation is ignored.

Therefore while conducting research in the field of Social Sciences or Epidemiological studies, there is a critical need to check data for the existence of multicollinearity between the regressors as well as the presence of autocorrelation. This will avoid misinterpretation of the results and will also ensure that the emerging problems involving the inter relationships between a number of variables of interest may be addressed appropriately and effectively.

ACKNOWLEDGEMENTS

The authors are grateful to the reviewers for their valuable suggestions.