-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Statistics and Applications
p-ISSN: 2168-5193 e-ISSN: 2168-5215
2015; 5(6): 338-348
doi:10.5923/j.statistics.20150506.08

Shanker Distribution and Its Applications
Rama Shanker
Department of Statistics, Eritrea Institute of Technology, Asmara, Eritrea
Correspondence to: Rama Shanker, Department of Statistics, Eritrea Institute of Technology, Asmara, Eritrea.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper a new one parameter lifetime distribution named “Shanker distribution” for modeling lifetime data has been suggested. Various mathematical properties of the new distribution including its shape, moments, generating functions, hazard rate and mean residual life functions, stochastic ordering, order statistics, Renyi entropy measure, mean deviations, Bonferroni and Lorenz curves, and stress-strength reliability have been presented. The conditions of over-dispersion, equi-dispersion, and under-dispersion of Shanker distribution have been discussed. The method of maximum likelihood estimation and the method of moments have been discussed for estimating its parameter. The usefulness, applicability and superiority of the proposed distribution over exponential and Lindley distributions have been illustrated with three real lifetime data- sets.
Keywords: Moments, Hazard rate function, Mean residual life function, Mean deviations, Order statistics, Stress-strength reliability, Estimation of parameter, Goodness of fit
Cite this paper: Rama Shanker, Shanker Distribution and Its Applications, International Journal of Statistics and Applications, Vol. 5 No. 6, 2015, pp. 338-348. doi: 10.5923/j.statistics.20150506.08.
Article Outline
1. Introduction
- A number of continuous distributions for modeling lifetime data such as exponential, Lindley, gamma, lognormal, and Weibull are available in statistical literature. The exponential, Lindley and the Weibull distributions are more popular than the gamma and the lognormal distributions for modeling lifetime data-sets because the survival functions of the gamma and the lognormal distributions cannot be expressed in closed forms and both require numerical integration. Though each of exponential and Lindley distributions has one parameter, the Lindley distribution has one advantage over the exponential distribution that the exponential distribution has constant hazard rate whereas the Lindley distribution has monotonically decreasing hazard rate.Lindley distribution, introduced in the context of Bayesian analysis as a counter example of fiducial statistics, having its probability density function (p.d.f.) and cumulative distribution function (c.d.f.)
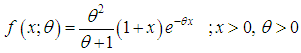 | (1.1) |
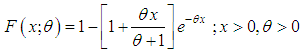 | (1.2) |
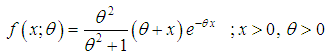 | (1.3) |
 and gamma
and gamma 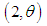 distributions as follows:
distributions as follows: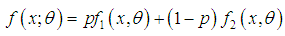 | (1.4) |
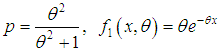 and
and 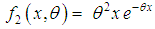 .The first derivative of (1.3) is obtained as
.The first derivative of (1.3) is obtained as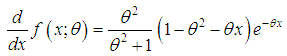 Thus
Thus 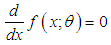 gives
gives 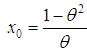 . From this it follows that (i) for
. From this it follows that (i) for  ,
,  implies that
implies that 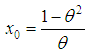 is the unique critical point at which
is the unique critical point at which 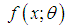 is maximized.(ii) for
is maximized.(ii) for 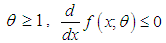 implies that
implies that 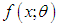 is decreasing in
is decreasing in 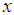 .Therefore, the mode of the distribution (1.3) is given by
.Therefore, the mode of the distribution (1.3) is given by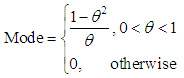 | (1.5) |
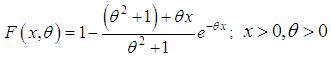 | (1.6) |
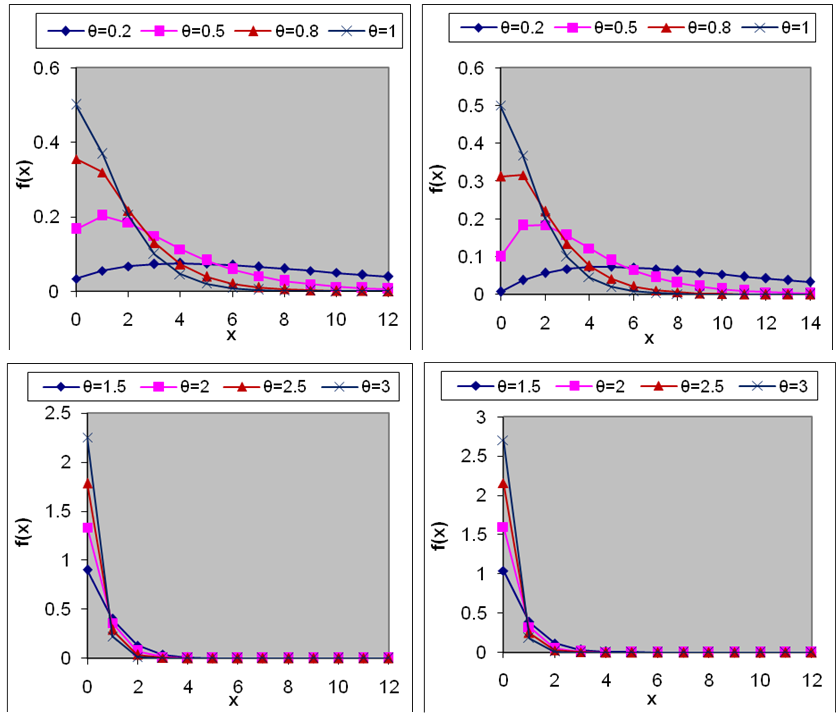
 are shown in figures 1 and 2.
are shown in figures 1 and 2.2. Moments and Associated Measures
- The
 the moment about origin of Shanker distributon (1.3) has been obtained as
the moment about origin of Shanker distributon (1.3) has been obtained as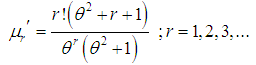 and so the first four moments about origin as
and so the first four moments about origin as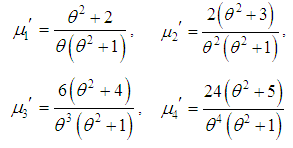 Thus the moments about mean of the Shanker distribution are as follows
Thus the moments about mean of the Shanker distribution are as follows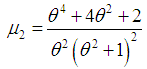
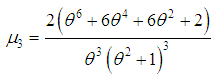
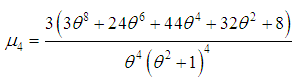 The coefficient of variation
The coefficient of variation 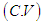 , coefficient of skewness
, coefficient of skewness 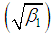 , coefficient of kurtosis
, coefficient of kurtosis 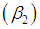 and Index of dispersion
and Index of dispersion 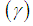 of Shanker distribution are thus obtained as
of Shanker distribution are thus obtained as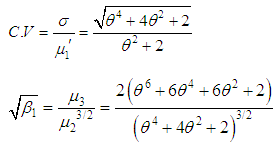
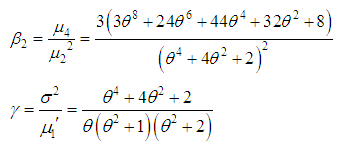 It can be easily shown that Shanker distribution is over-dispersed
It can be easily shown that Shanker distribution is over-dispersed 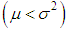 , equi-dispersed
, equi-dispersed 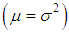 and under-dispersed
and under-dispersed 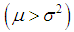 for
for 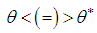
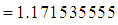 . It would be recalled that Lindley distribution is over-dispersed
. It would be recalled that Lindley distribution is over-dispersed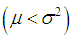 , equi-dispersed
, equi-dispersed 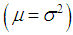 and under-dispersed
and under-dispersed 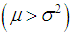 for
for 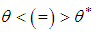
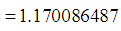 while exponential distribution is over-dispersed
while exponential distribution is over-dispersed 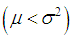 , equi-dispersed
, equi-dispersed 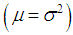 and under-dispersed
and under-dispersed 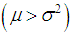 for
for 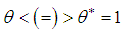 .
.3. Generating Functions
- The moment generating function
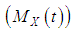 , characteristic function
, characteristic function 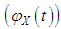 , and cumulant generating function
, and cumulant generating function 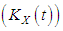 of Shanker distribution (1.3) are given by
of Shanker distribution (1.3) are given by 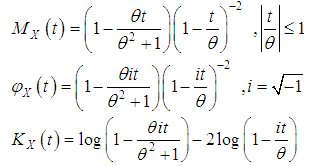 Using the expansion
Using the expansion 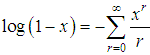 , we get
, we get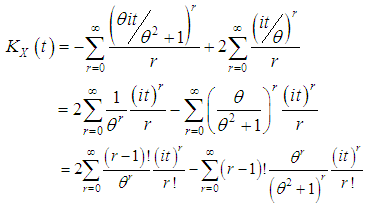 Thus the
Thus the  th cumulant of Shanker distribution is given by
th cumulant of Shanker distribution is given by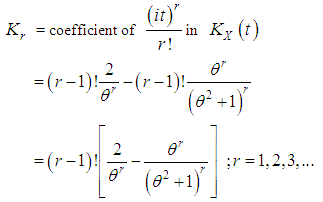 This gives
This gives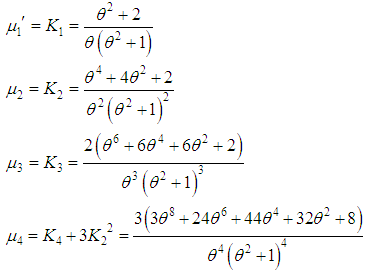 which are the same as obtained earlier.
which are the same as obtained earlier.4. Hazard Rate and Mean Residual Life Functions
- Let
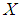 be a continuous random variable with p.d.f.
be a continuous random variable with p.d.f. 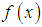 and c.d.f.
and c.d.f. 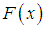 . The hazard rate function (also known as the failure rate function) and the mean residual life function of
. The hazard rate function (also known as the failure rate function) and the mean residual life function of 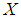 are respectively defined as
are respectively defined as 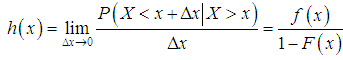 | (4.1) |
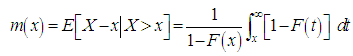 | (4.2) |
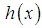 and the mean residual life function,
and the mean residual life function, 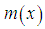 of Lindley distribution are given by
of Lindley distribution are given by  | (4.3) |
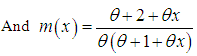 | (4.4) |
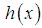 and the mean residual life function,
and the mean residual life function, 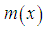 of the Shanker distribution are obtained as
of the Shanker distribution are obtained as 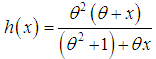 | (4.5) |
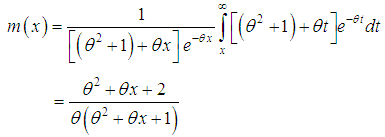 | (4.6) |
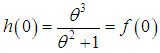 and
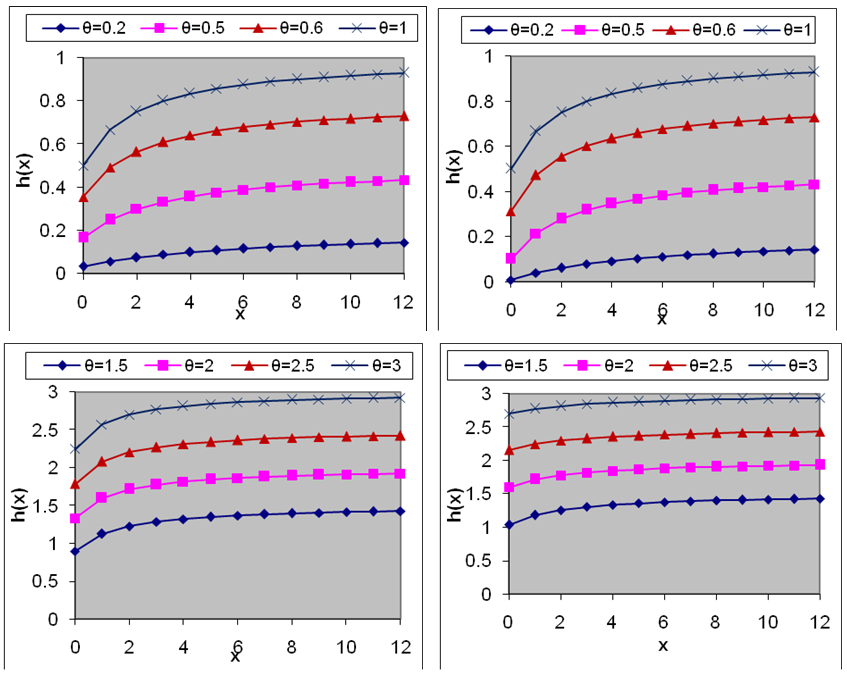
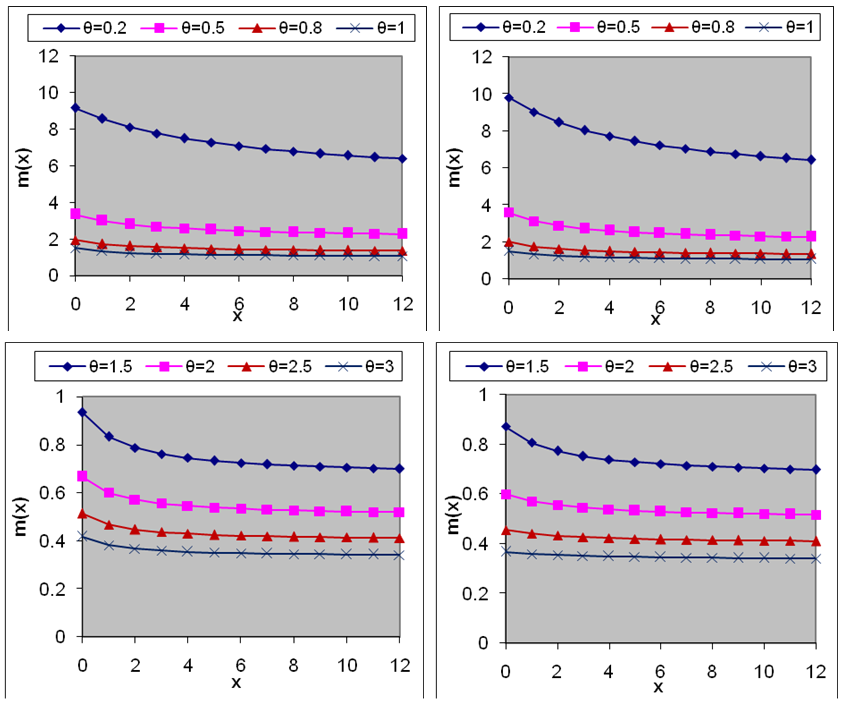
and 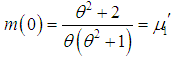 . It is also obvious from the graphs of
. It is also obvious from the graphs of 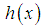 and
and 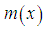 that
that 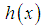 is an increasing function of
is an increasing function of 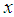 , and
, and 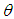 , whereas
, whereas 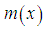 is a decreasing function of
is a decreasing function of 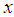 , and
, and 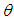 . The hazard rate function and the mean residual life function of the Shanker distribution show its flexibility over exponential and Lindley distributions. The graphs of the hazard rate function and mean residual life function of Lindley and Shanker distributions are shown in figures 3 and 4.
. The hazard rate function and the mean residual life function of the Shanker distribution show its flexibility over exponential and Lindley distributions. The graphs of the hazard rate function and mean residual life function of Lindley and Shanker distributions are shown in figures 3 and 4.5. Stochastic Orderings
- The stochastic ordering of positive continuous random variables is an important tool for judging their comparative behavior. A random variable
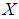 is said to be smaller than a random variable
is said to be smaller than a random variable 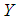 in the (i) stochastic order
in the (i) stochastic order 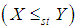 if
if 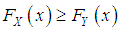 for all
for all 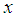 (ii) hazard rate order
(ii) hazard rate order 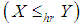 if
if 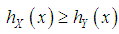 for all
for all 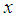 (iii) mean residual life order
(iii) mean residual life order 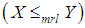 if
if 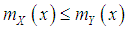 for all
for all 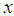 (iv) likelihood ratio order
(iv) likelihood ratio order 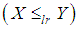 if
if 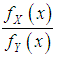 decreases in
decreases in 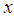 .The following stochastic ordering relationship given in Shaked and Shanthikumar (1994) are well known for stochastic ordering of distributions
.The following stochastic ordering relationship given in Shaked and Shanthikumar (1994) are well known for stochastic ordering of distributions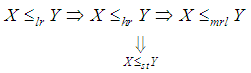 The Shanker distribution is ordered with respect to the strongest ‘likelihood ratio’ ordering which has been shown in the following theorem:Theorem: Let
The Shanker distribution is ordered with respect to the strongest ‘likelihood ratio’ ordering which has been shown in the following theorem:Theorem: Let 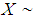 Shanker distributon
Shanker distributon 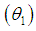 and
and 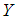
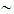 Shanker distribution
Shanker distribution 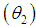 . If
. If 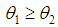 , then
, then 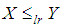 and hence
and hence 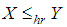 ,
,  and
and 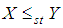 .Proof: We have
.Proof: We have 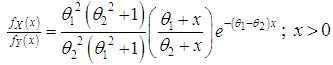 Now
Now 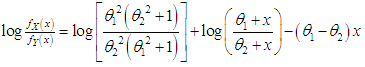 and
and 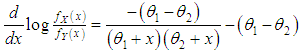 Thus for
Thus for 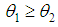 ,
, 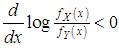 . This means that
. This means that 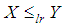 and hence
and hence 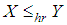 ,
, 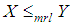 and
and 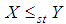 .
.6. Distribution of Order Statistics
- Let
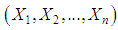 be a random sample of size
be a random sample of size 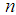 from Shanker distribution (1.3). Let
from Shanker distribution (1.3). Let 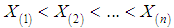 denote the corresponding order statistics. The p.d.f. and the c.d.f. of the th order statistic, say
denote the corresponding order statistics. The p.d.f. and the c.d.f. of the th order statistic, say 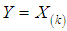 are given by
are given by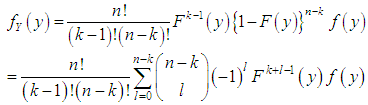 and
and 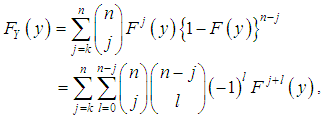 respectively, for
respectively, for 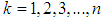 .Thus, the p.d.f. and the c.d.f of the th order statistics of Shanker distribution are obtained as
.Thus, the p.d.f. and the c.d.f of the th order statistics of Shanker distribution are obtained as 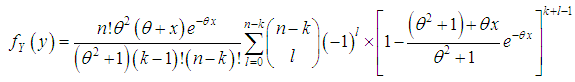 and
and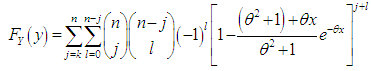
7. Renyi Entropy Measure
- The entropy of a random variable
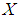 is the measure of variation of uncertainty. There are various entropy measures available in statistics literature but a popular entropy measure is Renyi entropy (1961). If
is the measure of variation of uncertainty. There are various entropy measures available in statistics literature but a popular entropy measure is Renyi entropy (1961). If 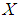 is a continuous random variable having probability density function
is a continuous random variable having probability density function 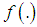 , then Renyi entropy is defined as
, then Renyi entropy is defined as 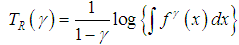 where
where 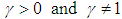 .Thus, the Renyi entropy for the Shanker distribution (1.3) can be obtained as
.Thus, the Renyi entropy for the Shanker distribution (1.3) can be obtained as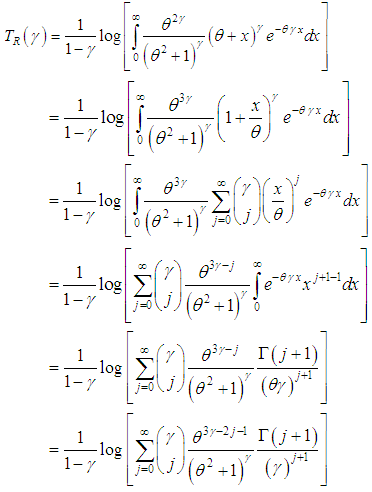
8. Mean Deviations from Mean and Median
- The amount of scatter in the population is measured to some extent by the totality of deviations usually from their mean and median and these are known as the mean deviation about the mean and the mean deviation about the median and are defined as
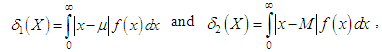 respectively, where
respectively, where 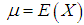 and
and 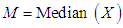 . The measures
. The measures 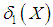 and
and 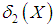 can be computed using the following simplified expressions
can be computed using the following simplified expressions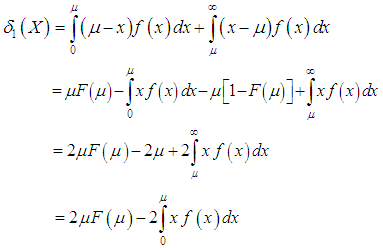 | (8.1) |
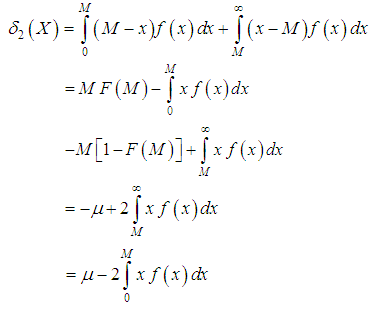 | (8.2) |
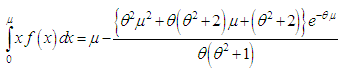 | (8.3) |
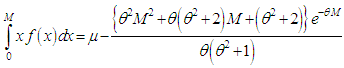 | (8.4) |
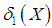 and
and 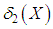 of Shanker distribution are obtained as
of Shanker distribution are obtained as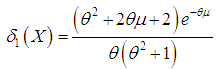 | (8.5) |
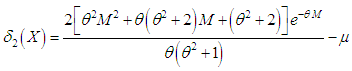 | (8.6) |
9. Bonferroni and Lorenz Curves and Indices
- The Bonferroni and Lorenz curves (Bonferroni, 1930) and Bonferroni and Gini indices have been used in economice to study income and poverty. Now a days, these curves and indices have many applications in other fields of knowledge including demography, reliability, insurance and medicine and engineering. The Bonferroni and Lorenz curves are defined as
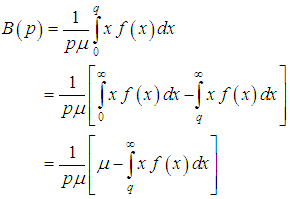 | (9.1) |
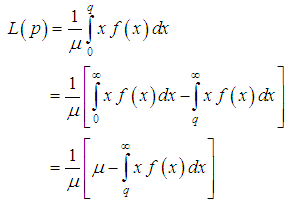 | (9.2) |
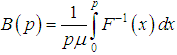 | (9.3) |
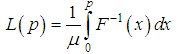 | (9.4) |
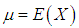 and
and 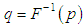 .The Bonferroni and Gini indices are thus defined as
.The Bonferroni and Gini indices are thus defined as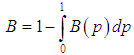 | (9.5) |
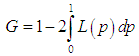 | (9.6) |
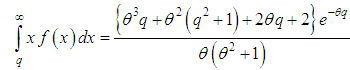 | (9.7) |
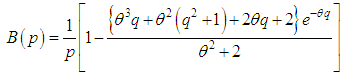 | (9.8) |
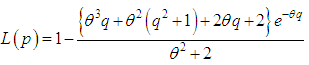 | (9.9) |
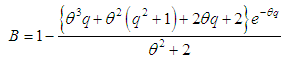 | (9.10) |
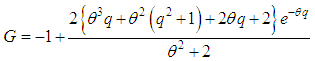 | (9.11) |
10. Stress-Strength Reliability
- The stress- strength reliability describes the life of a component which has random strength
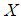 that is subjected to a random stress
that is subjected to a random stress 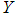 . When the stress applied to it exceeds the strength
. When the stress applied to it exceeds the strength 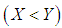 , the component fails instantly and the component will function satisfactorily till
, the component fails instantly and the component will function satisfactorily till 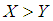 . Therefore,
. Therefore, 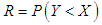 is a measure of component reliability and it is known as stress-strength parameter in statistics literature. It has wide applications in almost all areas of knowledge especially in engineering such as structures, deterioration of rocket motors, static fatigue of ceramic components, aging of concrete pressure vessels etc.Let
is a measure of component reliability and it is known as stress-strength parameter in statistics literature. It has wide applications in almost all areas of knowledge especially in engineering such as structures, deterioration of rocket motors, static fatigue of ceramic components, aging of concrete pressure vessels etc.Let 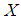 and
and 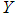 be independent strength and stress random variables having Shanker distribution (1.3) with parameter
be independent strength and stress random variables having Shanker distribution (1.3) with parameter 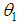 and
and 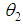 respectively. Then, the stress-strength reliability
respectively. Then, the stress-strength reliability 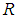 is obtained as
is obtained as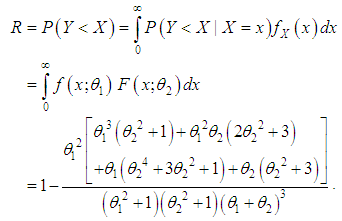
11. Estimation
11.1. Maximum Likelihood Estimate (MLE)
- Let
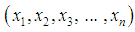 be a random sample of size
be a random sample of size 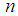 from Shanker distribution (1.3). The likelihood function,
from Shanker distribution (1.3). The likelihood function, 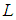 of (1.3) is given by
of (1.3) is given by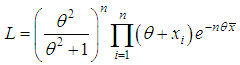 and so its log likelihood function is thus obtained as
and so its log likelihood function is thus obtained as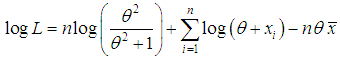 Now
Now 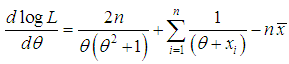 where
where 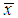 is the sample mean.The maximum likelihood estimate (MLE),
is the sample mean.The maximum likelihood estimate (MLE), 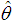 of
of 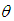 is the solution of the equation
is the solution of the equation 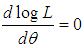 and so it can be obtained by solving the following non-linear equation
and so it can be obtained by solving the following non-linear equation 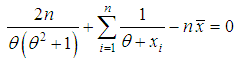 | (11.1.1) |
11.2. Method of Moment Estimate (MOME)
- Equating the population mean of the Shanker distribution to the corresponding sample mean, the method of moment estimate (MOME),
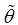 of
of 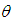 is the solution of the following cubic equation
is the solution of the following cubic equation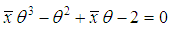 | (11.2.1) |
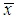 is the sample mean.
is the sample mean. 12. Applications
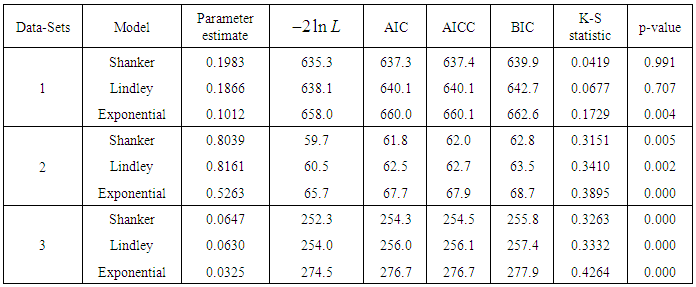
- The Shanker distribution has been fitted to a number of real lifetime data-sets and in almost all data-sets it gives better fit than exponential and Lindley distributions. In this section, we present the fittings of Shanker, Lindley and exponential distributions to three real lifetime data- sets to show the applicability and superiority of Shanker distribution over Lindley and exponential distributions.Data set 1: The first data - set represents the waiting times (in minutes) before service of 100 Bank customers and examined and analyzed by Ghitany et al (2008) for fitting the Lindley (1958) distribution. The data are as follows:0.8,0.8,1.3,1.5,1.8,1.9,1.9,2.1,2.6,2.7,2.9,3.1,3.2,3.3, 3.5,3.6,4.0,4.1,4.2,4.2,4.3,4.3,4.4,4.4,4.6,4.7,4.7,4.8,4.9,4.9,5.0,5.3,5.5,5.7,5.7,6.1,6.2,6.2,6.2,6.3,6.7,6.9,7.1,7.1,7.1,7.1,7.4,7.6,7.7,8.0,8.2,8.6,8.6,8.6,8.8,8.8,8.9,8.9,9.5,9.6,9.7,9.8,10.7, 10.9, 11.0, 11.0,11.1, 11.2, 11.2, 11.5, 11.9, 12.4, 12.5, 12.9, 13.0,13.1, 13.3, 13.6, 13.7, 13.9, 14.1, 15.4, 15.4, 17.3, 17.3, 18.1, 18.2, 18.4, 18.9, 19.0, 19.9, 20.6, 21.3,21.4, 21.9, 23.0, 27.0, 31.6, 33.1, 38.5.Data set 2: The second data - set represents the lifetime’s data relating to relief times (in minutes) of 20 patients receiving an analgesic and reported by Gross and Clark (1975, P. 105). The data are as follows:1.1, 1.4, 1.3, 1.7, 1.9, 1.8, 1.6, 2.2, 1.7, 2.7, 4.1, 1.8, 1.5, 1.2, 1.4, 3.0, 1.7, 2.3, 1.6, 2.0Data set 3: The third data set is the strength data of glass of the aircraft window reported by Fuller et al (1994)18.83, 20.80, 21.657, 23.03, 23.23, 24.05, 24.321, 25.50, 25.52, 25.80, 26.69, 26.77, 26.78, 27.05, 27.67, 29.90, 31.11, 33.20, 33.73, 33.76, 33.89, 34.76, 35.75, 35.91, 36.98, 37.08, 37.09, 39.58, 44.045, 45.29, 45.381 In order to compare exponential, Lindley and Shanker distributions,
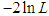 , AIC (Akaike Information Criterion), AICC (Akaike Information Criterion Corrected), BIC (Bayesian Information Criterion), K-S Statistics (Kolmogorov-Smirnov Statistics) for three real lifetime data sets have been computed and presented in table 1. The formulae for computing AIC, AICC, BIC, and K-S Statistics are as follows:
, AIC (Akaike Information Criterion), AICC (Akaike Information Criterion Corrected), BIC (Bayesian Information Criterion), K-S Statistics (Kolmogorov-Smirnov Statistics) for three real lifetime data sets have been computed and presented in table 1. The formulae for computing AIC, AICC, BIC, and K-S Statistics are as follows: 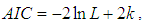 ,
, 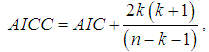 ,
, 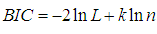 and
and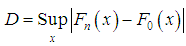 , where
, where 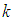 = the number of parameters,
= the number of parameters, 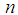 = the sample size and
= the sample size and 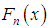 is the empirical distribution function. The best distribution which gives much closer fit to lifetime data-sets corresponds to lower
is the empirical distribution function. The best distribution which gives much closer fit to lifetime data-sets corresponds to lower 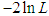 , AIC, AICC, BIC, and K-S statistics
, AIC, AICC, BIC, and K-S statistics
|
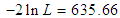 ) introduced by Abouammoh et al (2015) and a two parameter Lindley distribution (with
) introduced by Abouammoh et al (2015) and a two parameter Lindley distribution (with 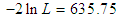 ) introduced by Shanker and Mishra (2013 a).
) introduced by Shanker and Mishra (2013 a).13. Concluding Remarks
- In the present paper a one parameter lifetime distribution named, “Shanker distribution” has been introduced. Its various mathematical properties including shape, moments and associated measures, hazard rate and mean residual life functions, stochastic ordering, mean deviations, and order statistics have been discussed. Further, expressions for Bonferroni and Lorenz curves, Renyi entropy measure and stress-strength reliability of the proposed distribution have been derived. The conditions of over-dispersion, equi-dispersion, and under-dispersion of Shanker distribution have been discussed along with the Lindley and exponential distributions. The method of moments and the method of maximum likelihood estimation have also been discussed for estimating its parameter. Finally, the goodness of fit test using K-S Statistics (Kolmogorov-Smirnov Statistics) for three real lifetime data- sets have been presented to demonstrate its applicability and superiority over exponential and Lindley distributions.
ACKNOWLEDGEMENTS
- The author is grateful to the anonymous reviewer for some helpful comments.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML