-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Statistics and Applications
p-ISSN: 2168-5193 e-ISSN: 2168-5215
2015; 5(3): 120-123
doi:10.5923/j.statistics.20150503.04
A New Method of Construction of E-optimal Generalized Group Divisible Designs with Two Groups
D. K. Ghosh1, Sreejith V.2, Alex Thannippara3, S. C. Bagui4
1Department of Mathematics and Statistics, Saurastra University, Rajkot, Gujarat, India
2Department of Statistics, Govt. College for Women, University of Kerala, Thiruvananthapuram, India
3Department of Statistics, St. Thomas College, Mahatma Gandhi University, Kottayam, Kerala, India
4Department of Mathematics and Statistics, The University of West Florida, Pensacola, USA
Correspondence to: S. C. Bagui, Department of Mathematics and Statistics, The University of West Florida, Pensacola, USA.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
In this paper, we consider the construction of generalized group divisible designs with two groups (GGDD(2)) from balanced incomplete block designs (BIBD). We also verify the E-optimality of these designs.
Keywords: Generalized Group Divisible Design (GGDD), Balanced Incomplete Block Design (BIBD), E-optimality
Cite this paper: D. K. Ghosh, Sreejith V., Alex Thannippara, S. C. Bagui, A New Method of Construction of E-optimal Generalized Group Divisible Designs with Two Groups, International Journal of Statistics and Applications, Vol. 5 No. 3, 2015, pp. 120-123. doi: 10.5923/j.statistics.20150503.04.
Article Outline
1. Introduction
- Generalized Group Divisible Designs and their optimality have been studied by Jacroux (1980) [1], Srivastav and Morgan (1998) [2], Thannippara et al. (2009) [3], Ghosh et al. (2012) [4] and others. In this article we present a new method for constructing generalized group divisible designs with two groups from balanced incomplete block designs. We prove that the constructed generalized group divisible designs are also E-optimal. Balanced Incomplete Block Designs (BIBD): An incomplete block design with
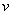 treatments allocated over
treatments allocated over  blocks, each of size
blocks, each of size 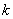 (
(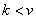 ), such that each treatment appears in
), such that each treatment appears in 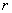 blocks, no treatment appears more than once in a block and each pair of treatments appears in exactly
blocks, no treatment appears more than once in a block and each pair of treatments appears in exactly 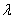 blocks, is called a balanced incomplete block design (BIBD). The numbers
blocks, is called a balanced incomplete block design (BIBD). The numbers 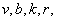 and
and 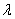 are called the parameters of the design. Generalized Group Divisible Designs with two groups (GGDD(2)): Let
are called the parameters of the design. Generalized Group Divisible Designs with two groups (GGDD(2)): Let 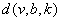 be any design having
be any design having 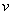 treatments allocated in
treatments allocated in 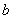 blocks each of size
blocks each of size 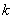 . Then the design
. Then the design 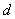 is a generalized group divisible design with two groups if the treatments can be divided into two mutually disjoint sets
is a generalized group divisible design with two groups if the treatments can be divided into two mutually disjoint sets 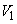 and
and 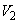 , each with size
, each with size 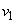 and
and 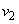 respectively
respectively 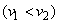 , such that(i) for
, such that(i) for 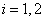 and for all
and for all 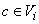 ,
, 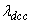
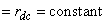 (ii) for all
(ii) for all 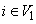 and
and 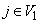
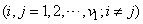 ,
, 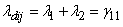 (say),(iii) for all
(say),(iii) for all 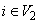 and
and 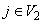 ,
, 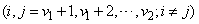 ,
, 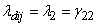 (say), and (iv) for all
(say), and (iv) for all 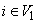 and
and 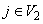
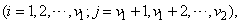 ,
, 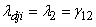 (say)where
(say)where 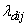 denotes the
denotes the 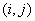 th entry of the concurrence matrix
th entry of the concurrence matrix 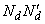 . E-Optimality: Let
. E-Optimality: Let 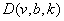 be a set of designs each having
be a set of designs each having 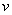 treatments allocated in
treatments allocated in 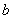 blocks of size
blocks of size 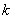 each. A design
each. A design 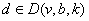 is said to be E-Optimal if it maximizes
is said to be E-Optimal if it maximizes 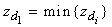 where
where 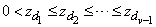 are the non-zero eigenvalues of the C-matrix of the design.
are the non-zero eigenvalues of the C-matrix of the design. 2. Method of Construction
- Theorem 2.1. The design obtained by merging two BIBDs with same block sizes is a generalized group divisible design with two groups. Proof. Let
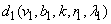 and
and 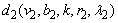 be two balanced incomplete block designs with treatments labelled
be two balanced incomplete block designs with treatments labelled 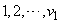 and
and 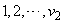
 , respectively. Suppose that we merge these two designs to obtain a design, say,
, respectively. Suppose that we merge these two designs to obtain a design, say, 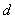 . Obviously, the new design has
. Obviously, the new design has 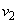 treatments and
treatments and 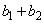 blocks. The
blocks. The  treatments in the design can be grouped into two, viz.,
treatments in the design can be grouped into two, viz., 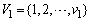 and
and 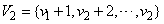 such that the treatments in
such that the treatments in 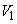 i.e.,
i.e., 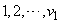 will be replicated
will be replicated  times and those in
times and those in 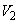 , i.e.,
, i.e., 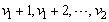 will be replicated
will be replicated 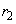 times. In addition,for all
times. In addition,for all 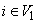 and
and 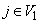 ,
, 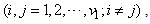
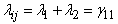 (say),for all
(say),for all 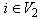 and
and 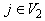 ,
, 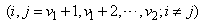 ,
, 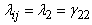 (say), and for all
(say), and for all 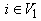 and
and 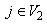 ,
, 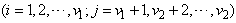 ,
, 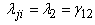 (say).Thus, the design
(say).Thus, the design 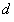 is a GGDD(2).
is a GGDD(2).3. Example
- Consider the design
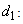
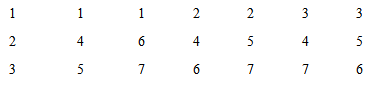 and the design
and the design 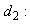
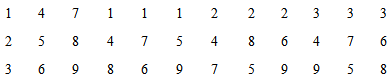 Note that
Note that 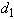 is a BIBD(7, 7, 3, 3, 1) and
is a BIBD(7, 7, 3, 3, 1) and 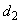 is a BIBD (9, 12, 3, 4, 1). Combing these two balanced incomplete block designs, we get a new design
is a BIBD (9, 12, 3, 4, 1). Combing these two balanced incomplete block designs, we get a new design 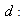
 Obviously, the design
Obviously, the design 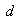 is a GGDD(2) with
is a GGDD(2) with 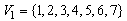 and
and 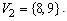 The parameters of
The parameters of 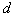 are
are 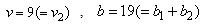 ,
, 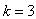 ,
, 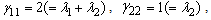 and
and 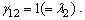 The number of replications for the treatments in
The number of replications for the treatments in 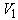 is
is 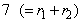 and that for the treatments in
and that for the treatments in 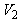 is
is 
4. E-Optimality
- Theorem 4.1. The class of GGDD’s constructed in section 2 is E-optimal. Proof. We will prove the theorem using the Lemma 4.1 given below. It can be verified that for the class of GGDD’s constructed as per Theorem 2.1, the smallest off-diagonal entry is
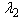 and the smallest value of replication is
and the smallest value of replication is 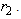 Keeping this in mind, we shall proceed as follows: Let
Keeping this in mind, we shall proceed as follows: Let 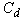 denote the
denote the 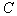 -matrix of the design
-matrix of the design 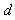 . Consider the matrix
. Consider the matrix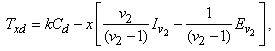 where
where 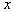 is a real number,
is a real number, 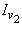 is the
is the 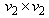 identity matrix, and
identity matrix, and 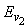 is the
is the 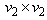 matrix of ones. The matrix
matrix of ones. The matrix 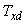 has the following form
has the following form 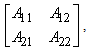 where
where 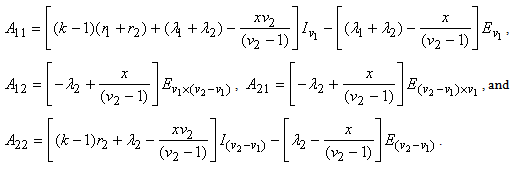 ,The eigenvalues of
,The eigenvalues of  are
are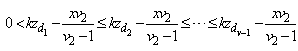 | (1) |
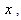 let
let 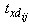 denote the
denote the 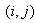 th entry of
th entry of 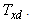 Note that for all
Note that for all 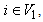
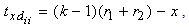 | (2) |
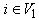 and
and 
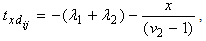 | (3) |
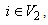
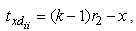 | (4) |
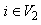 and
and 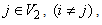
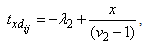 | (5) |
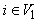 and
and 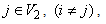
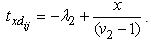 | (6) |
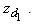 Letting
Letting 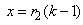 in (4), we get, for all
in (4), we get, for all  Similarly, for all
Similarly, for all 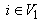 and
and 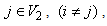 from (6) we get
from (6) we get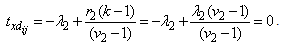 and for all
and for all 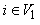 and
and 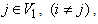 from (3),
from (3),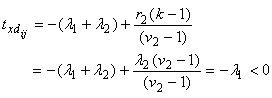 .Hence
.Hence 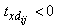 for all
for all 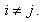 Thus
Thus 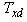 must possess a negative eigenvalue or at least two zero eigenvalues. Now from (1), we get
must possess a negative eigenvalue or at least two zero eigenvalues. Now from (1), we get 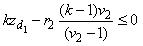 i.e.,
i.e., 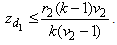 Next we obtain a lower bound on
Next we obtain a lower bound on 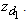 Note that
Note that 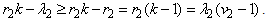
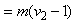 Consider the matrix
Consider the matrix 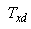 with
with  . From (1), we have
. From (1), we have 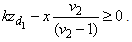 Now substituting
Now substituting 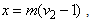 and rearranging terms we have
and rearranging terms we have 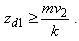 Combining the upper and lower bound obtained above, we have
Combining the upper and lower bound obtained above, we have 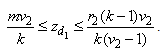 Further if
Further if 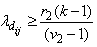 for all
for all 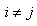 , then
, then 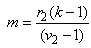 so that
so that  This gives
This gives  Hence, by the Lemma 4.1 given below, the class of GGDD’s constructed using Theorem 2.1 is E-optimal.We state the Lemma 4.1 which is given in Jacroux (1980) [1] and used in the proof of the above theorem.Lemma 4.1. Suppose
Hence, by the Lemma 4.1 given below, the class of GGDD’s constructed using Theorem 2.1 is E-optimal.We state the Lemma 4.1 which is given in Jacroux (1980) [1] and used in the proof of the above theorem.Lemma 4.1. Suppose 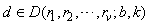 has
has  -matrix
-matrix 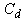 and
and 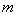 is the smallest off-diagonal element occurring in the matrix
is the smallest off-diagonal element occurring in the matrix 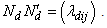 Then
Then 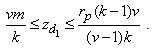 Further, if
Further, if 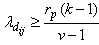 for all
for all 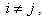 then
then 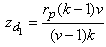 and hence
and hence 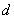 is E-optimal in
is E-optimal in 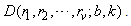
5. Illustrations
- Consider the example of GGDD(2) constructed in Section 3. The incidence matrix
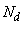 of this design is given by
of this design is given by  The concurrence matrix
The concurrence matrix 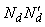 of this design is given by
of this design is given by The information matrix
The information matrix 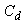 is given by
is given by 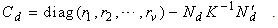 Since
Since 
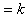 , therefore
, therefore 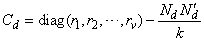 . In this example
. In this example 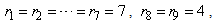 and
and 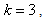 finally we get the information matrix
finally we get the information matrix 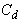 as
as 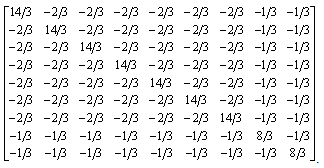 Here
Here 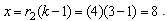 On substituting the values of
On substituting the values of 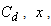 and other parameters, we obtain the matrix
and other parameters, we obtain the matrix 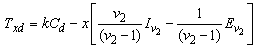 as
as  The nonzero eigenvalues of
The nonzero eigenvalues of  are 5.33 and 3. The minimum nonzero eigenvalue of
are 5.33 and 3. The minimum nonzero eigenvalue of  is and satisfies the conditions of Lemma 4.1. Hence the design
is and satisfies the conditions of Lemma 4.1. Hence the design 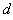 constructed in Section 3 is E-optimal.
constructed in Section 3 is E-optimal.ACKNOWLEDGEMENTS
- The authors would like to thank the referee for his/her constructive suggestions on the earlier version of the paper.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML