Firas H. Thanoon
Department of Mathematics, Faculty of Science & Education-Akre, University of Duhok, Iraq
Correspondence to: Firas H. Thanoon, Department of Mathematics, Faculty of Science & Education-Akre, University of Duhok, Iraq.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The research deals with the choice of approach or the appropriate method of estimation, As a topic to be important, especially if you do not check some assumptions of linear form, such as the hypothesis of normal distribution for random errors, and the state of data pollution with abnormal values, since such cases have a negative impact on the estimation of Linear regression model parameters and thus the consequences would be misleading. Hence came the importance of using techniques or robust methods in matters of estimating parameters of linear regression model methods. Robust methods are known as resistant of abnormal values and other violations of model assumptions and appropriate for a broad category of distributions. A comparison in the study has been made between least absolute deviations method (Approach Iteratively Reweighted Least Squares) and least squares method, it has been made by using the empirical part which was the generation of experimental data depending on comparison criteria (standard mean square error of the model , standard mean square error for the parameters estimated and standard average deviation of absolute error), it was discovered that the least absolute deviations method is more efficient in estimating the parameters in all cases the distribution of errors for the model and especially in the case of following normal distribution and in the case of contamination of the data with abnormal values.
Keywords:
L1-norm, L2-norm, Least absolute deviations, Ordinary least square, Outliers, Iterative weighted least squares
Cite this paper: Firas H. Thanoon, Robust Regression by Least Absolute Deviations Method, International Journal of Statistics and Applications, Vol. 5 No. 3, 2015, pp. 109-112. doi: 10.5923/j.statistics.20150503.02.
1. Introduction
Least squares regression is sensitive to outlier points. It has dominated the statistical literature for a long time. This dominance and popularity of the least squares regression can be ascribed, at least partially to the fact that the theory is simple, well developed and documented. The computer packages are also easily available. The least squares regression is optimal and in the maximum likelihood estimators of the unknown parameters of the model if the errors are independent and follow a normal distribution with mean zero and a common (though unknown) variance 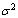 .The least squares regression is very far from the optimal in many non-Gaussian situations, especially when the errors follow distributions with longer tails. For the regression problems Huber (1973) [7] stated “just a single grossly outlying observation may spoil the least squares estimate, and, moreover, outliers are much harder to spot in the regression than in the simple location case”. The outliers occurring with extreme values of the regressor variables can be especially disruptive. Andrews (1974) [3] noted that even when the errors follow a normal distribution, alternatives to least squares may be required; especially if the form of the model is not exactly known. Further, least squares are not very satisfactory if the quadraticloss function is not a satisfactory measure of the loss. Loss denotes the seriousness of the nonzero prediction error to the investigator, where prediction error is the difference between the predicted and the observed value of the response variable. Meyer & Glauber (1964) [9] stated that for at least certain economic problems absolute error may be amore satisfactory measure of loss than the squared error. The least absolute deviation errors regression (or for brevity, absolute errors regression) overcomes the aforementioned drawbacks of the least squares regression and provides an attractive alternative. It is less sensitive than least squares regression to the extreme errors and assumes absolute error loss function. Because of its resistance to outliers, it provides a better starting point than the least squares regression for certain robust regression procedures. Unlike, other robust regression procedures, it does not require (a rejection parameter). It may be noted that the absolute errors estimates are maximum likelihood and hence asymptotically efficient when the errors follow the Laplace distribution.Many quantitative models are utilized to diagnose and evaluate the response to studies of their regression analysis is an important statistical tool that is routinely applied in most applied sciences. To ease the model formulation and computation, some desired assumptions such as normality of the response variable are made on the regression structure. Out of many possible regression techniques for fitting the model, the ordinary least squares (OLS) method has been traditionally adopted due to the ease of computation. However, there is presently a widespread awareness of the dangers posed by the occurrence of outliers in the OLS estimates (Rousseuw and Leroy, 2003) [11]. The robustness method is considered as an alternative to a least squares method, especially if the regression model does not meet the fundamental assumptions or there are violations of it in the least square method. The estimation of significance becomes impaired; furthermore the prediction and estimation of the model may become biased.
.The least squares regression is very far from the optimal in many non-Gaussian situations, especially when the errors follow distributions with longer tails. For the regression problems Huber (1973) [7] stated “just a single grossly outlying observation may spoil the least squares estimate, and, moreover, outliers are much harder to spot in the regression than in the simple location case”. The outliers occurring with extreme values of the regressor variables can be especially disruptive. Andrews (1974) [3] noted that even when the errors follow a normal distribution, alternatives to least squares may be required; especially if the form of the model is not exactly known. Further, least squares are not very satisfactory if the quadraticloss function is not a satisfactory measure of the loss. Loss denotes the seriousness of the nonzero prediction error to the investigator, where prediction error is the difference between the predicted and the observed value of the response variable. Meyer & Glauber (1964) [9] stated that for at least certain economic problems absolute error may be amore satisfactory measure of loss than the squared error. The least absolute deviation errors regression (or for brevity, absolute errors regression) overcomes the aforementioned drawbacks of the least squares regression and provides an attractive alternative. It is less sensitive than least squares regression to the extreme errors and assumes absolute error loss function. Because of its resistance to outliers, it provides a better starting point than the least squares regression for certain robust regression procedures. Unlike, other robust regression procedures, it does not require (a rejection parameter). It may be noted that the absolute errors estimates are maximum likelihood and hence asymptotically efficient when the errors follow the Laplace distribution.Many quantitative models are utilized to diagnose and evaluate the response to studies of their regression analysis is an important statistical tool that is routinely applied in most applied sciences. To ease the model formulation and computation, some desired assumptions such as normality of the response variable are made on the regression structure. Out of many possible regression techniques for fitting the model, the ordinary least squares (OLS) method has been traditionally adopted due to the ease of computation. However, there is presently a widespread awareness of the dangers posed by the occurrence of outliers in the OLS estimates (Rousseuw and Leroy, 2003) [11]. The robustness method is considered as an alternative to a least squares method, especially if the regression model does not meet the fundamental assumptions or there are violations of it in the least square method. The estimation of significance becomes impaired; furthermore the prediction and estimation of the model may become biased.
2. Least Square or L2-norm Method (OLS)
Utilizing the Ordinary Least Squares (OLS) method, the estimator 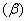 is found byminimizing the sum of squared residuals:
is found byminimizing the sum of squared residuals: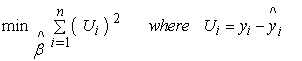 This gives the OLS estimator for
This gives the OLS estimator for 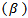 as:
as: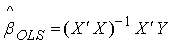 | (1) |
The OLS estimate is optimal when the error distribution is assumed to be normal (Hampel 1974 [6] and Mosteller & Tukey, 1977 [10]) in the presence of influential observations, robust regression is a suitable alternative to the OLS , Robust procedures have been the focus of many studies recently, all of which triggered by the ideas of Hampel 1974 [6] .
2.1. Mean Square Error for Model
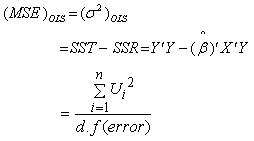 | (2) |
2.2. Mean Square Error for Estimator
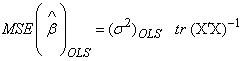 | (3) |
2.3. Mean Absolute Error
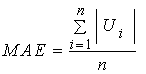 | (4) |
3. Least Absolute Deviation (or L1-norm) Method (LAD)
This estimator obtains a higher efficiency than OLS through minimizing the sum of the absolute errors: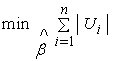 Once LAD estimation is justified and its edge over the OLS estimation (in an appropriate condition) is established, an efficient algorithm to obtain LAD estimates has a practical significance. A progress in this direction was made by Abdelmalek (1971, 1974) [1, 2], Fair (1974) [5], Schlossmacher (1973) [13] and Spyropoulos, Kiountouzis & Young (1973) [14], They also proposed an improved algorithm for L1 estimation that is very similar to iterative weighted least squares.Even though calculus cannot be used to obtain an explicit formula for the solution to the L1-regression problem, Robert (2001) [12], it can be used to obtain an iterative procedure when properly initialized, converges to the solution of the L1-regression problem. The resulting iterative process is called iteratively Reweighted least squares. In this section, we briefly discuss this method. We start by considering the objective function for L1-regression, Robert (2001) [12]:
Once LAD estimation is justified and its edge over the OLS estimation (in an appropriate condition) is established, an efficient algorithm to obtain LAD estimates has a practical significance. A progress in this direction was made by Abdelmalek (1971, 1974) [1, 2], Fair (1974) [5], Schlossmacher (1973) [13] and Spyropoulos, Kiountouzis & Young (1973) [14], They also proposed an improved algorithm for L1 estimation that is very similar to iterative weighted least squares.Even though calculus cannot be used to obtain an explicit formula for the solution to the L1-regression problem, Robert (2001) [12], it can be used to obtain an iterative procedure when properly initialized, converges to the solution of the L1-regression problem. The resulting iterative process is called iteratively Reweighted least squares. In this section, we briefly discuss this method. We start by considering the objective function for L1-regression, Robert (2001) [12]: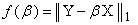 | (5) |
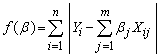 | (6) |
Differentiating this objective function is a problem, since it involves absolute values However, the absolute value function: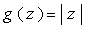 is differentiable everywhere except at one point: z = 0. Furthermore, we can use the following simple formula for the derivative, where it exists
is differentiable everywhere except at one point: z = 0. Furthermore, we can use the following simple formula for the derivative, where it exists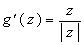 Using this formula to differentiate f with respect to each variable, and setting the derivatives to zero, we get the following equations for critical points
Using this formula to differentiate f with respect to each variable, and setting the derivatives to zero, we get the following equations for critical points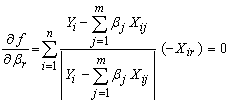 | (7) |
Where r =1, 2, …., m Can rewrite (7) as: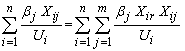 | (8) |
Let 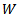 denote the diagonal matrix, DasGupta & Mishra (2004) [4], where:
denote the diagonal matrix, DasGupta & Mishra (2004) [4], where: We can write these equations in matrix notation as follows:
We can write these equations in matrix notation as follows: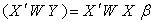 This equation can’t be solved for x as we were able to do in L2-regression because of the dependence of the diagonal matrix on
This equation can’t be solved for x as we were able to do in L2-regression because of the dependence of the diagonal matrix on 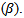 But let us rearrange this system ofequations by multiplying both sides by of:
But let us rearrange this system ofequations by multiplying both sides by of: 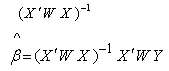 | (9) |
This formula suggests an iterative scheme that hopefully converges to a solution. Indeed, we start by initializing 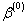 arbitrarily and then use the above formula to successively compute new approximations. If we let
arbitrarily and then use the above formula to successively compute new approximations. If we let 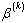 denote the approximation at the kth iteration, then the update formula can be expressed as:
denote the approximation at the kth iteration, then the update formula can be expressed as: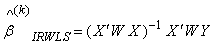 | (10) |
Assuming only that the matrix inverse exists at every iteration, one can show that this iteration scheme converges to a solution to the L1-regression problem. LAD regression estimates are obtainable from the function L1 fit in the computer language(S-PLUS) and from the robust regression package ROBSYS, Levent, Soner, Gokhan & Hulya (2006) [8].
3.1. Mean Square Error for Model
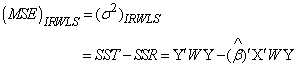 | (11) |
3.2. Mean Square Error for Estimator
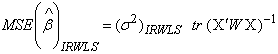 | (12) |
3.3. Mean Absolute Error
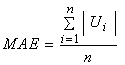 | (13) |
4. The Simulation Study
The following model was used 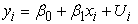 | (14) |
Now, 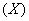 was obtained from a set numbers (1, 1.1, 1.2, 1.3 ...),
was obtained from a set numbers (1, 1.1, 1.2, 1.3 ...), 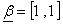 where, distribution of errors (normal, Contaminant, Laplace, Cauchy). And size of random: n=20, n=50, n=100 and n=200.
where, distribution of errors (normal, Contaminant, Laplace, Cauchy). And size of random: n=20, n=50, n=100 and n=200.
5. Concluding Remarks
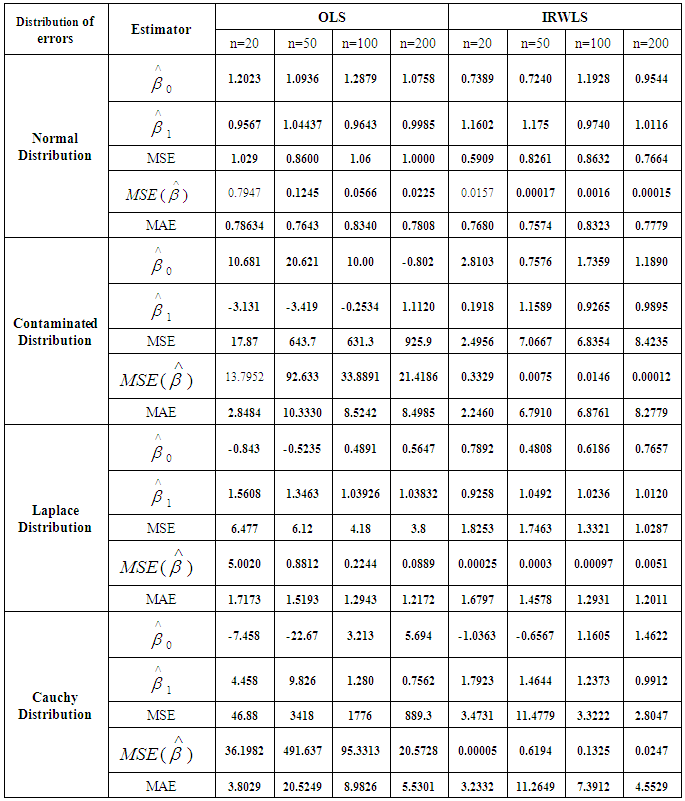
Table (1). OLS& IRWLS estimators
 |
| |
|
Through the above table:1. It has been shown that the LAD (L1-norm) is more efficient in using IRWLS approach to estimate the parameters in all cases of distributions of error for the model, especially in the case of following normal distribution in the LS method in all sample sizes, and this was confirmed by all standards of comparison used in the research.2. The method of LAD style is very suitable and efficient for estimating the parameters and regression analysis, for using the absolute deviations of error in the estimate.
References
| [1] | Abdelmalek, NN (1971). “Linear L1 Approximation for a Discrete Point Set and L1-Solutions of Overdetermined Linear Equations”, Journal of Assoc. Comput. Mach., 18. (47-41). |
| [2] | Abdelmalek, NN (1974). “On the Discrete Linear L1 Approximation and L1 Solution ofOver- determined Linear Equations”, Journal of Approximation Theory,11(35-53). |
| [3] | Andrews, D.F. (1974). A robust method formultiple linear regression. Technometrics 16, 523-531. |
| [4] | DasGupta, M & Mishra, SK, (2004), "Least Absolute Deviation Estimation of Linear Econometric Models: A Literature Review", http://mpra.ub.uni-muenchen.de/1781. |
| [5] | Fair, RC (1974). “On the Robust Estimation of Econometric Models”, Annals ofEconomic and Social Measurement, 3 (667-677). |
| [6] | Hampel F R, (1974)," The influence curve and its role in robust estimation", Journal of theAmerican Statistical Association, 69, 383-393. |
| [7] | Huber, PJ (1973). "Robust Regression: Asymptotics, Conjectures, and Monte Carlo" The Annals of Statistics, 1 (799-821). |
| [8] | Levent, S; Soner, C; Gokhan, G & Hulya, A, (2006), "A Comparative Study of Least Square Method and Least Absolute Deviation Method for Parameters Estimation in Length-Weight Relationship for White Grouper (Ephinephelus Aeneus)", Pakistan Journal of Biological Sciences 9(15): 2919-2921. |
| [9] | Meyer, JR & Glauber R.R (1964). "Investment Decisions: Economic Forecastingand Public Policy", Harvard Business School Press, Cambridge, Massachusetts. |
| [10] | Mosteller and Tukey J W , (1977)," Data Analysis and Regression. Reading", MA: Addison Wesley. |
| [11] | Rousseuw P. J., & Leroy A. M., (2003)," Robust Regression and Outlier Detection", New York, John Willy. |
| [12] | Robert J. Vanderbei,(2001),"Linear Programming: Foundations and Extensions", Robert J. Vanderbei,USA |
| [13] | Schlossmacher, EJ (1973). “An Iterative Technique for Absolute Deviations Curve Fitting”, Journal of the American Statistical Association, 68 (857-859). |
| [14] | Spyropoulous, K; Kiountouzis, E & Young, A (1973). “Discrete Approximation in theL1 Norm”, Computer Journal, 16 (180-186). |

 .The least squares regression is very far from the optimal in many non-Gaussian situations, especially when the errors follow distributions with longer tails. For the regression problems Huber (1973) [7] stated “just a single grossly outlying observation may spoil the least squares estimate, and, moreover, outliers are much harder to spot in the regression than in the simple location case”. The outliers occurring with extreme values of the regressor variables can be especially disruptive. Andrews (1974) [3] noted that even when the errors follow a normal distribution, alternatives to least squares may be required; especially if the form of the model is not exactly known. Further, least squares are not very satisfactory if the quadraticloss function is not a satisfactory measure of the loss. Loss denotes the seriousness of the nonzero prediction error to the investigator, where prediction error is the difference between the predicted and the observed value of the response variable. Meyer & Glauber (1964) [9] stated that for at least certain economic problems absolute error may be amore satisfactory measure of loss than the squared error. The least absolute deviation errors regression (or for brevity, absolute errors regression) overcomes the aforementioned drawbacks of the least squares regression and provides an attractive alternative. It is less sensitive than least squares regression to the extreme errors and assumes absolute error loss function. Because of its resistance to outliers, it provides a better starting point than the least squares regression for certain robust regression procedures. Unlike, other robust regression procedures, it does not require (a rejection parameter). It may be noted that the absolute errors estimates are maximum likelihood and hence asymptotically efficient when the errors follow the Laplace distribution.Many quantitative models are utilized to diagnose and evaluate the response to studies of their regression analysis is an important statistical tool that is routinely applied in most applied sciences. To ease the model formulation and computation, some desired assumptions such as normality of the response variable are made on the regression structure. Out of many possible regression techniques for fitting the model, the ordinary least squares (OLS) method has been traditionally adopted due to the ease of computation. However, there is presently a widespread awareness of the dangers posed by the occurrence of outliers in the OLS estimates (Rousseuw and Leroy, 2003) [11]. The robustness method is considered as an alternative to a least squares method, especially if the regression model does not meet the fundamental assumptions or there are violations of it in the least square method. The estimation of significance becomes impaired; furthermore the prediction and estimation of the model may become biased.
.The least squares regression is very far from the optimal in many non-Gaussian situations, especially when the errors follow distributions with longer tails. For the regression problems Huber (1973) [7] stated “just a single grossly outlying observation may spoil the least squares estimate, and, moreover, outliers are much harder to spot in the regression than in the simple location case”. The outliers occurring with extreme values of the regressor variables can be especially disruptive. Andrews (1974) [3] noted that even when the errors follow a normal distribution, alternatives to least squares may be required; especially if the form of the model is not exactly known. Further, least squares are not very satisfactory if the quadraticloss function is not a satisfactory measure of the loss. Loss denotes the seriousness of the nonzero prediction error to the investigator, where prediction error is the difference between the predicted and the observed value of the response variable. Meyer & Glauber (1964) [9] stated that for at least certain economic problems absolute error may be amore satisfactory measure of loss than the squared error. The least absolute deviation errors regression (or for brevity, absolute errors regression) overcomes the aforementioned drawbacks of the least squares regression and provides an attractive alternative. It is less sensitive than least squares regression to the extreme errors and assumes absolute error loss function. Because of its resistance to outliers, it provides a better starting point than the least squares regression for certain robust regression procedures. Unlike, other robust regression procedures, it does not require (a rejection parameter). It may be noted that the absolute errors estimates are maximum likelihood and hence asymptotically efficient when the errors follow the Laplace distribution.Many quantitative models are utilized to diagnose and evaluate the response to studies of their regression analysis is an important statistical tool that is routinely applied in most applied sciences. To ease the model formulation and computation, some desired assumptions such as normality of the response variable are made on the regression structure. Out of many possible regression techniques for fitting the model, the ordinary least squares (OLS) method has been traditionally adopted due to the ease of computation. However, there is presently a widespread awareness of the dangers posed by the occurrence of outliers in the OLS estimates (Rousseuw and Leroy, 2003) [11]. The robustness method is considered as an alternative to a least squares method, especially if the regression model does not meet the fundamental assumptions or there are violations of it in the least square method. The estimation of significance becomes impaired; furthermore the prediction and estimation of the model may become biased.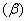 is found byminimizing the sum of squared residuals:
is found byminimizing the sum of squared residuals: This gives the OLS estimator for
This gives the OLS estimator for 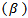 as:
as: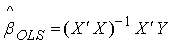
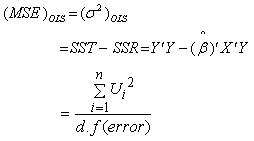
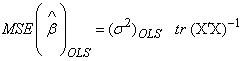
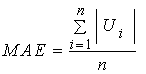
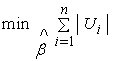 Once LAD estimation is justified and its edge over the OLS estimation (in an appropriate condition) is established, an efficient algorithm to obtain LAD estimates has a practical significance. A progress in this direction was made by Abdelmalek (1971, 1974) [1, 2], Fair (1974) [5], Schlossmacher (1973) [13] and Spyropoulos, Kiountouzis & Young (1973) [14], They also proposed an improved algorithm for L1 estimation that is very similar to iterative weighted least squares.Even though calculus cannot be used to obtain an explicit formula for the solution to the L1-regression problem, Robert (2001) [12], it can be used to obtain an iterative procedure when properly initialized, converges to the solution of the L1-regression problem. The resulting iterative process is called iteratively Reweighted least squares. In this section, we briefly discuss this method. We start by considering the objective function for L1-regression, Robert (2001) [12]:
Once LAD estimation is justified and its edge over the OLS estimation (in an appropriate condition) is established, an efficient algorithm to obtain LAD estimates has a practical significance. A progress in this direction was made by Abdelmalek (1971, 1974) [1, 2], Fair (1974) [5], Schlossmacher (1973) [13] and Spyropoulos, Kiountouzis & Young (1973) [14], They also proposed an improved algorithm for L1 estimation that is very similar to iterative weighted least squares.Even though calculus cannot be used to obtain an explicit formula for the solution to the L1-regression problem, Robert (2001) [12], it can be used to obtain an iterative procedure when properly initialized, converges to the solution of the L1-regression problem. The resulting iterative process is called iteratively Reweighted least squares. In this section, we briefly discuss this method. We start by considering the objective function for L1-regression, Robert (2001) [12]: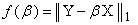
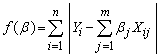
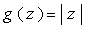 is differentiable everywhere except at one point: z = 0. Furthermore, we can use the following simple formula for the derivative, where it exists
is differentiable everywhere except at one point: z = 0. Furthermore, we can use the following simple formula for the derivative, where it exists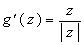 Using this formula to differentiate f with respect to each variable, and setting the derivatives to zero, we get the following equations for critical points
Using this formula to differentiate f with respect to each variable, and setting the derivatives to zero, we get the following equations for critical points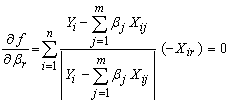
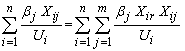
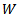 denote the diagonal matrix, DasGupta & Mishra (2004) [4], where:
denote the diagonal matrix, DasGupta & Mishra (2004) [4], where: We can write these equations in matrix notation as follows:
We can write these equations in matrix notation as follows: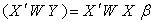 This equation can’t be solved for x as we were able to do in L2-regression because of the dependence of the diagonal matrix on
This equation can’t be solved for x as we were able to do in L2-regression because of the dependence of the diagonal matrix on 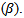 But let us rearrange this system ofequations by multiplying both sides by of:
But let us rearrange this system ofequations by multiplying both sides by of: 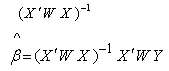
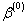 arbitrarily and then use the above formula to successively compute new approximations. If we let
arbitrarily and then use the above formula to successively compute new approximations. If we let 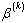 denote the approximation at the kth iteration, then the update formula can be expressed as:
denote the approximation at the kth iteration, then the update formula can be expressed as: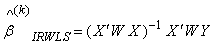
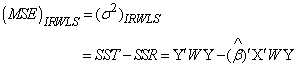
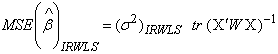
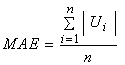
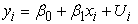
 was obtained from a set numbers (1, 1.1, 1.2, 1.3 ...),
was obtained from a set numbers (1, 1.1, 1.2, 1.3 ...), 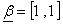 where, distribution of errors (normal, Contaminant, Laplace, Cauchy). And size of random: n=20, n=50, n=100 and n=200.
where, distribution of errors (normal, Contaminant, Laplace, Cauchy). And size of random: n=20, n=50, n=100 and n=200. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML