1. Introduction

Multicollinearity can cause serious problem in estimation and prediction when present in a set of predictors. Traditional statistical estimation procedures such as Ordinary Least Squares (OLS) tend to perform poorly, have high prediction variance, and may be difficult to interpret [1] i.e. because of its large variance’s and covariance’s which means the estimates of the parameters tend to be less precise and lead to wrong inferences [2] . In such situations it is often beneficial to use shrinkage i.e. shrink the estimator towards zero vector, which in effect involves introducing some bias so as to decrease the prediction variance, with the net result of reducing the mean squared error of prediction, they are nothing more than penalized estimators, due to estimation there is objective functions with the addition of a penalty which is based on the parameter. Various assumptions have been made in the literature where penalty of 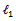- norm, 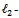norm or both 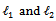which stand as tuning parameters 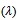were used to influence the parameter estimates in order to minimized the effect of the collinearity. Shrinkage methods are popular among the researchers for their theoretical properties e.g. parameter estimation.

Over the years, the LASSO - type methods have become popular methods for parameter estimation and variable selection due to their property of shrinking some of the model coefficients to exactly zero see [3], [4]. [3] Proposed a new shrinkage method Least Absolute Shrinkage and Selection Operator (LASSO) with tuning parameter 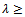0 which is a penalized method, [5] for the first systematic study of the asymptotic properties of Lasso – type estimators [4]. The LASSO shrinks some coefficients while setting others to exactly zero, and thus theoretical properties suggest that the LASSO potentially enjoys the good features of both subset selection and ridge regression. [6] had earlier proposed Ridge regression which minimizes the Residual Sum of Squares subject to constraint with

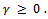[6] argued that the optimal choice of parameter 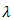yields reasonable predictors because it controls the degree of precision for true coefficient of 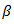to aligned with original variable axis direction in the predictor space. [7] Introduced the Smoothing Clipped Absolute Deviation (SCAD) which penalized Least Square estimate to reduce bias and satisfy certain conditions to yield continuous solutions. [8] was first to propose Ridge Regression which minimizes the Residual Sum of Squares subject to constraint with 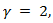thus regarded as 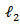- norm. [9] developed Least Angle Regression Selection (LARS) for a model selection algorithm [10], [11] study the properties of adaptive group Lasso. In 2006, [12] proposed a Generalization of LASSO and other shrinkage methods include Dantzig Selector with Sequential Optimization, DASSO [13], Elastic Net [14], Variable Inclusion and Selection Algorithm, VISA [15], (Adaptive LASSO [16] among others.

LASSO-type estimators are the techniques that are often suggested to handle the problem of multicollinearity in regression model. More often than none, Bayesian simulation with secondary data has been used. When the ordinary least squares are adopted there is tendency to have poor inferences, but with LASSO-type estimators which have recently been adopted may still come with its shortcoming by shrinking important parameters, we intend to examine how this shrink parameters may be affected asymptotically. However, the performances of other estimators have not been exhaustively compared in the presence of all these problems. Moreover, the question of which estimator is robust in the presence of a LASSO-type estimators of these problems have not been fully addressed. This is the focus of this research work.

2. Material and Method

Consider a simple least squares regression model.

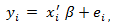(1)

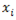where are exogenous, 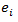are 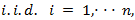random variable with mean zero and finite variance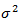 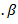is 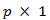vector. Suppose 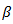takes the largest possible dimension , in other words the number of regressors may be at most 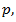but the true p is somewhere between 1 and 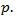The issue here is to come up with the true model and estimate it at the same time.

The least squares estimate without model selection is

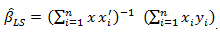with 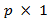estimates.

Shrinkage estimators are not that easy to calculate as least squares. Thus the objective functions for the shrinkage estimators:

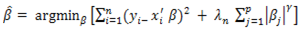(2)

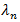Where is a tuning parameter (for penalization), it is a positive sequence, and 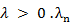will not be estimated, and 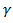will be specified by us. The objective function consists of 2 parts, the first one is the LS objective function part, and then the penalty factor.

Thus, taking the penalty part only

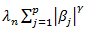If 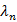is going to infinity or to a constant, the values of 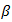that minimizes that part should be the case that 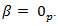We get all zeros if we minimize only the penalty part. So the penalty part will shrink the coefficients to zero. This is the function of the penalty.

Ridge Regression (RR) by [17] is ideal if there are many predictors, all with non-zero coefficients and drawn from a normal distribution [18] In particular, it performs well with many predictors each having small effect and prevents coefficients of linear regression models with many correlated variables from being poorly determined and exhibiting high variance. RR shrinks the coefficients of correlated predictors equally towards zero. So, for example, given k identical predictors, each would get identical coefficients equal to 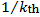the size that any one predictor would get if fit singly [18]. Ridge regression thus does not force coefficients to vanish and hence cannot select a model with only the most relevant and predictive subset of predictors. The ridge regression estimator solves the regression problem in [17] using 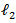penalized least squares:

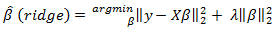(3)

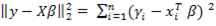Where is the –norm (quadratic) loss function (i.e. residual sum of squares), 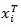is the 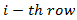of X, 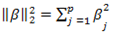is the 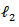– norm penalty on 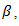and 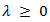is the tuning (penalty, regularization, or complexity) parameter which regulates the strength of the penalty (linear shrinkage) by determining the relative importance of the data-dependent empirical error and the penalty term. The larger the value of 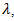the greater is the amount of shrinkage. As the value of 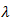is dependent on the data it can be determined using data-driven methods, such as cross-validation. The intercept is assumed to be zero in (3) due to mean centering of the phenotypes.

2.1. Least Absolute Shrinkage and Selection Operator (LASSO)

LASSO regression methods are widely used in domains with massive datasets, such as genomics, where efficient and fast algorithms are essential [18] .The LASSO is, however, not robust to high correlations among predictors and will arbitrarily choose one and ignore the others and break down when all predictors are identical [18]. The LASSO penalty expects many coefficients to be close to zero, and only a small subset to be larger (and nonzero).

The LASSO estimator [3] uses the 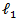penalized least squares criterion to obtain a sparse solution to the following optimization problem:

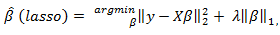(4)

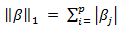Where is the 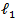-norm penalty on 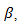which induces sparsity in the solution, and 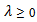is a tuning parameter.

The 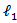penalty enables the LASSO to simultaneously regularize the least squares fit and shrinks some components of 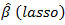to zero for some suitably chosen 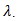The cyclical coordinate descent algorithm, [18], efficiently computes the entire lasso solution paths for 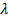for the lasso estimator and is faster than the well-known LARS algorithm [9]. These properties make the lasso an appealing and highly popular variable selection method.

2.2. Fused LASSO

To compensate the ordering limitations of the LASSO, [19] introduced the fused LASSO. The fused LASSO penalizes the 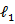-norm of both the coefficients and their differences:

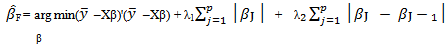(5)

where λ₁ and λ₂ are tuning parameters. They provided the theoretical asymptotic limiting distribution and a degrees of freedom estimator.

2.3. Elastic Net

[14] proposed the elastic net, a new regularization of the LASSO, for the unknown group of variables and for the multicollinear predictors. The elastic net method overcomes them limitations of the method which uses a penalty function based on

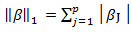Use of this penalty function has several limitations. For instance, in the "large p, small n" case the LASSO selects at most n variables before it saturates. Also if there is a group of highly correlated variables, then the LASSO tends to select one variable from a group and ignore the others. To overcome these limitations, the elastic net adds a quadratic part to the penalty 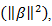which when used alone is (known also as ). The elastic net estimator can be expressed as

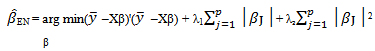(7)

where λ₁ and λ₂ are tuning parameters. As a result, the elastic net method includes the LASSO and ridge regression: in other words, each of them is a special case where

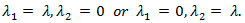
2.4. Adaptive LASSO

[7] showed that the LASSO can perform automatic variable selection but it produces biased estimates for the large coefficients. [16] introduced the adaptive LASSO estimator as

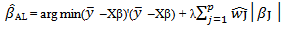(8)

Table 1. Mean AIC and BIC of the fitted model using the five methods

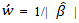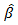with the weight vector where is a 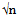consistent estimator such as 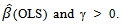where 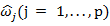are the adaptive data-driven weights, which can be estimated by, 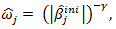where 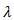is a positive constant and 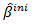is an initial consistent estimator of 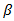obtained through least squares or ridge regression if multicollinearity is important [16]. The optimal value of 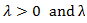can be simultaneously selected from a grid of values, with values of 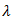selected from {0.5, 1, 2}, using two-dimensional cross-validation [16]. The weights allow the adaptive LASSO to apply different amounts of shrinkage to different coefficients and hence to more severely penalize coefficients with small values. The flexibility introduced by weighting each coefficient differently corrects for the undesirable tendency of the lasso to shrink large coefficients too much yet insufficiently shrink small coefficients by applying the same penalty to every regression coefficient [16].

3. Monte Carlo Study

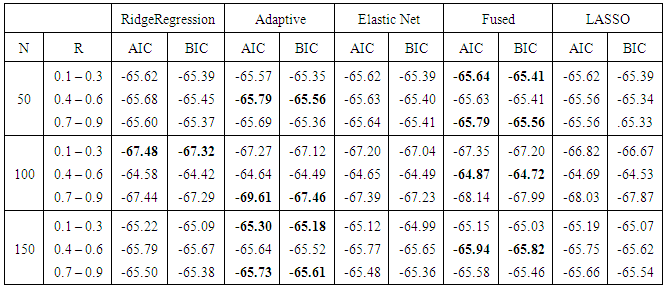
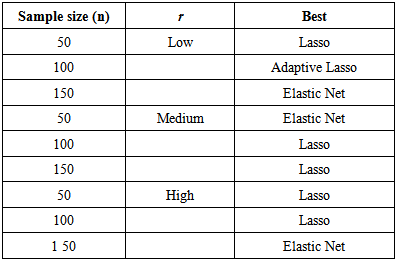
In this section we carried out simulation to examining the finite sample performance for LASSO, Adaptive LASSO, Elastic LASSO, Fused LASSO and Ridge Regression via AIC and BIC are compared. We infected the data with multicollinearity by generating sets of variables of sample sizes n (n = 50, 100 and 150) using normal distribution respectively. The level of multicollinearity among the variables are small (r = 0.1 – 0.3), mild (r = 0.4 – 0.6) and serious (r = 0.7 – 0.9). Each simulation was repeated 1000 times for consistency using R package.

Table 2. Summary of the result

Table 1 shows both the AIC and BIC of the fitted model using the five methods. It is of interest to note that both criteria agreed in selecting the best method in all the cases considered. It can be observed LASSO performed better at all the three levels of multicollinearity (small sample with low multicollinearity, medium sample size with medium multicollinearity and at small and medium sample sizes with high multicollinearity).

Elastic Net competed favourably with LASSO because it was also better at all levels of multicollinearity (high sample size with low multicollinearity, small sample size with medium multicollinearity and large sample size with high multicollinearity). Adaptive LASSO performed best only with medium sample size at low multicollinearity. Generally, it can be seen that LASSO performs best when the correlation is high but Elastic net tend to be more accurate when the sample size n is large. Conclusively, LASSO appears to have best overall performance among all the five methods considered (Table 2), therefore one can consider the LASSO method more suitable due to its significant advantage over others.

4. Conclusions

We have considered Lasso type estimator in the presence of multicollinearity in linear model due to Ordinary Least Squares (OLS) bring about poor parameters estimate and produce wrong inferences. Lasso type estimators are more stable likewise provide performances (outperforms) simple application of parameter estimator methods in the case of correlated predictors and produce sparser solution.