-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Statistics and Applications
p-ISSN: 2168-5193 e-ISSN: 2168-5215
2014; 4(4): 212-216
doi:10.5923/j.statistics.20140404.06
A Note on Estimability in Linear Models
1Department of Mathematics and Statistics, Federal Polytechnic, Nekede, Owerri, Imo State, Nigeria
2Department of Statistics, Imo State University, Owerri, Imo State, 460222, Nigeria
Correspondence to: S. O. Adeyemo, Department of Mathematics and Statistics, Federal Polytechnic, Nekede, Owerri, Imo State, Nigeria.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Estimable functions of the parameters are characterized in terms of generalized inverses. The concept of estimability is applied to data from a designed experiment on varietal trials. We demonstrate in this note that this technique of solving the normal equations is equivalent to the nearest neighbour method for the analysis of unbalanced randomized design.
Keywords: BLUE, Estimable Functions, Estimability, Generalized Inverses, Less than Full Rank, Linear Combination, Linear Models
Cite this paper: S. O. Adeyemo, F. N. Nwobi, A Note on Estimability in Linear Models, International Journal of Statistics and Applications, Vol. 4 No. 4, 2014, pp. 212-216. doi: 10.5923/j.statistics.20140404.06.
1. Introduction
- Linear models are generally of the form
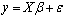 | (1) |
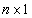 observation vector, X is an
observation vector, X is an 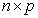 design matrix of fixed constants having rank r
design matrix of fixed constants having rank r 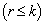 ,
, 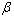 is an
is an 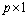 vector of unknown parameters,
vector of unknown parameters, 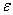 is an
is an 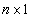 vector of unknown random errors having zero means) and
vector of unknown random errors having zero means) and 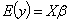 . The Ordinary Least Square (OLS) solution of (1) is
. The Ordinary Least Square (OLS) solution of (1) is 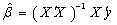 , a unique solution. In practice, not all linear models of the form in (1) are of full rank. When X is not of full rank, then
, a unique solution. In practice, not all linear models of the form in (1) are of full rank. When X is not of full rank, then 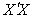 is singular and the normal equations
is singular and the normal equations 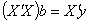 do not have a unique solution. However, there are various approaches of obtaining the inverse of singular matrices, for which the row echelon form given by Elswick et al (1991), Moore Penrose and the generalized inverse, Searle (1977) are popular in the literature. The generalized inverse is the approach we apply in this paper.
do not have a unique solution. However, there are various approaches of obtaining the inverse of singular matrices, for which the row echelon form given by Elswick et al (1991), Moore Penrose and the generalized inverse, Searle (1977) are popular in the literature. The generalized inverse is the approach we apply in this paper. 2. Form of Estimability
- With X less than full rank and
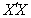 singular, i.e.
singular, i.e. 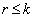 , there is an infinite number of solutions of
, there is an infinite number of solutions of 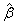 to the normal equations. Attention is therefore directed not to the solutions themselves but to linear functions of their elements. Consider a linear function
to the normal equations. Attention is therefore directed not to the solutions themselves but to linear functions of their elements. Consider a linear function 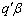 of the parameters in
of the parameters in 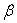 , where
, where 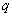 is a known vector. This linear function is defined as being an estimable function if there exists some linear combinations of the observations
is a known vector. This linear function is defined as being an estimable function if there exists some linear combinations of the observations 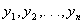 whose expected value is
whose expected value is 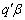 , i.e. if there exists a vector
, i.e. if there exists a vector 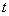 such that the expected value of
such that the expected value of 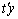 is
is 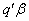 , then
, then 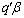 is said to be estimable. Consider the following theorem given in Graybill, 1976:Theorem 1. (Graybill, 1976)Assuming a linear model in (1),
is said to be estimable. Consider the following theorem given in Graybill, 1976:Theorem 1. (Graybill, 1976)Assuming a linear model in (1), 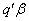 is an estimable function if and only if there exist an
is an estimable function if and only if there exist an 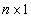 vector such that
vector such that 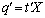 Proof. If there exist a vector such that
Proof. If there exist a vector such that 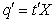 , then,
, then, 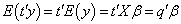 .Only if: Conversely, if
.Only if: Conversely, if 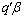 is estimable, then,
is estimable, then,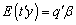 Thus
Thus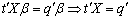 In addition, Elswick et al (1991) argues that if X is of full rank,
In addition, Elswick et al (1991) argues that if X is of full rank, 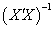 exists and the rows of
exists and the rows of 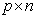 matrix
matrix 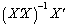 serve as the necessary set of vectors because
serve as the necessary set of vectors because 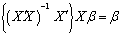
3. Illustration
- We demonstrate this discussion by considering the data from a study to compare classical and nearest neighbour methods in the analysis of varietal trials (See, e.g. Nwobi, 2000). In the experiment, nine (9) different varieties of cassava crop were tried, six at a time over a maximum of five years in such a way that these varieties were not replicated equally. The model (without interaction) is given by
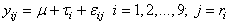 | (3) |
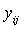 is the yield from the jth trial of the ith variety,
is the yield from the jth trial of the ith variety, 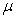 is the general mean,
is the general mean, 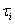 is the effect of the ith variety,
is the effect of the ith variety, 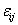 is the random error associated with
is the random error associated with 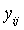 .Equation (3) is written in matrix form as
.Equation (3) is written in matrix form as 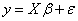 | (4) |
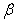 is given by
is given by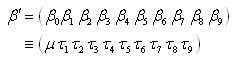 The components of the model (4) are
The components of the model (4) are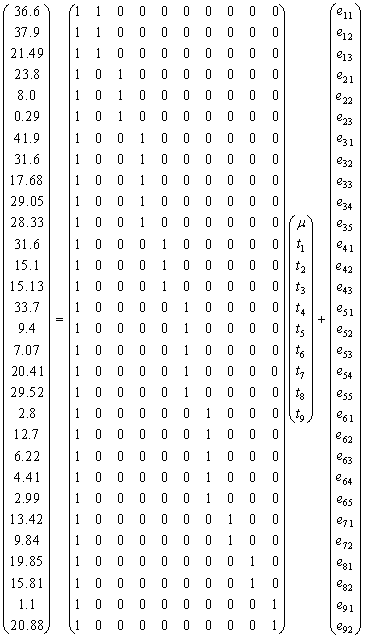 from where we obtain
from where we obtain A generalized inverse of
A generalized inverse of  written as
written as 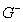 such that
such that 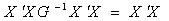 see, e.g. Searle (1977) is
see, e.g. Searle (1977) is  with
with and
and 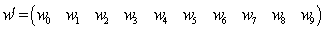 . The function
. The function 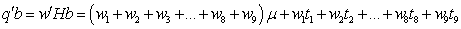 is estimable for any given values to the
is estimable for any given values to the 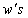 . With this we obtain the solution to the normal equation as
. With this we obtain the solution to the normal equation as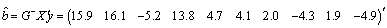 Therefore, the Best Linear Unbiased Estimator (BLUE) of
Therefore, the Best Linear Unbiased Estimator (BLUE) of 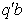 is
is 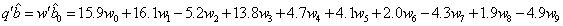 To see if
To see if 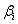 where
where 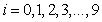 is estimable, we write the parameter as
is estimable, we write the parameter as 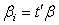 where, in this case, we define
where, in this case, we define 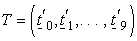 , a
, a 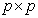 matrix;
matrix; 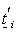 is of dimension
is of dimension 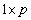 , so that
, so that
 Since
Since 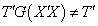 ,
, 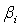 is not estimable. However, considering
is not estimable. However, considering 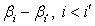 , this function may be written for
, this function may be written for 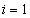 and
and 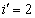 as
as 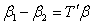 where
where 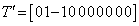 so that
so that 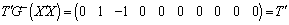 . This implies that
. This implies that 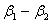 is estimable. Similarly, since there are 9 (nine) parameters, taking two (contrast) at a time gives
is estimable. Similarly, since there are 9 (nine) parameters, taking two (contrast) at a time gives 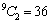 estimable functions
estimable functions Therefore,
Therefore, 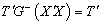 . Thus, we can say that a linear combination of estimable functions is estimable.
. Thus, we can say that a linear combination of estimable functions is estimable.4. Conclusions
- We have shown that for any arbitrary vector
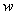 ,
, 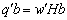 is estimable with BLUE
is estimable with BLUE 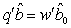 . The solution of the normal equation,
. The solution of the normal equation, 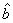 , confirms that this approach is equivalent to the Nearest Neighbour method of analysis of designed experiments. Both methods agree on the selection of varieties though the value of these estimates are not unique due to the application of generalized inverses. Furthermore, we verified that the linear combination of estimable functions is estimable.
, confirms that this approach is equivalent to the Nearest Neighbour method of analysis of designed experiments. Both methods agree on the selection of varieties though the value of these estimates are not unique due to the application of generalized inverses. Furthermore, we verified that the linear combination of estimable functions is estimable. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML