Abidoye A. O., Jolayemi E. T., Sanni O. O. M., Oyejola B. A.
Department of Statistics, University of Ilorin, Ilorin, Nigeria
Correspondence to: Abidoye A. O., Department of Statistics, University of Ilorin, Ilorin, Nigeria.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, we examined a test statistic for testing ordered alternative hypothesis under unequal group variances. The proposed modified t – test statistic obtained by replacing the pooled sample variance with the corresponding harmonic mean of variances in other to avoid the Behren – Fisher’s problem. The distribution of the sample of harmonic mean of variances which is known to be generalized Beta is approximated by the chi – square using a condition that is easily satisfied. The result shows that the modified t – test statistic is found to be appropriate for the data set obtained from Kwara Agricultural Development Project (KWADP) where the crop yields of the treatment means were known to be in a particular order because of ecological conditions.
Keywords:
Ordered alternative, ANOVA, Variances heterogeneity , Harmonic mean of variances
Cite this paper: Abidoye A. O., Jolayemi E. T., Sanni O. O. M., Oyejola B. A., Application of Harmonic Mean of Variances for Testing Ordered Alternative Hypothesis under Variance Heterogeneity, International Journal of Statistics and Applications, Vol. 4 No. 4, 2014, pp. 177-180. doi: 10.5923/j.statistics.20140404.01.
1. Introduction
This work primarily concerns itself with the application of test hypothesis with directional alternatives. This has application in many fields. For examples, there may be a number of cures for a particular ailment. Orthodox chemotherapy, non-orthodox herbal and “body cure” (allowing the body to perform the cure) may be three methods of cure. The best, in terms of duration of treatment before cure could be chemotherapy, followed by the herbal. Thus, if time to realize the cure is the concerned variable, then the means would be ordered from the shortest (obtained from orthodox) to the one obtained by herbs, while the time for body cure is the last. Several authors have provided adequate literature in this area of Analysis of Variance such as Ott (1984), Montgomery (1981) amongst. Many authors have also developed method of testing of homogeneity of means. Such authors include Jonckheere (1954), Bartholomew (1959), Yahya and Jolayemi (2003), Dunnett (1964), Barlow et. al (1971), Dunnett (1980), Dunnett and Tamhane (1997), Keselman and Wilox (1999), Gupta et al (2006), Abidoye et. al (2013a), (2013b), (2013c) and several others.
2. Development of the Test Procedure
In this section we are interested in developing a suitable test procedure to test the hypothesis against ordered means which is given by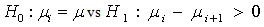 | (2.1) |
[The situation in which the hypothesis set is given as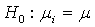 vs
vs 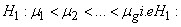
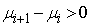 can also be handed similarly]When
can also be handed similarly]When 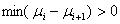 then the alternative hypothesis is sustained. In this formulation then,
then the alternative hypothesis is sustained. In this formulation then, 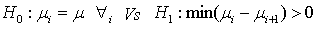 | (2.2) |
Now assume that 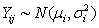 and identically and independently distributed where
and identically and independently distributed where 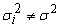 for at least one i, i =1, 2, …, g, j = 1, 2, …, ni The unbiased estimate of
for at least one i, i =1, 2, …, g, j = 1, 2, …, ni The unbiased estimate of 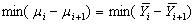 | (2.3) |
and that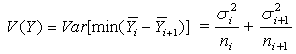 | (2.4) |
so that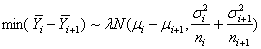 | (2.5) |
where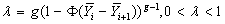 | (2.6) |
obtained from order statistics, from equation (2.5), 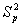 will be appropriate to be used as the estimate if the group of variances are equal, i.e
will be appropriate to be used as the estimate if the group of variances are equal, i.e 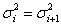
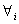 where
where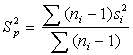 Consider the observations
Consider the observations  in which there exists at least one outlier. Within this situation it is a well known fact that sample mean
in which there exists at least one outlier. Within this situation it is a well known fact that sample mean 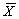 given as
given as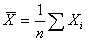 is not a good location summary. Instead, the Harmonic mean
is not a good location summary. Instead, the Harmonic mean 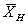 given by
given by 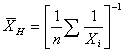 is a better choice. Similarly let
is a better choice. Similarly let 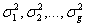 be the variances of the g groups
be the variances of the g groups 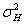 which is the Harmonic mean of the variances is a better choice whenever at least one
which is the Harmonic mean of the variances is a better choice whenever at least one 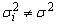 .Note that
.Note that 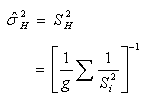 see abidoye et. al (2012, 2013a and 2013b)But in a situation where the group variances are not equal, that is,
see abidoye et. al (2012, 2013a and 2013b)But in a situation where the group variances are not equal, that is, 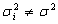 for at least one
for at least one 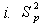 (pooled variance which is the weighted mean of variances) can not be used. This is the Behren’s – Fisher problem.Thus
(pooled variance which is the weighted mean of variances) can not be used. This is the Behren’s – Fisher problem.Thus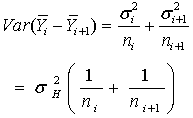 The test statistic for the hypotheses set in (2.2) is therefore
The test statistic for the hypotheses set in (2.2) is therefore 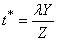 | (2.7) |
where 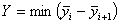 | (2.8) |
and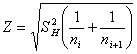 | (2.9) |
where 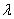 is the appropriate normalization from order statistics. The null hypothesis is then rejected if
is the appropriate normalization from order statistics. The null hypothesis is then rejected if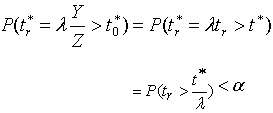 | (2.10) |
where tr is the regular t – distribution with r d.f is given by because 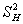 has approximately the
has approximately the 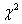 - distribution with the degree of freedom r to be determined from r = 22.096 + 0.266(n-g) - 0.000029
- distribution with the degree of freedom r to be determined from r = 22.096 + 0.266(n-g) - 0.000029 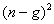 . See Abidoye (2012) and Abidoye et. al 2013a. If the alternative hypothesis (H1) in equation (2.10) is reversed.Then
. See Abidoye (2012) and Abidoye et. al 2013a. If the alternative hypothesis (H1) in equation (2.10) is reversed.Then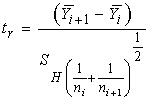 | (2.12) |
3. Application of the Test Procedure
Practical situations where this test procedure is applicable are presented in this section. The data on Maize was found in Kwara Agricultural Development Project (KWADP), Ilorin, Kwara State for the period of 1998 to 2007. By KWADP standard, Kwara State has been categorized into four major unique ecological zones based on the climatic and ecological differences.
3.1. Example on Maize Yields in Kwara State
Consider the data on yields of maize (in Tonnes per hectare) given by KWADP who believed that crop yield in the area under consideration, zone D has the highest yield followed by zone A, then zone C and zone B with the least yield.If 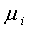 represents the mean population yield of maize in zone i where
represents the mean population yield of maize in zone i where 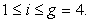 Let
Let 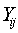 represents the crop (maize) yield (in Tonnes per hectare) in zone i for year j, i = 1, 2, 3, 4 ; j=1, 2, …, 10.Then, assume
represents the crop (maize) yield (in Tonnes per hectare) in zone i for year j, i = 1, 2, 3, 4 ; j=1, 2, …, 10.Then, assume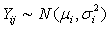 | (2.13) |
First it is necessary to examine the values of the group variances. This was done in Table 3.1, confirming unexqual variances.Table 3.1. Spss Result Output on Test of Homogeneity of Variances For Maize
 |
| |
|
The hypothesis to be tested is 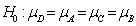 Vs
Vs 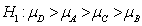 ;
; 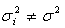 for at least one iThe Proposed Test Statistic is
for at least one iThe Proposed Test Statistic is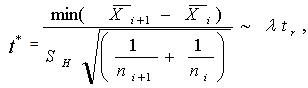 where
where 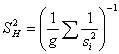 and
and 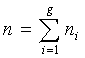 The null hypothesis, H0 is rejected at specified α level of significance ifP-value =
The null hypothesis, H0 is rejected at specified α level of significance ifP-value = 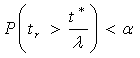 , where
, where 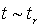 COMPUTATION ON MAIZEFrom the data on Maize yield the following summary statistics were obtained:Zone A:
COMPUTATION ON MAIZEFrom the data on Maize yield the following summary statistics were obtained:Zone A: 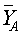 =1.014,
=1.014, 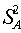 =0.056,
=0.056, 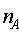 =10Zone B:
=10Zone B: 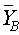 =0.618,
=0.618, 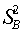 =0.0126,
=0.0126, 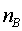 =10Zone C:
=10Zone C: 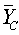 =0.8,
=0.8, 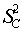 =0.0111,
=0.0111, 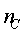 =10Zone D:
=10Zone D: 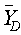 =2.776,
=2.776, 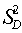 =0.027,
=0.027, 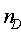 =10Therefore,
=10Therefore, Then consider the differences given below:
Then consider the differences given below: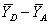 = 2.776 - 1.014 = 1.762
= 2.776 - 1.014 = 1.762 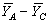 = 1.014 - 0.80 = 0.214
= 1.014 - 0.80 = 0.214 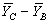 = 0.80 - 0.618 = 0.182
= 0.80 - 0.618 = 0.182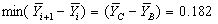 with
with 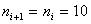 , g = 4
, g = 4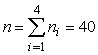
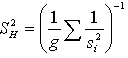
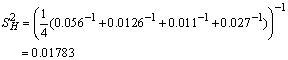
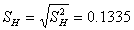
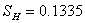
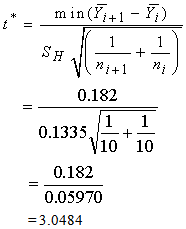 where r = 22.096 + 0.266(n-g) - 0.000029
where r = 22.096 + 0.266(n-g) - 0.000029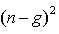 = 31.634
= 31.634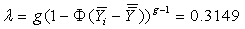 , 0 < λ< 1 from equation (2.1)
, 0 < λ< 1 from equation (2.1) 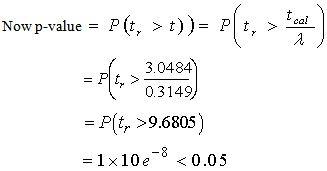 Which led to the rejection of H0 and conclude that the mean yields of maize in all the four zones were indeed ordered from D, A, C, B..
Which led to the rejection of H0 and conclude that the mean yields of maize in all the four zones were indeed ordered from D, A, C, B..
4. Conclusions
In this study, we examined a test statistic for testing ordered alternative hypothesis under unequal variances. We proposed a modified t – test statistic, the harmonic mean of the variances to replace the sample pooled variance so as to avoid the Beheren – Fisher’s problem. Because the sample harmonic mean of variances has the chi – square distribution, then the modified t – statistic is found to be appropriate for the data set used from Kwara Agricultural development project (KWADAP).
References
| [1] | Abidoye, A. O (2012): Development of Hypothesis Testing Technique for Ordered Alternatives under heterogeneous variances. Unpublished Ph.D Thesis submitted to Dept. of Statistics, University of Ilorin, Ilorin. |
| [2] | Abidoye, A.O, Jolayemi, E.T, Sanni, O.O.M and Oyejola, B.A (2013a): On Hypothesis Testing Under Unequal Group Variances: The Use of the Harmonic variance. The International Journal of Institute for science, Technology and Education. Vol. 3, No 7, Page 11 – 15. |
| [3] | Abidoye, A.O, Jolayemi, E.T, Sanni, O.O.M and Oyejola, B.A (2013b): Development of a Test statistic for Testing Equality of Two Means Under Unequal Population Variances. The International Journal of Institute for science, Technology and Education. Vol. 3, No 10, page 10 -14. |
| [4] | Abidoye, A.O, Jolayemi, E.T, Sanni, O.O.M and Oyejola, B.A (2013c): Development of a Test Statistic for Testing Equality of Means Under Unequal Population Variances. The International Journal of Mathematics and Statistics Invention. Vol. 1, page 38 -43. |
| [5] | Barlow, R.E, Bartholomew, D.J, Bremmer, J.M and Brunk, H.D (1971): “Statistical Inference under Order Restrictions: The Theory and Application of Isotonic Regression.” Wiley, New York. |
| [6] | Bartholomew, D.J (1959): “A test of homogeneity for ordered alternative.” Biometrica, 46, 3648. |
| [7] | Dunnett, C. W and Tamhane, A. C (1997): Multiple testing to establish superiority / equivalence of a new treatment compare with k standard treatments. Statistics in Medicine 16, 2489 – 2506. |
| [8] | Dunnett , C. W (1964): New tables for multiple comparison with a control. Biometric, 20, 482-491. |
| [9] | Dunnett, C.W (1980): “Pairwise multiple comparison in the homogeneous variance, unequal sample size case” Journal of the American Statistical Association. 75, 789 – 795. |
| [10] | Gupta, A.K, Solomon, W.H and Yasunori, F (2006): Asymptotics for testing hypothesis In some Multivariate variance components model Under non-normality. Journal of Multivariate Analysis archive. Vol. 97, pp 148-178. |
| [11] | Jonckheere, A.R (1954): “A distribution-free k-sample test against ordered alternative.” Biometrical, 41, 133-145. |
| [12] | Keselman, H.J and Wilcox R. (1999): The Improved Brown and Forsythe test for mean equality: Some things can’t be fixed. Communications in Statistics – Simulation and Computations, Vol. 28, Pages 687- 698. |
| [13] | Montgomery, D.C (1981): “Design and Analysis of Experiment.” Second Edition. John Wiley and sons Inc. New York. |
| [14] | Ott, L (1984): “An Introduction To Statistical Methods and Data Analysis”. Second edition. P.W.S Publisher. Boston. |
| [15] | Yahya, W.B and Jolayemi, E.T (2003): Testing Ordered Means against a Control. JNSA, 16, 40-51. |

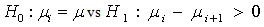
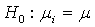 vs
vs 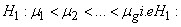
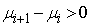 can also be handed similarly]When
can also be handed similarly]When 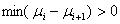 then the alternative hypothesis is sustained. In this formulation then,
then the alternative hypothesis is sustained. In this formulation then, 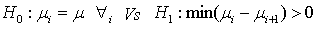
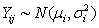 and identically and independently distributed where
and identically and independently distributed where 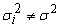 for at least one i, i =1, 2, …, g, j = 1, 2, …, ni The unbiased estimate of
for at least one i, i =1, 2, …, g, j = 1, 2, …, ni The unbiased estimate of 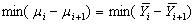
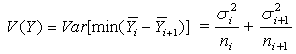
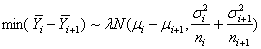
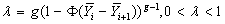
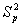 will be appropriate to be used as the estimate if the group of variances are equal, i.e
will be appropriate to be used as the estimate if the group of variances are equal, i.e 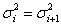
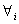 where
where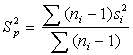 Consider the observations
Consider the observations  in which there exists at least one outlier. Within this situation it is a well known fact that sample mean
in which there exists at least one outlier. Within this situation it is a well known fact that sample mean 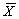 given as
given as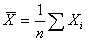 is not a good location summary. Instead, the Harmonic mean
is not a good location summary. Instead, the Harmonic mean 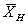 given by
given by 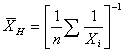 is a better choice. Similarly let
is a better choice. Similarly let 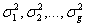 be the variances of the g groups
be the variances of the g groups 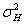 which is the Harmonic mean of the variances is a better choice whenever at least one
which is the Harmonic mean of the variances is a better choice whenever at least one 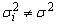 .Note that
.Note that 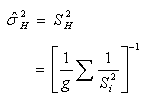 see abidoye et. al (2012, 2013a and 2013b)But in a situation where the group variances are not equal, that is,
see abidoye et. al (2012, 2013a and 2013b)But in a situation where the group variances are not equal, that is, 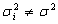 for at least one
for at least one 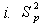 (pooled variance which is the weighted mean of variances) can not be used. This is the Behren’s – Fisher problem.Thus
(pooled variance which is the weighted mean of variances) can not be used. This is the Behren’s – Fisher problem.Thus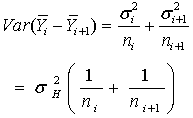 The test statistic for the hypotheses set in (2.2) is therefore
The test statistic for the hypotheses set in (2.2) is therefore 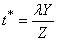
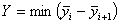
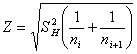
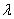 is the appropriate normalization from order statistics. The null hypothesis is then rejected if
is the appropriate normalization from order statistics. The null hypothesis is then rejected if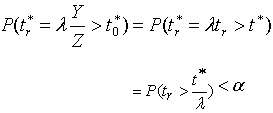
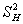 has approximately the
has approximately the 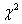 - distribution with the degree of freedom r to be determined from r = 22.096 + 0.266(n-g) - 0.000029
- distribution with the degree of freedom r to be determined from r = 22.096 + 0.266(n-g) - 0.000029 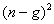 . See Abidoye (2012) and Abidoye et. al 2013a. If the alternative hypothesis (H1) in equation (2.10) is reversed.Then
. See Abidoye (2012) and Abidoye et. al 2013a. If the alternative hypothesis (H1) in equation (2.10) is reversed.Then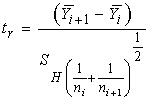
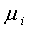 represents the mean population yield of maize in zone i where
represents the mean population yield of maize in zone i where 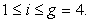 Let
Let 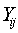 represents the crop (maize) yield (in Tonnes per hectare) in zone i for year j, i = 1, 2, 3, 4 ; j=1, 2, …, 10.Then, assume
represents the crop (maize) yield (in Tonnes per hectare) in zone i for year j, i = 1, 2, 3, 4 ; j=1, 2, …, 10.Then, assume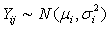
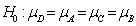 Vs
Vs 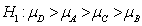 ;
; 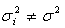 for at least one iThe Proposed Test Statistic is
for at least one iThe Proposed Test Statistic is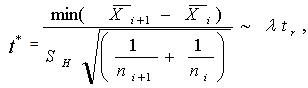 where
where 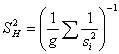 and
and 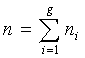 The null hypothesis, H0 is rejected at specified α level of significance ifP-value =
The null hypothesis, H0 is rejected at specified α level of significance ifP-value = 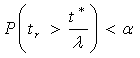 , where
, where 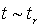 COMPUTATION ON MAIZEFrom the data on Maize yield the following summary statistics were obtained:Zone A:
COMPUTATION ON MAIZEFrom the data on Maize yield the following summary statistics were obtained:Zone A: 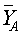 =1.014,
=1.014, 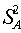 =0.056,
=0.056, 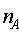 =10Zone B:
=10Zone B: 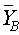 =0.618,
=0.618, 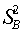 =0.0126,
=0.0126, 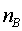 =10Zone C:
=10Zone C: 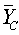 =0.8,
=0.8, 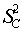 =0.0111,
=0.0111, 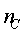 =10Zone D:
=10Zone D: 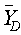 =2.776,
=2.776, 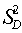 =0.027,
=0.027, 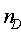 =10Therefore,
=10Therefore, Then consider the differences given below:
Then consider the differences given below: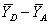 = 2.776 - 1.014 = 1.762
= 2.776 - 1.014 = 1.762 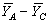 = 1.014 - 0.80 = 0.214
= 1.014 - 0.80 = 0.214 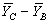 = 0.80 - 0.618 = 0.182
= 0.80 - 0.618 = 0.182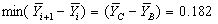 with
with 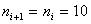 , g = 4
, g = 4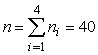
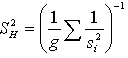
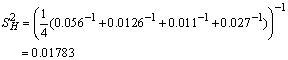
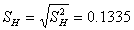
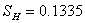
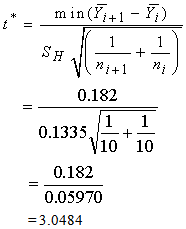 where r = 22.096 + 0.266(n-g) - 0.000029
where r = 22.096 + 0.266(n-g) - 0.000029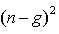 = 31.634
= 31.634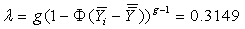 , 0 < λ< 1 from equation (2.1)
, 0 < λ< 1 from equation (2.1) 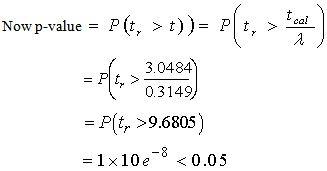 Which led to the rejection of H0 and conclude that the mean yields of maize in all the four zones were indeed ordered from D, A, C, B..
Which led to the rejection of H0 and conclude that the mean yields of maize in all the four zones were indeed ordered from D, A, C, B.. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML