Ijomah Maxwell Azubuike1, Opabisi Adeyinka Kosemoni2
1Dept. of Mathematics/Statistics, University of Port Harcourt, Rivers State
2Dept. of Mathematics/Statistics, Federal Polytechnic Nekede, Owerri Imo State
Correspondence to: Opabisi Adeyinka Kosemoni, Dept. of Mathematics/Statistics, Federal Polytechnic Nekede, Owerri Imo State.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Cross product matrix approach is a more widely used least-squares technique in estimating parameters of a multiple linear regression. However, it is imperative to consider other forms of estimating these parameters. The use of singular value decomposition as an alternative to the widely known cross-product matrix approach as formed one of the basis of discussion in this paper. However, the use of cross product matrix have placed a lot of restrictions on the user of this technique which makes it difficult to estimate parameter values when the predictor variables seem to be highly correlated, this is often the case when Collinearity (Multi-collinearity) exists among the predictor variables. The consequence of this is that certain conditions that makes the cross product matrix applicable are not satisfied, hence the singular value decomposition approach enables users to resolve this difficult. With the aid of empirical data sets, both methods have been compared and difficulties encountered in the use of the former have been resolved using the latter.
Keywords:
Singular Value Decomposition, Cross product and Collinearity
Cite this paper: Ijomah Maxwell Azubuike, Opabisi Adeyinka Kosemoni, Singular Value Decomposition Compared to cross Product Matrix in an ill Conditioned Regression Model, International Journal of Statistics and Applications, Vol. 4 No. 2, 2014, pp. 124-133. doi: 10.5923/j.statistics.20140402.07.
1. Introduction
The use of cross product matrix for obtaining least squares estimates in multiple regression analysis has been in use for a long time. It is about the major statistical technique for “fitting equations to data”. However, recent works has also provided modifications of the techniques aimed at increasing its reliability as a data-analytic tool most especially when near-collinearity exists between explanatory variables. When perfect collinearity occurs, the model can be reformulated in an appropriate fashion. A different type of problem occurs when collinearity is near perfect Belsley et al (1980). Collinearity can increase estimates of parameter variance; yield models in which no variable is statistically significant even when the correlation coefficient is large; produce parameter estimates of the “incorrect sign” and of implausible magnitude; create situations in which small changes in the data produce wide swings in parameter estimates; and, in truly extreme cases, prevent the numerical solution of a model. These problems can be severe and sometimes crippling. Rolf (2002), stated that mathematically, exact collinearities can be eliminated by reducing the number of variables, and near-collinearities can be made to disappear by forming new, orthogonalized and rescaled variables. However, omitting a perfect confounder from the model can only increase the risk for misinterpretation of the influences on the response variable. Replacing an explanatory variable by its residual, in a regression on the others from a set of near-collinear variables, makes the new variable orthogonal to the others, but with comparatively very little variability. Owing to this lack of substantial variability, we are not likely to see much of its possible influence. Mathematical rescaling cannot change this reality, of course. To a large extent it is a matter of judgment what should be called a comparatively large or small variation in different variables and variable combinations, and this ambiguity remains when it comes to shrinkage methods for predictor construction, because these are not invariant under individual rescaling and other non-orthogonal transformations of variables. We could say that the ‘near’ in near-collinearity is not scale invariant.The purpose of this paper is to compare the singular value decomposition to that of cross product matrix approach in an ill conditioned regression in order to observe if both approaches vary according to the degree of collinearity among the explanatory variables. The rest of this paper is organized as follows: Section two discusses the methodology, Section three discusses the data analysis and results while concluding remarks are presented in Section four.
2. Methodology
The cross-product matrix least-squares estimates approach and singular value decomposition will be employed in obtaining the parameters of the model. A comparison of the two approaches will be looked into with a view of observing if the two approaches will enable us obtain the equal parameter estimates.The general linear model assumes the form 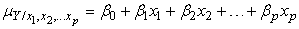 | (1) |
This model can also be written in the form 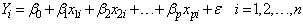 | (2) |
2.1. Cross-Product Matrix Approach for Obtaining Parameter Estimates
From equation (1) we form the equation below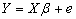 | (3) |
where 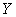 is a
is a  column vector of responses variable,
column vector of responses variable, 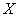 is
is 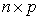 matrix of
matrix of 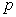 predictor variables of
predictor variables of 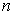 observations,
observations, 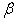 is a
is a 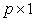 column vector and
column vector and 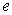 is a random error of
is a random error of 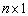 dimension associated with
dimension associated with 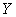 vector. Y and X are known vectors (observations obtained from a data set), while
vector. Y and X are known vectors (observations obtained from a data set), while 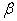 and
and 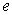 are unknown vectors.As defined earlier the vectors;
are unknown vectors.As defined earlier the vectors;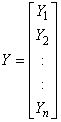 | (4) |
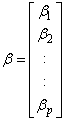 | (5) |
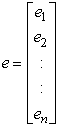 | (6) |
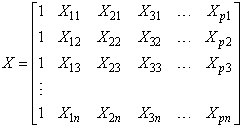 | (7) |
From equation (2) the unknown vectors 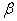 and
and 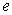 will be obtained using the cross-product matrix; Therefore we rewrite (2) since E(e)=0 (Regression Analysis Assumption)
will be obtained using the cross-product matrix; Therefore we rewrite (2) since E(e)=0 (Regression Analysis Assumption)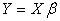 | (8) |
Multiplying both sides of equation (8) by 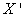
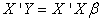 | (9) |
From equation (9) we form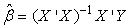 | (10) |
Equation (10) forms matrices for obtaining the estimates of the parameters. | (11) |
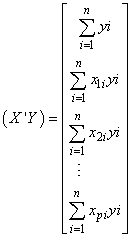 | (12) |
From equation (10) it can be established that 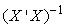 is the variance/co-variance matrix of the parameters, which is a useful in testing hypotheses and constructing of confidence intervals.
is the variance/co-variance matrix of the parameters, which is a useful in testing hypotheses and constructing of confidence intervals.
2.2. Singular Value Decomposition Approach
Given 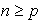 matrix X as earlier defined, it is possible to express each element
matrix X as earlier defined, it is possible to express each element  in the following way:
in the following way: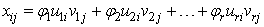 | (13) |
Hence by relation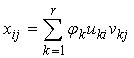 | (14) |
where 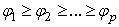 Equation (14) is known as the singular value decomposition (SVD) of matrix X. The number of terms in (15) is r which is the rank of matrix X; r cannot exceed n or p whichever is smaller.It is assumed that
Equation (14) is known as the singular value decomposition (SVD) of matrix X. The number of terms in (15) is r which is the rank of matrix X; r cannot exceed n or p whichever is smaller.It is assumed that 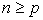 , and it follows that
, and it follows that 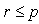 . The r vectors u are orthogonal to each other, as are the r vectors v. Furthermore, each of these vectors has unit length so that;
. The r vectors u are orthogonal to each other, as are the r vectors v. Furthermore, each of these vectors has unit length so that;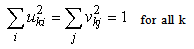 | (15) |
In matrix notation we have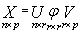 | (16) |
The matrix 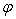 is diagonal, and all
is diagonal, and all 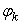 are positive. The columns of the matrix U are the u vectors, and the rows of V’ are the v vectors of (12). The orthogonality of the u and v and their unit length implies the conditions
are positive. The columns of the matrix U are the u vectors, and the rows of V’ are the v vectors of (12). The orthogonality of the u and v and their unit length implies the conditions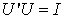 | (17) |
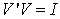 | (18) |
The 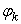 can be shown to be the square roots of the non zero eigenvalues of the square matrix
can be shown to be the square roots of the non zero eigenvalues of the square matrix 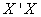 as well as the square matrix
as well as the square matrix 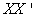 . The columns of U are the eigenvectors of
. The columns of U are the eigenvectors of 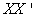 and the rows of V’ are the eigenvectors of
and the rows of V’ are the eigenvectors of 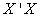 . When
. When 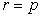 it is known as a full-rank case. Each element of X is easily reconstructed by multiplying the corresponding elements of the
it is known as a full-rank case. Each element of X is easily reconstructed by multiplying the corresponding elements of the 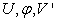 matrices and summing the terms.From equation (3)
matrices and summing the terms.From equation (3) 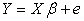 We obtain
We obtain 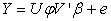 | (19) |
Can be expressed also as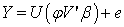 Where
Where 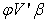 is a
is a 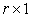 matrix, that is a vector of r elements. Let us denote the vector by
matrix, that is a vector of r elements. Let us denote the vector by 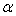 .
.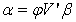 | (20) |
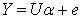 | (21) |
The matrix Y and the matrix U are known. The least squares solution for the unknown coefficients 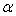 is obtained by the usual matrix equation
is obtained by the usual matrix equation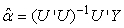 which, as a result of (17) becomes
which, as a result of (17) becomes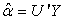 | (22) |
This equation is easily solved since 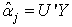 simply the inner product of the matrix Y with jth vector
simply the inner product of the matrix Y with jth vector 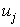 . It follows from (21) that
. It follows from (21) that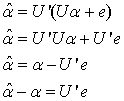 But E
But E 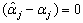
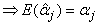 | (23) |
Thus, 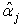 is unbiased. Furthermore, the variance of
is unbiased. Furthermore, the variance of 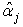 is
is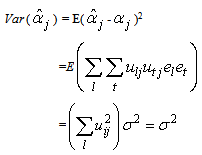 Hence
Hence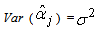 | (24) |
Therefore the relationship between 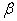 and
and 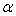 is given by equation (20), which also holds for the least squares estimates of
is given by equation (20), which also holds for the least squares estimates of 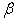 and
and 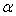
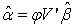 | (25) |
In (25), 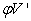 has the dimension
has the dimension 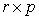 . Thus, given the
. Thus, given the 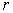 values of
values of 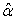 , the matrix relation (25) represents r equations in p unknown parameter estimates
, the matrix relation (25) represents r equations in p unknown parameter estimates 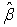 . If r=p (the full-rank case). The solution is possible and unique.In this case V’ is a
. If r=p (the full-rank case). The solution is possible and unique.In this case V’ is a 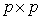 orthogonal matrix.Hence, the solution is given by
orthogonal matrix.Hence, the solution is given by 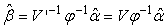 | (26) |
It will be noted that 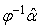 is
is 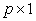 vector, obtained by dividing each
vector, obtained by dividing each 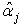 by the corresponding
by the corresponding 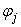 .An important use of (26) aside from its supplying the estimates of
.An important use of (26) aside from its supplying the estimates of 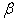 as functions of
as functions of 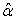 , is the ready calculation of the variances of the
, is the ready calculation of the variances of the 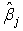 . In general notation this equation is written as
. In general notation this equation is written as 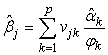 | (27) |
Also since the 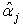 are mutually orthogonal and have all variances
are mutually orthogonal and have all variances 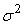 we see that
we see that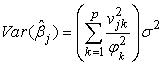 | (28) |
The numerators in each term are the squares of the elements in the first row of the V matrix and the denominators are the squares of 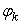 .
.
3. Data Analysis and Discussion
To simplify this exposition, we will consider the data below; which is on the details of measurements taken on 22 adults on lean body mass with height, body mass index and age given in the table below;Table 1
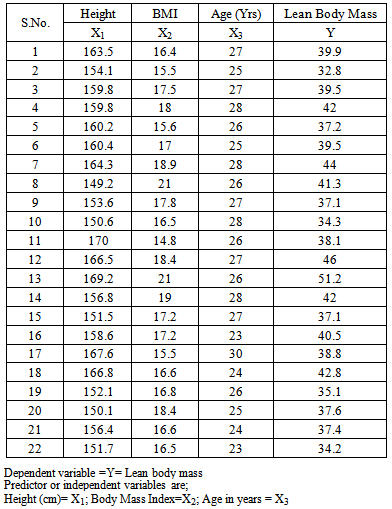 |
| |
|
3.1. Application of Cross-Product Matrix Approach
From equations (7and 4) we define the matrices
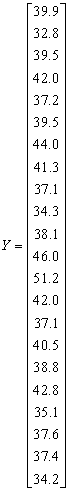 From equation (9) we obtain the cross-product of matrices
From equation (9) we obtain the cross-product of matrices 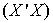 and
and 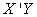 , Using MATLAB
, Using MATLAB 
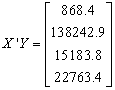 We then obtain
We then obtain 
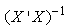 is the variance/co-variance matrix.
is the variance/co-variance matrix.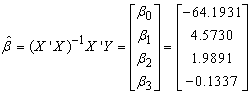
3.2. Singular Value Decomposition Approach
From equation (16) 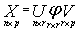 Matrix X as defined earlier;Using MATLAB we obtain the Matrices
Matrix X as defined earlier;Using MATLAB we obtain the Matrices 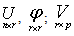 For U (see appendix)
For U (see appendix) Therefore, if
Therefore, if 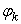 is the square roots of the non-zero eigen-values of the square matrix
is the square roots of the non-zero eigen-values of the square matrix 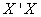 as well as the square matrix
as well as the square matrix 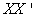 .The eigen-values of matrix
.The eigen-values of matrix  using MATLAB is obtained below
using MATLAB is obtained below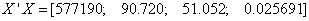 Redefining the Matrix
Redefining the Matrix 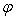 by leaving the non-zero vectors; we have
by leaving the non-zero vectors; we have Similarly, the columns U are the eigen-vectors of
Similarly, the columns U are the eigen-vectors of 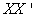 and the rows of V’ are the eigen-vectors of
and the rows of V’ are the eigen-vectors of 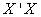 .To obtain the parameter estimates, from equation (26)
.To obtain the parameter estimates, from equation (26)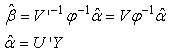 Where
Where 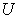 can be re-defined as column vectors U obtained from SVD (
can be re-defined as column vectors U obtained from SVD (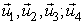 ) since r = 4, using MATLAB we have
) since r = 4, using MATLAB we have
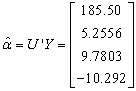 Similarly,
Similarly, 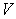 can be re-defined as row vectors V’ obtained from SVD (
can be re-defined as row vectors V’ obtained from SVD (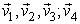 ) since r=4, using MATLAB we have
) since r=4, using MATLAB we have  Recall
Recall 

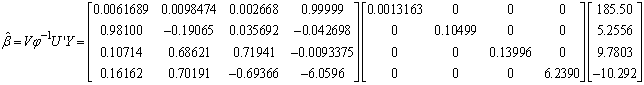
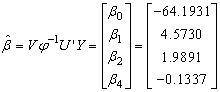 Similarly, obtaining the variances we have;
Similarly, obtaining the variances we have;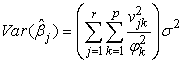 Using MATLAB
Using MATLAB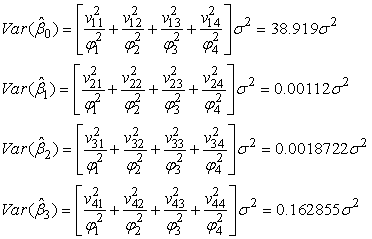 For obtaining co-variances we have;
For obtaining co-variances we have;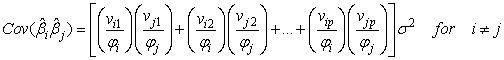 In general we have;
In general we have;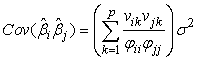
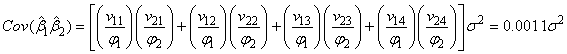
3.3. Cross Product Matrix Approach Versus Singular Value Decomposition
We have been able to obtain regression model parameter estimates using both procedures and results are the same in both cases. However, one question most users of cross product matrix might ask is why go through the trouble of decomposing your predictor variables to several matrices when similar estimates are obtainable? The user of cross product matrix must bear in mind that estimates are only obtainable if and only if 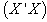 matrix is nonsingular (i.e
matrix is nonsingular (i.e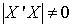 ). This is not often the case when predictor variables are linearly related, a situation often referred to as Perfect Collinearity or ill condition regression model.It then follows that, when
). This is not often the case when predictor variables are linearly related, a situation often referred to as Perfect Collinearity or ill condition regression model.It then follows that, when 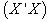 is singular, we can use SVD to approximate its inverse by the following matrix;
is singular, we can use SVD to approximate its inverse by the following matrix;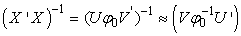 | (29) |
where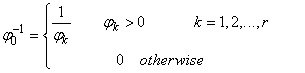 Equation (29) is a modified form of equation (16).
Equation (29) is a modified form of equation (16).
4. Conclusions
From the analysis carried out using the cross product matrix and Singular value decomposition approach, parameter estimates are easy and uniquely determined using the cross product approach when there exist no near-collinearity between explanatory variables. On the other hand, singular value decomposition enables us to obtain similar estimates when no near-collinearity between explanatory variables though requires much more computational techniques than cross product matrix approach, but in addition, it enables us to handle the case of near-collinearity between the explanatory variables or ill conditioned regression models by applying the use of SVD to the matrix 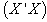 thus making it possible for users of the cross product matrix approach to obtain parameter estimates after obtaining the inverse of SVD of the matrix
thus making it possible for users of the cross product matrix approach to obtain parameter estimates after obtaining the inverse of SVD of the matrix 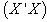 .
.
APPENDIX

References
| [1] | Belsley D.A., Kuh E.; and Welsch,R.E. (1980), Identifying Influential Data and Sources of Collinearity, New York: John Wiley. |
| [2] | Rolf S., (2002), Collinearity, Encyclopedia of Environmetrics, John Wiley & Sons, Ltd, Chichester, 1, 365 – 366. |

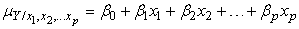
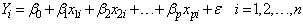
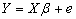
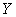 is a
is a  column vector of responses variable,
column vector of responses variable, 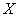 is
is 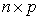 matrix of
matrix of 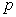 predictor variables of
predictor variables of 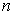 observations,
observations, 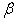 is a
is a 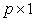 column vector and
column vector and 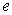 is a random error of
is a random error of 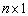 dimension associated with
dimension associated with 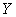 vector. Y and X are known vectors (observations obtained from a data set), while
vector. Y and X are known vectors (observations obtained from a data set), while 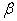 and
and 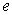 are unknown vectors.As defined earlier the vectors;
are unknown vectors.As defined earlier the vectors;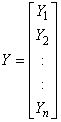
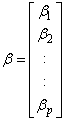
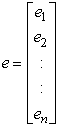
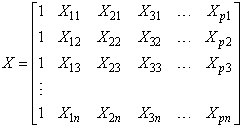
 and
and  will be obtained using the cross-product matrix; Therefore we rewrite (2) since E(e)=0 (Regression Analysis Assumption)
will be obtained using the cross-product matrix; Therefore we rewrite (2) since E(e)=0 (Regression Analysis Assumption)
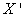
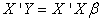
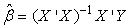

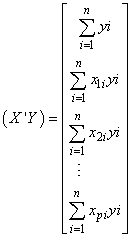
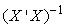 is the variance/co-variance matrix of the parameters, which is a useful in testing hypotheses and constructing of confidence intervals.
is the variance/co-variance matrix of the parameters, which is a useful in testing hypotheses and constructing of confidence intervals.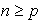 matrix X as earlier defined, it is possible to express each element
matrix X as earlier defined, it is possible to express each element  in the following way:
in the following way: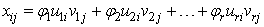
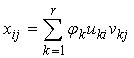
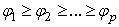 Equation (14) is known as the singular value decomposition (SVD) of matrix X. The number of terms in (15) is r which is the rank of matrix X; r cannot exceed n or p whichever is smaller.It is assumed that
Equation (14) is known as the singular value decomposition (SVD) of matrix X. The number of terms in (15) is r which is the rank of matrix X; r cannot exceed n or p whichever is smaller.It is assumed that 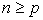 , and it follows that
, and it follows that 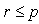 . The r vectors u are orthogonal to each other, as are the r vectors v. Furthermore, each of these vectors has unit length so that;
. The r vectors u are orthogonal to each other, as are the r vectors v. Furthermore, each of these vectors has unit length so that;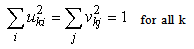
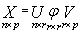
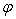 is diagonal, and all
is diagonal, and all 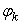 are positive. The columns of the matrix U are the u vectors, and the rows of V’ are the v vectors of (12). The orthogonality of the u and v and their unit length implies the conditions
are positive. The columns of the matrix U are the u vectors, and the rows of V’ are the v vectors of (12). The orthogonality of the u and v and their unit length implies the conditions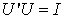
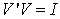
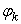 can be shown to be the square roots of the non zero eigenvalues of the square matrix
can be shown to be the square roots of the non zero eigenvalues of the square matrix 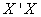 as well as the square matrix
as well as the square matrix 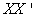 . The columns of U are the eigenvectors of
. The columns of U are the eigenvectors of 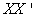 and the rows of V’ are the eigenvectors of
and the rows of V’ are the eigenvectors of 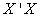 . When
. When 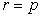 it is known as a full-rank case. Each element of X is easily reconstructed by multiplying the corresponding elements of the
it is known as a full-rank case. Each element of X is easily reconstructed by multiplying the corresponding elements of the 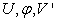 matrices and summing the terms.From equation (3)
matrices and summing the terms.From equation (3) 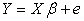 We obtain
We obtain 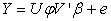
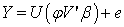 Where
Where 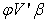 is a
is a 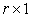 matrix, that is a vector of r elements. Let us denote the vector by
matrix, that is a vector of r elements. Let us denote the vector by 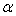 .
.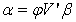
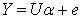
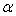 is obtained by the usual matrix equation
is obtained by the usual matrix equation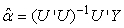 which, as a result of (17) becomes
which, as a result of (17) becomes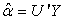
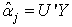 simply the inner product of the matrix Y with jth vector
simply the inner product of the matrix Y with jth vector 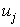 . It follows from (21) that
. It follows from (21) that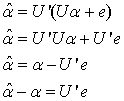 But E
But E 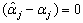
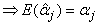
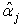 is unbiased. Furthermore, the variance of
is unbiased. Furthermore, the variance of 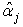 is
is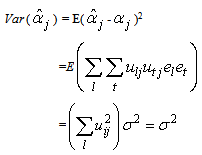 Hence
Hence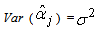
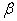 and
and 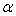 is given by equation (20), which also holds for the least squares estimates of
is given by equation (20), which also holds for the least squares estimates of 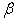 and
and 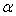
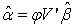
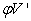 has the dimension
has the dimension 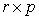 . Thus, given the
. Thus, given the 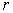 values of
values of 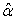 , the matrix relation (25) represents r equations in p unknown parameter estimates
, the matrix relation (25) represents r equations in p unknown parameter estimates 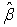 . If r=p (the full-rank case). The solution is possible and unique.In this case V’ is a
. If r=p (the full-rank case). The solution is possible and unique.In this case V’ is a 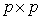 orthogonal matrix.Hence, the solution is given by
orthogonal matrix.Hence, the solution is given by 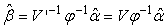
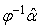 is
is 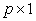 vector, obtained by dividing each
vector, obtained by dividing each 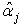 by the corresponding
by the corresponding 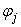 .An important use of (26) aside from its supplying the estimates of
.An important use of (26) aside from its supplying the estimates of 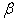 as functions of
as functions of 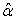 , is the ready calculation of the variances of the
, is the ready calculation of the variances of the 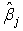 . In general notation this equation is written as
. In general notation this equation is written as 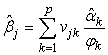
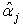 are mutually orthogonal and have all variances
are mutually orthogonal and have all variances 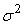 we see that
we see that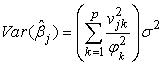
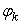 .
.
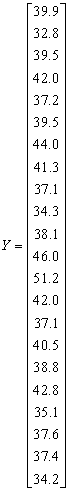 From equation (9) we obtain the cross-product of matrices
From equation (9) we obtain the cross-product of matrices 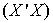 and
and 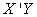 , Using MATLAB
, Using MATLAB 
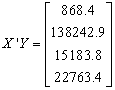 We then obtain
We then obtain 
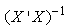 is the variance/co-variance matrix.
is the variance/co-variance matrix.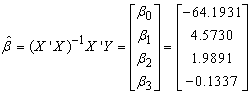
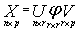 Matrix X as defined earlier;Using MATLAB we obtain the Matrices
Matrix X as defined earlier;Using MATLAB we obtain the Matrices 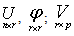 For U (see appendix)
For U (see appendix) Therefore, if
Therefore, if 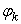 is the square roots of the non-zero eigen-values of the square matrix
is the square roots of the non-zero eigen-values of the square matrix 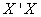 as well as the square matrix
as well as the square matrix 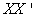 .The eigen-values of matrix
.The eigen-values of matrix  using MATLAB is obtained below
using MATLAB is obtained below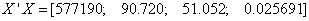 Redefining the Matrix
Redefining the Matrix 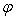 by leaving the non-zero vectors; we have
by leaving the non-zero vectors; we have Similarly, the columns U are the eigen-vectors of
Similarly, the columns U are the eigen-vectors of 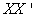 and the rows of V’ are the eigen-vectors of
and the rows of V’ are the eigen-vectors of 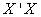 .To obtain the parameter estimates, from equation (26)
.To obtain the parameter estimates, from equation (26)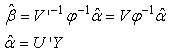 Where
Where 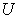 can be re-defined as column vectors U obtained from SVD (
can be re-defined as column vectors U obtained from SVD (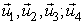 ) since r = 4, using MATLAB we have
) since r = 4, using MATLAB we have
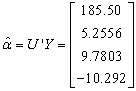 Similarly,
Similarly, 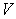 can be re-defined as row vectors V’ obtained from SVD (
can be re-defined as row vectors V’ obtained from SVD (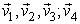 ) since r=4, using MATLAB we have
) since r=4, using MATLAB we have  Recall
Recall 

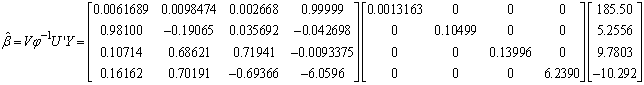
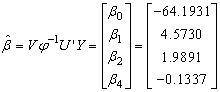 Similarly, obtaining the variances we have;
Similarly, obtaining the variances we have;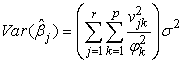 Using MATLAB
Using MATLAB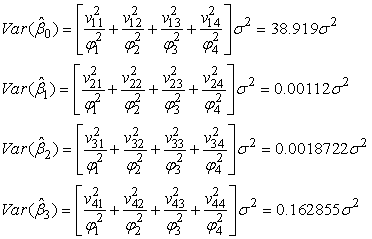 For obtaining co-variances we have;
For obtaining co-variances we have;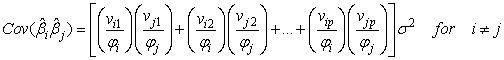 In general we have;
In general we have;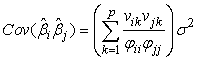
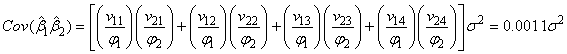
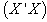 matrix is nonsingular (i.e
matrix is nonsingular (i.e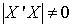 ). This is not often the case when predictor variables are linearly related, a situation often referred to as Perfect Collinearity or ill condition regression model.It then follows that, when
). This is not often the case when predictor variables are linearly related, a situation often referred to as Perfect Collinearity or ill condition regression model.It then follows that, when 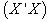 is singular, we can use SVD to approximate its inverse by the following matrix;
is singular, we can use SVD to approximate its inverse by the following matrix;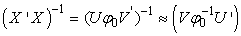
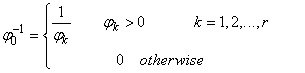 Equation (29) is a modified form of equation (16).
Equation (29) is a modified form of equation (16).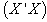 thus making it possible for users of the cross product matrix approach to obtain parameter estimates after obtaining the inverse of SVD of the matrix
thus making it possible for users of the cross product matrix approach to obtain parameter estimates after obtaining the inverse of SVD of the matrix 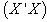 .
. 
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML