Oguntunde P. E. 1, Babatunde O. S. 2, Ogunmola A. O. 3
1Department of Mathematics, Covenant University, Ota, Ogun State, Nigeria
2Department of Mathematics, Statistics & Computer Science, Kwararafa University, Wukari, Taraba State, Nigeria
3Department of Mathematics & Statistics, Federal University, Wukari, Taraba State, Nigeria
Correspondence to: Oguntunde P. E. , Department of Mathematics, Covenant University, Ota, Ogun State, Nigeria.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The Kumaraswamy distribution being a viable alternative to the beta distribution is being used to propose a three-parameter Kumaraswamy-Inverse Exponential distribution and some of its statistical properties are identified.
Keywords:
Beta, Distribution, Inverse-Exponential, Kumaraswamy, Parameter
Cite this paper: Oguntunde P. E. , Babatunde O. S. , Ogunmola A. O. , Theoretical Analysis of the Kumaraswamy-Inverse Exponential Distribution, International Journal of Statistics and Applications, Vol. 4 No. 2, 2014, pp. 113-116. doi: 10.5923/j.statistics.20140402.05.
1. Introduction
The Inverted Exponential distribution was introduced by Keller and Kamath [5] and it has been studied and discussed in [7] as a lifetime model. If a random variable 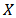 has an exponential distribution, the variable
has an exponential distribution, the variable 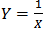 will have an inverted exponential (IE) distribution. Thus, a random variable X is said to have an Inverted Exponential distribution with parameter λ if its pdf and cdf are given respectively by;
will have an inverted exponential (IE) distribution. Thus, a random variable X is said to have an Inverted Exponential distribution with parameter λ if its pdf and cdf are given respectively by;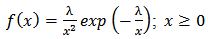 | (1) |
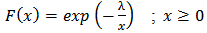 | (2) |
where 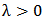 is the scale parameter.The development of a class of generalized distributions in [2] based on the logit of the beta random variable by using two parameters “a” and “b” whose role is to introduce skewness and vary the tail weight have led a number of authors to generalize several known theoretical distributions. The probability density function (pdf) of the beta-generalized distribution due to Eugene et al [2] is given by;
is the scale parameter.The development of a class of generalized distributions in [2] based on the logit of the beta random variable by using two parameters “a” and “b” whose role is to introduce skewness and vary the tail weight have led a number of authors to generalize several known theoretical distributions. The probability density function (pdf) of the beta-generalized distribution due to Eugene et al [2] is given by; 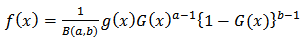 | (3) |
The corresponding cumulative density function (cdf) is given by;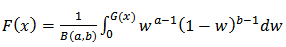 | (4) |
where 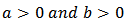
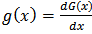 and
and 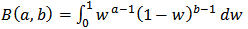 With this understanding, Eugene, et al [2] proposed and studied the Beta-Normal distribution. Other distributions such as Beta-Gumbel [9], Beta-Exponential [10], Beta-Inverse Weibull [3] and many others have also been defined and studied in literatures.According to Cordeiro and Castro [1], all these works lead to some mathematical difficulties because the beta distribution is not fairly tractable and, in particular, its cumulative distribution function (cdf) involves the incomplete beta function ratio. However, some researchers have suggested using alternative bounded distributions to generalize any parent distribution. Example of such alternative bounded distribution is the Kumaraswamy distribution.The Kumaraswamy distribution as defined by Ponndi Kumaraswamy (1980) in [6] has been identified as a viable alternative to Beta distribution because they both have the same basic shape properties (unimodal, uniantimodal, increasing, decreaing, monotone or constant) [4]. The pdf of the Kumaraswamy distribution is given by;
With this understanding, Eugene, et al [2] proposed and studied the Beta-Normal distribution. Other distributions such as Beta-Gumbel [9], Beta-Exponential [10], Beta-Inverse Weibull [3] and many others have also been defined and studied in literatures.According to Cordeiro and Castro [1], all these works lead to some mathematical difficulties because the beta distribution is not fairly tractable and, in particular, its cumulative distribution function (cdf) involves the incomplete beta function ratio. However, some researchers have suggested using alternative bounded distributions to generalize any parent distribution. Example of such alternative bounded distribution is the Kumaraswamy distribution.The Kumaraswamy distribution as defined by Ponndi Kumaraswamy (1980) in [6] has been identified as a viable alternative to Beta distribution because they both have the same basic shape properties (unimodal, uniantimodal, increasing, decreaing, monotone or constant) [4]. The pdf of the Kumaraswamy distribution is given by;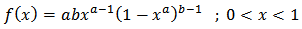 | (5) |
The corresponding cumulative density function (cdf) has a closed form given by;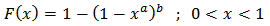 | (6) |
where 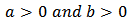 are shape parameters.The pdf given in equation (5) does not involve any incomplete beta function ratio and it is regarded as being tractable because of its mild algebraic properties [4].Cordeiro and Castro [1] combined the works of Eugene et al [2] and Jones [4] to construct a new family of generalized distributions based on the Kumaraswamy distribution. Starting from an arbitrary parent continuous cdf; G(x), the pdf and the cumulative density function F(x) of a Kumaraswamy-Generalized distribution is given respectively by;
are shape parameters.The pdf given in equation (5) does not involve any incomplete beta function ratio and it is regarded as being tractable because of its mild algebraic properties [4].Cordeiro and Castro [1] combined the works of Eugene et al [2] and Jones [4] to construct a new family of generalized distributions based on the Kumaraswamy distribution. Starting from an arbitrary parent continuous cdf; G(x), the pdf and the cumulative density function F(x) of a Kumaraswamy-Generalized distribution is given respectively by;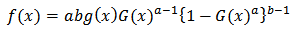 | (6) |
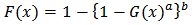 | (7) |
where 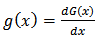 and parameters
and parameters 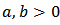 are additional shape parameters.According to [1], the distribution given by Equation (6) has an advantage over the class of generalized beta distributions due to [2], since it does not involve any special function.With this understanding, various distributions based on Kumaraswamy distribution can be defined. Recently developed is the Kumaraswamy-Inverse Weibull distribution [14].This paper seeks to introduce a three parameter Kumaraswamy-Inverse Exponential distribution and investigate some of its statistical properties.
are additional shape parameters.According to [1], the distribution given by Equation (6) has an advantage over the class of generalized beta distributions due to [2], since it does not involve any special function.With this understanding, various distributions based on Kumaraswamy distribution can be defined. Recently developed is the Kumaraswamy-Inverse Weibull distribution [14].This paper seeks to introduce a three parameter Kumaraswamy-Inverse Exponential distribution and investigate some of its statistical properties.
2. The Kumaraswamy-Inverse Exponential Distribution
The Kumaraswamy-Inverse Exponential distribution which we shall henceforth denote as K-IE distribution is derived by inserting Equations (1) and (2) in Equation (6). Hence, the probability density function (pdf) of a K-IE distribution with parameters 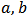 and
and 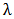 is given by;
is given by;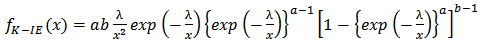 | (8) |
Where 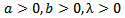 Alternatively, this can be re-written as;
Alternatively, this can be re-written as;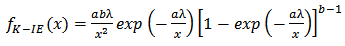 | (9) |
For notational purpose, we write;  It can be seen that if
It can be seen that if  , the distribution in Equation (9) reduces to an Inverse-Exponential Distribution with parameter
, the distribution in Equation (9) reduces to an Inverse-Exponential Distribution with parameter 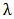 .Following the works of Hanook et al [3] and Shahbaz et al [14], Equation (9) can also be written in another form by using series representation given by Prudnikov et al [13] as;
.Following the works of Hanook et al [3] and Shahbaz et al [14], Equation (9) can also be written in another form by using series representation given by Prudnikov et al [13] as;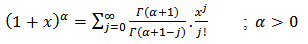 Thus, the probability density function (pdf) of the K-IE distribution can be re-written as;
Thus, the probability density function (pdf) of the K-IE distribution can be re-written as;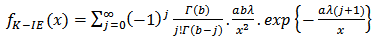 | (10) |
The corresponding cumulative density function (cdf) is given by;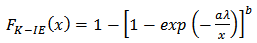 | (11) |
2.1. Asymptotic Behavior of the K-IE Distribution
We seek to investigate the behavior of the model in Equation (9) as 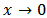 and as
and as 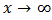 . This involves considering
. This involves considering 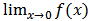 and
and 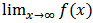 .As
.As 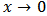 ;
;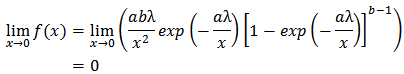 As
As 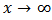 ;
;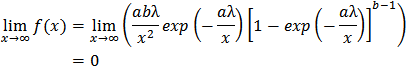 It can be deduced here that;
It can be deduced here that; 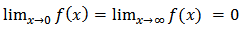 . These results show that the K-IE has only one mode.
. These results show that the K-IE has only one mode.
2.2. Shape of the K-IE Distribution
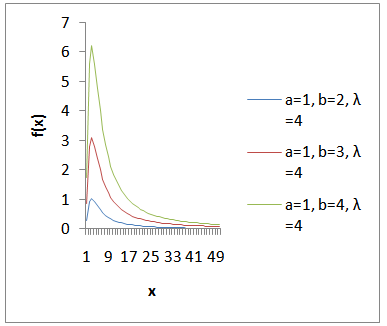
In this section, the shape of the K-IE distribution is revealed with the aid of graphs. The graphs of the pdf at various choices of parameters are given below as Figure 1 to Figure 4;Figure 1 shows that the K-IE distribution is positively skewed. Moreover, the lower the value of parameter ‘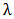 ’, the more skewed the curve becomes and the more the more the value of ‘
’, the more skewed the curve becomes and the more the more the value of ‘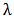 ’, the less skewed the curve becomes.
’, the less skewed the curve becomes.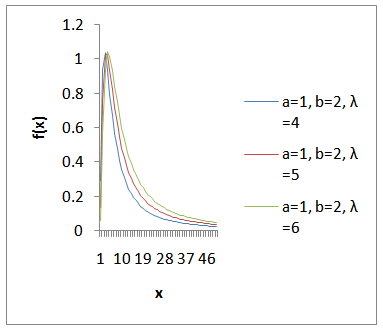 | Figure 1. The graph of the pdf of K-IE distribution at varying values of 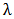 and constant values of “a” and ‘b” and constant values of “a” and ‘b” |
 | Figure 2. The graph of the pdf of K-IE distribution at varying values of “b” but constant values of “a” and “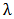 ” ” |
Figure 2 reveals that the peak of the distribution is based on parameter “b” as increase in the value of “b” increases the peak of the curve and decrease in the value of parameter ‘b’ results in decrease in the peak of the curve. In other words, parameter “b” controls the kurtosis of the model.Figure 3 shows that, the more the value of parameter ‘a’, the more spread out the curve becomes and the lower the value of parameter ‘a’, the more compacted the curve becomes. 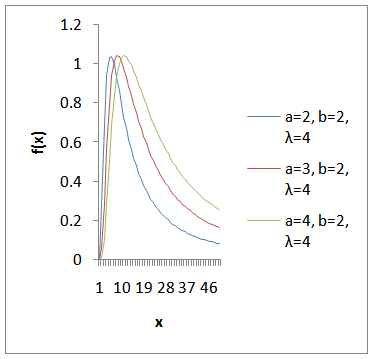 | Figure 3. The graph of the pdf of K-IE distribution at varying values of “a” but constant values of “b” and “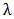 ” ” |
2.3. Properties of the K-IE Distribution
The r-th moment of the proposed K-IE distribution is presented below and the results (if the r-th moments exist) shall be used to compute the mean, variance, skewness and kurtosis of the K-IE distribution;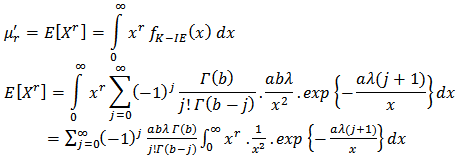 Let
Let 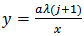 and simplifying further,
and simplifying further,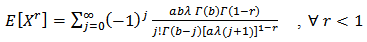 | (12) |
This is an indication that the r-th moment for the K-IE does not exist since the expression in Equation (12) only exist for 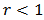 .
.
2.4. Survival and Hazard Function
The survival function for the Kumaraswamy-Inverse Exponential distribution is given by;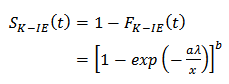 The hazard function is thus given by;
The hazard function is thus given by;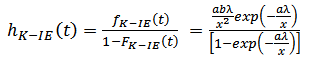 | (13) |
Choosing different values for the parameters 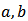 and
and 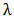 , the graph for the hazard function of the K-IE distribution is presented below;
, the graph for the hazard function of the K-IE distribution is presented below;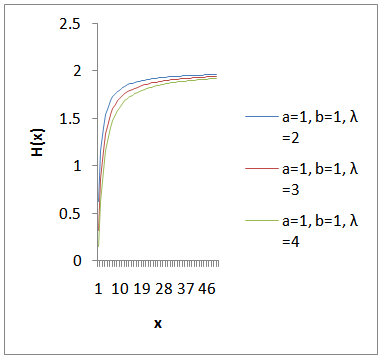 | Figure 4. The graph for the Hazard function of K-IE distribution for fixed “a” and ‘b” and varying values of “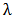 ” ” |
2.5. Parameter Estimation
In a view to estimating the parameters of the K-IE distribution, we employ the method of the Maximum Likelihood Estimation. Let 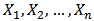 be a random sample of ‘n’ independently and identically distributed random variables each having a K-IE distribution defined in Equation (9), the likelihood function L is given by;
be a random sample of ‘n’ independently and identically distributed random variables each having a K-IE distribution defined in Equation (9), the likelihood function L is given by;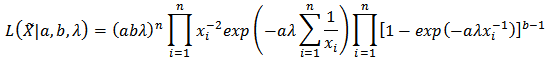 Let
Let 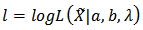
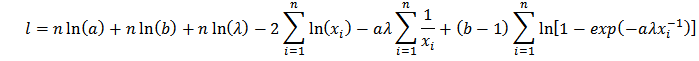 Differentiating
Differentiating 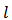 with respect to
with respect to 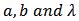 gives;
gives;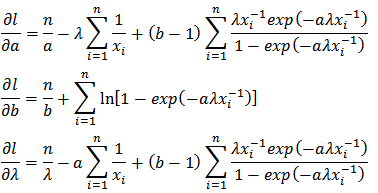 Solving
Solving 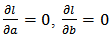 and
and 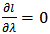 simultaneously gives the maximum likelihood estimates of
simultaneously gives the maximum likelihood estimates of 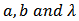 The observed information matrix for the parameters of K-IE is given below as;
The observed information matrix for the parameters of K-IE is given below as;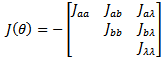 The entries in the matrix are given below as;
The entries in the matrix are given below as;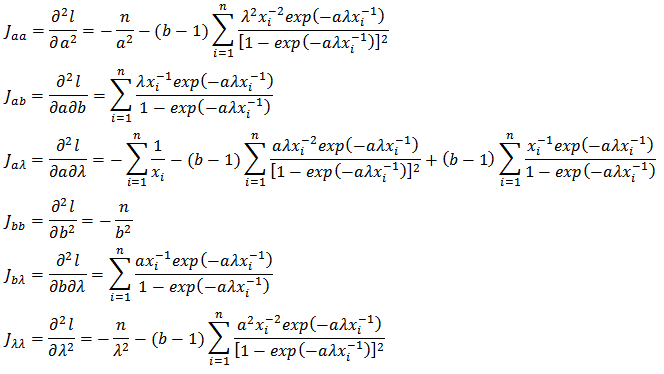
3. Conclusions
In this article, a three-parameter distribution called the Kumaraswamy Inverse Exponential distribution (denoted by K-IE distribution) is being introduced. Its parameters were estimated and an explicit expression for the r-th moment is given. The distribution is leptokurtic. A one-parameter Inverse Exponential distribution is being identified as a special case of the new distribution. It is expected that the K-IE distribution would have an advantage over the Beta Inverse Exponential distribution in terms of tractability because the former does not involve any special function like the incomplete beta function ratio. Since g(.) and G(.) in Equation (6) are tractable, the K-IE distribution can be used effectively even if the data are censored. It is also expected that the K-IE distribution will receive appreciable usage in hydrology and would be useful as a basis for further researches in distribution theory.
References
| [1] | Cordeiro, G. M and Castro, M de (2010). “A new family of generalized distributions”. Journal of Statistical Computation and Simulation. DOI: 10.1080/0094965YY. |
| [2] | Eugene, N., Lee, C., Famoye, F (2002). “Beta-Normal distribution and its applications”. Communication in Statistics: Theory and Methods, Vol. 31, 497-512. |
| [3] | Hanook, S., Shahbaz, M.Q, Moshin, M and Kibra, G (2013). “A note on Beta Inverse Weibull distribution”. Communication in Statistics: Theory and Methods, 42:2, 320-335. |
| [4] | Jones, M. C (2009). Kumaraswamy’s distribution: “A beta-type distribution with some tractability advantages”. Statistical Methodology. 6, 70-81. |
| [5] | Keller, A. Z and Kamath, A. R (1982). “Reliability analysis of CNC Machine Tools”. Reliability Engineering. Vol. 3, pp. 449-473. |
| [6] | Kumaraswamy, P (1980). “A generalized probability density function for double-bounded random processes”. Journal of Hydrology, Vol. 46, 79-88. |
| [7] | Lin, C. T, Duran, B. S and Lewis, T. O (1989). “Inverted Gamma as life distribution”. Microelectron Reliability, Vol. 29 (4), 619-626. |
| [8] | Nadarajah, S. (2008). “On the distribution of Kumaraswamy”. Journal of Hydrology. 348 (2008) 568-569. |
| [9] | Nadarajah, S. and Kotz, S. (2004). “The Beta-Gumbel Distribution”. Mathematical Problems in Engineering, 10, 323-332. |
| [10] | Nadarajah, S., Kotz, S. (2006). “The Beta-Exponential Distribution”. Reliability Engineering and System Safety. 91, 689-697. |
| [11] | Nadarajah, S. and Eljabri, S. (2013). “The Kumaraswamy GP Distribution”. Journal of Data Science, 11 (2013), 739-766. |
| [12] | Oguntunde, P. E, Odetunmibi, O.A, Adejumo A.O (2014). “On the Sum of exponentially distributed random variables: A convolution approach”. European Journal of Statistics and Probability, 2(1), 1-8 |
| [13] | Prudnikov, A. P., Brychkov, Y. A and Marichev, O. I (1986). “Integrals and Series.Vol. 3, Gordon and Breach Science Publishers, New York. |
| [14] | Shahbaz, M.Q, Shahbaz, S, Butt N. S (2012). “The Kumaraswamy-Inverse Weibull Distribution”. Pakistan Journal of Statistics and Operation Research, Vol 8, No. 3, 479-489. |

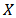 has an exponential distribution, the variable
has an exponential distribution, the variable 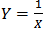 will have an inverted exponential (IE) distribution. Thus, a random variable X is said to have an Inverted Exponential distribution with parameter λ if its pdf and cdf are given respectively by;
will have an inverted exponential (IE) distribution. Thus, a random variable X is said to have an Inverted Exponential distribution with parameter λ if its pdf and cdf are given respectively by;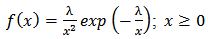
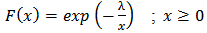
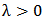 is the scale parameter.The development of a class of generalized distributions in [2] based on the logit of the beta random variable by using two parameters “a” and “b” whose role is to introduce skewness and vary the tail weight have led a number of authors to generalize several known theoretical distributions. The probability density function (pdf) of the beta-generalized distribution due to Eugene et al [2] is given by;
is the scale parameter.The development of a class of generalized distributions in [2] based on the logit of the beta random variable by using two parameters “a” and “b” whose role is to introduce skewness and vary the tail weight have led a number of authors to generalize several known theoretical distributions. The probability density function (pdf) of the beta-generalized distribution due to Eugene et al [2] is given by; 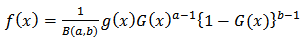
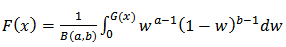
 and
and 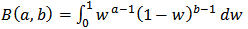 With this understanding, Eugene, et al [2] proposed and studied the Beta-Normal distribution. Other distributions such as Beta-Gumbel [9], Beta-Exponential [10], Beta-Inverse Weibull [3] and many others have also been defined and studied in literatures.According to Cordeiro and Castro [1], all these works lead to some mathematical difficulties because the beta distribution is not fairly tractable and, in particular, its cumulative distribution function (cdf) involves the incomplete beta function ratio. However, some researchers have suggested using alternative bounded distributions to generalize any parent distribution. Example of such alternative bounded distribution is the Kumaraswamy distribution.The Kumaraswamy distribution as defined by Ponndi Kumaraswamy (1980) in [6] has been identified as a viable alternative to Beta distribution because they both have the same basic shape properties (unimodal, uniantimodal, increasing, decreaing, monotone or constant) [4]. The pdf of the Kumaraswamy distribution is given by;
With this understanding, Eugene, et al [2] proposed and studied the Beta-Normal distribution. Other distributions such as Beta-Gumbel [9], Beta-Exponential [10], Beta-Inverse Weibull [3] and many others have also been defined and studied in literatures.According to Cordeiro and Castro [1], all these works lead to some mathematical difficulties because the beta distribution is not fairly tractable and, in particular, its cumulative distribution function (cdf) involves the incomplete beta function ratio. However, some researchers have suggested using alternative bounded distributions to generalize any parent distribution. Example of such alternative bounded distribution is the Kumaraswamy distribution.The Kumaraswamy distribution as defined by Ponndi Kumaraswamy (1980) in [6] has been identified as a viable alternative to Beta distribution because they both have the same basic shape properties (unimodal, uniantimodal, increasing, decreaing, monotone or constant) [4]. The pdf of the Kumaraswamy distribution is given by;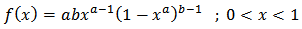
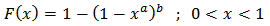
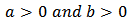 are shape parameters.The pdf given in equation (5) does not involve any incomplete beta function ratio and it is regarded as being tractable because of its mild algebraic properties [4].Cordeiro and Castro [1] combined the works of Eugene et al [2] and Jones [4] to construct a new family of generalized distributions based on the Kumaraswamy distribution. Starting from an arbitrary parent continuous cdf; G(x), the pdf and the cumulative density function F(x) of a Kumaraswamy-Generalized distribution is given respectively by;
are shape parameters.The pdf given in equation (5) does not involve any incomplete beta function ratio and it is regarded as being tractable because of its mild algebraic properties [4].Cordeiro and Castro [1] combined the works of Eugene et al [2] and Jones [4] to construct a new family of generalized distributions based on the Kumaraswamy distribution. Starting from an arbitrary parent continuous cdf; G(x), the pdf and the cumulative density function F(x) of a Kumaraswamy-Generalized distribution is given respectively by;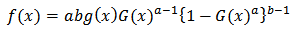
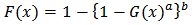
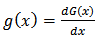 and parameters
and parameters 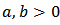 are additional shape parameters.According to [1], the distribution given by Equation (6) has an advantage over the class of generalized beta distributions due to [2], since it does not involve any special function.With this understanding, various distributions based on Kumaraswamy distribution can be defined. Recently developed is the Kumaraswamy-Inverse Weibull distribution [14].This paper seeks to introduce a three parameter Kumaraswamy-Inverse Exponential distribution and investigate some of its statistical properties.
are additional shape parameters.According to [1], the distribution given by Equation (6) has an advantage over the class of generalized beta distributions due to [2], since it does not involve any special function.With this understanding, various distributions based on Kumaraswamy distribution can be defined. Recently developed is the Kumaraswamy-Inverse Weibull distribution [14].This paper seeks to introduce a three parameter Kumaraswamy-Inverse Exponential distribution and investigate some of its statistical properties.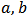 and
and 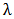 is given by;
is given by;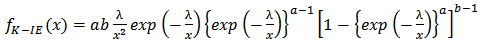
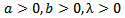 Alternatively, this can be re-written as;
Alternatively, this can be re-written as;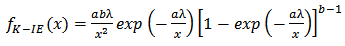
 It can be seen that if
It can be seen that if  , the distribution in Equation (9) reduces to an Inverse-Exponential Distribution with parameter
, the distribution in Equation (9) reduces to an Inverse-Exponential Distribution with parameter  .Following the works of Hanook et al [3] and Shahbaz et al [14], Equation (9) can also be written in another form by using series representation given by Prudnikov et al [13] as;
.Following the works of Hanook et al [3] and Shahbaz et al [14], Equation (9) can also be written in another form by using series representation given by Prudnikov et al [13] as;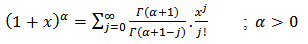 Thus, the probability density function (pdf) of the K-IE distribution can be re-written as;
Thus, the probability density function (pdf) of the K-IE distribution can be re-written as;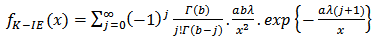
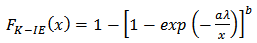
 and as
and as 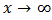 . This involves considering
. This involves considering 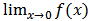 and
and 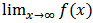 .As
.As 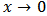 ;
;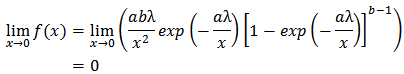 As
As 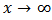 ;
;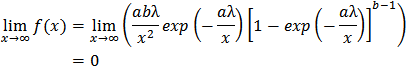 It can be deduced here that;
It can be deduced here that; 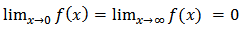 . These results show that the K-IE has only one mode.
. These results show that the K-IE has only one mode.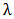 ’, the more skewed the curve becomes and the more the more the value of ‘
’, the more skewed the curve becomes and the more the more the value of ‘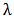 ’, the less skewed the curve becomes.
’, the less skewed the curve becomes.
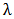 and constant values of “a” and ‘b”
and constant values of “a” and ‘b”
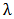 ”
”
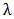 ”
”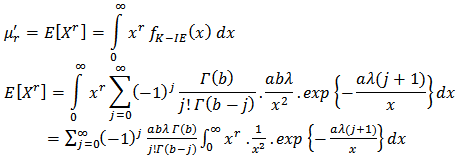 Let
Let 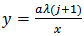 and simplifying further,
and simplifying further,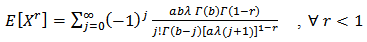
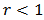 .
.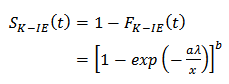 The hazard function is thus given by;
The hazard function is thus given by;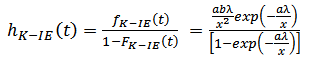
 and
and 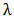 , the graph for the hazard function of the K-IE distribution is presented below;
, the graph for the hazard function of the K-IE distribution is presented below;
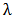 ”
”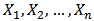 be a random sample of ‘n’ independently and identically distributed random variables each having a K-IE distribution defined in Equation (9), the likelihood function L is given by;
be a random sample of ‘n’ independently and identically distributed random variables each having a K-IE distribution defined in Equation (9), the likelihood function L is given by;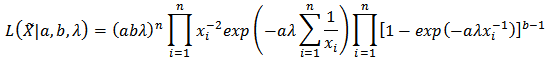 Let
Let 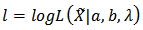
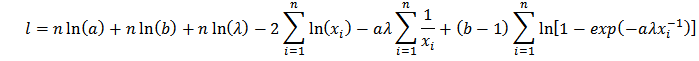 Differentiating
Differentiating 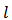 with respect to
with respect to 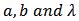 gives;
gives;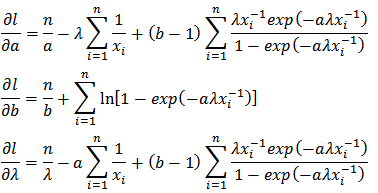 Solving
Solving 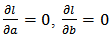 and
and 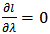 simultaneously gives the maximum likelihood estimates of
simultaneously gives the maximum likelihood estimates of 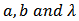 The observed information matrix for the parameters of K-IE is given below as;
The observed information matrix for the parameters of K-IE is given below as;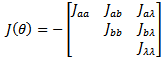 The entries in the matrix are given below as;
The entries in the matrix are given below as;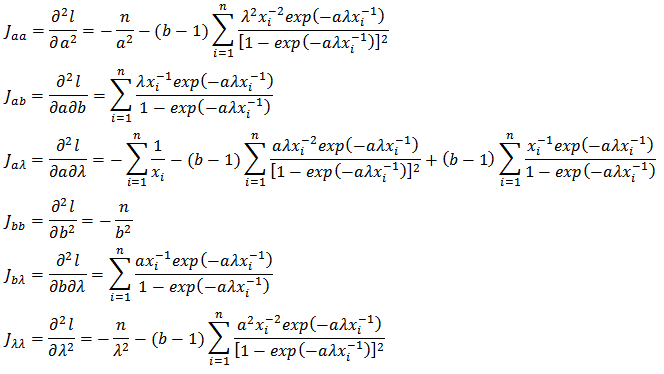
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML