Hamdy M. Salem1, Mahmoud Ali Selim2
1Department of Statistics, Faculty of Commerce, Al-Azher University, Egypt & Qassim University, Community College in Buraidah, Saudi Arabia
2Department of Statistics, Faculty of Commerce, Al-Azher University, Egypt
Correspondence to: Hamdy M. Salem, Department of Statistics, Faculty of Commerce, Al-Azher University, Egypt & Qassim University, Community College in Buraidah, Saudi Arabia.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This paper defines a new distribution, namely, Generalized Weibull- Exponential distribution GWED. This distribution extends a Weibull-Exponential distribution which is generated from family of generalized T-X distributions. Different properties for the GWED are obtained such as moments, limiting behavior, quantile function, Shannon’s entropy, skewness and kurtosis. Finally, analysis of several real data sets are carried out and thereafter compared the results with other distributions to illustrate the applications of the GWED.
Keywords:
Exponentiated Distribution, T-X Distribution, Shannon’s Entropy, Limiting Behavior, Hazard Function
Cite this paper: Hamdy M. Salem, Mahmoud Ali Selim, The Generalized Weibull-Exponential Distribution: Properties and Applications, International Journal of Statistics and Applications, Vol. 4 No. 2, 2014, pp. 102-112. doi: 10.5923/j.statistics.20140402.04.
1. Introduction
Although the statistical distributions used to describe and interpret the phenomena, there are continuous motivations for developing these distributions to become more flexible or more fitting for specific real data sets. These new statistical distributions are called exponentiated distributions. The idea of exponentiated distributions were utilized to create new distributions. Cordeiro & Castro (2011) [5] extended many known distributions as normal, Weibull, gamma, Gumbel, and inverse Gaussian distributions. They expressed the ordinary moments of these new family of generalized distributions as linear functions of probability weighted moments of the parent distribution. Mudholkar & Srivastava (1994) [11] proposed the exponentiated Weibull distribution to analyze bathtub failure data. Gupta et al (1998) [8] introduced a class of exponentiated distributions which is based on cumulative distribution function as follows: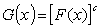 | (1.1) |
where 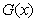 is the cumulative distribution function of the random variable
is the cumulative distribution function of the random variable 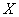 and c is an additional shape parameter.The Weibull and exponential distributions are the most widely used in the reliability and survival studies. This is due to their simplicity and easy mathematical manipulations. In additions, the exponential distribution is one of the members for Weibull-
and c is an additional shape parameter.The Weibull and exponential distributions are the most widely used in the reliability and survival studies. This is due to their simplicity and easy mathematical manipulations. In additions, the exponential distribution is one of the members for Weibull-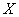 family as well. Let
family as well. Let 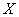 be a random variable taken from exponential distribution with probability density function pdf and cumulative distribution function (CDF) respectively,
be a random variable taken from exponential distribution with probability density function pdf and cumulative distribution function (CDF) respectively, 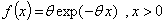 and
and 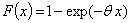 . Also, let
. Also, let 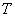 be a random variable taken from Weibull distribution with pdf is
be a random variable taken from Weibull distribution with pdf is 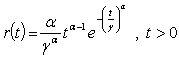 . Then, the pdf of Weibull-Exponential distribution is
. Then, the pdf of Weibull-Exponential distribution is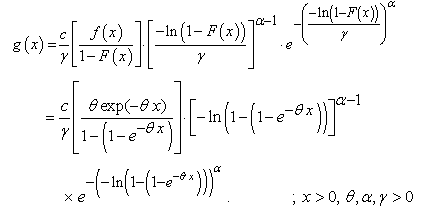 | (1.2) |
For the exponentiated T-X distribution, Alzaatreh et al (2013) [2] proposed a new method for generating many new distributions. It is called, the T -X family of distributions. It has a connection between the hazard functions and each generated distribution as a weighted hazard function of the random variable X. Alzaatreh et al (2013) [2] founded several known continuous distributions to be special cases of these new distributions. Akinsete et al (2008) [1] studied a four-parameter beta-Pareto distribution. They discussed various properties of the distribution and they founded the distribution to be unimodal and has either a unimodal or a decreasing hazard rate. Also, they obtained the mean, mean deviation, variance, skewness, kurtosis entropies, and they used the method of maximum likelihood to estimate the parameters. Carl et al (2013) [4] used five general methods of combination and variations of two historical periods. These combinations for generating statistical distribution approaches are the method of generating skew distributions, the method of adding parameters, beta generated method, transformed-transformer method and composite method.The paper is organized as follows. In Section 2, The GWED will be defined. The properties for the new distribution as moments, limiting behavior, quantile function, Shannon’s entropy, skewness and kurtosis are discussed in section 3. Finally, comparing of results for the GWED with other distributions via real data sets.
2. The GWED
Alzaghal A. et al (2013) [3] presented the pdf of the Exponentiated T-X distributions as follows 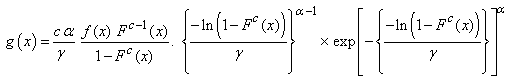 | (2.1) |
therefore, the pdf of the GWED is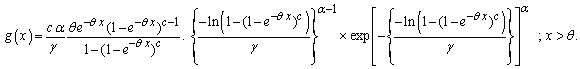 | (2.2) |
And the CDF is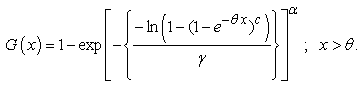 | (2.3) |
where 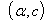 are the shape parameters and
are the shape parameters and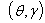 are the scale parameters respectively.In (2.3), note that, if
are the scale parameters respectively.In (2.3), note that, if 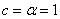 , the pdf of the GWED reduces to the exponential distribution with parameter
, the pdf of the GWED reduces to the exponential distribution with parameter 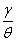 . Also, when
. Also, when 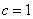 and the GWED reduces to the Weibull distribution with parameters
and the GWED reduces to the Weibull distribution with parameters 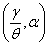 . The exponentiated exponential distribution produced when
. The exponentiated exponential distribution produced when 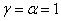 as well.
as well.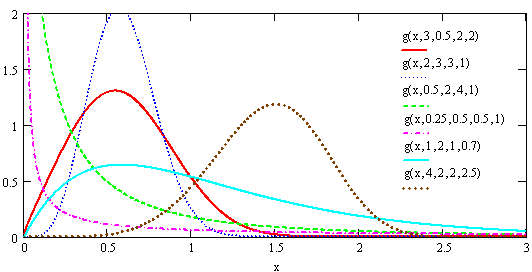 | Figure (1). Different forms for pdf of the GWED with various values of the parameters 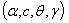 respectively respectively |
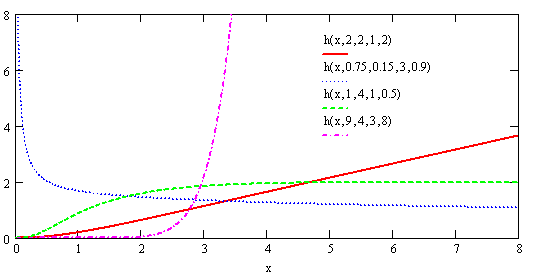 | Figure (2). Different forms for hazard function of the GWED with various values of the parameters 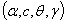 respectively respectively |
The survival function and the hazard function of the GWED respectively take the following forms: 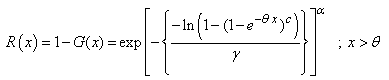 | (2.4) |
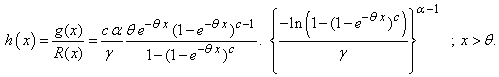 | (2.5) |
3. Properties of the GWED
There are some relations between the GWED and another distributions. These relations can be obtained by using the transform of variables. For example, let  be an Exponentiated Weibull random variable with parameters
be an Exponentiated Weibull random variable with parameters 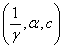 , then, using this transform
, then, using this transform 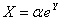 , the result is the pdf for the GWED. Also, if
, the result is the pdf for the GWED. Also, if 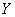 be a standard exponential random variable with parameters
be a standard exponential random variable with parameters 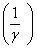 , then, using
, then, using 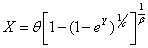 as a transform, the result is the pdf for the GWED. And using the transform
as a transform, the result is the pdf for the GWED. And using the transform 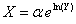 be a random variable for the Exponentiated Frechet distribution to get on the pdf of the GWED.
be a random variable for the Exponentiated Frechet distribution to get on the pdf of the GWED.
3.1. Limiting Behaviors of PDF and Hazard Function
The limiting behaviors of the pdf for the GWED is given by the following lemmas.Lemma 1: The limit of GWED density is zero when 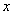 goes to infinity, and when
goes to infinity, and when 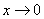 , the limit is given by:
, the limit is given by: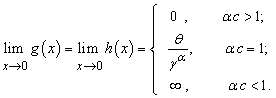 | (3.1.1) |
Proof. A result in (3.1.1) can be proofed as follows :  | (3.1.2) |
When 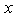 goes to zero, the limit of the quantity between brackets
goes to zero, the limit of the quantity between brackets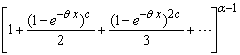 equals one. So, (3.1.2) reduces to:
equals one. So, (3.1.2) reduces to: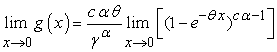 | (3.1.3) |
If 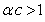 , then, (3.1.3) goes to zero, if
, then, (3.1.3) goes to zero, if 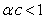 , it goes to infinity and if
, it goes to infinity and if 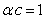 , it reduces to
, it reduces to 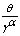 .Lemma 2: The limiting of the hazard function for the GWED when
.Lemma 2: The limiting of the hazard function for the GWED when 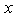 goes to infinity is:
goes to infinity is: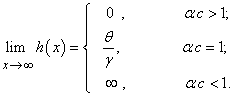 | (3.1.4) |
Proof. The result comes by using a similar proof as in lemma 1.
3.2. Quantile Function and Shannon Entropy
Alzaghal et al (2013) [3] concluded the quantile function 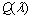 and Shannon entropy
and Shannon entropy 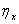 for the Exponentiated T-X distributions by using the CDF for the X and T distributions as follows:
for the Exponentiated T-X distributions by using the CDF for the X and T distributions as follows: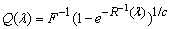 | (3.2.1) |
And 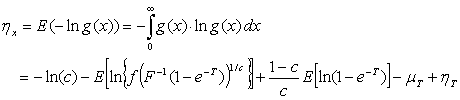 | (3.2.2) |
So, the 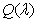 and
and 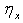 of the GWED respectively are:
of the GWED respectively are: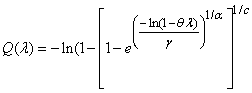 | (3.2.3) |
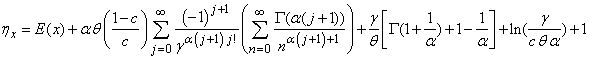 | (3.2.4) |
And the quartiles of the GWED can be obtained by setting 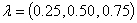 in (3.2.3). Also, based on quartiles, the skewness and kurtosis for the GWED respectively are:
in (3.2.3). Also, based on quartiles, the skewness and kurtosis for the GWED respectively are: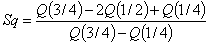 | (3.2.3) |
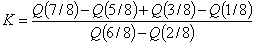 | (3.2.4) |
3.3. Moments
The 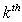 moments of the GWED can be obtained via the moment generating function which can be derived as follows:
moments of the GWED can be obtained via the moment generating function which can be derived as follows: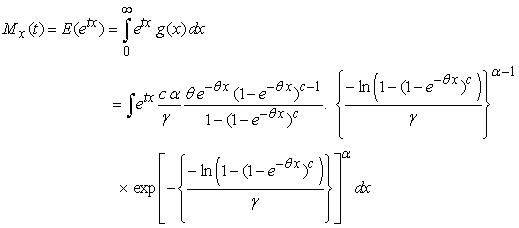 | (3.3.1) |
Let 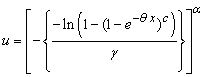 , then,
, then, 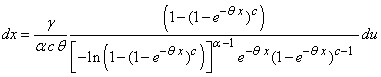 , and the integral in (3.3.1) can be written as:
, and the integral in (3.3.1) can be written as: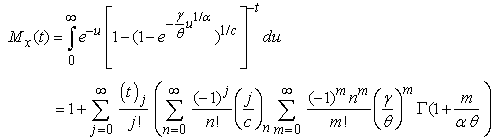 | (3.3.2) |
where 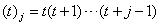 .The result in (3.3.3) came by using the following series expansions:
.The result in (3.3.3) came by using the following series expansions: 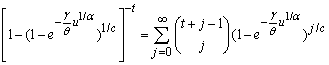 ,
,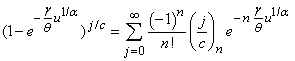 and
and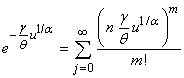 .
.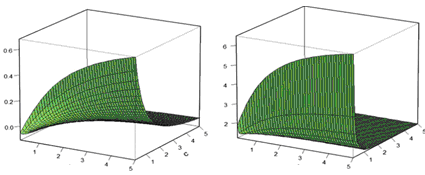 | Figure (3). Skewness and Kurtosis of the GWED |
Now, taking the 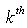 derivative of (3.3.2) and replacing
derivative of (3.3.2) and replacing 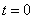 to obtain the
to obtain the 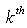 moments. Therefore,
moments. Therefore, 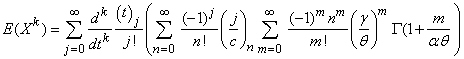 | (3.3.3) |
The mean of the GWED is: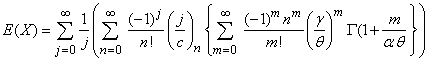 | (3.3.4) |
And the variance of the GWED is: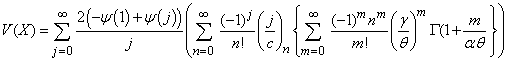 | (3.3.5) |
Table (1) shows that the mean and variance of GWED are increasing when 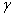 and c increase. And
and c increase. And 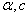 are fixed the mean of GWED is increase while the mean and variance of GWED are decrease.
are fixed the mean of GWED is increase while the mean and variance of GWED are decrease.Table (1). Mean and variance for the GWED various values
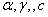 and and
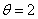 is fixed is fixed
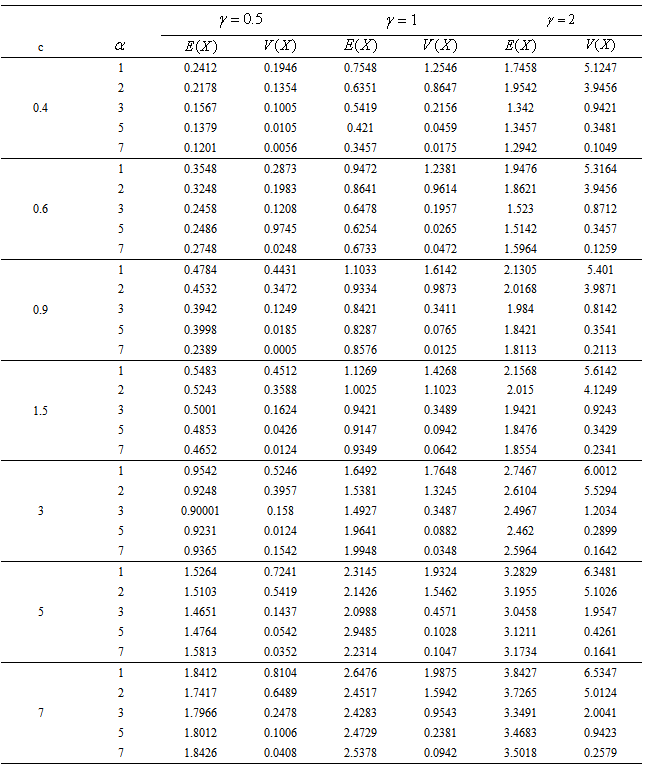 |
| |
|
4. Application
Park et al (1964) [14] and Park (1954) [13] presented three frequency distributions related to adult numbers of Tribolium Confusum, Tribolium Castaneum Cultured at 24℃ and Tribolium Confusum strain. These data sets can be fitted via different distributions. For example, Exponentiated Weibull, Generalized Weibull, Lagrange-Gamma and Weibull-Exponential distributions which were presented by Mudholkar et al (1995) [11], Mudholkar et al (1996) [12], Famoya & Govindarajulu (1998) [6] and Alzaatreh et al (2013) [2] respectively. The main objective of this application is to compare the previously mentioned distributions with the GWED to provide an adequate distribution that best fits data. Tables (2), (3) and (4) show relatively better fit of data for the GWED than for the other four distributions and corresponding p-value and skewness are the highest for the GWED among all the distribution considered.Table (2). Calculated
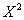 Values for Tribolium Castaneum Cultured at Values for Tribolium Castaneum Cultured at
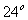 C C
 |
| |
|
Table (3). Calculated
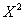 Values for Tribolium Castaneum Cultured at 24℃ Values for Tribolium Castaneum Cultured at 24℃
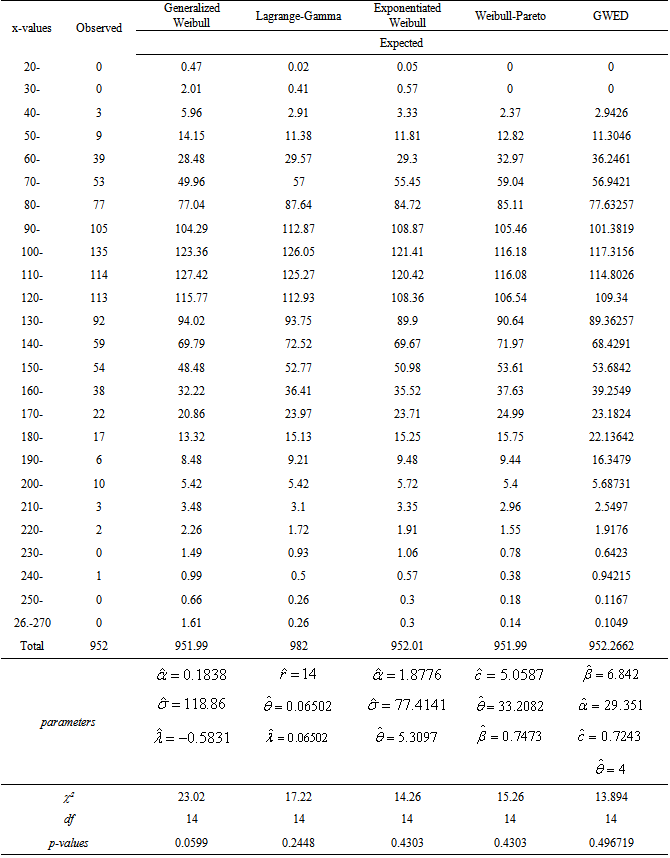 |
| |
|
Table (4). Calculated
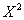 Values for Tribolium Castaneum Cultured at 24℃ Values for Tribolium Castaneum Cultured at 24℃
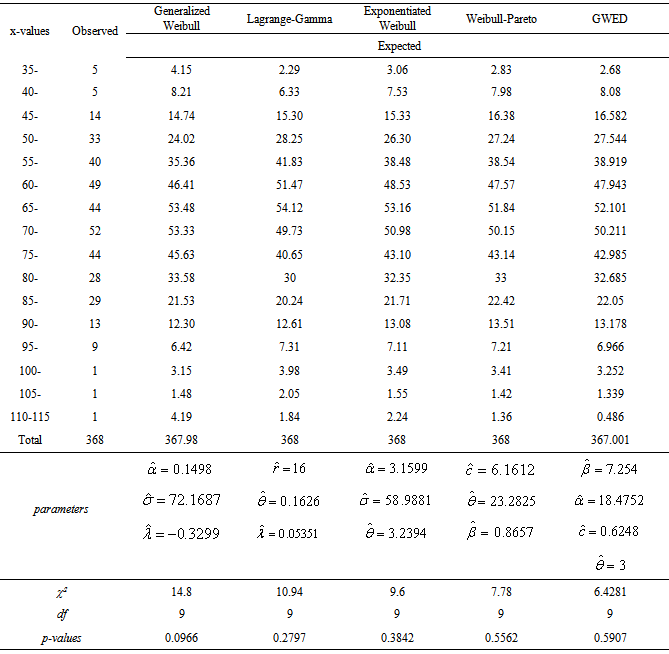 |
| |
|
5. Conclusions
In this paper, The Generalized Weibull-Exponential Distribution has been defined and studied. various properties of GWED including moments, variance, quantal function, Shannon entropy, skewness and kurtosis have been obtained. Three real data were fitted for the GWED and compared with four known distributions. The results showed that the GWED is a relatively better model to fit data than the other four distributions and the GWED characterized with highest p-value and skewness among the other.In simulation study, the mean and variance of GWED are increasing when the parameters 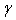 and c increase. And
and c increase. And 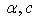 are fixed the mean of GWED is increase while the mean and variance of GWED are decrease.
are fixed the mean of GWED is increase while the mean and variance of GWED are decrease.
References
| [1] | Akinsete A., Famoye F., & Lee C. (2008). "The beta-Pareto distribution". Statistics. 42. 547-563. |
| [2] | Alzaatreh A., Carl Lee & Felix F. (2013). "A new method for generating families of continuous distributions". METRON. 71. 63–79. |
| [3] | Alzaghal A., Felix F. & Carl L. (2013). "Exponentiated T-X Family of Distributions with Some Applications". International Journal of Statistics and Probability. 2(3). 31-49. |
| [4] | Carl L., Felix F., & Alzaatreh A, (2013). "Methods for generating families of univariate continuous distributions in the recent decades". Computational Statistics. 5. 219–238. |
| [5] | Cordeiro M. & Castro M. (2011). "A new family of generalized distributions". Journal of Statistical Computation and Simulation. 81(7). 883-898.http://dx.doi.org/10.1080/00949650903530745. |
| [6] | Famoye F.& Govindarajulu Z. (1998). "On the Lagrange gamma distribution". Computat. Statist. Data Anal. 27. 421–431. |
| [7] | Famoye F., Lee C.& Olumolade, O. (2005). "The beta-weibull distribution". J. Statist. Theor. Appl. 4(2). 121–136. |
| [8] | Gupta C., Gupta P., & Gupta D. (1998). "Modeling failure time data by Lehmann alternatives". Communications in Statistics-Theory and Methods 27. 887-904.http://dx.doi.org/10.1080/03610929808832134. |
| [9] | Kececioglu D. (1991)." Reliability Engineering Handbook". Prentice Hall, Inc., Englewood Cliffs, New Jersey. |
| [10] | Mudholkar S. & Kollia D. (1994). "Generalized Weibull family: A structural analysis". Commun. Statist. Theor. Meth. 23(4). 1149–1171. |
| [11] | Mudholkar S., Srivastava K.& Freimer M. (1995). "The exponentiated Weibull family: a reanalysis of the bus-motor-failure data". Technometrics 37(4). 436–445. |
| [12] | Mudholkar S., Srivastava, D. & Kollia, G. (1996). "A generalization of the Weibull distribution with application to the analysis of survival data". J. Amer. Statist. Assoc. 91(436). 1575–1583. |
| [13] | Park T. (1954). "Experimental studies of interspecies competition II. Temperature, humidity, and competition in two species of Tribolium". Physiolog. Zool. 27. 177–238. |
| [14] | Park T., Leslie P. & Mertz, D. (1964). "Genetic strains and competition in population of Tribolium". Physiolog. Zool. 37. 97–162. |
| [15] | Sayama S. & Sekine M. (2004). "Suppression of sea-ice clutter observed by a millimeter wave radar using a new log-Weibull/CFAR system". Int. J. Infrared Millimeter Waves 25. 1481–1494. |
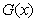 is the cumulative distribution function of the random variable
is the cumulative distribution function of the random variable 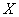 and c is an additional shape parameter.The Weibull and exponential distributions are the most widely used in the reliability and survival studies. This is due to their simplicity and easy mathematical manipulations. In additions, the exponential distribution is one of the members for Weibull-
and c is an additional shape parameter.The Weibull and exponential distributions are the most widely used in the reliability and survival studies. This is due to their simplicity and easy mathematical manipulations. In additions, the exponential distribution is one of the members for Weibull-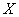 family as well. Let
family as well. Let 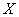 be a random variable taken from exponential distribution with probability density function pdf and cumulative distribution function (CDF) respectively,
be a random variable taken from exponential distribution with probability density function pdf and cumulative distribution function (CDF) respectively, 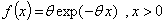 and
and 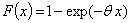 . Also, let
. Also, let 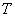 be a random variable taken from Weibull distribution with pdf is
be a random variable taken from Weibull distribution with pdf is 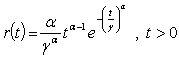 . Then, the pdf of Weibull-Exponential distribution is
. Then, the pdf of Weibull-Exponential distribution is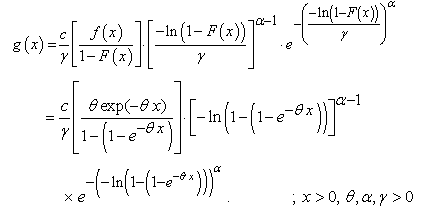
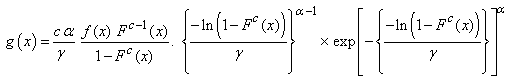
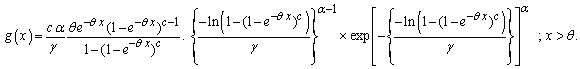
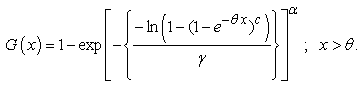
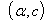 are the shape parameters and
are the shape parameters and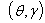 are the scale parameters respectively.In (2.3), note that, if
are the scale parameters respectively.In (2.3), note that, if 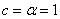 , the pdf of the GWED reduces to the exponential distribution with parameter
, the pdf of the GWED reduces to the exponential distribution with parameter 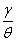 . Also, when
. Also, when 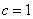 and the GWED reduces to the Weibull distribution with parameters
and the GWED reduces to the Weibull distribution with parameters 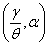 . The exponentiated exponential distribution produced when
. The exponentiated exponential distribution produced when 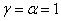 as well.
as well.
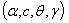 respectively
respectively
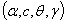 respectively
respectively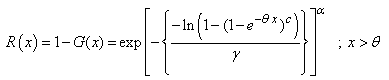
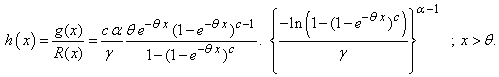
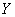 be an Exponentiated Weibull random variable with parameters
be an Exponentiated Weibull random variable with parameters 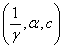 , then, using this transform
, then, using this transform 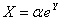 , the result is the pdf for the GWED. Also, if
, the result is the pdf for the GWED. Also, if 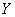 be a standard exponential random variable with parameters
be a standard exponential random variable with parameters 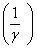 , then, using
, then, using 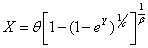 as a transform, the result is the pdf for the GWED. And using the transform
as a transform, the result is the pdf for the GWED. And using the transform 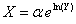 be a random variable for the Exponentiated Frechet distribution to get on the pdf of the GWED.
be a random variable for the Exponentiated Frechet distribution to get on the pdf of the GWED. goes to infinity, and when
goes to infinity, and when  , the limit is given by:
, the limit is given by: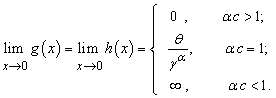

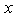 goes to zero, the limit of the quantity between brackets
goes to zero, the limit of the quantity between brackets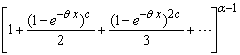 equals one. So, (3.1.2) reduces to:
equals one. So, (3.1.2) reduces to: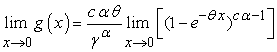
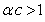 , then, (3.1.3) goes to zero, if
, then, (3.1.3) goes to zero, if 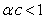 , it goes to infinity and if
, it goes to infinity and if 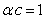 , it reduces to
, it reduces to 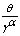 .Lemma 2: The limiting of the hazard function for the GWED when
.Lemma 2: The limiting of the hazard function for the GWED when 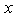 goes to infinity is:
goes to infinity is: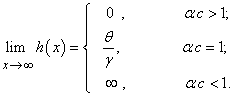
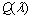 and Shannon entropy
and Shannon entropy 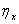 for the Exponentiated T-X distributions by using the CDF for the X and T distributions as follows:
for the Exponentiated T-X distributions by using the CDF for the X and T distributions as follows: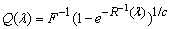
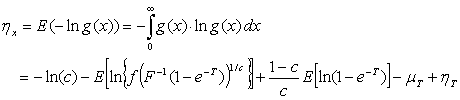
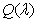 and
and 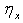 of the GWED respectively are:
of the GWED respectively are: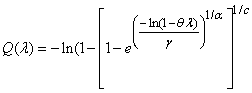
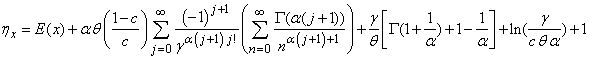
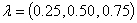 in (3.2.3). Also, based on quartiles, the skewness and kurtosis for the GWED respectively are:
in (3.2.3). Also, based on quartiles, the skewness and kurtosis for the GWED respectively are: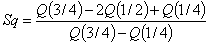
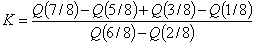
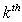 moments of the GWED can be obtained via the moment generating function which can be derived as follows:
moments of the GWED can be obtained via the moment generating function which can be derived as follows: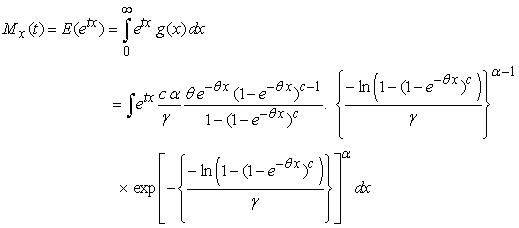
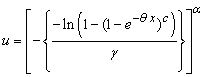 , then,
, then, 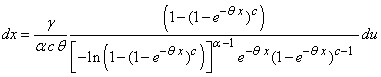 , and the integral in (3.3.1) can be written as:
, and the integral in (3.3.1) can be written as: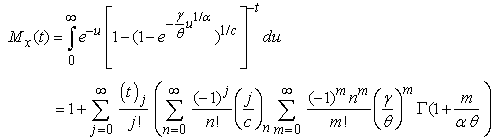
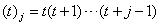 .The result in (3.3.3) came by using the following series expansions:
.The result in (3.3.3) came by using the following series expansions: 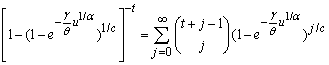 ,
,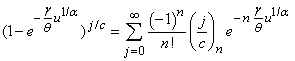 and
and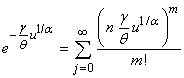 .
.
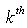 derivative of (3.3.2) and replacing
derivative of (3.3.2) and replacing 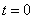 to obtain the
to obtain the 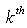 moments. Therefore,
moments. Therefore, 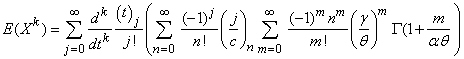
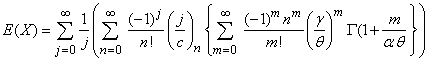
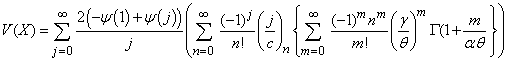
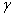 and c increase. And
and c increase. And 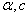 are fixed the mean of GWED is increase while the mean and variance of GWED are decrease.
are fixed the mean of GWED is increase while the mean and variance of GWED are decrease.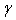 and c increase. And
and c increase. And 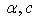 are fixed the mean of GWED is increase while the mean and variance of GWED are decrease.
are fixed the mean of GWED is increase while the mean and variance of GWED are decrease.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML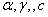 and
and 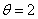 is fixed
is fixed
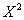 Values for Tribolium Castaneum Cultured at
Values for Tribolium Castaneum Cultured at 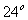 C
C
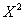 Values for Tribolium Castaneum Cultured at 24℃
Values for Tribolium Castaneum Cultured at 24℃
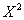 Values for Tribolium Castaneum Cultured at 24℃
Values for Tribolium Castaneum Cultured at 24℃