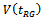-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Statistics and Applications
p-ISSN: 2168-5193 e-ISSN: 2168-5215
2013; 3(3): 71-76
doi:10.5923/j.statistics.20130303.06
On the Variance Estimation of Regression Estimator
N. R. Das1, R. K. Nayak2, L. N. Sahoo1
1Department of Statistics, Utkal University, Bhubaneswar, 751004, India
2Department of Statistics, Khallikote College, Berhampur, 760001, India
Correspondence to: L. N. Sahoo, Department of Statistics, Utkal University, Bhubaneswar, 751004, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper, an attempt has been made to estimate variance of the classical regression estimator. Adopting some available techniques used for estimation of population variance under classical as well as predictive approach, we develop eight new variance estimators of the classical regression estimator. It is assumed that the population mean and population variance of the auxiliary variable are known prior to sampling. A simulation study has been undertaken for evaluating relative performance of the suggested estimators in respect of standard error and coverage rate based on 95% confidence interval.
Keywords: Auxiliary Variable, Confidence Interval, Prediction Approach, Regression Estimator, Stability
Cite this paper: N. R. Das, R. K. Nayak, L. N. Sahoo, On the Variance Estimation of Regression Estimator, International Journal of Statistics and Applications, Vol. 3 No. 3, 2013, pp. 71-76. doi: 10.5923/j.statistics.20130303.06.
Article Outline
1. Introduction
- Consider a finite population
 . Let
. Let 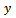 and
and 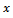 denote the study variable and an auxiliary variable taking values
denote the study variable and an auxiliary variable taking values 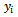 and
and 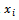 respectively on the ith unit
respectively on the ith unit . Let
. Let ,
,  be the population means and
be the population means and 
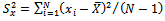 be the population variances of
be the population variances of 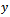 and
and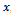 , and
, and 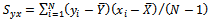 be the population covariance between
be the population covariance between  and
and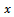 . Consider a sample
. Consider a sample 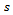 of
of 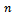 units drawn from
units drawn from  according to simple random sampling without replacement (SRSWOR) to estimate the unknown mean
according to simple random sampling without replacement (SRSWOR) to estimate the unknown mean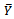 . Let
. Let  and
and 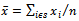 be the sample means,
be the sample means, 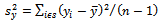 and
and 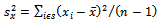 the sample variances, and
the sample variances, and 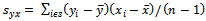 be the sample covariance.The classical regression estimator of
be the sample covariance.The classical regression estimator of 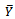 that utilizes known value of
that utilizes known value of 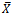 is defined by
is defined by 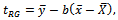 where
where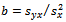 is the familiar least squares estimator of
is the familiar least squares estimator of , the population regression coefficient of
, the population regression coefficient of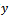 on
on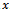 . The main advantages associated with
. The main advantages associated with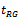 are that it can cover both the situations of positive and negative correlations between
are that it can cover both the situations of positive and negative correlations between and
and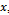 , and its precision is usually higher than that of the simple expansion (direct) estimator
, and its precision is usually higher than that of the simple expansion (direct) estimator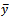 as well as its ratio and product counterparts. In early days regression estimator was not frequently used in practice because of its computational difficulty. But later on, due to advancement of computational facilities, the regression or regression-type estimators are of much interest to the survey statisticians. The approximate variance of
as well as its ratio and product counterparts. In early days regression estimator was not frequently used in practice because of its computational difficulty. But later on, due to advancement of computational facilities, the regression or regression-type estimators are of much interest to the survey statisticians. The approximate variance of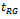 is given by
is given by | (1.1) |
 is the correlation coefficient between
is the correlation coefficient between 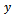 and
and . The precision of
. The precision of is usually discussed in terms of
is usually discussed in terms of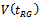 . But the exact value of this variance is unknown as it depends on the unknown population quantities
. But the exact value of this variance is unknown as it depends on the unknown population quantities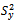 and
and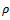 . Hence, the estimation of the variance of
. Hence, the estimation of the variance of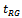 seems to be an important aspect of study in the survey sampling literature. An estimate of the variance is needed to provide a measure of the error in estimation of the mean
seems to be an important aspect of study in the survey sampling literature. An estimate of the variance is needed to provide a measure of the error in estimation of the mean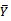 by
by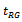 . A variance estimate is also used to construct a confidence interval for the unknown mean. A commonly used estimator of the approximate variance
. A variance estimate is also used to construct a confidence interval for the unknown mean. A commonly used estimator of the approximate variance is its sample analogue
is its sample analogue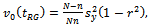 | (1.2) |
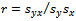 is the sample correlation coefficient, a consistent estimate of
is the sample correlation coefficient, a consistent estimate of . Survey sampling literature provides a number of procedures for estimating unknown variance
. Survey sampling literature provides a number of procedures for estimating unknown variance  using auxiliary information based either on the classical approach [cf., Das and Tripathi[1], Isaki[2], Kadilar and Cingi[3], Grover[4], Yadav[5]] or on the predictive approach [cf., Bolfarine and Zacks[6], Biradar and Singh[7], Nayak and Sahoo[8]]. On the other hand, estimation of correlation coefficient although receives considerable attention in many research papers [cf., Gupta and Singh[9], Shevlyakov[10], Roy[11], Shevlyakov and Smirnov[12]], the sample correlation coefficient
using auxiliary information based either on the classical approach [cf., Das and Tripathi[1], Isaki[2], Kadilar and Cingi[3], Grover[4], Yadav[5]] or on the predictive approach [cf., Bolfarine and Zacks[6], Biradar and Singh[7], Nayak and Sahoo[8]]. On the other hand, estimation of correlation coefficient although receives considerable attention in many research papers [cf., Gupta and Singh[9], Shevlyakov[10], Roy[11], Shevlyakov and Smirnov[12]], the sample correlation coefficient  still remains as the most discussed estimator of
still remains as the most discussed estimator of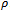 . Hence, our mechanism of estimating
. Hence, our mechanism of estimating 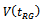 in this work consists of selecting alternative estimators of
in this work consists of selecting alternative estimators of in place of
in place of 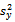 and selecting
and selecting 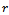 as the estimator of
as the estimator of in the usual way. We assume that both
in the usual way. We assume that both 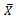 and
and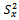 are known accurately.
are known accurately.2. Formulation of the Estimators
- As pointed out earlier, our principal interest here is the estimation of
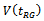 with special concentration on the use of an estimator
with special concentration on the use of an estimator 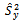 for
for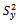 that incorporates the available auxiliary information on
that incorporates the available auxiliary information on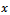 . This means that we focus attention on the creation of variance estimators having the following generalized form:
. This means that we focus attention on the creation of variance estimators having the following generalized form: 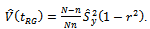 | (2.1) |
 can generate a family of estimators of
can generate a family of estimators of 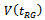 for various selections of
for various selections of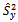 . This goal can be achieved by many alternatives ways. But, the variety of finite population variance estimation methods and variety of estimator selection criteria leave us wondering which estimator could be used successfully. The literature to date also offers little guidance in this choice. However, as we are concerned with the variance estimation, we give more stress on the property of non-negativity of an estimator. It means that we do not consider some estimators of
. This goal can be achieved by many alternatives ways. But, the variety of finite population variance estimation methods and variety of estimator selection criteria leave us wondering which estimator could be used successfully. The literature to date also offers little guidance in this choice. However, as we are concerned with the variance estimation, we give more stress on the property of non-negativity of an estimator. It means that we do not consider some estimators of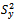 that achieve negative values very frequently under repeated sampling from a given population. Let us now present a brief review of the estimators those are taken into account in the present work. Two notable but simple estimators under classical approach due to Das and Tripathi[1] and Isaki[2] are very much popular in survey practice. These estimators are defined by
that achieve negative values very frequently under repeated sampling from a given population. Let us now present a brief review of the estimators those are taken into account in the present work. Two notable but simple estimators under classical approach due to Das and Tripathi[1] and Isaki[2] are very much popular in survey practice. These estimators are defined by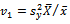 and
and ,respectively. It may be mentioned here that when
,respectively. It may be mentioned here that when ,
, 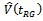 is reduced to the estimator of Deng and Wu[13]. During the years that followed, emphasis has also been given on the prediction of the population variance using auxiliary information. Under this approach, the survey data are at hand i.e., the sample observations are treated as fixed and unassailable. Uncertainty is then attached only to the unobserved values which need to be predicted. To take the advantage of this criterion, the population
is reduced to the estimator of Deng and Wu[13]. During the years that followed, emphasis has also been given on the prediction of the population variance using auxiliary information. Under this approach, the survey data are at hand i.e., the sample observations are treated as fixed and unassailable. Uncertainty is then attached only to the unobserved values which need to be predicted. To take the advantage of this criterion, the population  is decomposed into two mutually exclusive domains
is decomposed into two mutually exclusive domains  and
and 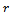 of
of 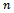 and
and 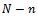 units respectively, where
units respectively, where 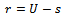 denotes the collection of units in
denotes the collection of units in 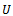 which are not included in s. Biradar and Singh[7], Nayak and Sahoo[8] considered the following predictive equation to predict
which are not included in s. Biradar and Singh[7], Nayak and Sahoo[8] considered the following predictive equation to predict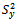 developed earlier by Bolfarine and Zacks[6]:
developed earlier by Bolfarine and Zacks[6]: | (2.2) |
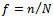 ,
,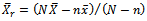 ;
; 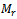 and
and 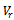 are the implied predictors of
are the implied predictors of  and
and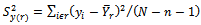 respectively.For different selections of
respectively.For different selections of 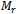 and
and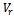 , (2.2) can lead to a number of estimators of
, (2.2) can lead to a number of estimators of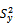 . But, here we report below six estimators viz.,
. But, here we report below six estimators viz., 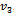 ,
,  ,
,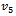 suggested by Biradar and Singh [7], and
suggested by Biradar and Singh [7], and ,
, 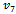 ,
,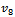 suggested by Nayak and Sahoo[8]:
suggested by Nayak and Sahoo[8]:  After identifying eight estimators of
After identifying eight estimators of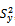 , we then utilize equation (2.1) to produce estimators of
, we then utilize equation (2.1) to produce estimators of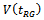 by substituting an estimator
by substituting an estimator fo
fo r. This operation generates eight estimators corresponding to different but specific choices of
r. This operation generates eight estimators corresponding to different but specific choices of as shown in Table 1. To save space, the detail expressions of proposed estimators are not given.
as shown in Table 1. To save space, the detail expressions of proposed estimators are not given. 3. Performance of the Proposed Estimators
- Generally we judge estimators by their design-based qualities, such as design expectation and design variance, under repeated sampling with a given design from the fixed finite population. The regression estimator is no exception. We are thus interested in evaluating the statistical properties of the eight variance estimators i.e.,
 , compared to the traditional estimator
, compared to the traditional estimator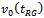 . But, this cannot be done exactly, because of the complex nature of the considered estimators. However, here we rely on a Monte Carlo simulation in which 5000 independent samples for
. But, this cannot be done exactly, because of the complex nature of the considered estimators. However, here we rely on a Monte Carlo simulation in which 5000 independent samples for 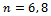 and
and 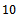 are drawn from 20 populations available in various text books and research papers on survey sampling. The following performance measures of an estimator
are drawn from 20 populations available in various text books and research papers on survey sampling. The following performance measures of an estimator 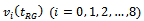 are taken into consideration:(i) Standard Error (SE) : This performance measure of
are taken into consideration:(i) Standard Error (SE) : This performance measure of 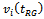 is defined by
is defined by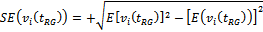 , which is a convenient and widely used indicator of the precision attained by the variance estimator.
, which is a convenient and widely used indicator of the precision attained by the variance estimator.
|
- (ii) Coverage Rate (CR) Based on 95% Confidence Interval for Estimating
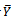 : We consider an approximate 95% confidence interval for
: We consider an approximate 95% confidence interval for 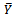 based on
based on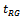 and its variance estimator
and its variance estimator 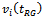 defined by
defined by under the assumption that sampling distribution of
under the assumption that sampling distribution of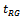 is approximately a normal distribution. This performance measure gives us an idea about which percentage of the so constructed confidence intervals based on the variance estimator covers the true value of
is approximately a normal distribution. This performance measure gives us an idea about which percentage of the so constructed confidence intervals based on the variance estimator covers the true value of 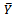 under repeated draws of independent samples from a population.
under repeated draws of independent samples from a population. 4. Description of the Monte Carlo Simulation
- Our Monte Carlo study involves repeated draws of simple random without replacement samples from 20 natural populations. Table 2 presents the source, size
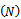 , definitions of the variables y and x in respect of these populations. 5,000 independent samples, for
, definitions of the variables y and x in respect of these populations. 5,000 independent samples, for 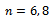 and 10, were selected from each population and for each sample numerical values of the comparable estimators were calculated. Then, considering 5,000 such combinations, simulated values of the performance measures viz., SE and CR were computed and summarized in Tables 3 and 4. Results for
and 10, were selected from each population and for each sample numerical values of the comparable estimators were calculated. Then, considering 5,000 such combinations, simulated values of the performance measures viz., SE and CR were computed and summarized in Tables 3 and 4. Results for are not shown, as they confirm more or less the tendencies found in the cases of
are not shown, as they confirm more or less the tendencies found in the cases of  and 10. Major findings of the study are discussed in subsections 4.1 and 4.2.
and 10. Major findings of the study are discussed in subsections 4.1 and 4.2.4.1. Results Based on the Standard Error
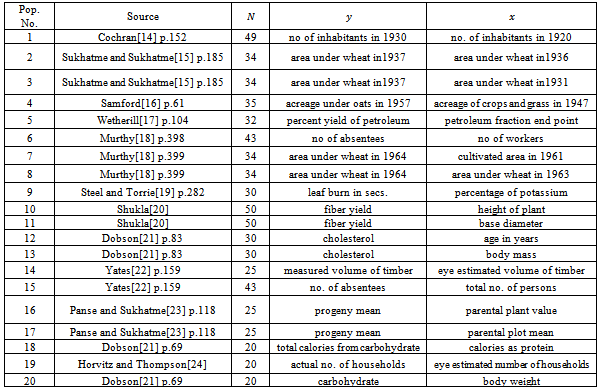
- Simulation results on the SE of the different estimators are provided in Table 3. From these results, as is usually expected, we note that the SE of an estimator diminishes with enlargement of sample size. In respect of this criterion, the performance of
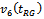 seems to be very poor, and the estimators
seems to be very poor, and the estimators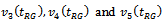 behave very much erratically and there is no clear indication that which one of them would have a decidedly better overall performance than other two estimators. The estimator
behave very much erratically and there is no clear indication that which one of them would have a decidedly better overall performance than other two estimators. The estimator 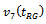 emerged out as the best performer as it is decidedly more efficient than the rest of the estimators in 12 and 9 populations for
emerged out as the best performer as it is decidedly more efficient than the rest of the estimators in 12 and 9 populations for 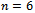 and 10 respectively, and ranked as second in 6 and 9 populations for
and 10 respectively, and ranked as second in 6 and 9 populations for 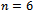 and 10 respectively. However, on this consideration we may choose
and 10 respectively. However, on this consideration we may choose 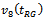 and
and 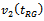 as the second best and third best performers respectively.
as the second best and third best performers respectively. 4.2. Results Based on the Coverage Rate
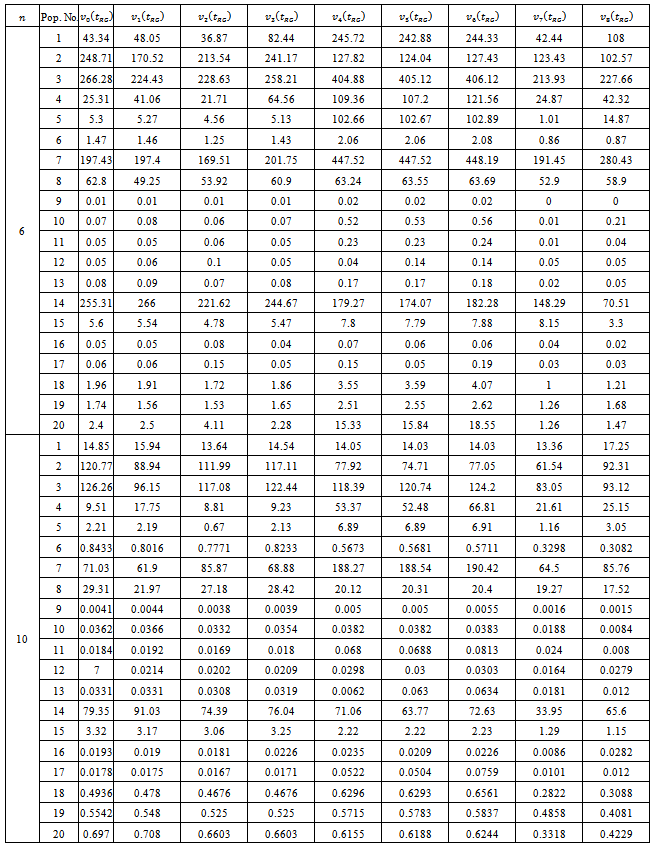
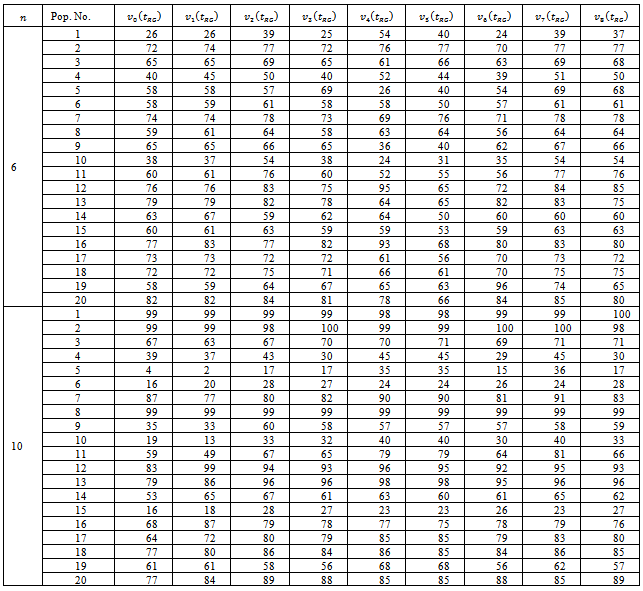
- Using several variance estimators, the coverage rates of nominal 95% confidence intervals for
 are shown in Table 4. The results on the CR give clear indication of improvement in the performance of an estimator as the sample size increases. The CR of the estimators (except some few cases) usually bears no resemblance to the nominal rates aimed at. The three estimators
are shown in Table 4. The results on the CR give clear indication of improvement in the performance of an estimator as the sample size increases. The CR of the estimators (except some few cases) usually bears no resemblance to the nominal rates aimed at. The three estimators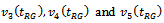 perform equally well. However, on the ground of the achieved CR we may consider
perform equally well. However, on the ground of the achieved CR we may consider 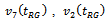 , and
, and  as the best, second best and third best performers respectively.
as the best, second best and third best performers respectively.
|
|
|
5. Conclusions
- Our Monte Carlo simulation study shows that the estimator
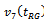 is preferable to its competitors on the grounds of SE and CR. It means that this variance estimator is more efficient than others and can also produce shorter confidence intervals for the population mean. On the other hand, the estimators
is preferable to its competitors on the grounds of SE and CR. It means that this variance estimator is more efficient than others and can also produce shorter confidence intervals for the population mean. On the other hand, the estimators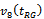 and
and  may be considered as the second best choice on the consideration of SE and CR respectively. Although the conclusions of this Monte Carlo investigation may not be applicable to all situations, they provide certain guidelines on the overall performance of the variance estimators under consideration. Further investigations in this direction with the help of other performance measures may be more useful for better understanding of the statistical properties of the estimators.
may be considered as the second best choice on the consideration of SE and CR respectively. Although the conclusions of this Monte Carlo investigation may not be applicable to all situations, they provide certain guidelines on the overall performance of the variance estimators under consideration. Further investigations in this direction with the help of other performance measures may be more useful for better understanding of the statistical properties of the estimators. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML