1. Introduction

The estimation of population size is of great importance in a variety of biological problems which are related to population growth, ecological adaptation, evolution and so on. The basic technique of capture-recapture (CR) was first introduced by Lincoln (1930)[9] to estimate the total number of duck in North America. The same method was adopted by Jackson (1933)[8] to estimate the true density of tsetse flies. Capture recapture methods have also been successfully applied to natural populations, like, moths by Fisher & Ford (1947)[4] caught, marked and released on several different days. Although in the various papers cited above effective use has been made of estimates of population size and of birth- and death-rates, there has been little discussion for varying capture probability which is obvious in natural population. In fact, equal capture probability is a convenient mathematical model with no empirical justification. Accurate estimation of population size requires with some degree of unequal probabilities of capture. The purpose of the paper is to produce a general model to estimate the size of a closed population allowing the variability of the capture probabilities among animal population. Actually, we present a two stage sampling procedure to estimate the total for a spatially aggregated, moving animal population in a huge study area, like, elephant-population in savanna forest in Africa or vampire bat- population in Central and South America. In this multistage sampling design, we first consider ACS and in the second stage we follow capture recapture (CR) sampling to obtain an estimate of the total of the population where the capture probabilities are varying among animals. In the second section, we discuss the idea of adaptive cluster sampling and then we derived the probability models for the animals with unequal capture probabilities. We derive the estimator for the animal total in each network and at last obtain the estimator of the population size in the study area. We also derive the variance and show the unbiasedness of the estimator.

2. Objective

There are many ways to modify cluster sampling for more complex sampling situations. One common modification is to take a sample of secondary units from within sampled clusters instead of inspecting every secondary unit within each sampled cluster. Estimating the wide variety of animal populations in nature is a complex situation. An efficient sampling procedure for estimating totals and means of rare and clustered populations was proposed by Thompson (1990)[13]. In this model, one is to take an initial sample by some ordinary sampling procedure, and, whenever the variable of interest of a unit in the sample satisfies a previously specified condition, units in the neighbourhood of that unit are added to the sample. If any of the newly added units satisfy the condition, units in their neighbourhoods are also added until the sample includes all the neighbours of any unit satisfying the condition. The ACS technique is appropriate for sampling rare and clustered populations; one of its main drawbacks is the lack of control of the final sample size. Several studies have been done to control the final sample size well, and Salehi & Seber (2002)[12] have proposed a promising estimator of the mean. However, in this paper, we propose a two-stage version in which primary units are selected using a conventional design, and secondary units within the selected primary units are subsampled using adaptive cluster sampling designs. Then capture recapture method is applied. Our proposal, which we have called two stage sampling, requires the availability of an inexpensive and easy-to-measure auxiliary variable, which is used to select a first-phase adaptive cluster sample. The network structure of this first-phase sample is used to select the subsequent subsamples, which are selected using conventional designs. Only the values of the survey variable associated with the units in the final-stage subsample are recorded, and the population total is estimated by a capture recapture type of estimator. Our proposed two stage sampling design will allow the sampler to reach the following goals: to control the number of measurements of the variable of interest; to allocate the final-stage subsample near interesting places; to use the auxiliary variable at network selection; and to use different capture probability among animal population.

3. Methods and Models

We assume that we have a huge study area of N units of same size. Suppose we take a random sample of size n with or without replacement. If an observed sampled unit satisfies the condition of existence of a particular habitat, then the additional units of the neighborhood will be added to the sample. If any of these additional units satisfy the condition again, then the units in their neighborhoods are added to the sample also. The process continues until a cluster of units is obtained that contains a “boundary” of edge units that do not satisfy the condition.

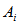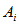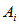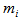We will follow the notations of Thompson and Seber (1996)[15]. Let be the network for sampling unit i, that is, selection of any unit in leads to the selection of all of . Let be the number of sampling units in 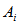. Also let 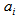be the total number of sampling units in networks of which sampling unit i is an edge unit. If the initial sample is selected without replacement, the probability that unit is included in the sample becomes,

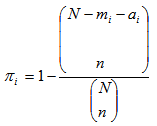(3.1)

If we do not consider the edge units, the partial inclusion probability (1) becomes,

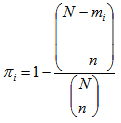(3.2)

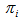If the probability, (2) is known for all sampled units, we can use Horvitz-Thompson estimator (1952)[7] to estimate the population total, 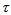, namely,

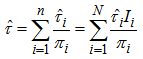(3.3)

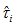In the above expression, is the estimator of the total in the ith network and 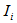takes 1 when the unit i is included in the sample, another words, if the initial sample intersects 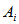(with probability 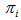) and 0 otherwise.

If the initial sample is selected with replacement, then Hansen-Hurwitz estimator of the population total is suggested, see, Hansen and Hurwitz (1943)[6]. Now the probability of selecting ith unit, 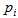is known and the inclusion probability becomes,

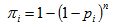(3.4)

The Hansen-Hurwitz estimator of the population total is given by,

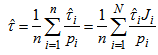(3.5)

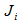In Hansen-Hurwitz estimator[11], is the number of times unit I is selected and 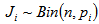.The final sample then consists of n clusters, one for each unit selected in the initial sample. We apply a variable capture probability model in each network.

Notation and the model

In second stage of the model, we consider a closed population and derive an estimator to estimate the animal population size in a single network. This model allows variability in capture probabilities among animals[1]. The source of variation in the capture probabilities is the heterogeneity among individuals. This model is applicable when the time difference between two the trapping occasions is short, such as consecutive days. Here the population size in the ith network is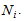

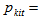The capture probability of the kth animal at t capture occasion in the ith network.

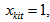If the kth animal is caught at t capture occasion in the ith network and 0 otherwise.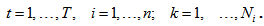

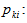A random sample from F.

We have a data matrix of dimension, .

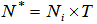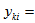The number of times the kth animal is captured in the ith network.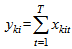

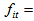The number of animals captured exactly t-times in the ith network.

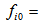The number of animals never capture in the ith network.

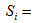The number of animals has been seen at least once during the trapping occasion in the ith network.

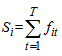Assumptions

1. The population at risk of capture is closed and is of size

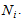2. 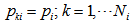is a random sample from a probability distribution F.

3. The random variables 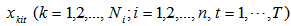are mutually independent for given .

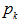In N* matrix, we can only observe Si rows and it allows the calculations of the capture-recapture statistics of the unobserved rows are all zeros. The joint conditional distribution of 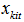is[1],

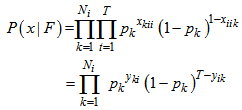Since this probability distribution is not useful for estimation of N_i , we consider p_i = p as a random sample and average over it to obtain the capture distribution of ,

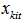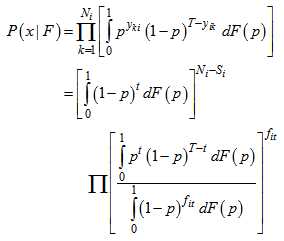For this model, the capture frequencies is the set of sufficient statistics and sufficiency holds for the entire class of distributions F of capture probabilities. Because of this, nonparametric method is applicable to estimate the population size. The unconditional distribution of the capture frequencies is,

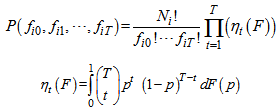Application of Jackknife estimator to estimate the population total

This method was first introduced by Gray and Schucany (1972). Let the initial estimator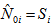, the number of animals captured in the ith network. Here 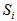is the nonparametric maximum likelihood estimator of 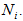Again is biased and the bias decreases as T increases.

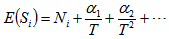Here 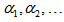are constants. Here 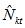is a linear combination of capture frequencies and it is minimal sufficient statistic. It follows from elementary properties of the multinomial distribution[7] that

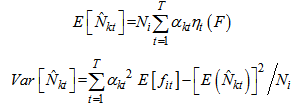After finding the U-statistics, the Jackknife estimators becomes,

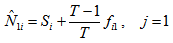, the order of Jackknife estimator.

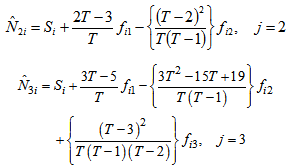Actually, 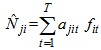is a linear combination of the capture frequencies which is are minimal sufficient statistics.

Now the estimated animal total in the study area becomes,

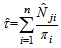Here the initial sample is selected by SRS without replacement with inclusion probability,

If the initial sample is selected by SRS with replacement, the estimator becomes,

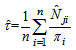Properties

In this two stage sampling, is a biased estimator with population total with variance,

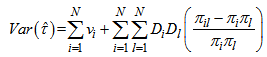Where,

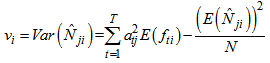And,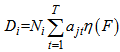

4. Discussion

This paper is a kind of outline of an ongoing research work. We still need to check the mathematical properties of the developed models by simulation study. We find that is would be extremely appropriate if we could show a real life application of this model. If it is not possible to collect data in from the real world, we are planning to perform a simulation study.