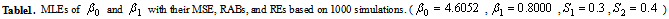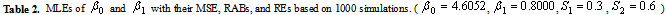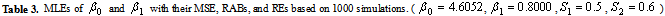Shashi Saxena, Shazia Zarrin, Mustafa Kamal, Arif-Ul-Islam
Department of Statistics & Operations Research Aligarh Muslim University Aligarh, India
Correspondence to: Shashi Saxena, Department of Statistics & Operations Research Aligarh Muslim University Aligarh, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Accelerated testing is needed when testing even large sample sizes at use stress would yield few or no failures within a reasonable time. The step-stress accelerated life test is used to increase the stress levels at fixed times during the experiment. This paper deals with the problem of designing an optimum step stress accelerated life test for Rayleigh distribution. The scale parameter of the distribution is assumed to be a log linear function of stress. The maximum likelihood estimates of the parameters under consideration are obtained. Interval estimation that generates narrow intervals to the unknown parameters of the distribution with high probability is obtained. Optimization criterion is also discussed and simulation results are obtained to explain the techniques used in the paper.
Keywords:
Cumulative Exposure Model, Asymptotic Variance, Fisher Information Matrix, Maximum Likelihood Estimator
Cite this paper: Shashi Saxena, Shazia Zarrin, Mustafa Kamal, Arif-Ul-Islam, Optimum Step Stress Accelerated Life Testing For Rayleigh Distribution, International Journal of Statistics and Applications, Vol. 2 No. 6, 2012, pp. 120-125. doi: 10.5923/j.statistics.20120206.05.
1. Introduction
With today's high technology, some life tests result in none or very few failures, by the end of the test. In such cases, an approach is to do life test at higher-than-usual stress conditions, in order to obtain failures quickly. This can be achieved by using accelerated life test (ALT). ALT is achieved by subjecting units and components to test conditions such that failure occurs sooner. Thus, prediction of the long-term reliability can be made within a short period of time. Results from the ALT are used to extrapolate the unit characteristics at any future time and given at normal operating conditions.ALT can be applied only when a model relating life length to stress is known. One way to accelerate failure is step-stress which increases the stress applied to test product in a specified discrete sequence. Generally, as indicated by Xiong and Ji[1], a test unit starts at a certain low stress. If the unit does not fail at a particular time, stress on it is raised and held at a specified time. Stress is repeatedly increased and held, until the test unit fails or a censoring point is reached.Miller and Nelson[2] described an optimum simple step-stress plan for ALT when failure times are exponentially distributed. Arrhenius inverse-power law played a prominent role in modeling in the paper by Schatzoff and Lane[3]. Bai, Kim, and Lee[4] extended the results of Miller and Nelson[2] to the case of exponential censoring. Nelson[5] has provided a very good survey on the SSALT. Zarrin et al.[6] obtained a 2 step step-stress test plan for exponentiated Weibull distribution. Tang et al.[7] have used a linear cumulative exposure model to analyze data from a SSALT using 3-parameter Weibull distribution. In the paper by Khamis and Higgins[8] an optimum 3 step step-stress test plan has been proposed when the failure time distribution is exponential and the life stress relationship is linear or quadratic. Bhattacharyya and Soejoeti[9] developed a tampered failure-rate model. Bhattacharyya[10] also derived an approach using a Gaussian stochastic process which was later modified and extended by Doksum and Hoyland[11] and Lu and Storer[12]The Rayleigh distribution has played an important role in modeling the lifetime of random phenomena. It arises in many areas of applications, including reliability, life testing and survival analysis. Rayleigh distribution is a special case of Weibull distribution (shape parameter=2) and is frequently used to model wave heights in oceanography, and in communication theory to describe hourly median and instantaneous peak power of received radio signals. It has been used to model the frequency of different wind speeds over a year and a wind turbine sites. The distance from one individual to its nearest neighbor when the spatial pattern is generated by Poisson distribution follows a Rayleigh distribution. In communication theory, Rayleigh distribution is used to model scattered signals that reach a receiver by multiple paths. Depending on the density of scatter, the signal will display different fading characteristics. Rayleigh distribution is used to model dense scatter.Other than this introductory section, this paper includes six more sections. Section 2 deals with the model and assumptions. In section 3 likelihood estimates of parameters and fisher information matrix is evaluated. Confidence intervals for the model parameters based on the asymptotic normality of the MLE are obtained in section 4. Optimization criterion is discussed in section 5. For illustration of the article a simulation study is given in section 6, followed by some concluding remarks in section 7.
2. The Model
The life time of a product at any level of stress is assumed to follow Rayleigh distribution. The scale parameter of the distribution is assumed to be a log linear function of stress. The probability density function (p.d.f.) of Rayleigh distribution is given by Cumulative distribution function (c.d.f) is given by
Cumulative distribution function (c.d.f) is given by where
where 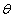 is the scale parameter. The corresponding survival function is
is the scale parameter. The corresponding survival function is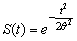 The hazard function of
The hazard function of 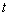 , denoted as
, denoted as 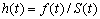 is obtained as
is obtained as 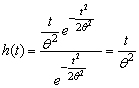 Assumptions The following assumptions are made1. Under any constant stress, the failure time of a test unit follows a Rayleigh distribution with c.d.f. given by
Assumptions The following assumptions are made1. Under any constant stress, the failure time of a test unit follows a Rayleigh distribution with c.d.f. given by  2. The scale parameter
2. The scale parameter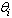 at stress level
at stress level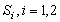 is a log linear function of stress, that is,
is a log linear function of stress, that is, 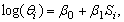 where
where 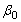 and
and 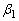 are unknown parameters depending upon the nature of the product and the method of the test.3. The test is conducted as follows: All
are unknown parameters depending upon the nature of the product and the method of the test.3. The test is conducted as follows: All 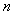 units are initially put on lower stress
units are initially put on lower stress 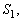 and run until time
and run until time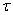 . Then the stress is changed to the high level
. Then the stress is changed to the high level 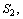 and the test continues until all units fail.4. Total of
and the test continues until all units fail.4. Total of 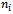 failures are observed at time
failures are observed at time 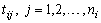 and level
and level 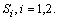 5. The lifetimes of the test units are i.i.d.6. The cumulative exposure model of time to failure step- stress ALT is given by
5. The lifetimes of the test units are i.i.d.6. The cumulative exposure model of time to failure step- stress ALT is given by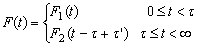 where the equivalent starting time,
where the equivalent starting time, 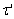 , is a solution of
, is a solution of 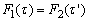 solving for
solving for 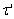 , then
, then 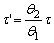 . Thus the Rayleigh cumulative exposure model for simple-stress is given by
. Thus the Rayleigh cumulative exposure model for simple-stress is given by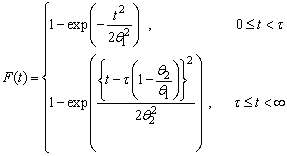 and the corresponding probability density function of the failure time is obtained as
and the corresponding probability density function of the failure time is obtained as 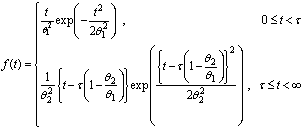
3. Likelihood Function and Fisher Information Matrix
In order to obtain the maximum likelihood estimate (MLE) of the model parameters, let 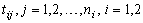 be the observed failure time of a test unit
be the observed failure time of a test unit  under stress level
under stress level 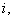 where
where 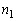 denotes the number of units failed at the low stress
denotes the number of units failed at the low stress 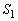 and
and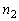 denotes the number of units failed at the high stress
denotes the number of units failed at the high stress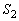 . The likelihood function is given by
. The likelihood function is given by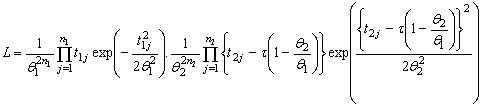 | (1) |
The log likelihood function is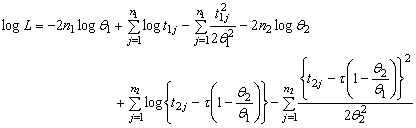 | (2) |
By using the relation 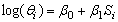
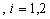 the log likelihood function (2) becomes
the log likelihood function (2) becomes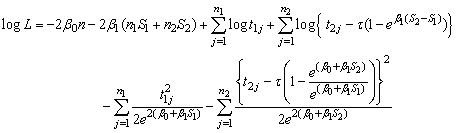 | (3) |
where 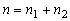 Differentiating eq. (3) partially with respect to
Differentiating eq. (3) partially with respect to  and
and 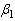 we get
we get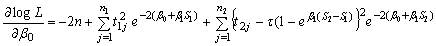 | (4) |
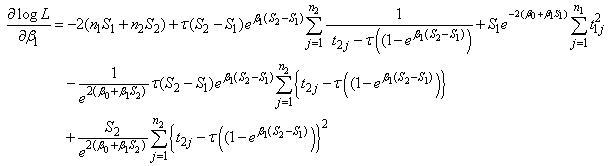 | (5) |
Where MLEs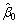 and
and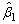 for the model parameters
for the model parameters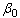 and
and 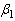 are the value which maximize the likelihood function (1). (4) and (5) are very complex non-linear equations to be solved. Therefore, an iterative procedure is required to solve these equations numerically. Newton Raphson method is used to obtain the MLEs of
are the value which maximize the likelihood function (1). (4) and (5) are very complex non-linear equations to be solved. Therefore, an iterative procedure is required to solve these equations numerically. Newton Raphson method is used to obtain the MLEs of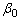 and
and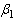 . Once the value of
. Once the value of 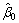 is obtained,
is obtained, 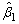 can easily be calculated by using (5).But the exact mathematical expression for the expectation is too difficult to find. So it can be approximated by numerically inverting the asymptotic fisher information matrix. It is composed of the negative second and mixed derivatives of the normal logarithm of the likelihood function evaluated at the MLE. So, asymptotic fisher information matrix can be written as
can easily be calculated by using (5).But the exact mathematical expression for the expectation is too difficult to find. So it can be approximated by numerically inverting the asymptotic fisher information matrix. It is composed of the negative second and mixed derivatives of the normal logarithm of the likelihood function evaluated at the MLE. So, asymptotic fisher information matrix can be written as 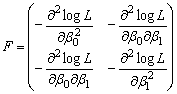 where,
where,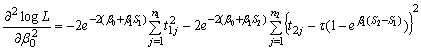
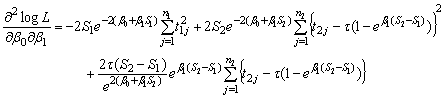
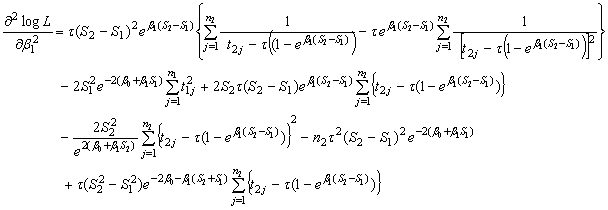
4. Confidence Intervals for Model Parameters
The most common method to set confidence bounds for the parameters is to use asymptotic normal distribution of maximum likelihood estimators, see Vander Wiel and Meeker [13].To construct a confidence interval for a population parameter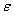 ; assume that
; assume that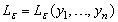 and
and 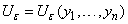 are functions of the sample data
are functions of the sample data 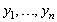 such that
such that 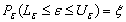 where the interval
where the interval 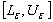 is called a two sided
is called a two sided 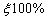 confidence interval for
confidence interval for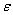 .
. 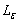 and
and 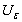 are the lower and upper confidence limits for
are the lower and upper confidence limits for 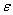 , respectively. The random limits
, respectively. The random limits 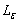 and
and 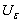 enclose
enclose 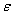 with probability
with probability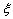 .Asymptotically, the maximum likelihood estimators, under appropriate regularity conditions are consistent and normally distributed. Therefore, the two sided approximate
.Asymptotically, the maximum likelihood estimators, under appropriate regularity conditions are consistent and normally distributed. Therefore, the two sided approximate 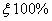 confidence limits for a population parameter
confidence limits for a population parameter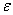 can be constructed such that:
can be constructed such that: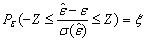 where
where 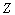 is the
is the 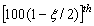 standard normal percentile. Therefore, the two sided approximate
standard normal percentile. Therefore, the two sided approximate 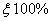 confidence limits for
confidence limits for 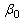 and
and 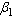 are given respectively as follows:
are given respectively as follows: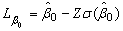
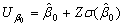
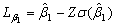
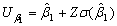
5. Optimization Criterion
The optimal test plan is to determine the duration of the lower stress level. According to Al-Haj Ebrahem and Al-Masri[14], an optimum test plan can be determined with respect to the change time, the asymptotic variance (AV) of the MLE of a given 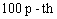 percentile at the design stress
percentile at the design stress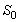 . The log of the
. The log of the 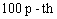 percentile of the lifetime
percentile of the lifetime 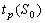 the design stress
the design stress 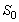 is given by
is given by 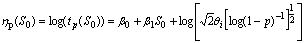 Generally, the optimization criterion is defined to minimize the asymptotic variance of the percentile estimate at the design stress. The MLE is used for the percentile estimate. Then, the AV of the percentile estimate at the design stress can be obtained as follows:
Generally, the optimization criterion is defined to minimize the asymptotic variance of the percentile estimate at the design stress. The MLE is used for the percentile estimate. Then, the AV of the percentile estimate at the design stress can be obtained as follows: 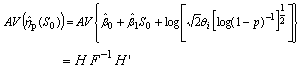 where F is the Fisher information matrix given in Section (3), and
where F is the Fisher information matrix given in Section (3), and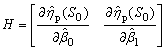 Then
Then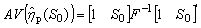
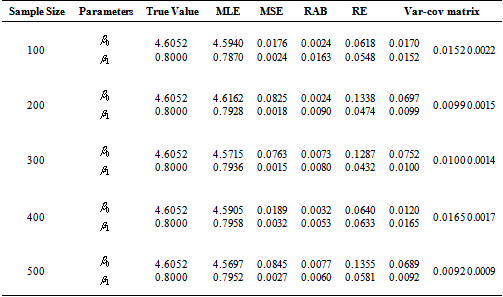
6. Simulation Study
In optimum test plan the duration of the lower stress level is obtained by minimizing the AV of the MLE. But it is very difficult to study the complex derived equations. So a simulation study is performed using Newton-Raphson method to explain the results obtained in the study. MLE, Mean Square Error (MSE), Random absolute Bias (RAB) and Relative Error (RE) and elements of variance covariance matrix are calculated for the given values of the parameters. The steps of simulation procedure are as follows1. Given values of the parameters 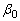 and
and 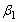 are 4.6052 and 0.8 and stresses
are 4.6052 and 0.8 and stresses 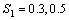 and
and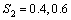 .2. Random samples of size
.2. Random samples of size 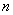 are generated from cumulative exposure model.3. MLEs
are generated from cumulative exposure model.3. MLEs 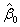 and
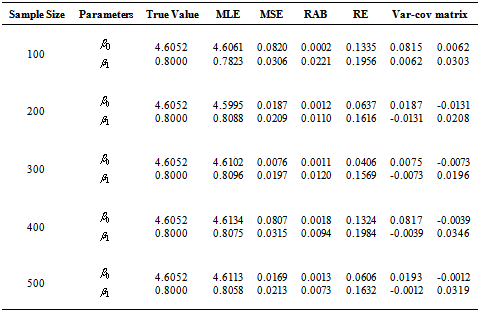
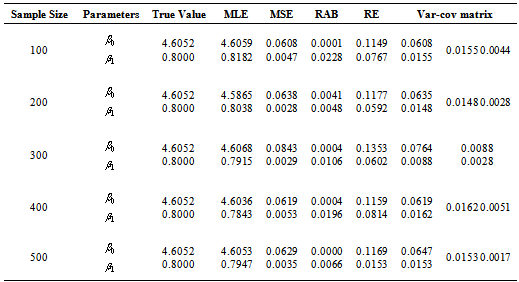
and 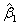 are obtained for each sample size and selected values of the parameters using (4) and (5).4. Some measures of accuracy like MSE, RABs and REs are calculated for all sample size and for different combinations of stresses.5. The resulting estimates of parameters are used to obtain the variance covariance matrix.The results obtained in the above simulation study are summarized in Table 1, 2 and 3. All the three tables show the MLE, MSE, RAB and RE of the estimators for different combinations of stresses. True values of the parameters are taken as
are obtained for each sample size and selected values of the parameters using (4) and (5).4. Some measures of accuracy like MSE, RABs and REs are calculated for all sample size and for different combinations of stresses.5. The resulting estimates of parameters are used to obtain the variance covariance matrix.The results obtained in the above simulation study are summarized in Table 1, 2 and 3. All the three tables show the MLE, MSE, RAB and RE of the estimators for different combinations of stresses. True values of the parameters are taken as 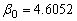 and
and 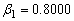 . Table 1 shows different measures for stress combination
. Table 1 shows different measures for stress combination 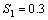 and
and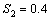 . Similarly table 2 and 3 show the various results for stress combination
. Similarly table 2 and 3 show the various results for stress combination 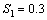 ,
, 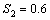 and
and 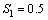 ,
, 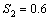 respectively. From these tables the following observations can be made on the performance of SSALT parameter estimation of Rayleigh distribution1. For the first set of stresses (
respectively. From these tables the following observations can be made on the performance of SSALT parameter estimation of Rayleigh distribution1. For the first set of stresses (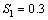 ,
,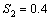 ) the maximum likelihood estimators have good statistical properties than the second (
) the maximum likelihood estimators have good statistical properties than the second (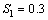 ,
,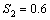 ) and third (
) and third (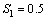 ,
,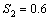 ) set for all sample sizes.2. As the value of stresses increase the estimates have smaller MSE and RE. As the sample size increases the RABs and MSEs of the estimated parameters decrease on an average. This indicates that the maximum likelihood estimates provide asymptotically normally distributed and consistent estimator for the parameters.3. The asymptotic variances of the estimators are decreasing when the sample size increasing.
) set for all sample sizes.2. As the value of stresses increase the estimates have smaller MSE and RE. As the sample size increases the RABs and MSEs of the estimated parameters decrease on an average. This indicates that the maximum likelihood estimates provide asymptotically normally distributed and consistent estimator for the parameters.3. The asymptotic variances of the estimators are decreasing when the sample size increasing.
7. Discussion and conclusions
ALTs are used to estimate the lifetime of highly reliable products within a reasonable testing time. The test units are run at higher than usual levels of stress to induce early failures. The test data obtained at the accelerated conditions are analyzed in terms of a model and then extrapolated to design stress to estimate the life time distribution. This study considered the inference on the parameters and optimally designing simple step stress plan for the Rayleigh distribution. The MLEs of the model parameters were obtained. Performance of step stress testing plans and model assumptions are usually evaluated by the properties of the MLEs of model parameters.In this study the parameters have good statistical properties for the first set of stresses than the other two sets for all sample sizes. Maximum likelihood estimators are consistent and asymptotically normally distributed. As the sample sizes increase the asymptotic variance and covariance of estimators decrease. Here, some final discussions about the results in the study are given. First, a statistical methodology is presented to analyze the data obtained from a step stress accelerated life test. This methodology will be especially useful when intermittent inspection is the only feasible way of checking the status of test units during a step stress test. Second, although the cumulative exposure model has been a popular choice for the analysis of step stress life test data, its validity in various situations remain to be tested. Third, for a simple step stress test, we have derived the optimum choice for the stress change time which minimizes AV under a Rayleigh distribution. This optimum design is particularly important at the designing stage of the test as it gives a guide to experimenters about when the intermittent inspection and the stress change should be carried out during the test. The results on the optimum design are based on the assumption of Rayleigh distribution but its sensitivity is not addressed in this study. These questions provide the direction of future research in this area associated with the data obtained from SSALT is to study the statistical analysis and the optimum design when the stress change time is random variable: such as the order statistics at the current stress levels and when only these order statistics are observed during testing.
References
| [1] | Xiong C, Ji M (2004). Analysis of Grouped and Censored Data from Step-Stress Life Test. IEEE Trans. Reliability., 53(1): 22-28. |
| [2] | Miller, R. and Nelson, W. (1983) ‘Optimum step stress plans for accelerated life testing’, IEEE Trans Reliab vol. 32, pp.59–65. |
| [3] | Schatzoff, M. and Lane, T.P. ( August 1987) ‘A general step stress model for accelerated life testing’, presented at the Joint Statistical Meeting, San Francisco. |
| [4] | Bai, D.S., Kim, M.S. and Lee, S. (1989) ‘Optimum simple step-stress accelerated life tests with censoring’, IEEE Trans Reliab vol. 38, pp.528–532. |
| [5] | Nelson, W. (1990) ‘Accelerated testing: Statistical models, test plans and data analyses’, Wiley Interscience, New York. |
| [6] | Zarrin, S., Saxena, S., and Islam, A. (2010): Step-Stress Accelerated life testing for Exponentiated Weibull distribution. The Journal of the Safety and Reliability Society, 30(3): 5-13. |
| [7] | Tang, L.C., Sun, L.C., Goh, T.N. and Ong, H.L. (1996) ‘Analysis of step-stress accelerated-life-test data: A new approach’, IEEE Trans Reliab vol. 45(1), pp.69–74. |
| [8] | Khamis, I.H. and Higgins, J.J. (1996) ‘Optimum 3-step step-stress tests’, IEEE Trans Reliab vol. 45, pp.341–345. |
| [9] | Bhattacharyya, G.K. and Soejoeti, Z. (1989) ‘A tampered failure rate model for step-stress accelerated life test’, Communications in Statistics: Theory and Methods, vol. 18, pp.1627–1643. |
| [10] | Bhattacharyya, G.K. (1986) ‘Parametric models and inference procedures for accelerated life tests’, presented as an invited paper for 46th session of the International Statistical Institute Meeting,Tokyo, Japan, 8–16 September 1986. |
| [11] | Doksum, K.A. and Hoyland, A. (1991) ‘Models for variable-stress accelerated life testing experiments based on Wiener process and inverse Gaussian distribution’, Technometrics, vol. 34, pp.74–82. |
| [12] | Lu, Y. and Storer, B. (2001), ‘A tampered Brownian motion process mode for partial step-stress accelerated life testing’, Journal of Statistical Planning and Inference, vol. 94, pp.15–24. |
| [13] | Vander Wiel, S.A. and Meeker, W.Q. (1990), .Accuracy of Approximate Confidence Bounds using Censored Weibull Regression Data from Accelerated Life Tests., IEEE Tran. on Reliability, 39(3), August, 346-351. |
| [14] | Al-Haj Ebrahem, M. and Al-Masri, A. (2007) ‘Optimum simple step-stress plan for log-logistic cumulative exposure model’, METRON-International Journal of Statistics, vol. 1, pp.23-34. |

 Cumulative distribution function (c.d.f) is given by
Cumulative distribution function (c.d.f) is given by where
where 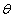 is the scale parameter. The corresponding survival function is
is the scale parameter. The corresponding survival function is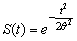 The hazard function of
The hazard function of 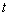 , denoted as
, denoted as 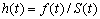 is obtained as
is obtained as 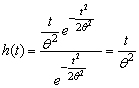 Assumptions The following assumptions are made1. Under any constant stress, the failure time of a test unit follows a Rayleigh distribution with c.d.f. given by
Assumptions The following assumptions are made1. Under any constant stress, the failure time of a test unit follows a Rayleigh distribution with c.d.f. given by  2. The scale parameter
2. The scale parameter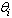 at stress level
at stress level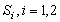 is a log linear function of stress, that is,
is a log linear function of stress, that is, 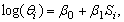 where
where 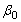 and
and 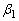 are unknown parameters depending upon the nature of the product and the method of the test.3. The test is conducted as follows: All
are unknown parameters depending upon the nature of the product and the method of the test.3. The test is conducted as follows: All 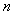 units are initially put on lower stress
units are initially put on lower stress 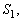 and run until time
and run until time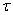 . Then the stress is changed to the high level
. Then the stress is changed to the high level 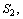 and the test continues until all units fail.4. Total of
and the test continues until all units fail.4. Total of 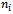 failures are observed at time
failures are observed at time 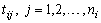 and level
and level 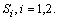 5. The lifetimes of the test units are i.i.d.6. The cumulative exposure model of time to failure step- stress ALT is given by
5. The lifetimes of the test units are i.i.d.6. The cumulative exposure model of time to failure step- stress ALT is given by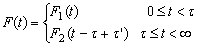 where the equivalent starting time,
where the equivalent starting time, 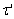 , is a solution of
, is a solution of 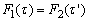 solving for
solving for 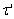 , then
, then 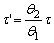 . Thus the Rayleigh cumulative exposure model for simple-stress is given by
. Thus the Rayleigh cumulative exposure model for simple-stress is given by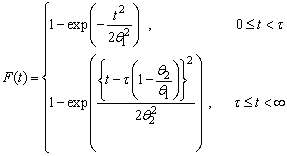 and the corresponding probability density function of the failure time is obtained as
and the corresponding probability density function of the failure time is obtained as 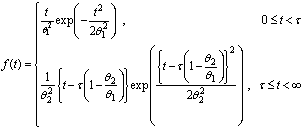
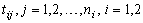 be the observed failure time of a test unit
be the observed failure time of a test unit 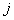 under stress level
under stress level 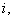 where
where 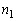 denotes the number of units failed at the low stress
denotes the number of units failed at the low stress 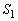 and
and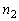 denotes the number of units failed at the high stress
denotes the number of units failed at the high stress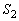 . The likelihood function is given by
. The likelihood function is given by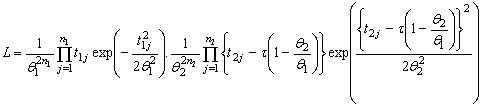
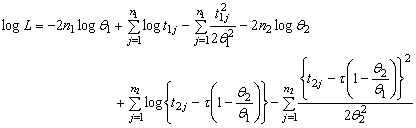
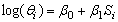
 the log likelihood function (2) becomes
the log likelihood function (2) becomes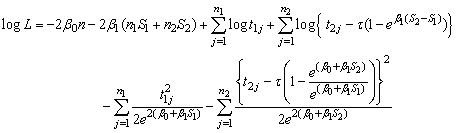
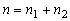 Differentiating eq. (3) partially with respect to
Differentiating eq. (3) partially with respect to 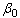 and
and 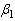 we get
we get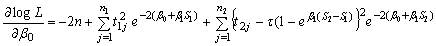
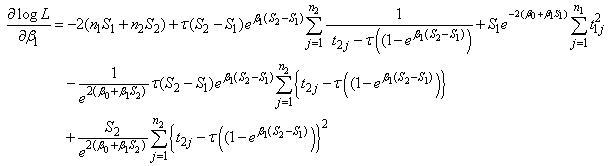
 and
and for the model parameters
for the model parameters and
and 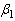 are the value which maximize the likelihood function (1). (4) and (5) are very complex non-linear equations to be solved. Therefore, an iterative procedure is required to solve these equations numerically. Newton Raphson method is used to obtain the MLEs of
are the value which maximize the likelihood function (1). (4) and (5) are very complex non-linear equations to be solved. Therefore, an iterative procedure is required to solve these equations numerically. Newton Raphson method is used to obtain the MLEs of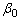 and
and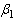 . Once the value of
. Once the value of 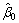 is obtained,
is obtained, 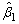 can easily be calculated by using (5).But the exact mathematical expression for the expectation is too difficult to find. So it can be approximated by numerically inverting the asymptotic fisher information matrix. It is composed of the negative second and mixed derivatives of the normal logarithm of the likelihood function evaluated at the MLE. So, asymptotic fisher information matrix can be written as
can easily be calculated by using (5).But the exact mathematical expression for the expectation is too difficult to find. So it can be approximated by numerically inverting the asymptotic fisher information matrix. It is composed of the negative second and mixed derivatives of the normal logarithm of the likelihood function evaluated at the MLE. So, asymptotic fisher information matrix can be written as 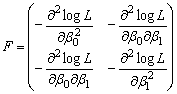 where,
where,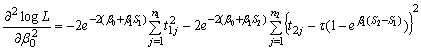
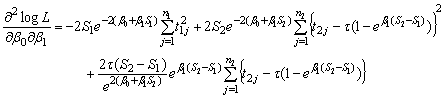
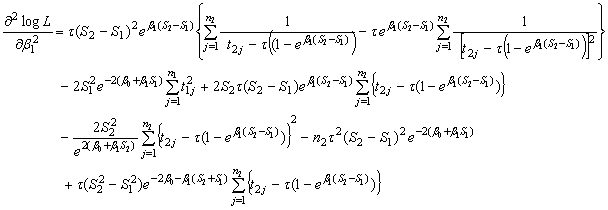
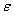 ; assume that
; assume that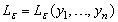 and
and 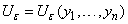 are functions of the sample data
are functions of the sample data 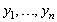 such that
such that 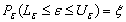 where the interval
where the interval 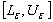 is called a two sided
is called a two sided 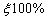 confidence interval for
confidence interval for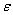 .
. 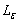 and
and 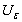 are the lower and upper confidence limits for
are the lower and upper confidence limits for 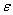 , respectively. The random limits
, respectively. The random limits 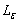 and
and 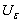 enclose
enclose 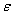 with probability
with probability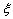 .Asymptotically, the maximum likelihood estimators, under appropriate regularity conditions are consistent and normally distributed. Therefore, the two sided approximate
.Asymptotically, the maximum likelihood estimators, under appropriate regularity conditions are consistent and normally distributed. Therefore, the two sided approximate 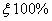 confidence limits for a population parameter
confidence limits for a population parameter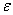 can be constructed such that:
can be constructed such that: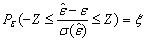 where
where 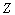 is the
is the 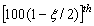 standard normal percentile. Therefore, the two sided approximate
standard normal percentile. Therefore, the two sided approximate 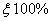 confidence limits for
confidence limits for 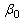 and
and 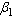 are given respectively as follows:
are given respectively as follows: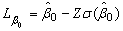
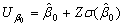
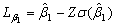
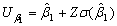
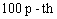 percentile at the design stress
percentile at the design stress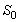 . The log of the
. The log of the 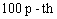 percentile of the lifetime
percentile of the lifetime 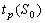 the design stress
the design stress 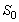 is given by
is given by 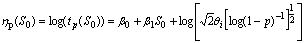 Generally, the optimization criterion is defined to minimize the asymptotic variance of the percentile estimate at the design stress. The MLE is used for the percentile estimate. Then, the AV of the percentile estimate at the design stress can be obtained as follows:
Generally, the optimization criterion is defined to minimize the asymptotic variance of the percentile estimate at the design stress. The MLE is used for the percentile estimate. Then, the AV of the percentile estimate at the design stress can be obtained as follows: 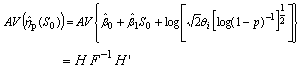 where F is the Fisher information matrix given in Section (3), and
where F is the Fisher information matrix given in Section (3), and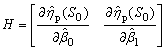 Then
Then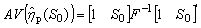
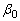 and
and 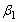 are 4.6052 and 0.8 and stresses
are 4.6052 and 0.8 and stresses 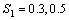 and
and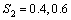 .2. Random samples of size
.2. Random samples of size 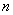 are generated from cumulative exposure model.3. MLEs
are generated from cumulative exposure model.3. MLEs 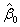 and
and 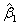 are obtained for each sample size and selected values of the parameters using (4) and (5).4. Some measures of accuracy like MSE, RABs and REs are calculated for all sample size and for different combinations of stresses.5. The resulting estimates of parameters are used to obtain the variance covariance matrix.The results obtained in the above simulation study are summarized in Table 1, 2 and 3. All the three tables show the MLE, MSE, RAB and RE of the estimators for different combinations of stresses. True values of the parameters are taken as
are obtained for each sample size and selected values of the parameters using (4) and (5).4. Some measures of accuracy like MSE, RABs and REs are calculated for all sample size and for different combinations of stresses.5. The resulting estimates of parameters are used to obtain the variance covariance matrix.The results obtained in the above simulation study are summarized in Table 1, 2 and 3. All the three tables show the MLE, MSE, RAB and RE of the estimators for different combinations of stresses. True values of the parameters are taken as 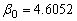 and
and 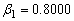 . Table 1 shows different measures for stress combination
. Table 1 shows different measures for stress combination 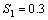 and
and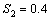 . Similarly table 2 and 3 show the various results for stress combination
. Similarly table 2 and 3 show the various results for stress combination 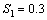 ,
, 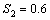 and
and 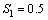 ,
, 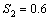 respectively. From these tables the following observations can be made on the performance of SSALT parameter estimation of Rayleigh distribution1. For the first set of stresses (
respectively. From these tables the following observations can be made on the performance of SSALT parameter estimation of Rayleigh distribution1. For the first set of stresses (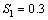 ,
,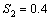 ) the maximum likelihood estimators have good statistical properties than the second (
) the maximum likelihood estimators have good statistical properties than the second (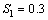 ,
,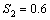 ) and third (
) and third (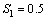 ,
,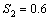 ) set for all sample sizes.2. As the value of stresses increase the estimates have smaller MSE and RE. As the sample size increases the RABs and MSEs of the estimated parameters decrease on an average. This indicates that the maximum likelihood estimates provide asymptotically normally distributed and consistent estimator for the parameters.3. The asymptotic variances of the estimators are decreasing when the sample size increasing.
) set for all sample sizes.2. As the value of stresses increase the estimates have smaller MSE and RE. As the sample size increases the RABs and MSEs of the estimated parameters decrease on an average. This indicates that the maximum likelihood estimates provide asymptotically normally distributed and consistent estimator for the parameters.3. The asymptotic variances of the estimators are decreasing when the sample size increasing. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML