J. Subramani, G. Kumarapandiyan
Department of Statistics, Ramanujan School of Mathematical Sciences, Pondicherry University, R V Nagar, Kalapet, Puducherry, 605014, India
Correspondence to: J. Subramani, Department of Statistics, Ramanujan School of Mathematical Sciences, Pondicherry University, R V Nagar, Kalapet, Puducherry, 605014, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In the past, a number of modified ratio estimators are suggested for estimation of the population mean of the study variable using Co-efficient of Variation, Co-efficient of Kurtosis, Co-efficient of Skewness, Population Correlation Coefficient, Median, Quartile and their linear combinations of the auxiliary variable. However no attempt is made to use the deciles, which are more generalized version of quartiles and Median. Hence an attempt is made in this paper to use the deciles in the modified ratio estimators for estimation of population mean of the study variable when the population deciles of the auxiliary variable are known. The biases and the mean squared errors of the proposed estimators are derived and are compared with that of existing modified ratio estimators for certain known populations. Further we have also derived the conditions for which the proposed estimators perform better than the existing modified ratio estimators. From the numerical study it is observed that the proposed modified ratio estimators perform better than the existing modified ratio estimators.
Keywords:
Bias, Mean Squared Error, Population Mean, Simple Random Sampling
Cite this paper:
J. Subramani, G. Kumarapandiyan, "A Class of Modified Ratio Estimators Using Deciles of an Auxiliary Variable", International Journal of Statistics and Applications, Vol. 2 No. 6, 2012, pp. 101-107. doi: 10.5923/j.statistics.20120206.02.
1. Introduction
Consider a finite population 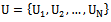 of
of 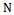 distinct and identifiable units. Let
distinct and identifiable units. Let 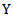 be a real variable with value
be a real variable with value 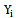 measured on
measured on 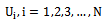 giving a vector
giving a vector 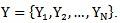 The problem is to estimate the population mean
The problem is to estimate the population mean 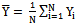 on the basis of a random sample selected from the population
on the basis of a random sample selected from the population 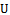 . If the population parameters of the auxiliary variable
. If the population parameters of the auxiliary variable 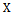 such as Population Mean, Co-efficient of Variation, Co-efficient of Kurtosis, Co-efficient of Skewness, Median, Quartiles etc., are known, a number of modified ratio estimators proposed in the literature. Before discussing further about the existing modified ratio estimators and the proposed modified ratio estimators the notations to be used in this paper are described below:
such as Population Mean, Co-efficient of Variation, Co-efficient of Kurtosis, Co-efficient of Skewness, Median, Quartiles etc., are known, a number of modified ratio estimators proposed in the literature. Before discussing further about the existing modified ratio estimators and the proposed modified ratio estimators the notations to be used in this paper are described below: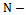 Population size
Population size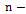 Sample size
Sample size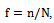 Sampling fraction
Sampling fraction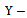 Study variable
Study variable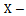 Auxiliary variable
Auxiliary variable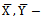 Population means-
Population means-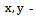 Sample totals
Sample totals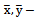 Sample means
Sample means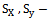 Population standard deviations
Population standard deviations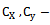 Coefficient of variations
Coefficient of variations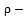 Coefficient of correlation
Coefficient of correlation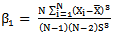 , Coefficient of skewness of the auxiliary variable
, Coefficient of skewness of the auxiliary variable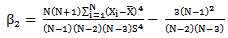 , Coefficient of kurtosis of the auxiliary variable
, Coefficient of kurtosis of the auxiliary variable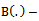 Bias of the estimator
Bias of the estimator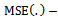 Mean squared error of the estimator
Mean squared error of the estimator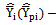 Existing (proposed) modified ratio estimator of
Existing (proposed) modified ratio estimator of 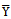 The Ratio estimator for estimating the population mean
The Ratio estimator for estimating the population mean 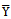 of the study variable
of the study variable 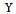 is defined as
is defined as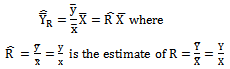 | (1) |
The Ratio estimator given in (1) is used for improving the precision of the estimate of the population mean compared to simple random sampling whenever a positive correlation exist between  and
and  . Further improvements are achieved by introducing a large number of modified ratio estimators with the use of known Co-efficient of Variation, Co-efficient of Kurtosis, Co-efficient of Skewness etc. A list of existing modified ratio estimators, which are to be compared with that of proposed estimators are given in Table 1 together with their biases, mean squared errors and constants.
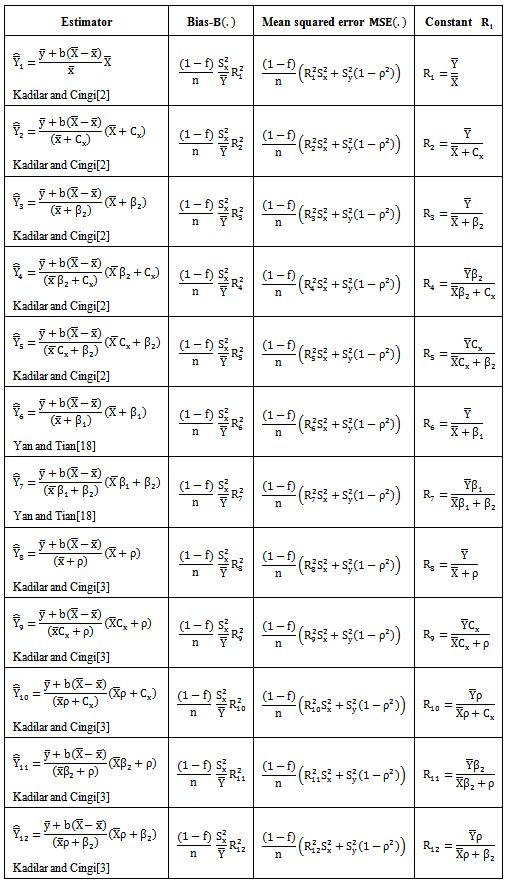
. Further improvements are achieved by introducing a large number of modified ratio estimators with the use of known Co-efficient of Variation, Co-efficient of Kurtosis, Co-efficient of Skewness etc. A list of existing modified ratio estimators, which are to be compared with that of proposed estimators are given in Table 1 together with their biases, mean squared errors and constants.Table 1. Existing modified ratio estimators with their biases, mean squared errors and their constants
 |
| |
|
It is to be noted that “the existing modified ratio estimators” means the list of modified ratio estimators to be considered in this paper unless otherwise stated. It does not mean to the entire list of modified ratio type estimators available in the literature. For a more detailed discussion on the ratio estimator and its modifications one may refer to Cochran[1], Kadilar and Cingi[2, 3], Koyuncu and Kadilar[4], Murthy[5], Prasad[6], Rao[7], Singh[9], Singh and Tailor[10, 12], Singh et.al[11], Sisodia and Dwivedi[13], Subramani and Kumarapandiyan[14, 15 and 16], Upadhyaya and Singh[17], Yan and Tian[18] and the references cited there in.The list of estimators given in Table 1 uses the known values of the parameters like 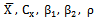 and their linear combinations. However, it seems, no attempt is made to use the known values of the population deciles of the auxiliary variable to improve the ratio estimator. Further we know that the parameters like the mean, coefficient of variation, coefficient of skewness and coefficient of kurtosis are affected by the extreme values or the presence of outliers in the population value, while deciles are unaffected and are robustness to extreme values. The points discussed above have motivated us to introduce a class of modified ratio estimators using the known value of the population deciles of the auxiliary variable and it is observed that the proposed estimators perform better than the existing estimators. The proposed modified ratio estimators using known values of population deciles of the auxiliary variable are presented in section 2 where as the conditions in which the proposed estimators perform better than the existing modified ratio estimators are derived in section 3. The efficiencies of the proposed modified ratio estimators and the existing modified ratio estimators are assessed for certain natural populations in section 4 whereas the conclusion part is presented in section 5.
and their linear combinations. However, it seems, no attempt is made to use the known values of the population deciles of the auxiliary variable to improve the ratio estimator. Further we know that the parameters like the mean, coefficient of variation, coefficient of skewness and coefficient of kurtosis are affected by the extreme values or the presence of outliers in the population value, while deciles are unaffected and are robustness to extreme values. The points discussed above have motivated us to introduce a class of modified ratio estimators using the known value of the population deciles of the auxiliary variable and it is observed that the proposed estimators perform better than the existing estimators. The proposed modified ratio estimators using known values of population deciles of the auxiliary variable are presented in section 2 where as the conditions in which the proposed estimators perform better than the existing modified ratio estimators are derived in section 3. The efficiencies of the proposed modified ratio estimators and the existing modified ratio estimators are assessed for certain natural populations in section 4 whereas the conclusion part is presented in section 5.
2. Proposed Modified Ratio Type Estimators
In this section, we have suggested a class of modified ratio type estimators using the population deciles, denoted by 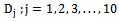 of the auxiliary variable. The proposed modified ratio type estimators
of the auxiliary variable. The proposed modified ratio type estimators 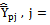
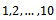 for estimating the population mean
for estimating the population mean 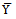 together with the first degree of approximation, the biases and mean squared errors and the constants are given below:
together with the first degree of approximation, the biases and mean squared errors and the constants are given below:Table 2. Proposed modified ratio estimators with their biases, mean squared errors and their constants
 |
| |
|
3. Efficiency of the Proposed Estimators
For want of space; for the sake of convenience to the readers and for the ease of comparisons, the modified ratio estimators given in Table 1and the proposed modified ratio estimators given in Table 2 are represented into two classes as given below: Class 1: The biases, the mean squared errors and the constants of the 12 modified ratio estimators 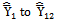 listed in the Table 1 are represented in a single class (say, Class 1), which will be very much useful for comparing with that of proposed modified ratio estimators and are given below:
listed in the Table 1 are represented in a single class (say, Class 1), which will be very much useful for comparing with that of proposed modified ratio estimators and are given below: | (2) |
Class 2:The biases, the mean squared errors and the constants of the 10 proposed modified ratio estimators 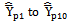 listed in the Table 2 are represented in a single class (say, Class 2), which will be very much useful for comparing with that of existing modified ratio estimators (given in Class1) are given below:
listed in the Table 2 are represented in a single class (say, Class 2), which will be very much useful for comparing with that of existing modified ratio estimators (given in Class1) are given below: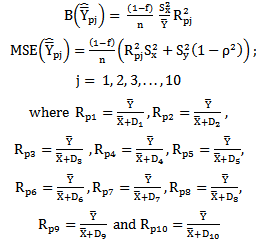 | (3) |
From the expressions given in (2) and (3) we have derived the conditions for which the proposed estimator 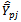 is more efficient than the existing modified ratio type estimators given in Class 1,
is more efficient than the existing modified ratio type estimators given in Class 1, 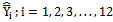 and are given below.
and are given below.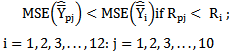 | (4) |
4. Empirical Study
The performances of the proposed modified ratio estimators listed in Table 2 are assessed with that of existing modified ratio estimators listed in Table 1 for certain natural populations. In this connection, we have considered three natural populations for the assessment of the performances of the proposed modified ratio estimators with that of existing modified ratio estimators. They are: The population 1 is the closing price of the industry ACC in the National Stock Exchange from 2, January 2012 to 27, February 2012[19]; population 2 and population 3 are taken from Singh and Chaudhary[8] given in page 177. The population parameters and the constants computed from the above populations are given below in Table 3, where as the constants, the biases and the mean squared errors of the existing and proposed modified ratio estimators for the above populations are respectively given from the Tables 4 to 6.Table 3. Parameters and Constants of the Populations
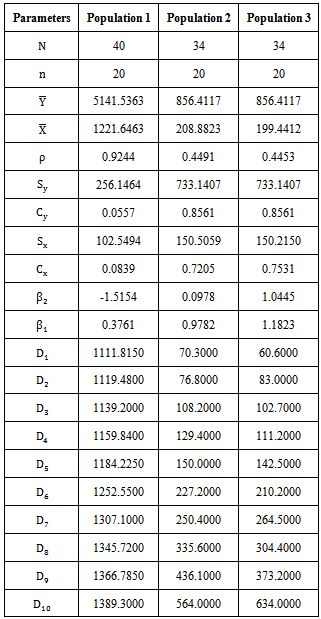 |
| |
|
Table 4. The constants of the existing and proposed modified ratio type estimators
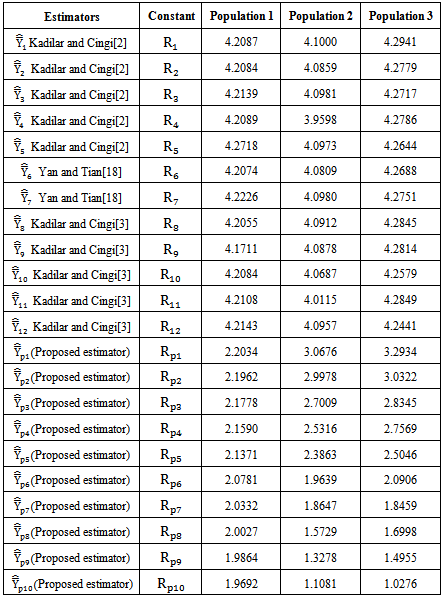 |
| |
|
Table 5. The biases of the existing and proposed modified ratio type estimators
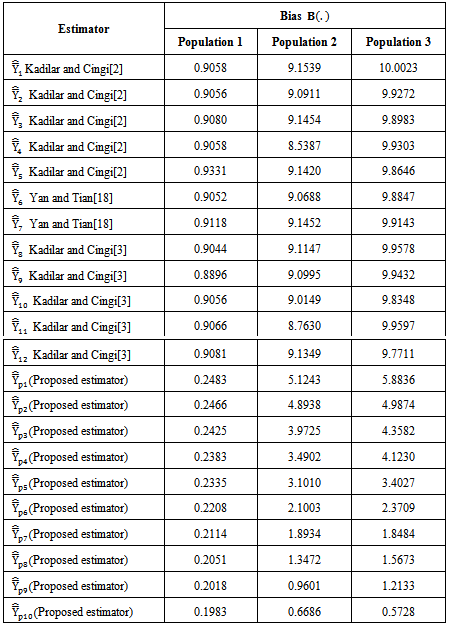 |
| |
|
Table 6. The mean squared errors of the existing and proposed modified ratio type estimators
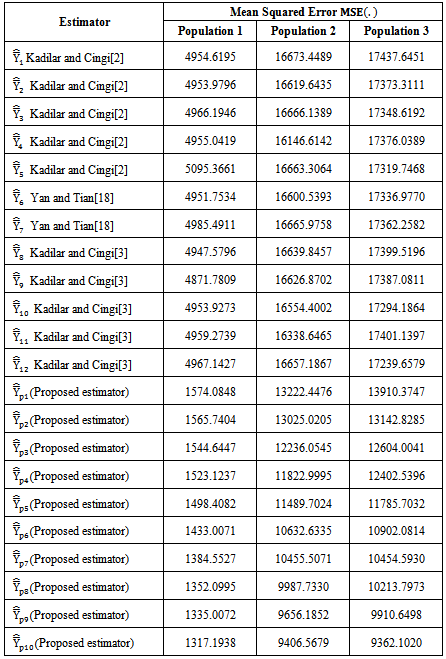 |
| |
|
From the values of Table 5, it is observed that the biases of the proposed modified ratio estimators are less than the biases of all the 12 existing modified ratio estimators. Similarly from the values of Table 6, it is observed that the mean squared errors of the proposed modified ratio estimators are less than the mean squared errors of all the 12 existing modified ratio estimators.
5. Conclusions
In this paper we have proposed a class of modified ratio type estimators using known values of population deciles of the auxiliary variable. The biases and mean squared errors of the proposed estimators are obtained and compared with that of existing modified ratio estimators. Further we have derived the conditions for which the proposed estimators are more efficient than the existing modified ratio estimators. We have also assessed the performances of the proposed estimators for some known populations given in page 177 of Singh and Chaudhary [8]. It is observed that the biases and mean squared errors of the ten proposed estimators based on the deciles are less than the biases and mean squared errors of the existing modified ratio estimators for all the three known populations considered for the numerical study. Hence we strongly recommend that the proposed modified estimators with use of deciles, particularly the higher order deciles may be preferred over the existing modified ratio estimators for the use of practical applications.
ACKNOWLEDGEMENTS
The authors record their gratitude to the editor and the reviewer for their constructive comments, which have improved the presentation of the paper; to the Vice Chancellor, Pondicherry University for having provided the necessary facilities to carry out this research work.
References
| [1] | Cochran, W. G. (1977): Sampling techniques, Third Edition, Wiley Eastern Limited |
| [2] | Kadilar, C. and Cingi, H. (2004): Ratio estimators in simple random sampling, Applied Mathematics and Computation 151, 893-902 |
| [3] | Kadilar, C. and Cingi, H. (2006): An Improvement in estimating the population mean by using the Correlation Coefficient, Hacettepe Journal of Mathematics and Statistics Volume 35 (1), 103-109 |
| [4] | Koyuncu, N. and Kadilar, C. (2009): Efficient estimators for the population mean, Hacettepe Journal of Mathematics and Statistics, Volume 38(2), 217-225 |
| [5] | Murthy, M.N. (1967): Sampling theory and methods, Statistical Publishing Society, Calcutta, India |
| [6] | Prasad, B. (1989): Some improved ratio type estimators of population mean and ratio in finite population sample surveys, Communications in Statistics: Theory and Methods 18, 379–392, |
| [7] | Rao, T.J. (1991): On certain methods of improving ratio and regression estimators, Communications in Statistics: Theory and Methods 20 (10), 3325–3340 |
| [8] | Singh, D. and Chaudhary, F.S. (1986): Theory and analysis of sample survey designs, New Age International Publisher |
| [9] | Singh, G.N. (2003): On the improvement of product method of estimation in sample surveys, Journal of the Indian Society of Agricultural Statistics 56 (3), 267–265 |
| [10] | Singh, H.P. and Tailor, R. (2003): Use of known correlation coefficient in estimating the finite population means, Statistics in Transition 6 (4), 555-560 |
| [11] | Singh, H.P., Tailor, R., Tailor, R. and Kakran, M.S. (2004): An improved estimator of population mean using power transformation, Journal of the Indian Society of Agricultural Statistics 58(2), 223-230 |
| [12] | Singh, H.P. and Tailor, R. (2005): Estimation of finite population mean with known coefficient of variation of an auxiliary, STATISTICA, anno LXV, n.3, pp 301-313 |
| [13] | Sisodia, B.V.S. and Dwivedi, V.K. (1981): A modified ratio estimator using coefficient of variation of auxiliary variable, Journal of the Indian Society of Agricultural Statistics 33(1), 13-18 |
| [14] | Subramani, J. and Kumarapandiyan, G. (2012): A class of almost unbiased modified ratio estimators for population mean with known population parameters, Elixir Statistics 44, 7411-7415 |
| [15] | Subramani, J. and Kumarapandiyan, G. (2012): Almost unbiased modified linear regression estimators for estimation of population mean, Bonfring International Journal of Industrial Engineering and Management Science, Vol. 2(2), 24-27 |
| [16] | Subramani, J. and Kumarapandiyan, G. (2012). Modified ratio estimators for population mean using function of quartiles of auxiliary variable, Bonfring International Journal of Industrial Engineering and Management Science, Vol. 2(2), 19-23 |
| [17] | Upadhyaya, L.N. and Singh, H.P. (1999): Use of transformed auxiliary variable in estimating the finite population mean, Biometrical Journal 41 (5), 627-636 |
| [18] | Yan, Z. and Tian, B. (2010): Ratio method to the mean estimation using coefficient of skewness of auxiliary variable, ICICA 2010, Part II, CCIS 106, pp. 103–110 |
| [19] | www.nseindia.com/index.htm, Historical Security-wise Price Volume Data- Data for ACC - EQ from 02-01-2012 to 27-02-2012 |

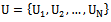 of
of 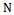 distinct and identifiable units. Let
distinct and identifiable units. Let 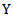 be a real variable with value
be a real variable with value 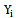 measured on
measured on 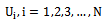 giving a vector
giving a vector 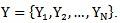 The problem is to estimate the population mean
The problem is to estimate the population mean 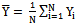 on the basis of a random sample selected from the population
on the basis of a random sample selected from the population 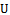 . If the population parameters of the auxiliary variable
. If the population parameters of the auxiliary variable 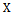 such as Population Mean, Co-efficient of Variation, Co-efficient of Kurtosis, Co-efficient of Skewness, Median, Quartiles etc., are known, a number of modified ratio estimators proposed in the literature. Before discussing further about the existing modified ratio estimators and the proposed modified ratio estimators the notations to be used in this paper are described below:
such as Population Mean, Co-efficient of Variation, Co-efficient of Kurtosis, Co-efficient of Skewness, Median, Quartiles etc., are known, a number of modified ratio estimators proposed in the literature. Before discussing further about the existing modified ratio estimators and the proposed modified ratio estimators the notations to be used in this paper are described below: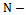 Population size
Population size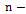 Sample size
Sample size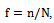 Sampling fraction
Sampling fraction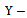 Study variable
Study variable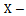 Auxiliary variable
Auxiliary variable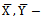 Population means-
Population means-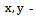 Sample totals
Sample totals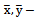 Sample means
Sample means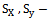 Population standard deviations
Population standard deviations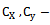 Coefficient of variations
Coefficient of variations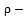 Coefficient of correlation
Coefficient of correlation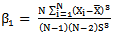 , Coefficient of skewness of the auxiliary variable
, Coefficient of skewness of the auxiliary variable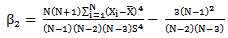 , Coefficient of kurtosis of the auxiliary variable
, Coefficient of kurtosis of the auxiliary variable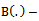 Bias of the estimator
Bias of the estimator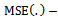 Mean squared error of the estimator
Mean squared error of the estimator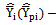 Existing (proposed) modified ratio estimator of
Existing (proposed) modified ratio estimator of 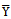 The Ratio estimator for estimating the population mean
The Ratio estimator for estimating the population mean 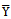 of the study variable
of the study variable 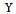 is defined as
is defined as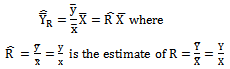
 and
and  . Further improvements are achieved by introducing a large number of modified ratio estimators with the use of known Co-efficient of Variation, Co-efficient of Kurtosis, Co-efficient of Skewness etc. A list of existing modified ratio estimators, which are to be compared with that of proposed estimators are given in Table 1 together with their biases, mean squared errors and constants.
. Further improvements are achieved by introducing a large number of modified ratio estimators with the use of known Co-efficient of Variation, Co-efficient of Kurtosis, Co-efficient of Skewness etc. A list of existing modified ratio estimators, which are to be compared with that of proposed estimators are given in Table 1 together with their biases, mean squared errors and constants. and their linear combinations. However, it seems, no attempt is made to use the known values of the population deciles of the auxiliary variable to improve the ratio estimator. Further we know that the parameters like the mean, coefficient of variation, coefficient of skewness and coefficient of kurtosis are affected by the extreme values or the presence of outliers in the population value, while deciles are unaffected and are robustness to extreme values. The points discussed above have motivated us to introduce a class of modified ratio estimators using the known value of the population deciles of the auxiliary variable and it is observed that the proposed estimators perform better than the existing estimators. The proposed modified ratio estimators using known values of population deciles of the auxiliary variable are presented in section 2 where as the conditions in which the proposed estimators perform better than the existing modified ratio estimators are derived in section 3. The efficiencies of the proposed modified ratio estimators and the existing modified ratio estimators are assessed for certain natural populations in section 4 whereas the conclusion part is presented in section 5.
and their linear combinations. However, it seems, no attempt is made to use the known values of the population deciles of the auxiliary variable to improve the ratio estimator. Further we know that the parameters like the mean, coefficient of variation, coefficient of skewness and coefficient of kurtosis are affected by the extreme values or the presence of outliers in the population value, while deciles are unaffected and are robustness to extreme values. The points discussed above have motivated us to introduce a class of modified ratio estimators using the known value of the population deciles of the auxiliary variable and it is observed that the proposed estimators perform better than the existing estimators. The proposed modified ratio estimators using known values of population deciles of the auxiliary variable are presented in section 2 where as the conditions in which the proposed estimators perform better than the existing modified ratio estimators are derived in section 3. The efficiencies of the proposed modified ratio estimators and the existing modified ratio estimators are assessed for certain natural populations in section 4 whereas the conclusion part is presented in section 5.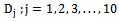 of the auxiliary variable. The proposed modified ratio type estimators
of the auxiliary variable. The proposed modified ratio type estimators 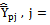
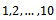 for estimating the population mean
for estimating the population mean 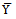 together with the first degree of approximation, the biases and mean squared errors and the constants are given below:
together with the first degree of approximation, the biases and mean squared errors and the constants are given below: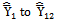 listed in the Table 1 are represented in a single class (say, Class 1), which will be very much useful for comparing with that of proposed modified ratio estimators and are given below:
listed in the Table 1 are represented in a single class (say, Class 1), which will be very much useful for comparing with that of proposed modified ratio estimators and are given below: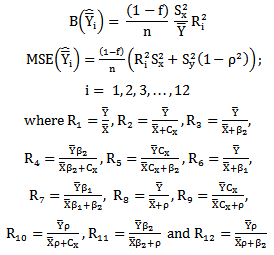
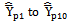 listed in the Table 2 are represented in a single class (say, Class 2), which will be very much useful for comparing with that of existing modified ratio estimators (given in Class1) are given below:
listed in the Table 2 are represented in a single class (say, Class 2), which will be very much useful for comparing with that of existing modified ratio estimators (given in Class1) are given below: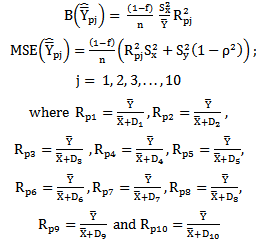
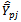 is more efficient than the existing modified ratio type estimators given in Class 1,
is more efficient than the existing modified ratio type estimators given in Class 1, 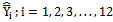 and are given below.
and are given below.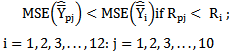
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML




