-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Statistics and Applications
p-ISSN: 2168-5193 e-ISSN: 2168-5215
2012; 2(5): 60-66
doi:10.5923/j.statistics.20120205.03
Weibull Geometric Process Model for the Analysis of Accelerated Life Testing with Complete Data
Mustafa Kamal, Shazia Zarrin, S. Saxena, Arif-Ul-Islam
Department of Statistics & Operations Research, Aligarh Muslim University, Aligarh, India
Correspondence to: Mustafa Kamal, Department of Statistics & Operations Research, Aligarh Muslim University, Aligarh, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper the Weibull geometric process model is utilized for the analysis of accelerated life testing under constant stress. By assuming that the lifetimes under increasing stress levels form a geometric process, the maximum likelihood estimates of the parameters and their confidence intervals (CIs) using both asymptotic and parametric bootstrap method are derived. The performance of the estimators is evaluated by a simulation study with different pre-fixed parameters. This paper also compares the geometric process model with the traditional log-linear model. A simulation study is also performed to compare the performances of the geometric model and the log-linear model.
Keywords: Maximum Likelihood Estimator, Fisher Information Matrix, Asymptotic Confidence Interval, Log Linear Modal, Bootstrap Confidence Interval, Simulation Study
Cite this paper: Mustafa Kamal, Shazia Zarrin, S. Saxena, Arif-Ul-Islam, Weibull Geometric Process Model for the Analysis of Accelerated Life Testing with Complete Data, International Journal of Statistics and Applications, Vol. 2 No. 5, 2012, pp. 60-66. doi: 10.5923/j.statistics.20120205.03.
Article Outline
1. Introduction
- In traditional life testing and reliability experiments, researchers used to analyze time-to-failure data obtained under normal operating conditions in order to quantify the product’s failure-time distribution and its associated parameters. However, such life data has become very difficult to obtain as a result of the great reliability of today’s products, and the small time period between design and release. This problem has motivated researchers to develop new life testing methods and obtain timely information on the reliability of product components and materials. Accelerated life testing (ALT) is then adopted and widely used in manufacturing industries. In such testing situations, products are tested at higher-than-usual levels of stress (e.g., temperature, voltage, humidity, vibration or pressure) to induce early failure. The life data collected from such accelerated tests is then analyzed and extrapolated to estimate the life characteristics under normal operating conditions. It is useful to divide accelerated tests into two aims (i) during product development, a small number of prototype specimens are forced to fail at high stress. Engineers examine the specimens to identify the causes of failure, and then determine how to improve the product to eliminate or reduce those causes. For thousands of years, engineers have improved product reliability with such development testing, called environmental stress screening (ESS) and HALT (highly accelerated life testing). Such testing depends on qualitative engineering knowledge of the product and usually does not involve a physical-statistical model. (ii) After product development, a statistical sample of specimens is tested at high stress levels to measure reliability, that is, to estimate the product life distribution or degradation at lower design stress levels. Such estimation requires a suitable model.Three types of stress loadings are usually applied in accelerated life tests: constant stress, step stress and linearly increasing stress. The constant stress loading, which is a time-independent test setting, has several advantages over the time-dependent stress loadings. For example, most products are assumed to operate at a constant stress under normal use. Therefore, a constant stress test mimics actual use. Besides, it is easier to run and to quantify a constant stress test. In the current study, we only discuss the application of constant stress in accelerated life testing.The log linear (LL) model with maximum likelihood (ML) method has been extensively studied in the literature. Evans[1] considered the exponential distribution in which the life characteristic is related to stress by the Arrhenius equation, which is a special case of the log-linear relationship. He derived the ML estimates of parameters at specified stress and used asymptotic theory to obtain the confidence limits. McCool[2] treated a 2-parameter Weibull distribution with the scale parameter a power function of stress. A numerical scheme was applied to solve the nonlinear simultaneous equations for the ML estimates of the shape parameter and the stress-life exponent. Watkins[3] discussed how to obtain ML estimates of parameters in a Weibull log-linear model and illustrated the numerical approach by two examples. More recently, Watkins[4] studied a variant of the basic Type II censoring scheme, and considered the statistical properties of maximum likelihood estimators of Weibull log-linear model under the certain design.Despite the popularity and wide application of the log linear model, researchers are still seeking development spaces for the statistical methods of accelerated life test. Watkins[5] argued that even though the log-linear function is just a simple reparameterization of the original parameter of the life distribution, from a statistical perspective, it is preferable to work with the original parameters. Inspired by Watkins, Balakrishnan et al[6], and Balakrishnan and Xie [7] considered the exponential lifetimes under the simple step-stress experiment terminated by Type-II censoring and Type-I hybrid censoring schemes, respectively. Both articles implemented the maximum likelihood method to directly estimate the scale parameter at each of the two stress levels instead of developing inferences for the parameters of the log-linear link function. Different types of confidence intervals are also derived and compared by simulation studies. These studies provide a new perspective of modeling the accelerated life data in which the MLEs of the unknown parameters of life distribution are derived directly, and construct their confidence intervals.The concept of geometric process (GP) is first introduced by Lam in 1988[8, 9] when he studied the problem of repair replacement. Lam[10] introduced least square and modified moment estimation of parameters for GP, and studied the asymptotic normal properties of these estimators. Lam and Chan[11] derived the maximum likelihood estimate of parameters of the GP with lognormal distribution. Chen[12] provided the Bayesian approach to the estimation of parameters in a GP with several popular life distributions including the exponential and lognormal distributions. Lam and Zhang[13] introduced the geometric process model in the analysis of a two-component series system with one repairman. Lam[14] studied the geometric process model for a multistate system and determined an optimal replacement policy to minimize the long run average cost per unit time. Zhang[15] used the geometrical process to model a simple repairable system with delayed repair. Large amount of studies in maintenance problems and system reliability have shown that a geometric process model is a good and simple model for analysis of data with a single trend or multiple trends. So far, only Huang [16] utilizes the geometric process in the analysis of accelerated life test with complete and censored exponential samples under the constant stress.In this paper, the geometric process model is extended for the analysis of accelerated life testing with Weibull life distribution under constant stress with complete data. Statistical inference of the parameters are made and examined through a simulation study. It is reasonable to believe that in an accelerated life testing, lifetimes of products are stochastically decreasing with respect to increasing stress levels. Therefore, the geometric process model is a natural approach to study such problems.
2. The Model
2.1. The Geometric Process
- A geometric process describes a stochastic process
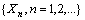 , where there exists a real valued
, where there exists a real valued 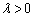 such that
such that 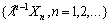 forms a renewal process. The positive number
forms a renewal process. The positive number 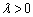 is called the ratio of the GP. It is clear to see that a GP is stochastically increasing if
is called the ratio of the GP. It is clear to see that a GP is stochastically increasing if 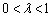 and stochastically decreasing if
and stochastically decreasing if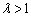 . Therefore, the GP is a natural approach to analyze data from a series of events with trend.It can be shown that if
. Therefore, the GP is a natural approach to analyze data from a series of events with trend.It can be shown that if 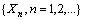 is a GP and the pdf of
is a GP and the pdf of 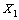 is
is 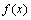 with mean
with mean 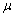 and variance
and variance 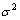 then the pdf of
then the pdf of 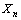 will be given be
will be given be 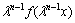 with
with 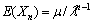 and
and 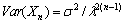 . Thus
. Thus 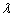
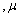 and
and 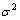 are three important parameters of a GP.
are three important parameters of a GP.2.2. The Weibull Distribution
- The probability density function (pdf) of a two parameter Weibull distribution is given by
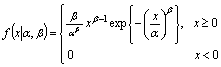 where
where 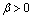 is the shape parameter and
is the shape parameter and 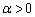 is the scale parameter of the distribution. The Weibull distribution is related to a number of other probability distributions; in particular, it interpolates between the exponential distribution for
is the scale parameter of the distribution. The Weibull distribution is related to a number of other probability distributions; in particular, it interpolates between the exponential distribution for 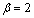 and the Rayleigh distribution
and the Rayleigh distribution 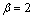 .The cumulative distribution function for the Weibull distribution is
.The cumulative distribution function for the Weibull distribution is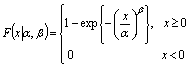 The survival function of the Weibull distribution takes the following form
The survival function of the Weibull distribution takes the following form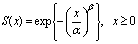 The failure rate (or hazard rate) for the Weibull distribution is given by
The failure rate (or hazard rate) for the Weibull distribution is given by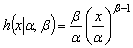 It is easy to verify that failure rate (or hazard rate) decreases over time if
It is easy to verify that failure rate (or hazard rate) decreases over time if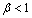 (or increases with time if
(or increases with time if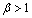 ) and
) and 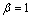 indicates that the failure rate is constant over time.
indicates that the failure rate is constant over time.2.3. Assumptions
- The geometric model for accelerated life test is based on the following assumptions:1. Suppose that an accelerated life test under
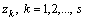 , arithmetically increasing stress levels is performed. A random sample of
, arithmetically increasing stress levels is performed. A random sample of 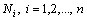 , identical items is placed under each stress level and start to operate at the same time. Whenever an item fails, it is removed from the test and it’s observed failure time
, identical items is placed under each stress level and start to operate at the same time. Whenever an item fails, it is removed from the test and it’s observed failure time 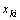 is recorded.2. At any constant stress level, the product lifetime has a two parameter Weibull.3. The Weibull shape parameter
is recorded.2. At any constant stress level, the product lifetime has a two parameter Weibull.3. The Weibull shape parameter 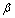 is constant, i.e. independent of stress.4. Let the sequence of random variables
is constant, i.e. independent of stress.4. Let the sequence of random variables 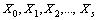 , denote the lifetimes under each stress level, where
, denote the lifetimes under each stress level, where 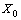 denotes item’s lifetime under the design stress. We assume
denotes item’s lifetime under the design stress. We assume 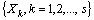 is a geometric process with ratio
is a geometric process with ratio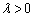 .Based on the definition given in subsection 2.1, if density function of
.Based on the definition given in subsection 2.1, if density function of 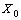 is
is 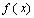 , then the probability density function of
, then the probability density function of 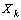 will be given by
will be given by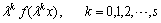 Therefore the pdf of a product lifetime at the
Therefore the pdf of a product lifetime at the  stress level is
stress level is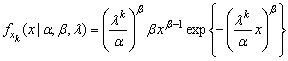 | (1) |
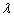 and if the life distribution at design stress level is Weibull with life characteristic
and if the life distribution at design stress level is Weibull with life characteristic 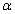 , then the life distribution at
, then the life distribution at 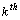 stress level is also Weibull with life characteristic
stress level is also Weibull with life characteristic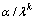 .
.2.4. Maximum likelihood Estimation
- The likelihood function for the Weibull geometric process model based on the observed data in a total stress levels in accelerated life testing, can be written as
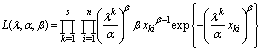 | (2) |
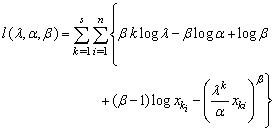 | (3) |
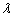 and
and 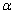 are:
are: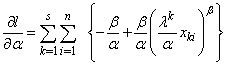 | (4) |
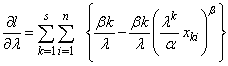 | (5) |
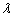 and
and 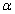 can be obtained by solving
can be obtained by solving 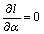 and
and 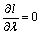 for
for 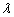 and
and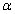 . As it seems that The MLEs of
. As it seems that The MLEs of 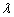 and
and  exist but do not have closed forms. Therefore, a numerical technique method, such as Newton-Rasphson method, must be used to obtain the MLEs.
exist but do not have closed forms. Therefore, a numerical technique method, such as Newton-Rasphson method, must be used to obtain the MLEs.3. Asymptotic Confidence Interval
- Let
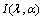 denotes the Fisher Information matrix, then observed Information matrix of
denotes the Fisher Information matrix, then observed Information matrix of 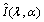 is given as
is given as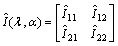 where
where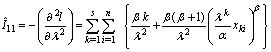
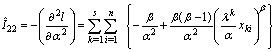
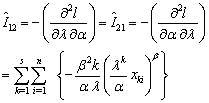 Now, the variance covariance matrix can be written as
Now, the variance covariance matrix can be written as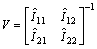
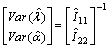 The
The 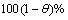 asymptotic confidence interval for
asymptotic confidence interval for 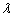 and
and 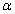 are then given respectively as
are then given respectively as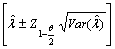 and
and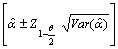
4. Bootstrap Confidence Interval
- We construct the confidence intervals for
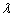 and
and 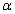 based on the parametric bootstrap, using the percentile bootstrap interval method. We describe the algorithm to obtain the coverage for bootstrap CI as below.1. Obtain
based on the parametric bootstrap, using the percentile bootstrap interval method. We describe the algorithm to obtain the coverage for bootstrap CI as below.1. Obtain 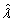 and
and 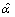 , the MLEs of
, the MLEs of 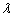 and
and 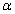 from (5) and (4) based on the original sample
from (5) and (4) based on the original sample 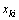 by using Newton iterative method.2. For
by using Newton iterative method.2. For 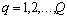 , simulate a bootstrap sample
, simulate a bootstrap sample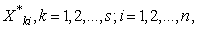 where
where 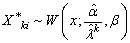 based onand.3. Compute
based onand.3. Compute 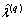 and
and 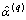 , the MLEs of and from (5) and (4) based on the simulated bootstrap by using Newton iterative method.4. Obtain
, the MLEs of and from (5) and (4) based on the simulated bootstrap by using Newton iterative method.4. Obtain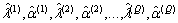 by repeating steps 2-3 for
by repeating steps 2-3 for 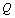 times.5. The bootstrap percentile confidence interval end points for
times.5. The bootstrap percentile confidence interval end points for 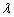 and
and 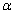 are the
are the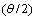 and
and 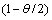 quantiles of
quantiles of 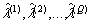 and
and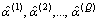 respectively.
respectively.5. Comparison of the Proposed Model with Log-Linear Model
- According to Nelson [17], the life characteristic
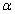 of the product at any constant stress level
of the product at any constant stress level 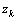 , is a log linear function of the stress:
, is a log linear function of the stress: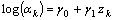 | (6) |
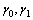 are unknown parameters that depend on the nature of the product under test. When
are unknown parameters that depend on the nature of the product under test. When 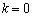 , the equation (6) depicts the relationship of life characteristic at designed stress level. It can easily be shown that
, the equation (6) depicts the relationship of life characteristic at designed stress level. It can easily be shown that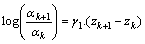 | (7) |
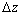 , the life characteristic under each stress level forms a geometric sequence with the ratio
, the life characteristic under each stress level forms a geometric sequence with the ratio 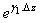 . That is,
. That is, 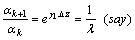 | (8) |
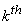 stress level is
stress level is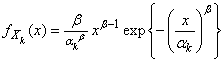 | (9) |
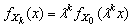 | (10) |
6. Simulation Study
- To evaluate and compare the performance of the methods of inference described in present model, first generate a random sample
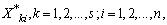 where
where 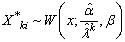 . The values of the parameters
. The values of the parameters 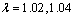 ,
, 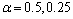 and
and 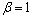 are chosen. The values of
are chosen. The values of 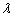 are chosen close to
are chosen close to 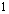 since the decreasing trend of lifetimes in practice is usually not pronounced. The number of stress levels are chosen to be
since the decreasing trend of lifetimes in practice is usually not pronounced. The number of stress levels are chosen to be 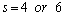 the number of test products at each stress level is
the number of test products at each stress level is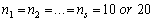 . The estimators and the corresponding summary statistics are obtained by our proposed model and the Newton iteration method. For a given sample with different choices of
. The estimators and the corresponding summary statistics are obtained by our proposed model and the Newton iteration method. For a given sample with different choices of 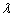 and
and 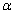 , the average of the ML estimations (mean), the sample standard deviation of the estimates
, the average of the ML estimations (mean), the sample standard deviation of the estimates 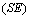 the average of asymptotic standard error
the average of asymptotic standard error 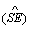 , the square root of mean squared error
, the square root of mean squared error 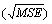 and the coverage rate of the 95% confidence interval for
and the coverage rate of the 95% confidence interval for 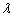 and
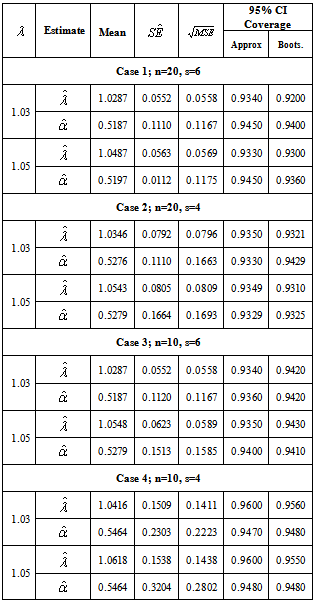
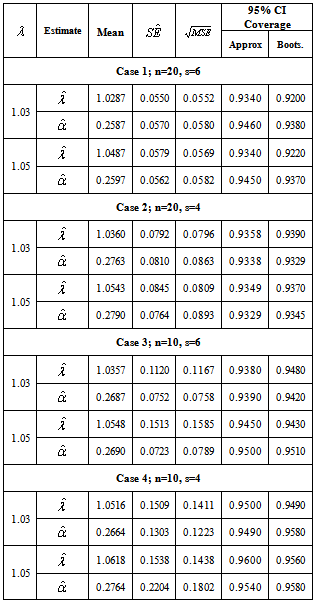
and 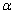 are obtained. The CIs are obtained by two methods: the asymptotic distribution and the parametric bootstrap. Table-1 and 2 summarize the results of the estimates for
are obtained. The CIs are obtained by two methods: the asymptotic distribution and the parametric bootstrap. Table-1 and 2 summarize the results of the estimates for 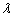 and
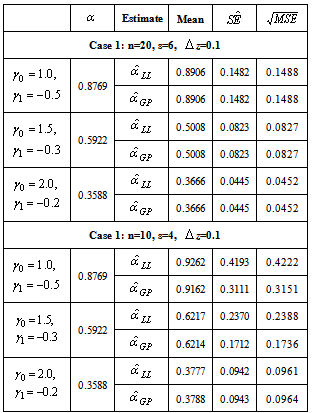
and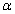 . The numerical results presented in Table-1 and 2 are based on 750 simulations and 750 bootstrap replications.Now to compare the estimation performances geometric process and log linear model, choose the first stress level
. The numerical results presented in Table-1 and 2 are based on 750 simulations and 750 bootstrap replications.Now to compare the estimation performances geometric process and log linear model, choose the first stress level 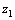 to be
to be 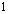 and the difference between each ascending stress level
and the difference between each ascending stress level 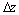 to be
to be 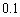 . Consequently, the normal stress level would be
. Consequently, the normal stress level would be 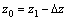 . Three pairs of parameters
. Three pairs of parameters 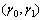 are chosen
are chosen 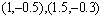 and
and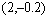 on the basis of the Xiong’s[18] simulation study. With the prefixed parameters
on the basis of the Xiong’s[18] simulation study. With the prefixed parameters 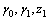 and
and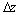 , the distribution parameter
, the distribution parameter 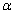 could be easily obtained by
could be easily obtained by 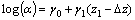 . For known values of
. For known values of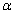 together with
together with 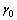 and
and 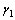 , the estimates of
, the estimates of 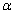 , the asymptotic standard error
, the asymptotic standard error 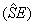 of
of 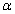 , and the square root of mean squared error
, and the square root of mean squared error  , are obtained by both geometric process and log linear model. The numerical results are based on 750 replications and presented in Table-3.
, are obtained by both geometric process and log linear model. The numerical results are based on 750 replications and presented in Table-3.
|
|
|
7. Conclusions
- From results in Table 1 and 2, it is observed that
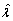 and
and 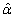 estimate the true parameters
estimate the true parameters 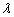 and
and 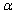 quite well respectively with relatively small mean squared errors. The estimated standard error also approximates well the sample standard deviation of the 750 estimates. For a fixed
quite well respectively with relatively small mean squared errors. The estimated standard error also approximates well the sample standard deviation of the 750 estimates. For a fixed 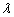 and
and 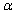 we compare their estimates across the four different cases and find that as
we compare their estimates across the four different cases and find that as 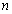 and
and 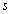 decreases, the mean squared errors of
decreases, the mean squared errors of 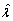 and
and 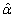 get larger. This may be because that a larger sample size results in a better large sample approximation for the distribution of
get larger. This may be because that a larger sample size results in a better large sample approximation for the distribution of 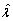 and
and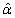 , so the inference for the parameters is more precise. It is also noticed that the coverage probabilities of the asymptotic confidence interval are close to the nominal level and do not change much across the four cases. The parametric bootstrap confidence intervals have similar coverage rates as the asymptotic CIs.The results in Table 3 indicate that most of the estimates from the geometric process model match the values obtained by the log linear model. It is seen that when the sample size and number of stress levels are relatively small, some of the estimates obtained by geometric process model have a smaller mean square error than that obtained by the log linear model. It is also noted that some estimates obtained by geometric process have a greater mean square error, but those differences are relatively very slight.In summary, the proposed geometric process model has a promising potential in the analysis of accelerated life testing when the stress increases arithmetically. It depicts the decreasing trend of lifetimes over increasing stress levels in an intuitive way and provides a simple form to derive the estimates of parameters at normal stress level. Therefore, it is reasonable to say that the proposed model works well.
, so the inference for the parameters is more precise. It is also noticed that the coverage probabilities of the asymptotic confidence interval are close to the nominal level and do not change much across the four cases. The parametric bootstrap confidence intervals have similar coverage rates as the asymptotic CIs.The results in Table 3 indicate that most of the estimates from the geometric process model match the values obtained by the log linear model. It is seen that when the sample size and number of stress levels are relatively small, some of the estimates obtained by geometric process model have a smaller mean square error than that obtained by the log linear model. It is also noted that some estimates obtained by geometric process have a greater mean square error, but those differences are relatively very slight.In summary, the proposed geometric process model has a promising potential in the analysis of accelerated life testing when the stress increases arithmetically. It depicts the decreasing trend of lifetimes over increasing stress levels in an intuitive way and provides a simple form to derive the estimates of parameters at normal stress level. Therefore, it is reasonable to say that the proposed model works well.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML