A. O. Adejumo , O. O. M. Sanni , E. T. Jolayemi , R. O. Ogedengbe
Department of Statistics University of Ilorin, Ilorin, Nigeria
Correspondence to: A. O. Adejumo , Department of Statistics University of Ilorin, Ilorin, Nigeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
s In some categorical tables, one of the classifying variables may be at least ordinal (ranked) arising from a follow-up or any similar study. The other classifying variable(s) may be that which separates the population into groups using variables such as gender, race or location, or a combination of some of them. The counts obtained this way are analyzed recognizing that one of the variables is nearly metric and must be used and interpretation becomes easier when appropriate model is fitted to the arising product multinomial. An example of such an approach is provided using the data from Tuberculosis Management in a Teaching Hospital. We observed that the recovery rate of females was faster than their males counterpart on the assumption that those discharged through management system follows an exponential distribution.
Keywords:
Panel data, Categorical data, Multinomial
Cite this paper:
A. O. Adejumo , O. O. M. Sanni , E. T. Jolayemi , R. O. Ogedengbe , "Analysis of Categorical Panel Data", International Journal of Statistics and Applications, Vol. 2 No. 5, 2012, pp. 56-59. doi: 10.5923/j.statistics.20120205.02.
1. Introduction
Categorical data are obtained when the variables which are discrete in nature are cross-classified and subjects having the same levels of the cross-classification are aggregated to form counts. Clearly such variables are at most ordinal in nature. Variables that are purely metric are reduced appropriately for categorical data analysis to be effected. In a follow-up (longitudinal) study the progression of positive outcome is critical and should be examined.Cross-classified data can have any of full-multinomial, hypergeometric, independent Poisson or product multinomial distributions, Bishop, Feinberg and Holland[1], Agresti[2], Sanni and Jolayemi[3], Adejumo[4] among many authors. All these distributions have fixed, but unknown, parameters. Each underlying distribution is dictated by the sampling scheme, even though the parameter estimates within each are identical as demonstrated by Birch[5], see also Jolayemi et al[6]. It is possible, however, that the parameters involved in the categorical data, have a specific pattern, especially when one or more of the categorical variables are metric but of constant interval. A statistical analysis approach for such data may be appropriate to use some models for probability outcomes. The model used, if appropriate can then be used to determine termination of management. This approach is in focus in this work.In this research, the main objective is to examine a model fitting-algorithm for a longitudinal categorical data. The follow-up data of this form becomes a panel data if the period for reassessment is constant.
2. Methodology
Consider an r x c contingency table. The row (r) categories are the sup-populations to be compared and column (c) equals the number of possible follow-ups. Let the matrix of observation be represented by 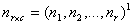 ,where
,where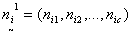 | (1) |
Within the foregoing, assume the product multinomial distribution for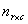 . Thus
. Thus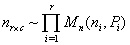 | (2) |
where 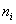 is as represented in 1.1,
is as represented in 1.1,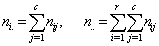 and
and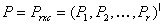 such that
such that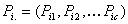 and
and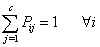 | (3) |
Furthermore, assume that for each i, the vector Pi has a known or suspected pattern 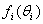 . The mixture model is with a compelling assumption if each
. The mixture model is with a compelling assumption if each 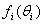 is unique, see for example Brooks et al.[7], when the variable characterizing the column is ordinal.The main aim of this study is to test some hypothesis regarding
is unique, see for example Brooks et al.[7], when the variable characterizing the column is ordinal.The main aim of this study is to test some hypothesis regarding 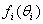 . In particular, we assume that
. In particular, we assume that  is exponential in this research paper with parameters
is exponential in this research paper with parameters 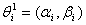 In this formulation,
In this formulation, 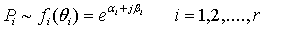 | (4) |
where j=1,2, …, c; indicating the outcome of the column variable. If βi < 0, the probability reduces over j (usually indexing time) or over jth follow-up time of constant period. What may be of interest here are various hypotheses regarding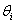 . Some of these include.(i)
. Some of these include.(i) 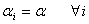 which represents all r rows are identical before follow-up(ii)
which represents all r rows are identical before follow-up(ii) 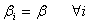 which can be interpreted to be identical reactions of the r subpopulation for the intervention of the follow-up.(iii)
which can be interpreted to be identical reactions of the r subpopulation for the intervention of the follow-up.(iii) 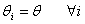 is the combination of (i) and (ii) above.Note that other forms of
is the combination of (i) and (ii) above.Note that other forms of 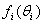 are possible. Such other forms includes
are possible. Such other forms includes 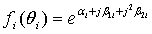 which is essentially used when the response is quadratic. It is also used for studying medical intervention.Let
which is essentially used when the response is quadratic. It is also used for studying medical intervention.Let 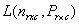 be the likelihood function for
be the likelihood function for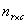 . Then,
. Then, 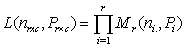
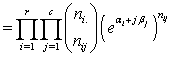 so that the log likelihood L under the constraint in equation (1) is given by
so that the log likelihood L under the constraint in equation (1) is given by 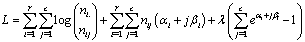 | (5) |
where λ is the Langrange multiplier (indicating the boundary limit). Clearly the log likelihood of equation (5) does not give normal equations which are linear in the parameters, see McCulagh and Nelder[8], Jolayemi and Okoro[9] for example.Let 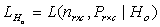 be the likelihood function using estimation
be the likelihood function using estimation 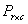 under the null hypothesis and
under the null hypothesis and 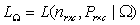 be the similar likelihood under the parameter space. The Likelihood ratio test statistic can be obtained from
be the similar likelihood under the parameter space. The Likelihood ratio test statistic can be obtained from 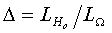 Under some regularity conditions, see Bickel et al.[10] and Adejumo[4],
Under some regularity conditions, see Bickel et al.[10] and Adejumo[4], 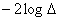 has the chi-square distribution with (k-m) degrees of freedom, where k and m are the number of parameters estimated under Ω and Ho respectively.
has the chi-square distribution with (k-m) degrees of freedom, where k and m are the number of parameters estimated under Ω and Ho respectively.
2.1. Estimation of Parameters
First consider the log likelihood function of equation (5) and let the null hypothesis Ho be given by 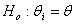 This is equivalent to
This is equivalent to 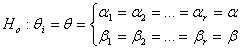 which represents gender insensitivity. Other forms of Ho can be used.The likelihood function LHo is given by
which represents gender insensitivity. Other forms of Ho can be used.The likelihood function LHo is given by 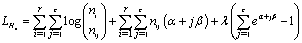 | (6) |
The normal equations from equation (6) are obtained as follows: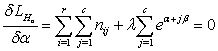 | (7) |
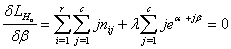 | (8) |
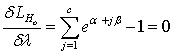 | (9) |
From equation (7) it is clear that λ = -n..Thus equations (7) and (8) become respectively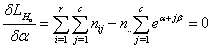 | (10) |
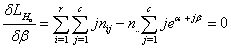 | (11) |
Let S2x1 represent the vector of normal equations.Then S is given bySo that the Hessian matrix, Morisson[11] is given by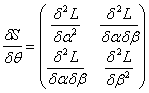 | (12) |
Let 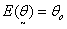 , then by mid-value theorem: Mood et al.[12]
, then by mid-value theorem: Mood et al.[12] 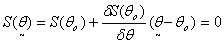 | (13) |
so that the 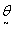 can be obtained as
can be obtained as 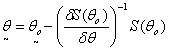 An iterative procedure is then used to obtain an estimate
An iterative procedure is then used to obtain an estimate 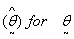 using an initial vector
using an initial vector 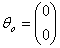 and tolerance
and tolerance 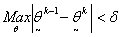 | (14) |
It is easy to note that the vector 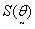 is given byAnd the cell values of the Hessian matrix is given by
is given byAnd the cell values of the Hessian matrix is given by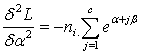
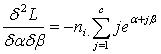
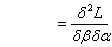
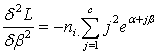 Under Ω, the above procedure is obtained for each i.Thus
Under Ω, the above procedure is obtained for each i.Thus 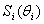 Finally, the estimate
Finally, the estimate 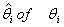 is obtained as explained earlier. The test statistic in this case which is the likelihood ratio test statistic is given by
is obtained as explained earlier. The test statistic in this case which is the likelihood ratio test statistic is given by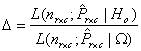 So that
So that 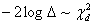 where d = (k - m) degrees of freedom. (k - m) = (2r - 2)=2(r - 1).If
where d = (k - m) degrees of freedom. (k - m) = (2r - 2)=2(r - 1).If 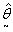 under Ho is given as
under Ho is given as 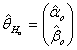 And
And 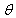 under Ω is given as
under Ω is given as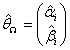 Then
Then 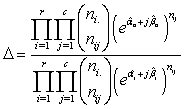
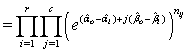
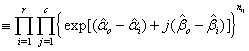 And -2log∆ is given as
And -2log∆ is given as 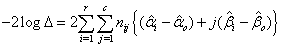 The above is a demonstration of how to produce software to perform the process for execution.
The above is a demonstration of how to produce software to perform the process for execution.
3. Empirical Results, Discussions and Conclusions
The method of application of mixture models for the 2-dimensional categorical data is demonstrated using a data set from a disease management from a hospital, the University of Ilorin Teaching Hospital (UITH), Nigeria, spanning the period between 1996 and 1998 on the management of Tuberculosis patients. The data excluded those who were lost to follow-up, so that, those who were successfully discharged were considered in Table 1 using approximated periods.| Table 1. 109 Tuberculosis patients classified by length of treatment and gender using one month follow up interval |
| | Duration (in month) | 1 | 2 | 3 | 4 | 5 | 6 | Total | | No. of Male | 44 | 17 | 6 | 3 | 3 | 1 | 74 | | No. of Female | 22 | 8 | 4 | 1 | 0 | 0 | 35 | | Total | 66 | 25 | 10 | 4 | 3 | 1 | 109 |
|
|
The analysis of the data followed equation (2) and the imposed models in equation (4). Using the tolerance limit δ = 0.001 for maximum difference in the parameter estimates as dictated by 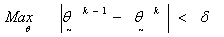 of equation (13), the following estimates were obtained:
of equation (13), the following estimates were obtained: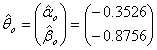
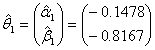
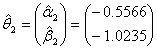 The likelihood ratio test statistic for
The likelihood ratio test statistic for 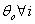 of G2=-2log∆=15.24 with d=2 degrees of freedom with p-value of 0.001 provided a bad fit This implies that a uniform distribution cannot be used for both males and females. Consequently, different models existed for males and females which were θ1 and θ2. This showed that the period of treatment was gender sensitive. While males would be treated for seven months the female counterpart would be treated for 4 months.
of G2=-2log∆=15.24 with d=2 degrees of freedom with p-value of 0.001 provided a bad fit This implies that a uniform distribution cannot be used for both males and females. Consequently, different models existed for males and females which were θ1 and θ2. This showed that the period of treatment was gender sensitive. While males would be treated for seven months the female counterpart would be treated for 4 months.
References
| [1] | Bishop, Y. M. M, Feinberg, S. E. Holland, P. W. (1975). Discrete Multivariate Analysis. Cambridge MA; MIT Press. |
| [2] | Agresti, A. (2002). Categorical Data Analysis. John Wiley and Sons. 2nd Edition. New York. |
| [3] | Sanni, O. O. M. and Jolayemi, E. T. (1998). On the use of some Categorical Test Statistic on Sparse Contingency Table. Journal of Pure and Applied Science. 509 – 514. |
| [4] | Adejumo, A. O (2005). Modelling Generalized Linear (Loglinear) Models for Raters Agreement measures; Peter Lang, Frankfurt am Main. (http://www.peterlang.de) |
| [5] | Birch, M. W. (1966). Maximum Likelihood in Three Way contingency Table. J. Royal Statistics Society, Series B25, 220 – 233. |
| [6] | Jolayemi, E. T. and Brown, M. B. (1984). The Choice of a log-linear model using Cp-type Statistics. Computational Statistics and Data Analysis. |
| [7] | Brooks, S. P, Morgan, B. J. T, Riobut, M. S, and Peak, S.C. (1997). Finite Mixture Models for Proportions. Biometric, 53; 1097 – 1115. |
| [8] | McCullagh, P. and Nelder, J. A. (1989). Generalised Linear Models. Chapman and Hall. New York. |
| [9] | Jolayemi, E. T. and Okoro, E. O (1995). On the estimation of mean IC50. Biosciences Research Communication, 7, 175 – 178. |
| [10] | Bickel, P. J. and Doksum, J. A. (1973). Mathematical Statistics. Holden Day, San Francisco. |
| [11] | Morrison, D. (1976). Multivariate Statistics Methods. McGraw Hill, New York. |
| [12] | Mood, A. M., Graybill, F. A., and Boes, D. C. (1963). Introduction to the Theory of Statistics. McGraw Hill, New York. |

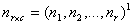 ,where
,where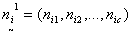
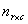 . Thus
. Thus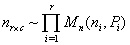
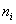 is as represented in 1.1,
is as represented in 1.1,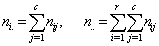 and
and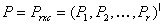 such that
such that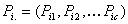 and
and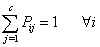
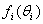 . The mixture model is with a compelling assumption if each
. The mixture model is with a compelling assumption if each 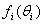 is unique, see for example Brooks et al.[7], when the variable characterizing the column is ordinal.The main aim of this study is to test some hypothesis regarding
is unique, see for example Brooks et al.[7], when the variable characterizing the column is ordinal.The main aim of this study is to test some hypothesis regarding 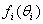 . In particular, we assume that
. In particular, we assume that  is exponential in this research paper with parameters
is exponential in this research paper with parameters 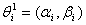 In this formulation,
In this formulation, 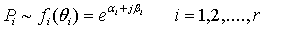
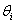 . Some of these include.(i)
. Some of these include.(i) 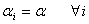 which represents all r rows are identical before follow-up(ii)
which represents all r rows are identical before follow-up(ii) 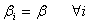 which can be interpreted to be identical reactions of the r subpopulation for the intervention of the follow-up.(iii)
which can be interpreted to be identical reactions of the r subpopulation for the intervention of the follow-up.(iii) 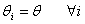 is the combination of (i) and (ii) above.Note that other forms of
is the combination of (i) and (ii) above.Note that other forms of 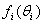 are possible. Such other forms includes
are possible. Such other forms includes 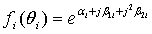 which is essentially used when the response is quadratic. It is also used for studying medical intervention.Let
which is essentially used when the response is quadratic. It is also used for studying medical intervention.Let 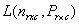 be the likelihood function for
be the likelihood function for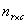 . Then,
. Then, 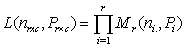
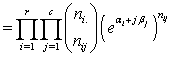 so that the log likelihood L under the constraint in equation (1) is given by
so that the log likelihood L under the constraint in equation (1) is given by 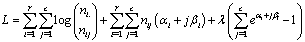
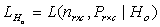 be the likelihood function using estimation
be the likelihood function using estimation 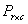 under the null hypothesis and
under the null hypothesis and 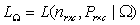 be the similar likelihood under the parameter space. The Likelihood ratio test statistic can be obtained from
be the similar likelihood under the parameter space. The Likelihood ratio test statistic can be obtained from 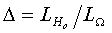 Under some regularity conditions, see Bickel et al.[10] and Adejumo[4],
Under some regularity conditions, see Bickel et al.[10] and Adejumo[4], 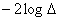 has the chi-square distribution with (k-m) degrees of freedom, where k and m are the number of parameters estimated under Ω and Ho respectively.
has the chi-square distribution with (k-m) degrees of freedom, where k and m are the number of parameters estimated under Ω and Ho respectively.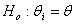 This is equivalent to
This is equivalent to 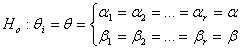 which represents gender insensitivity. Other forms of Ho can be used.The likelihood function LHo is given by
which represents gender insensitivity. Other forms of Ho can be used.The likelihood function LHo is given by 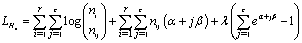
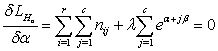
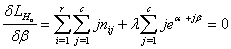
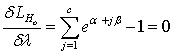
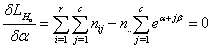
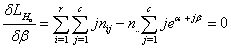
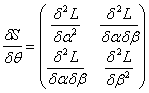
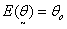 , then by mid-value theorem: Mood et al.[12]
, then by mid-value theorem: Mood et al.[12] 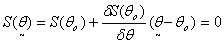
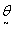 can be obtained as
can be obtained as 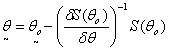 An iterative procedure is then used to obtain an estimate
An iterative procedure is then used to obtain an estimate 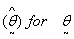 using an initial vector
using an initial vector 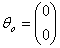 and tolerance
and tolerance 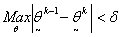
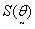 is given byAnd the cell values of the Hessian matrix is given by
is given byAnd the cell values of the Hessian matrix is given by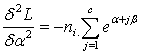
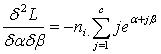
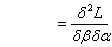
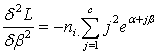 Under Ω, the above procedure is obtained for each i.Thus
Under Ω, the above procedure is obtained for each i.Thus  Finally, the estimate
Finally, the estimate 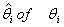 is obtained as explained earlier. The test statistic in this case which is the likelihood ratio test statistic is given by
is obtained as explained earlier. The test statistic in this case which is the likelihood ratio test statistic is given by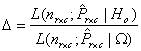 So that
So that 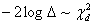 where d = (k - m) degrees of freedom. (k - m) = (2r - 2)=2(r - 1).If
where d = (k - m) degrees of freedom. (k - m) = (2r - 2)=2(r - 1).If 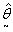 under Ho is given as
under Ho is given as 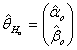 And
And 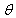 under Ω is given as
under Ω is given as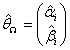 Then
Then 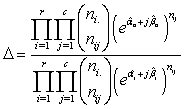
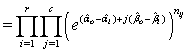
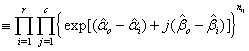 And -2log∆ is given as
And -2log∆ is given as 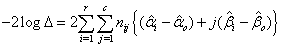 The above is a demonstration of how to produce software to perform the process for execution.
The above is a demonstration of how to produce software to perform the process for execution.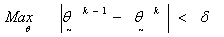 of equation (13), the following estimates were obtained:
of equation (13), the following estimates were obtained: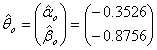
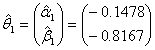
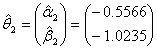 The likelihood ratio test statistic for
The likelihood ratio test statistic for 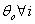 of G2=-2log∆=15.24 with d=2 degrees of freedom with p-value of 0.001 provided a bad fit This implies that a uniform distribution cannot be used for both males and females. Consequently, different models existed for males and females which were θ1 and θ2. This showed that the period of treatment was gender sensitive. While males would be treated for seven months the female counterpart would be treated for 4 months.
of G2=-2log∆=15.24 with d=2 degrees of freedom with p-value of 0.001 provided a bad fit This implies that a uniform distribution cannot be used for both males and females. Consequently, different models existed for males and females which were θ1 and θ2. This showed that the period of treatment was gender sensitive. While males would be treated for seven months the female counterpart would be treated for 4 months. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML