-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Statistics and Applications
2012; 2(4): 24-32
doi: 10.5923/j.statistics.20120204.01
Clustering Algorithms for Categorical Data: A Monte Carlo Study
Sueli A. Mingoti , Renata A. Matos
Department of Statistics, Federal University of Minas Gerais, Belo Horizonte, 31270-901, Brazil
Correspondence to: Sueli A. Mingoti , Department of Statistics, Federal University of Minas Gerais, Belo Horizonte, 31270-901, Brazil.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper the clustering algorithms: average linkage, ROCK, k-modes, fuzzy k-modes and k-populations were compared by means of Monte Carlo simulation. Data were simulated from Beta and Uniform distributions considering factors such as clusters overlapping, number of groups, variables and categories. A total of 64 population structures of clusters were simulated considering smaller and higher degree of overlapping, number of clusters, variables and categories. The results showed that overlapping was the factor with major impact in the algorithm’s accuracy which decreases as the number of clusters increases. In general, ROCK presented the best performance considering overlapping and non-overlapping cases followed by k-modes and fuzzy k-Modes. The k-populations algorithm showed better accuracy only in cases where there was a small degree of overlapping with performance similar to the average linkage. The superiority of k-populations algorithm over k-modes and fuzzy k-modes presented in previous studies, which were based only in benchmark data, was not confirmed in this simulation study.
Keywords: Clustering, Categorical Data, Monte Carlo Simulation
Article Outline
1. Introduction
- Clustering algorithms have been used in a variety of fields such as chemistry, engineering, medicine, etc.[2]. Given a data set the main goal is to produce a partition with high internal intra-class similarity and high inter-cluster dissimilarity. The majority of papers available in the literature deals with clustering algorithms for numerical data even though categorical data are very common in practical applications. Two well-known non-hierarchical algorithms to cluster categorical data are k-modes[20] and fuzzy k-modes[19], which are direct extensions of the k-means[26] and fuzzy c-means[23], respectively. Some alternative algorithms have been developed to increase the accuracy of k-modes and its efficiency to handle larger data sets. Some of these algorithms are direct variations of the k-modes or fuzzy k-modes (see[4] and[5], for examples). The variations include changing the dissimilarity measure used to compare the objects to the cluster centroids or the cluster centroids themselves by adding more information from the data set in their definition besides of using the hard mode. The k-representatives[12] and the k-populations ([9],[1]) are examples of fuzzy k-modes variations. Among the algorithms based on different concepts to cluster data we find the hierarchical method ROCK[17], which uses thenumber of links between objects to identify which are neighbors and belong to the same cluster; the entropy-based algorithms LIMBO[13] and COOLCAT[14]; STIRR[16] based on nonlinear dynamical systems from multiple instances of weighted hypergraphs; GoM a parametric procedure based on the assumption that the data follow a multivariate multinomial distribution ([3],[25])); MADE[3] which uses concepts of the rough set theory to handle uncertainty of the partition; CACTUS[18] based on the idea of co-occurrence between attributes and pairs defining a cluster in terms of a cluster´s 2D projections; the subspace algorithms SUBCAD[11] and CLICK[7] whose main goal is to locate clusters in different subspaces of the data set with the purpose of overcome the difficulties found in clustering high-dimensional data; many other algorithms can be found. Hierarchical agglomerative clustering algorithms such as Single, Complete or Average linkage[15] have also been used to cluster categorical data although non-hierarchical methods are more efficient to handle larger data sets. Many studies are found in the literature comparing the efficiency of clustering algorithms for categorical data. However, most of them uses benchmark data as references to evaluate the performance of the algorithms. The accuracy of the algorithm is then achieved by comparing the reference data with the partition produced by theapplication of the algorithm to the data. By doing so, the performance of the algorithm is dependent upon the relationship between the reference (previous) partition with the categorical variables used to cluster the data. By using this approach, a reasonable clustering algorithm may be considered of poor performance if the previous partition was created by using criteria with no relationship with the observed categorical variables. On the other hand, any algorithm which works well for these particular benchmark data may be considered very accurate. Therefore, simulation studies are also necessary. In Kim et al.[9] the k-populations algorithm was proposed as an extension of fuzzy k-modes. In this method a degree of importance of each category of the variables used to group the data was incorporated in the definition of the clusters centroids. The effectiveness of the algorithm was tested using four benchmark data sets[22] having different composition with respect to the number of clusters (k), number of variables (m) and number of data points (n): the soybean, the zoo database, the credit approval and the hepatitis data. The results showed that k-populations algorithm was more accurated than k-modes, fuzzy k-modes and the hierarchical algorithm using Gower’s similarity coefficient[21]. Although the superiority of k-populations was outstanding, further research is necessary to confirm its accuracy since the algorithm was tested only in four particular data sets. Taking that into consideration, the purpose of this paper is to evaluate the k-populations performance by using Monte Carlo simulation as well as to compare it to four clustering algorithms for categorical data: average linkage, ROCK, k-modes and fuzzy k-modes. The average linkage is a hierarchical procedure available in the majority of the statistical software and it has been proved to be a reasonable method to cluster numerical data (see[8] and[24]). ROCK is very appealing and its good performance has also been demonstrated in studies by using benchmark data sets. However, as far as we know, no paper has been published in the literature comparing these 5 algorithms using reference data sets or Monte Carlo simulation.
2. Clustering Algorithms for Categorical Data
2.1. k-Modes
- The k-modes algorithm proposed by Huang[20] to cluster data on categorical variables is an extension of k-means[23]. It uses a dissimilarity coefficient to measure the proximity of the clusters, modes instead of means, and a frequency-based method to update the modes in each step. Let
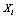 be a sample observation described by
be a sample observation described by 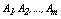 categorical variables being the domain of each
categorical variables being the domain of each 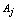 denoted by
denoted by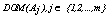 , and let
, and let 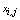 be the observed value of
be the observed value of 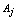 for
for 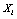 . The objective function of k-modes which has to be minimized, is given by:
. The objective function of k-modes which has to be minimized, is given by: 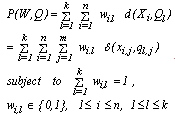 | (1) |
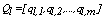 is the vector mode of the cluster
is the vector mode of the cluster  ,
, ,
,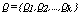 ; m is the number of categorical variables and
; m is the number of categorical variables and 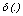 is the dissimilarity measure defined as
is the dissimilarity measure defined as 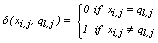 | (2) |
2.2. Fuzzy k-Modes
- The fuzzy k-modes algorithm was proposed by Huang and Ng[19] as an extension of the k-modes and it is based on the fuzzy c-means algorithm used to cluster numerical data[23]. Two new parameters are added in this method: the degree of membership (w) of the observations to each cluster,
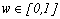 , and the fuzzy parameter denoted by
, and the fuzzy parameter denoted by 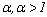 . The membership degrees are estimated in the execution of the algorithm; the fuzzy parameter is fixed in advance and controls the degree of overlapping expected among clusters. In the literature is very common to set
. The membership degrees are estimated in the execution of the algorithm; the fuzzy parameter is fixed in advance and controls the degree of overlapping expected among clusters. In the literature is very common to set 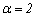 . The degree of chaos in the final partition increases as
. The degree of chaos in the final partition increases as 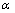 goes to infinity.The objective function of the fuzzy k-modes, which has to be minimized to produce the best partition, is given by
goes to infinity.The objective function of the fuzzy k-modes, which has to be minimized to produce the best partition, is given by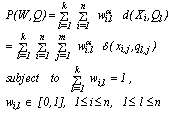 | (3) |
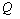 and
and 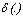 are defined as in section 2.1. According to Huang and Ng[16] the function (3) is minimized if and only if
are defined as in section 2.1. According to Huang and Ng[16] the function (3) is minimized if and only if 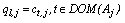 and such that
and such that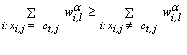 | (4) |
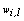 is given as (5). As in k-modes the vector modes may not be unique.
is given as (5). As in k-modes the vector modes may not be unique.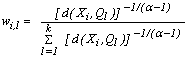 | (5) |
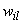 is selected and normalized. It can be randomly chosen from the uniform distribution defined in the[0,1] interval for example; (ii) k initial modes are selected by using equation (4); (iii) all objects are compared to the modes using a dissimilarity measure and allocated to the nearest group; (iv) the
is selected and normalized. It can be randomly chosen from the uniform distribution defined in the[0,1] interval for example; (ii) k initial modes are selected by using equation (4); (iii) all objects are compared to the modes using a dissimilarity measure and allocated to the nearest group; (iv) the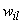 weights are recalculated according to equation (5) and the modes are updated; (v) the steps (iii) and (iv) are repeated till there is no change in the clusters modes.Fuzzy k-modes has been proved to be an efficientclusteralgorithm with the advantage of pointing out the data points which share some similarity with different clusters of the partition and therefore could be misclassified by k-modes-type of algorithms.
weights are recalculated according to equation (5) and the modes are updated; (v) the steps (iii) and (iv) are repeated till there is no change in the clusters modes.Fuzzy k-modes has been proved to be an efficientclusteralgorithm with the advantage of pointing out the data points which share some similarity with different clusters of the partition and therefore could be misclassified by k-modes-type of algorithms. 2.3. k-Populations
- A modification of fuzzy clustering algorithm, called k-populations, was proposed by Kim et. al.[9]. In this new procedure the mode of cluster l, called the population of the lth cluster centroid, is denoted by
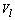 and it is defined as
and it is defined as 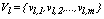 , where
, where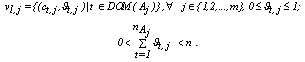 Therefore, the composition of the fuzzy centroids is determined by the categories and by the contribution degree of these categories to the specific cluster,
Therefore, the composition of the fuzzy centroids is determined by the categories and by the contribution degree of these categories to the specific cluster, 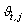 , which is defined as
, which is defined as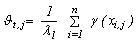 | (6) |
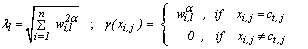 and
and 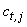 denotes the category t of variable
denotes the category t of variable 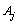 . Briefly speaking, for each category t of the variable
. Briefly speaking, for each category t of the variable 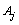 ,
, 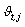 describes the category distribution of the attribute for data belonging to the lth cluster. The normalizing factor
describes the category distribution of the attribute for data belonging to the lth cluster. The normalizing factor 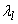 , is the length of the vector
, is the length of the vector 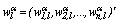 , where
, where 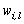 is the degree of membership as defined in section 2.2. According to Kim et. al.[9] the introduction of the
is the degree of membership as defined in section 2.2. According to Kim et. al.[9] the introduction of the 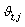 minimizes the imprecision in the representation of cluster centroids and improve the efficiency of the fuzzy clustering algorithm in finding the optimal partition rather than a local optimal. As an illustration suppose there is only one categorical variable with two possible categories
minimizes the imprecision in the representation of cluster centroids and improve the efficiency of the fuzzy clustering algorithm in finding the optimal partition rather than a local optimal. As an illustration suppose there is only one categorical variable with two possible categories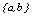 and that for a given cluster l , there are 3 observations
and that for a given cluster l , there are 3 observations 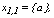
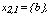 Therefore,
Therefore, 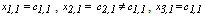 .Let
.Let 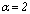 ,
, 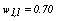 ,
, 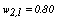 and
and 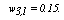 Then,
Then, 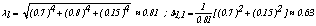 since for the category t=1 of
since for the category t=1 of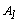 ,
, 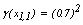 ,
,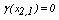 and
and 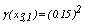 . Similarly, it is found
. Similarly, it is found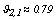 and the fuzzy centroid is given by
and the fuzzy centroid is given by 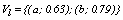 . In k-populations the dissimilarity measure used to compare any observation
. In k-populations the dissimilarity measure used to compare any observation 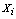 to any fuzzy centroid
to any fuzzy centroid 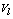 is given by
is given by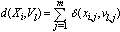 | (7) |
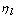 a the normalization factor which corresponds to the length of the vector
a the normalization factor which corresponds to the length of the vector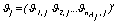 .For k and
.For k and 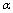 fixed, the basic steps of the k-populations algorithm are given as follows: (i) choose k initial seeds (fuzzy centroids) and the degree of contribution
fixed, the basic steps of the k-populations algorithm are given as follows: (i) choose k initial seeds (fuzzy centroids) and the degree of contribution 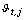 at random; (ii) obtain the proximity matrix between the observations and the fuzzy centroids according to equation (7); (iii) estimate the degree of membership
at random; (ii) obtain the proximity matrix between the observations and the fuzzy centroids according to equation (7); (iii) estimate the degree of membership 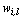 according to the equation (5) and update the fuzzy centroids according to equation (6); (iv) repeat steps (ii)-(iii) until there is no reallocation of objects into clusters.
according to the equation (5) and update the fuzzy centroids according to equation (6); (iv) repeat steps (ii)-(iii) until there is no reallocation of objects into clusters.2.4. The Average Linkage
- The Average linkage is a well-known algorithm used to cluster categorical and numerical data[15]. It starts with each object as its own cluster (step 1); the similarity between clusters are calculated and the two most similar are merged (step 2); this last step is repeated over and over again till the desirable number of clusters k is achieved. Let
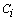 and
and 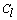 be two clusters with sizes
be two clusters with sizes 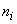 and
and 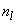 , respectively. In the Average linkage the dissimilarity measure between these two clusters is defined as:
, respectively. In the Average linkage the dissimilarity measure between these two clusters is defined as: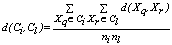 | (8) |
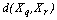 is any dissimilarity measure used to compare the
is any dissimilarity measure used to compare the 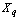 and
and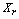 elements. Average linkage does not depend on the notion of initial seeds and therefore, its final partition is not affected by the ordering of the objects in the data set. However, computationally speaking it is less efficient than non-hierarchical algorithms for large data sets.
elements. Average linkage does not depend on the notion of initial seeds and therefore, its final partition is not affected by the ordering of the objects in the data set. However, computationally speaking it is less efficient than non-hierarchical algorithms for large data sets. 2.5. ROCK (RObust Clustering using linKs)
- Different than other cluster algorithms ROCK, proposed by Guha et. al.[17] is based on the notion of links instead of distance or dissimilarity to cluster objects. The number of links between two objects represents the number of neighbors they have in common in the dataset. Let s(.) be a similarity measure. Two observations
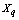 and
and 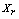 are considered neighbors if
are considered neighbors if 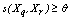 , where
, where 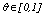 is a pre-specified threshold parameter which controls the amount of similarity required for two observations to be considered neighbors. The
is a pre-specified threshold parameter which controls the amount of similarity required for two observations to be considered neighbors. The 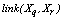 is the number of neighbors the two observations have in common; the higher is its value the more probable is that
is the number of neighbors the two observations have in common; the higher is its value the more probable is that 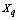 and
and 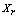 belong to the same group. The main goal is to maximize the sum of links between the observations which belong to the same group and to minimize the sum of links between observations which belong to distinct groups. In practice the implementation of ROCK is as follows: after an initial computation of the number of links between the data objects, the algorithm starts with each cluster being a single object and keeps merging clusters till the specified number of clusters is achieved or no links remain between the clusters. In each step of the algorithm the two clusters which maximizes the goodness measure given in (9) are merged, where
belong to the same group. The main goal is to maximize the sum of links between the observations which belong to the same group and to minimize the sum of links between observations which belong to distinct groups. In practice the implementation of ROCK is as follows: after an initial computation of the number of links between the data objects, the algorithm starts with each cluster being a single object and keeps merging clusters till the specified number of clusters is achieved or no links remain between the clusters. In each step of the algorithm the two clusters which maximizes the goodness measure given in (9) are merged, where 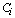 and
and 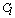 are the clusters being compared and
are the clusters being compared and 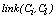 is given by (10). The quantity in the denominator of (9) is approximately the expected number of cross links between the pair of clusters and
is given by (10). The quantity in the denominator of (9) is approximately the expected number of cross links between the pair of clusters and 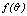 is a pre-specified function. According to Guha et. al.[17] empirical work had been shown that the function
is a pre-specified function. According to Guha et. al.[17] empirical work had been shown that the function 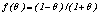 works well in practical situations. Under this function when
works well in practical situations. Under this function when 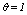 the expected number of links in cluster
the expected number of links in cluster 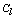 is approximately equal to
is approximately equal to 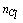 , i.e., each sample point is a neighbor of itself; when
, i.e., each sample point is a neighbor of itself; when 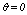 the expected number of links in cluster
the expected number of links in cluster 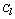 is approximately equal to
is approximately equal to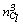 , which corresponds to the situation where all the observations in
, which corresponds to the situation where all the observations in 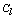 are neighbors of each other.
are neighbors of each other. 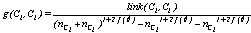 | (9) |
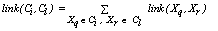 | (10) |
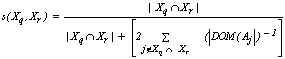 | (11) |
3. Monte Carlo Simulation
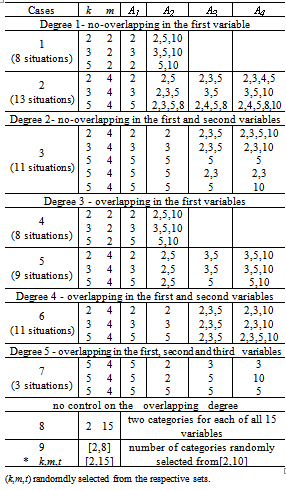
- A total of 64 population structures of clusters were simulated considering different degrees of overlapping among clusters, different number of clusters and categorical variables (k=2,3,5; m=2,4,15) and different number of categories (t=2,3,5,10). Each generated cluster had 50 observations and the population structures of clusters were simulated to possess features of internal cohesion and external isolation. Additionally, one population structure was simulated without pre-setting the values of k,m,t in advance, but by selecting them randomly from the sets: {2,…,8}, {2,…,15} and {2,…,10}, respectively.The main objective of the simulation study was to evaluate the changes in the performance of the clustering algorithms from more stable situations (smaller degree of overlapping, number of clusters, variables and categories), to more complex situations (higher degree of overlapping, number of clusters, variables and categories).
3.1. Data Generation
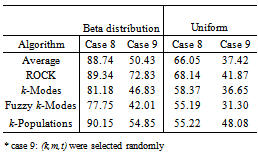
- Table 1 presents the simulated population structures grouped by cases. Each case represents a different situation in terms of overlapping. Clusters without overlapping were generated in cases 1 and 2 (degree 1: non-overlapping in the first variable) and case 3 (degree 2: non-overlapping in the first and second variables). Overlapping clusters were generated in cases 4 and 5 (degree 3: overlapping in the first variable), case 6 (degree 4: overlapping in the first and second variables) and case 7 (degree 5: overlapping in the first three variables). The non-overlapping clusters were built as follows: all observations of the same group had the same category on the first variable (cases 1 and 2) or for the first and the second variables (case 3). The categories of the remaining variables (for m>2) were generated randomly according to the Beta and the Uniform distributions. As an illustration consider case 1, k=2, m=2 and t=2, and suppose that {a,b} are the categories of the first variable. The two clusters were built as follows: for the first variable the category {a} was allocated to all the observations of the first cluster and the category {b} for all observations of the second cluster. For each object the category of the second variable was generated randomly for both clusters. Now consider the case 3, k=5,m=4, the first variable with categories {a,b,c,d,e} and the second variable with categories {f,g,h,i,j}. Then for the first cluster, the categories {a} and {f} were allocated to all objects for the first and second variables, respectively; for the second cluster the categories {b} and {g} were allocated to all objects; and following this procedure for the cluster five the categories {e} and {j}, respectively, were allocated to all objects. For the other two remaining categorical variables the observations were generated randomly for each cluster. The overlapping, (cases 4-7), was performed in such way that all the categories of the variables used to build the overlapping had proportionally the same frequency for each cluster. For example, suppose k=2, m=2, each variable with 2 categories (case 4). Then, the simulation procedure assured that the first category of variable 1 would appear in half of the observations of cluster 1 and the second category in the other half. The observations of the second variable were randomly generated. The same procedure was used for cluster 2. Now suppose k=5, m=4, each variable with 5 categories (case 7). Then for each cluster, for the first, second and third categorical variables, the simulation procedure assured that the frequency of each category would be equal to 20% from all observations from the respective cluster. The observations for the other two remaining categorical variables were generated at random. The proportionality was preserved even in situations where the variables used to build the overlapping had different number of categories. In all situations the generation of the observations for the remaining variables not used in the overlapping procedure, was performed according to the Beta and the Uniform distributions as follows. For each cluster, and each category of the variable
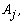 j=1,2,…,m, a random number was selected from the Uniform distribution defined on the[0,1] interval and the Beta distribution with parameters
j=1,2,…,m, a random number was selected from the Uniform distribution defined on the[0,1] interval and the Beta distribution with parameters 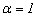 and
and 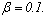 The vector of the generated numbers from each distribution was normalized to describe the probability of observing each category of
The vector of the generated numbers from each distribution was normalized to describe the probability of observing each category of 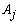 . Data for all categories of
. Data for all categories of 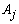 were then generated randomly according to the correspondent normalized probability vector. The Uniform model represents the situation where all categories of
were then generated randomly according to the correspondent normalized probability vector. The Uniform model represents the situation where all categories of 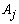 had approximately the same chance of being observed. The Beta distribution was chosen to describe situations where some categories of
had approximately the same chance of being observed. The Beta distribution was chosen to describe situations where some categories of 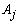 would have higher chance to appear in the sample than others, which is common in practical applications. As an illustration, Figure 1 presents the results of 4 samples of size 50 of a variable
would have higher chance to appear in the sample than others, which is common in practical applications. As an illustration, Figure 1 presents the results of 4 samples of size 50 of a variable 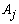 with 3 categories, generated by the described procedure. As it can be seen the Uniform distribution tends to generate classes with similar frequencies different than the Beta distribution which tends to produce classes with larger frequencies than others. Due to the fact that the values for the variables not used to build the overlapping were generated randomly, there is a chance of possible overlapping among the clusters generated in cases 1-3. In the case 8 (k=2,m=2,t=15) there was no control of the overlapping degree among clusters since for each cluster, the observations were randomly selected from the Uniform and Beta distributions. Finally, the case 9 represents the situation where there was no control in the simulation for the number of clusters, variables and categories as well as for the degree of overlapping. For this case, the number of clusters was randomly selected from the set {2,3,…,8}, the number of variables from the set {2,3,…,15} and the number of categories from the set {2,3,…,10}. The observations for each cluster were generated from the Beta and the Uniform distributions, as previously described.From each cluster structure of Table 1 a total of 1000 runs were simulated. The elements of each run were clustered into k groups by using all five clustering algorithms presented in section 2. The resulted partitions were then compared with the true simulated population structure and the performance of the algorithm was evaluated by the average percentage of correct classification taken over 1000 runs (called recovery rate).
with 3 categories, generated by the described procedure. As it can be seen the Uniform distribution tends to generate classes with similar frequencies different than the Beta distribution which tends to produce classes with larger frequencies than others. Due to the fact that the values for the variables not used to build the overlapping were generated randomly, there is a chance of possible overlapping among the clusters generated in cases 1-3. In the case 8 (k=2,m=2,t=15) there was no control of the overlapping degree among clusters since for each cluster, the observations were randomly selected from the Uniform and Beta distributions. Finally, the case 9 represents the situation where there was no control in the simulation for the number of clusters, variables and categories as well as for the degree of overlapping. For this case, the number of clusters was randomly selected from the set {2,3,…,8}, the number of variables from the set {2,3,…,15} and the number of categories from the set {2,3,…,10}. The observations for each cluster were generated from the Beta and the Uniform distributions, as previously described.From each cluster structure of Table 1 a total of 1000 runs were simulated. The elements of each run were clustered into k groups by using all five clustering algorithms presented in section 2. The resulted partitions were then compared with the true simulated population structure and the performance of the algorithm was evaluated by the average percentage of correct classification taken over 1000 runs (called recovery rate).
|
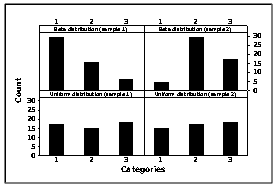 | Figure 1. An illustration of samples from Beta and Uniform distributions. Simulated data – sample size 50 |
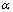 was set as 2 and in the final partition each object was assigned to the cluster whose
was set as 2 and in the final partition each object was assigned to the cluster whose 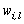 estimate was the largest. The dissimilarity measure given in (11) was used in all algorithms.
estimate was the largest. The dissimilarity measure given in (11) was used in all algorithms.4. Results and Discussion
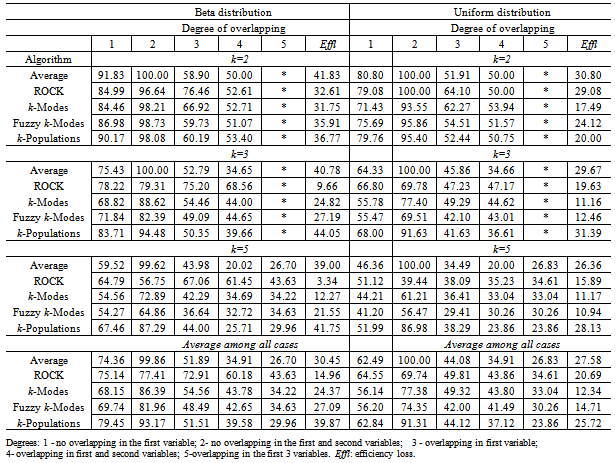
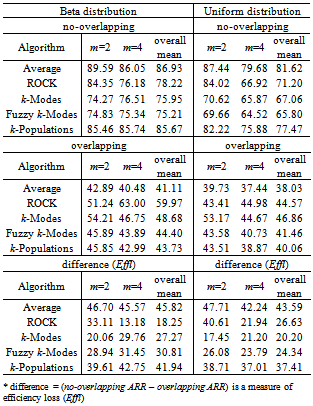
- To evaluate the performance of the algorithms the average of recovery rates (ARR) was calculated considering all factors involved in the simulation procedure: degree of cluster overlapping, number of clusters (k) and variables (m). The results are shown in Table 2 for each algorithm according to the degree of overlapping and the distribution used to generate the data. A weighted overall performance mean is also presented and it was calculated taking into account the fact that the number of simulated models were not the same for each combination of k, m and degree of overlapping. It can be seen that for each clustering algorithm and each k, the larger is the degree of overlapping the smaller is the ARR values, as expected. The same is true when the number of clusters increased. However, the performance loss due to the increase of overlapping degree from 1 to 4 does not necessarily increase with the number of clusters neither is similar for all algorithms. In all situations the average recovery rates were larger for data generated from the Beta distribution. The best results were achieved for k=2 and degrees 1 and 2 of overlapping (for Beta data;
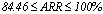 ; for Uniform data
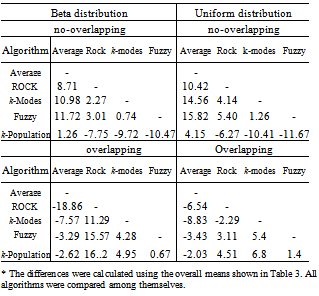
; for Uniform data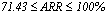 ). When k=2 and the degree of overlapping increased to 3 and 4, the ARR values dropped down ranging from 51.07 to 76.46% (Beta data) and 50 to 64.1% (Uniform data). When k increased to 3 the ARR values decreased ranging from 55.47 to 100% for degrees 1 and 2 of overlapping and from 34.65 to 75.2% for degrees 3 and 4, taking into account data from both distributions. The larger impact took place when k=5 since the majority of the ARR values belongs to theinterval[20,65%] except for average linkage and k-populations which presented ARR values between 70 to 80% for non-overlapping data. Considering all the situations, average linkage and k-populations were the most affected by overlapping as it can be seen by the efficiency loss values (Effl) which is defined as the difference between the ARR values from degrees 1 and 4 of overlapping (see Table 2). On the contrary, ROCK was the less affected and the only method resulting ARR values larger than 50% in all situations for Beta data except for the degree 5 of overlapping, although being also the best in this situation. For Uniform data k-modes was the less affected by overlapping.
). When k=2 and the degree of overlapping increased to 3 and 4, the ARR values dropped down ranging from 51.07 to 76.46% (Beta data) and 50 to 64.1% (Uniform data). When k increased to 3 the ARR values decreased ranging from 55.47 to 100% for degrees 1 and 2 of overlapping and from 34.65 to 75.2% for degrees 3 and 4, taking into account data from both distributions. The larger impact took place when k=5 since the majority of the ARR values belongs to theinterval[20,65%] except for average linkage and k-populations which presented ARR values between 70 to 80% for non-overlapping data. Considering all the situations, average linkage and k-populations were the most affected by overlapping as it can be seen by the efficiency loss values (Effl) which is defined as the difference between the ARR values from degrees 1 and 4 of overlapping (see Table 2). On the contrary, ROCK was the less affected and the only method resulting ARR values larger than 50% in all situations for Beta data except for the degree 5 of overlapping, although being also the best in this situation. For Uniform data k-modes was the less affected by overlapping.
|
5. Final Remarks
|
|
|
|
ACKNOWLEDGEMENTS
- The authors are very thankful to CNPq and CAPESInstitutions.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML