1. Introduction

Increasing muscular strength through resistance training is considered an essential component of physical health and fitness [1]. Greater muscular strength is associated with improved physical ability of daily activities [2,3] and reduced risk of all-cause mortality [4,5]. The one-repetition maximum (1RM) is the most commonly used method to assess dynamic constant external resistance (DCER) muscular strength and is defined as the maximal amount of weight that can be lifted against gravity in a single repetition through a full range of motion [6,7]. In addition, the 1RM assessment can be used to monitor training-induced changes in muscular strength following a DCER training program [8–11]. Having athletes perform frequent 1RM assessments for multiple muscle groups, however, can be impractical for some practitioners. For example, 1RM testing is a trial-and-error method that involves multiple submaximal, maximal, and supramaximal repetitions which can consume a large amount of time [6,12–14], accumulate unwanted fatigue that can lead to a potential injury [15–17], and undermine the amount of time and effort devoted to training [7,11]. Therefore, an alternative to 1RM testing is to use equations (EQs) that estimate 1RM from repetitions to failure (RTF) performed at a submaximal weight [7,11,12,18–21].

A number of regression EQs have been developed [13,21–32] to estimate 1RM values from RTF with submaximal weights ranging from 20-95% of 1RM for a variety of specific movements [21,23,25,26,29,31,33–35]. In addition, generic EQs have been developed that are not limited to a specific movement and can be utilized for a variety of different movements [22,24,27,28,30,32]. In some cases, however, the derivation studies of these generic EQs provided limited information regarding the sample characteristics (i.e. years of resistance training experience) and/or the derivation methodology (i.e. equipment, number of RTF, and weight used), making it difficult to determine their external validity.

Previous studies have used cross-validation procedures to quantify the accuracy of EQs to estimate 1RM values on independent samples of subjects [9,12,14,17,19,29,36]. These studies examined the validity of the EQs using correlation coefficients and constant error values (CE = mean difference between estimated and measured 1RM values). In general, the EQs that most accurately estimated a single assessment of 1RM exhibited correlation coefficients and CE values of approximately 0.85 to 0.99 and -0.9 kg to 2.1 kg, respectively. Few studies, however, have included total error (TE) values to determine the validity of these EQs [17,18,21,37]. The TE represents the true difference between estimated and measured 1RM and is the single best criterion for quantifying the prediction error [21,38–41]. Cross-validation studies, therefore, should also include the TE when determining the validity of EQs in estimating 1RM values from a single assessment.

If EQs are to be used as an alternative to the direct assessment of 1RM [11], their external validity would be increased if they demonstrated a high degree of validity for estimating 1RM values before and after training. Braith et al. [23] reported, however, that separate linear EQs were required to accurately estimate pre- and post-training leg extension (Leg Ex) 1RM with 7-10 RTF. Previous studies that have examined the predictive ability of these EQs across a resistance training intervention [8–10,16,23,42] have reported inconsistent findings due to factors such as the movement performed (i.e. upper versus lower body, the number of muscle groups involved), the sample characteristics (i.e. gender, years of resistance training experience, etc.), the methodology used (i.e. number of RTF and weight used), and the type of EQ (i.e. exponential versus linear). Brechue and Mayhew [8,9] and Mayhew et al. [16] reported estimations within ± 5% of measured post-training bench press and squat 1RM values with submaximal weights between 80% and 90% compared to approximately ± 12% for weights between 60% and 80% of 1RM using exponential EQs. Thus, previous reports [8–10,16,42] have recommended the use of submaximal weights that are greater than 80% of 1RM for accurately estimating post-training 1RM values regardless of the type of EQ used.

It is possible that a change in relationship between the RTF and training weight during a resistance training program influences the accuracy of the EQs for estimating training-induced changes in 1RM [23,43]. Few studies [8,16,42] have investigated if EQs can accurately track the training-induced changes in bench press 1RM values, and only Roberts et al. [10] investigated their predictive ability for estimating training-induced changes in 1RM for the lower body (i.e. Leg Ext). Roberts et al. [10], however, used submaximal weights between 33.9 and 75.8% of post-training 1RM to estimate post-training and training-induced changes in 1RM, resulting in large TE values (21.9 kg to 39.1 kg and 21.0 kg to 31.9 kg, respectively). Therefore, the purpose of this study was to cross-validate 5 EQs for estimating pre-training, post-training, and absolute training-induced changes in Leg Ext 1RM with RTF weights that are ≥ 80% of 1RM. Based on previous studies [8,9,16,42], it was hypothesized that the EQs would accurately track training-induced changes in Leg Ext 1RM.

2. Methods

2.1. Subjects

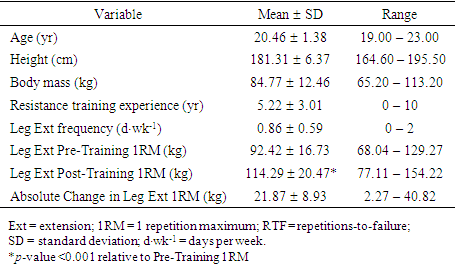
Thirty-five men volunteered to participate in the present study. Seven of the volunteers, however, voluntarily withdrew due to reasons unrelated to the study. Therefore, twenty-eight men (mean ± SD: age = 20.46 ± 1.38 yrs; height = 181.31 ± 6.37 cm; body mass = 84.77 ± 12.46 kg) completed this study (Table 1). Prior to participating the study, all subjects reported no lower body pathologies that would affect their Leg Ext performance. The subjects were recreationally active [44] and reported participating in the following activities for a minimum of 1 day per week prior to the start of the study: Resistance training (n = 23), aerobic training (n = 23), running (n = 2), swimming (n = 1), biking (n = 2), flag football (n = 2), basketball (n = 6), volleyball (n = 3), softball (n = 1), broomball (n = 1), and yard work (n = 1). Most subjects had previous resistance training experience (experience = 5.22 ± 3.01 yrs) and included the Leg Ext movement in their exercise rotation (0.86 ± 0.59 days per week; Table 1). The subjects were informed of the benefits and risks of participation in the study, signed a written Informed Consent form, and completed a Health History Questionnaire. The ethical principles in the present study were approved by an institution affiliated with one of the authors.

Table 1. Subject Characteristics and Leg Extension Performance (n = 28)

2.2. Study Design

The subjects visited the laboratory on 26 occasions over a 10-week period. During the first visit, demographic information was collected, the subjects were familiarized with the resistance training procedures, and their pre-training bilateral Leg Ext 1RM was assessed. The subjects then began the 8-week bilateral Leg Ext DCER training program which included 24 training sessions each separated by a minimum of 24 hours. The resistance training sessions consisted of 2 warm-up sets of 8 repetitions and 1 working set of RTF at approximately 80% of 1RM. At least 48 hours after the last training session, the subject’s post-training bilateral Leg Ext 1RM was assessed. The present study cross-validated five EQs to estimate pre-training, post-training, and absolute training-induced changes in bilateral Leg Ext 1RM using the weight and RTF values from the first and last training sessions.

2.3. One-Repetition Maximum

The bilateral Leg Ext 1RM test was performed on a plate-loaded Hammer Strength Iso-Lateral resistance machine (Hammer Strength, Cincinnati, OH). Before testing, the subject’s maximal Leg Ext range of motion was determined using a ruler fastened to an adjustable tripod (Figure 1). While the subject’s legs were fully extended, an investigator adjusted the height of the tripod to contact the shin pad bar of the Leg Ext machine. The height of the ruler was recorded and used to standardize the subject’s range of motion for all testing and training visits. The 1RM testing protocol followed the guidelines established by the National Strength and Conditioning Association for lower body movements [45]. The warm-up included one set of 5-10 repetitions with a light weight, a second set with a heavier weight that would result in 3-5 repetitions, and a third set with a near maximal weight that could be completed in 2-3 repetitions. The subjects were given 1-2 minutes of rest between each warm-up set and 2-4 minutes of rest between the last warm-up set and the first 1RM attempt. The first 1RM attempt was performed with a 13.6-18.1 kg increase in weight from the final warm-up set. If the subsequent 1RM attempt were successful, the weight was increased by 13.6-18.1 kg. If an attempt was unsuccessful, the weight was decreased by 4.5-6.8 kg. The weight was increased or decreased by an investigator until the subjects successfully completed a 1RM, and the smallest change in weight possible between attempts was 2.3 kg. The determination of 1RM typically required 3-5 attempts each separated by 2-4 minutes of rest. The subjects were given strong verbal encouragement by the investigators during all 1RM attempts. The 1RM attempts were considered successful if the subject reached full extension as determined by the ruler fastened to the tripod.

Figure 1. The leg extension set up for testing and training

2.4. Resistance Training

The Leg Ext DCER training visits were performed 3 days per week for 8 weeks. The training visits consisted of 2 warm-up sets and 1 working set to failure. The two warm-up sets consisted of 8 repetitions at approximately 50% and 70% of the pre-training 1RM and the single working set consisted of RTF at approximately 80% of the subject’s pre-training 1RM. To ensure the subjects reached their maximum number of repetitions, strong verbal encouragement was given by an investigator and 2-5 minutes of rest was allowed between sets. A repetition was considered successful if that the shin pad bar contacted the ruler. The task was terminated when the subjects could no longer contact the ruler with the shin pad bar for 2 consecutive repetitions or when the subjects voluntarily decided to end the task. The weight adjustment for subsequent training sessions depended on the number of repetitions completed during the working set. If the subject completed 8-9 or ≥ 10 RTF, the weight for the warm-up and working sets was increased by 2.3 or 4.5 kg, respectively. If the subjects completed ≤ 7 RTF, however, the weight for the subsequent training session remained unchanged for the warm-up and working sets.

2.5. Equations for Estimating One Repetition Maximum

The EQs in the present study were selected based on the findings from two recent cross-validation studies [10,21] specific to the Leg Ext movement. Of the 8 EQs cross-validated by these studies [10,21], 5 EQs [21,26,28,30,32] met the inclusion criteria of a TE value less than 15 kg. The EQs in the present study (Table 2) used either a linear model (EQs 2 and 3) or an exponential model (EQs 1, 4, and 5) to estimate 1RM values from RTF. Of the 5 EQs, only EQ 2 [26] was derived specifically from the Leg Ext movement, while EQs 1, 3, and 5 are generic EQs and not limited to a specific movement (Table 2). Equation 4 was derived by adding the cross-validation constant error (CE = mean difference between estimated and measured 1RM values) from Roberts et al. [21] to the y-intercept of the original EQ of Lombardi [28] (EQ 1) based on the recommendation of Lohman [46].

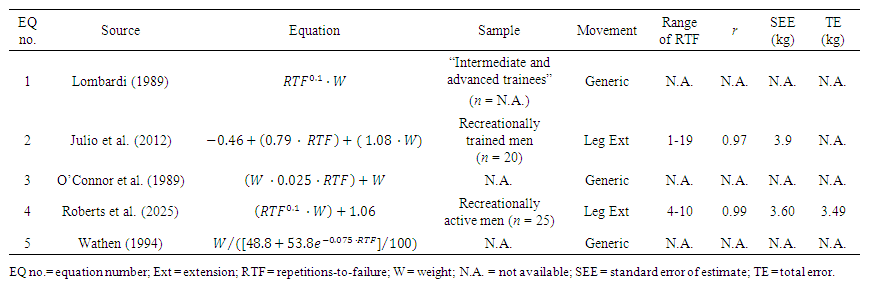Table 2. The equations used in the cross-validation analyses and derivation methodologies

2.6. Statistical Analysis

The pre-training to post-training absolute changes in the measured Leg Ext 1RM as well as the RTF weight, the RTF weight as a % of pre-training 1RM, and number of RTF values from the first and last training session were analyzed with paired t-tests. Estimated pre-training 1RM, estimated post-training 1RM, and estimated absolute training-induced changes in 1RM values were statistically cross-validated by examining the CE values using paired t-tests, Pearson Correlation Coefficients (r), standard error of estimates (SEE), and TE values using the following equation:

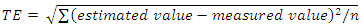(1)

The CE reflects the systematic bias between the estimated and measured 1RM and absolute change values. Pearson Correlation Coefficients describe the magnitude of the relationship between the estimated and measured 1RM and absolute change values. The following r values were used to classify the magnitude of the relationship [47]: very weak (r < 0.20); weak (r = 0.20 to 0.39); moderate (r = 0.40 to 0.59); strong (r = 0.60 to 0.79); and very strong (r = 0.80 to 1.00). The SEE quantifies the error associated with the regression line for the relationship between estimated and measured 1RM and absolute change values. The TE includes the combined errors associated with the CE and SEE and reflects the error around the line of identity for the estimated versus measured 1RM and absolute change values.

The accuracy of the estimated 1RM and absolute change values were determined with the following cross-validation criteria [38,40,41,48]: (a) The estimated and measured mean values should be comparable; (b) there should be close agreement between the estimated and measured SD values; (c) a low SEE value is desirable and is preferred over the Pearson Correlation Coefficient because correlations are affected by differences between samples in the variability of 1RM values; (d) the TE should be calculated because it reflects the true difference between the estimated and measured values, while the SEE reflects only the error associated with the regression between the variables; and (e) a close similarity between the SEE and TE indicates a CE value near zero and little difference between the regression lines for the measured and estimated 1RM values and the line of identity. Although all criteria were considered, primary attention was given to the TE values because the TE is the best single criterion for quantifying the error between estimated and measured values [41]. An alpha level of p ≤ 0.05 was used to determine statistical significance. All statistical analyses were performed using IBM SPSS version 29 (SPSS Inc, Armonk, NY).

3. Results

The subjects completed an average of 22 (91.20 ± 6.36%) of the 24 training visits, with a range of 20-24 (83.33 to 100%) visits completed. The subjects’ pre-training, post-training, and absolute training-induced changes in Leg Ext 1RM are presented in Table 1. The absolute changes in the RTF weight (23.08 ± 7.61 kg), RTF weight as a % of pre-training 1RM (25.12 ± 7.34%), and number of RTF (0.64 ± 3.09 repetitions) are presented in Table 3. There was a significant increase (p < 0.001) in absolute Leg Ext 1RM from pre-training (92.42 ± 16.73 kg) to post-training (114.29 ± 20.47 kg). The RTF weight and the RTF weight as a % of pre-training 1RM increased significantly (p < 0.001) from the first-training session (76.57 ± 13.36 kg and 82.97 ± 2.94%, respectively) to the last-training session (99.69 ± 17.83 kg and 108.10 ± 7.26%, respectively), while the number of RTF were not different (p = 0.281) between the first and last training sessions (6.46 ± 2.17 repetitions and 7.12 ± 2.15 repetitions, respectively).

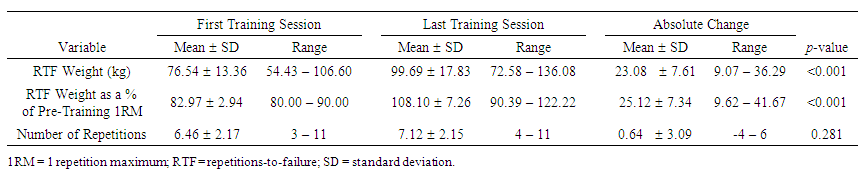Table 3. Leg Extension Performance Characteristics of the Subjects (n = 28)

The cross-validation results for the estimated pre-training Leg Ext 1RM are presented in Table 4. Equations 2 and 3 underestimated the mean measured pre-training 1RM value, with CE values of -5.10 kg (EQ 2) and -3.45 kg (EQ 3). There were no significant (p = 0.505 to 0.655) CE values for EQ 1 (-0.62 kg), EQ 4 (0.44 kg), and EQ 5 (1.00 kg). All EQs exhibited very strong (r = 0.91 to 0.97) correlations [47] between estimated and measured pre-training Leg Ext 1RM values. The SEE and TE values for the EQs ranged from 4.05 kg (EQ 2) to 7.25 (EQ 5) and 5.09 kg (EQ 4) to 7.73 (EQ 5), respectively. The difference between the estimated and measured SD values for pre-training 1RM ranged from 0.00 kg (EQ 3) to 1.67 kg (EQ 5). The similarities between the measured and estimated SEE and TE values for 1RM values ranged from 0.08 kg (EQ 1) to 2.56 kg (EQ 2).

Table 4. Results of the Cross-Validation Analyses for Estimating Pre-Training Leg Extension One-Repetition Maximum (kg) from the Repetitions-to-Failure During the First-Training Session

The cross-validation results for the estimated post-training Leg Ext 1RM values (Table 5) demonstrated that EQs 1, 3, 4, and 5 overestimated (p ≤ 0.016) the mean measured post-training 1RM value, with CE values ranging from 3.30 kg (EQ 3) to 9.92 kg (EQ 5). The mean for EQ 2, however, was not significantly different (p = 0.167) from the measured post-training 1RM value (CE of -1.53 kg). All EQs exhibited very strong (r = 0.95 to 0.96) correlations [47] between estimated and measured post-training Leg Ext 1RM values. The SEE and TE values for the EQs ranged from 5.82 kg (EQ 2) to 6.71 kg (EQ 5) and 5.82 kg (EQ 2) to 13.19 kg (EQ 5), respectively. The difference between the estimated and measured SD values for the post-training 1RM ranged from -0.67 kg (EQ 2) to 4.38 kg (EQ 5). The similarities between the measured and estimated SEE and TE values for the 1RM values ranged from 0.00 kg (EQ 2) to 6.48 kg (EQ 5).

Table 5. Results of the Cross-Validation Analyses for Estimating Post-Training Leg Extension One-Repetition Maximum (kg) from the Repetitions-to-Failure During the Last-Training Session

For the absolute training-induced changes in Leg Ext 1RM (Table 6), all the EQs significantly (p ≤ 0.006) overestimated the mean measured absolute change in Leg Ext 1RM value, with CE values ranging from 3.57 kg (EQ 2) to 8.93 kg (EQ 5). All the EQs demonstrated strong (r = 0.67 to 0.75) correlations [47] between the estimated and measured absolute change 1RM values. The SEE and TE values ranged from 6.04 kg (EQ 2) to 6.87 kg (EQ 5) and 7.16 kg (EQ 2) to 14.29 kg (EQ 5). The difference between the estimated and measured absolute change in SD values ranged from 10.87 kg (EQ 2) to 16.36 kg (EQ 5). The similarities between the measured and estimated SEE and TE values for the absolute change in 1RM ranged from 1.12 kg (EQ 2) to 7.42 kg (EQ 5).

Table 6. Results of the Cross-Validation Analyses for Estimating Absolute Training-Induced Changes in Leg Extension One-Repetition Maximum (kg) from The Repetitions-to-Failure During the First- and Last-Training Sessions

4. Discussion

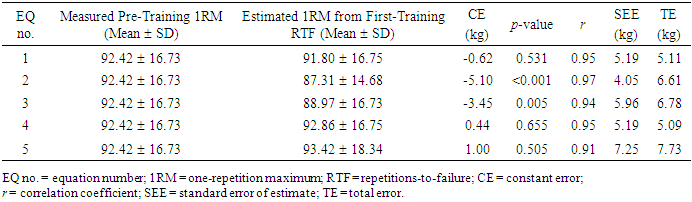
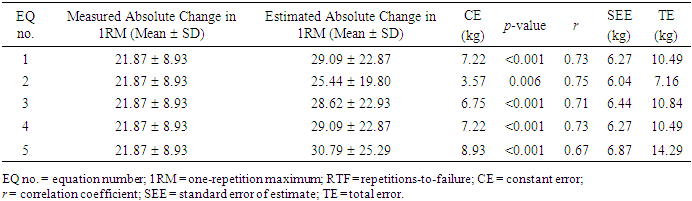
The purpose of this study was to use cross-validation procedures to determine the accuracy of 5 EQs for estimating pre- and post-training Leg Ext 1RM values from the weights performed and RTF during the first- and last-training sessions and quantify the error for estimating training-induced changes in 1RM from the EQs in recreationally active men. In the present study, the mean pre-training Leg Ext 1RM normalized to body mass ([92.42 kg / 84.77 kg] x 100 = 109%) was less than that reported by Roberts et al., [10] for an independent sample of recreationally active men (155%). In addition, the 8 weeks of Leg Ext DCER training in the present study resulted in a 23.66% mean increase in Leg Ext 1RM which was comparable to the study of Roberts et al. [10] that reported an increase of 27.27% following an 8-week Leg Ext DCER training protocol.

In the present study, the mean values for the estimated pre-training 1RM from EQs 2 and 3 differed significantly from the mean measured pre-training 1RM, while EQs 1, 4, and 5 exhibited no mean differences between the estimated and measured pre-training 1RM (Table 4). These findings were not consistent with those of previous cross-validation studies for the Leg Ext movement [10,21,37]. For example, previous studies [10,21,37] have reported that EQ 5 overestimated the mean measured pre-training 1RM (CE = 3.61 to 10.2 kg). The differences between the results of the present study and those of Wood et al. [37] may be attributable to age (54.22 ± 3.12 yrs) related differences in muscular strength and endurance [49,50] compared to the sample in the present study (20.46 ± 1.38 yrs). The findings of Roberts et al. [10,21], however, may be attributable to the greater number of RTF performed (4-17 repetitions and 4-21 repetitions, respectively) compared to the present study (3-11 repetitions). The improved accuracy from the range of RTF performed in the present study, compared to that of Roberts et al. [10], was consistent with previous studies [8,9,16,17,43,51] that have reported more accurate estimations of 1RM with lower (≤ 10) rather than higher RTF ranges for lower and upper body movements. In addition, all EQs in the present study exhibited very strong correlations (r = 0.91 to 0.97) between the estimated and measured pre-training Leg Ext 1RM values, which were consistent with previous cross-validation studies for lower body strength exercises including the squat, deadlift, and Leg Ext [10,12,21,37]. Furthermore, in the present study, EQs 1 and 4, demonstrated small differences between the SEE and TE values (0.08 kg and 0.10 kg, respectively), with EQ 4 exhibiting the lowest TE value of 5.09 kg (Table 4). This TE accounted for 5.50% of the mean pre-training 1RM (92.42 kg) and, therefore, EQ 4 provided the most accurate estimates of pre-training Leg Ext 1RM.

For the post-training estimates (Table 5), four of the five EQs (EQs 1, and 3-5) overestimated the mean measured post-training Leg Ext 1RM with CE values that ranged from 3.30 kg (EQ 3) to 9.92 kg (EQ 5). There was no mean difference, however, for EQ 2 for the post-training Leg Ext 1RM estimations with a CE value of -1.53 kg. All the EQs exhibited very strong correlations (r = 0.95 to 0.96) between the estimated and measured 1RM values (Table 5). In addition, the SEE and TE values ranged from 5.82 kg (EQ 2) to 6.71 kg (EQ 5) and 5.82 kg (EQ 2) to 13.19 kg (EQ 5), respectively. These findings were not consistent with those of Roberts et al. [10] who reported that EQs 1-3 underestimated the post-training Leg Ext 1RM values (CE = -35.6 kg to -9.4 kg and TE = 21.9 kg to 39.1 kg) following 8 weeks of resistance training. It is likely that the lower TE values in the present study, compared to those of Roberts et al., [10], can be explained by the weights and number of RTF used to estimate the post-training 1RM values. The weights used to estimate post-training Leg Ext 1RM values in the present study ranged from 90.39% to 122.22% of pre-training 1RM and resulted in 4-11 RTF, while Roberts et al. [10] reported using 80.0-83.3% of pre-training 1RM (equivalent to 33.9% to 73.8% of post-training 1RM) and resulted in 11-37 RTF. The improved accuracy in the present study, compared to that of Roberts et al. [10], supported previous reports [8,9,17,18,43,51] of greater accuracy in estimating 1RM values when using heavier weights (≥ 80% of 1RM) that result in fewer RTF (≤ 10) than those that used lighter weights and greater RTF. Furthermore, in the present study, the TE values expressed as a percentage of the mean measured post-training 1RM (114.29 kg) were greater for all the EQs, except for EQ 2, when compared to their respective pre-training estimates of 1RM (Table 4). Specifically, EQ 2 demonstrated a lower TE value equivalent to 5.09% of the mean measured post-training 1RM (114.29 kg) versus 7.15% of the mean measured pre-training 1RM (92.42 kg). Thus, 4 of the 5 EQs in the present study, demonstrated greater error for estimating the post-training 1RM than the pre-training 1RM.

Eight weeks of Leg Ext DCER training in the present study resulted in a mean increase of 21.87 kg (23.66%) in Leg Ext 1RM and the subjects were able to complete a greater percentage of 1RM from the first training session (82.97 ± 2.94%) to the last training session (87.41 ± 5.28%), with no difference in RTF (3-11 and 4-11 repetitions, respectively). For estimating the absolute training-induced increases in Leg Ext 1RM, all the EQs overestimated (CE = 3.57 kg to 8.93 kg) the mean measured training-induced increases. Furthermore, the SEE values ranged from 6.04 kg (EQ 2) to 6.87 kg (EQ 5) and TE values ranged from 7.16 kg (EQ 2) to 14.29 kg (EQ 5). All of the EQs demonstrated strong relationships (r = 0.67 to 0.75) between the mean estimated and measured absolute training-induced increases in Leg Ext 1RM values, and the TE values relative to the mean measured absolute increase in 1RM value (21.87 kg) ranged from 32.74% to 65.36%. The results of the present study were not consistent with those of Roberts et al. [10], who reported TE values of 69.36% to 94.23% (relative to the measured absolute change in 1RM of 34.6 kg), likely due to the lighter post-training RTF weights (33.9% to 73.8% of 1RM) used in the EQs. Therefore, the present findings suggested that performing RTF with weights that are greater than 80% of 1RM can reduce the error associated with estimating the training-induced increases in Leg Ext 1RM. Despite the reduced error observed with weights greater than 80% of 1RM, none of the EQs in the present study accurately estimated the training-induced increases in Leg Ext 1RM following 8 weeks of resistance training.

The inability of the EQs to accurately estimate the training-induced increases in 1RM can be explained by comparing each EQ’s post-training estimated values to their respective pre-training estimated values. The EQs in the present study that did not demonstrate similar accuracy for estimating pre- and post-training 1RM resulted in large errors for estimating the training-induced increases in 1RM (Table 6). In the present study, a greater proportion of subjects achieved or surpassed the target of 8 repetitions during the last training session (53.57%) at ~90% of 1RM compared to the first training session (39.29%) at ~80% of 1RM. It is likely that a change in the relationship between RTF and training weight from the first to last training session may have affected the accuracy of the EQs for estimating post-training Leg Ext 1RM and, therefore, the training-induced increases in Leg Ext 1RM. Future studies are needed to examine the effect of resistance training interventions with a lower repetition target (e.g., 3-5 repetitions) on the relationship between RFT and training weight as well as the predictive ability for linear and exponential EQs to estimate post-training and training-induced increases in 1RM.

The results of this study were limited to young, recreationally active men and the bilateral Leg Ext movement. Thus, the current findings cannot be extrapolated to men in different age groups, women, or other movements. Future studies are needed to examine the validity of previously published EQs for estimating upper and lower body 1RM in these populations and for various movements. Furthermore, the current study utilized the Hammer Strength (Hammer Strength, Cincinnati, OH) Leg Ext machine and it is unknown if the current findings would be replicated using other equipment.

5. Conclusions

The findings of the present study indicated that EQ 4 most accurately estimated pre-training Leg Ext 1RM, while EQ 2 provided the most accurate estimate of post-training 1RM. None of the EQs, however, accurately quantified the absolute training-induced increase in Leg Ext 1RM. Therefore, it is recommended that EQ 4 be used to estimate pre-training 1RM and EQ 2 for post-training 1RM in young, recreationally active men for the bilateral Leg Ext movement. None of the EQs, however, were suitable for assessing training-induced increases in Leg Ext 1RM.

ACKNOWLEDGEMENTS

The authors would like to thank the subjects for their participation in this study.