Joe Roith, Rhonda Magel
Department of Statistics, North Dakota State University, Fargo, ND, USA
Correspondence to: Rhonda Magel, Department of Statistics, North Dakota State University, Fargo, ND, USA.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This research examines two aspects of hockey teams in the National Hockey League (NHL). The first aspect of the research was to determine significant seasonal factors and corresponding weights using discriminant analysis in predicting which teams would make the playoffs. Data was collected over seven seasons initially considering 60 variables. Total goals against, total goals scored, and takeaway totals for a season, were enough to correctly predict whether a team made the playoffs 87% of the time. The second aspect of this research uses regression analysis to create models estimating the probability of a hockey team winning the game, and also estimating the difference in goals scored between the two teams playing in the game. In developing these models, a random sample of games was taken from the 2009-10 and 2010-11 season and the in-game values on 60 variables were recorded. A logistic model was then developed estimating the probability that a team would win the game if the values of the following in-game variables found to be significant were known: save percentage margin, shot margin, block margin, short-handed faceoff percentage, short-handed shot margin, and even-handed faceoff percentage. A second model was formed for estimating the goal difference of a game that was also based on the random sample of 52 games taken from the 2009-10 and 2010-11 seasons. In the goal difference model, save percentage margin and shot margin were significant and accounted for over 93% of the variation in score difference. The probability model and the goal difference model were validated using the actual in-game values from a different data set that was not used in the development of the models. The probability model and the goal difference model were correct 98% and 100% of the time for these 52 games when the actual in-game values of the variables were used. The probability model and the goal difference model were then used in predicting the results of another random sample of 60 hockey games from the 2011-12 season when the actual in-game values of the variables were not used, but instead averages of the values of these variables were used based on the previous three hockey games both teams had played. In this case, the models correctly predicted the results of the hockey games 65% and 66.7% of the time. These percentages were found to be significantly larger than the percentages of the time one correctly predicted the winner of a game by always selecting the home team, or always selecting the team with the better record, or always selecting best team as determined by a handicapping website. It was found also both over the entire season and over the short term that defense has a stronger impact on winning the game than offense. Perhaps teams may want to rethink their most important players.
Keywords:
Stanley cup playoffs, Defensive statistics, Offensive statistics, Least squares regression, Logistic regression, Discriminant analysis
Cite this paper: Joe Roith, Rhonda Magel, An Analysis of Factors Contributing to Wins in the National Hockey League, International Journal of Sports Science, Vol. 4 No. 3, 2014, pp. 84-90. doi: 10.5923/j.sports.20140403.02.
1. Introduction
The National Hockey League (NHL) is a $3 billion a year industry with thirty franchises throughout the United States and Canada. Because of this, teams put millions of dollars into their coaching staffs, player development, and scouting for players. Teams want to be successful and will often try to copy what other successful teams have done. Is one aspect of what they are doing emphasized too much or too little? In this research, we will develop models to help determine which factors are significant in predicting, or have influence, in which team will win a game. We will also use discriminant analysis to determining which factors are significant in whether a team is successful at making the playoffs.In the NHL, teams are split into two conferences, East and West. The East conference is divided into two divisions of seven teams each. The West conference is divided into two divisions of eight teams each. All teams play eighty-two games in a typical regular season. Every time a team wins, they receive two points with the points accumulating over the year. If a team loses in regulation play, they receive zero points. If a team loses during overtime play, or during the round of shootouts, they will claim one point towards their total number of points. At the end of the season, the teams are ranked by the total number of points they are able to collect and from these rankings are determined eligible for playoffs or not. The top three teams from each division make the playoffs with the remaining spots going to the two teams in each conference with the highest number of points, regardless of the division. This will constitute the 16 team playoff for the Stanley Cup.Research in this paper will be divided into two separate areas; the examination of the outcome for a team over the entire season, and then the examination of the outcome of a team for a single game. We will determine which factors are significant in the seasonal success of a team where a team is considered to be successful for the season if they make the playoffs. We will also determine which factors are significant for a team in winning a single game.Data in this research was collected on NHL games and seasons from 2005-06 to 2011-12 to examine the seasonal success of teams and from seasons 2009-10 to 2011-12 to examine the outcomes from single games. Seasons previous to these years were played under slightly different rules. After the labor strike in 2004, rules were changed with the specific intention to increase scoring in the game. Therefore, any assumptions of identical distribution of outcomes from game to game are violated when using those pre-strike observations. Another labor strike that was resolved in early 2013 was primarily based in the economic foundations of the game and focused on financial agreements between players and owners. The settlement of that dispute did not result in the change of any rules regarding game play, and thus, the findings of this research should still be applicable.
2. Past Research
There has been extensive research into the game of hockey. However, the majority of the research has been focused on goal scoring and the distribution of goal scoring. Ryder [1] suggests that goal scoring in the NHL follows a Poisson distribution. This results in looking at competing Poisson processes when trying to predict the outcome of the games. Ryder shows that by breaking down the scoring in hockey into short time intervals, one can accurately predict goals, except in the last two minutes when scoring is greatly increased due to the occasional strategy of pulling the goalie for an extra attacker when a team is down by one or two goals.Ryder [1] takes a similar approach to the research in this paper by focusing on the outcomes of individual games and also by examining the bigger picture of what is happening in terms of the whole season. If the average goals scored per game for both teams, say “team of interest” and “opposing team”, playing in a contest is known, Ryder’s method, gives the probabilities of the “team of interest” winning by z amount of goals. These probabilities, for each value z, can be added together to obtain the estimated probability of the “team of interest” winning the game. Ryder also derives a table estimating the “team of interest’s” winning percentage for the season based on the average goals per game and the average opponents’ goals per game. For instance if the “team of interest” averages 2.5 goals per game throughout the season, and gives up an average of 2.5 goals per game, we can expect their winning percentage to be 0.500 for the season. However, if the “team of interest” averages 4.0 goals per game and gives up an average of 3.5 goals per game, their winning percentage is expected to be about 0.566.In another paper, Ryder [2] considers more empirical methods towards predicting the outcome of games. The only two variables Ryder considers are goals scored and goals against. He begins with a linear regression approach and then moves to some non-linear approaches. Equation (1) shows the general form of his results using Goals For (GF), Goals Against (GA), Goals For per Game (GFg), and Goals Against per Game (GAg).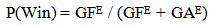 | (1) |
Where E = (GFg + GAg)0.458With this formula, Ryder was able to model games in post WWII NHL with an R-square of 0.941[2]. Ryder [2] does give us a much better understanding of the extent to which more scoring will increase the likelihood of winning, but it does nothing to give a team ideas as to what could lead to their success.Thomas [3] also assumed the distribution of goals scored in a hockey game follows a Poisson distribution and simulated probabilities of a team winning the game under various circumstances. For example, Thomas estimated the probability of a team winning when leading by two goals with forty minutes remaining to be 0.808. He estimated the probability of a team winning with one minute remaining to be 0.946. Thomas provided teams with some useful information. When a team is down by two goals with twenty minutes of the game left, Thomas calculated a team increases their chance of winning by 10% if they score the next goal, but if the opposing team scores the next goal, the team’s percentage of winning is about 0%.In other research conducted by Thomas [4], he considered the Harvard ice hockey team and made the argument that hockey can be described as a continuous time semi-Markov process. Thomas separated the game of ice hockey into 19 distinct states including; offensive team with the puck in defensive zone, defensive team with the puck in the offensive zone, faceoff at center ice, defensive takeaway, among others. From there, Thomas calculated the expected number of goals scored in each state as time increases. The expected value of goals is much higher for each state as the time in that state increases. When the situation shifts to a different state, the time is reset. It is noted that not all states are equal. At 40 seconds, the expected number of goals while in the offensive giveaway state is higher than the expected number of goals 40 seconds into a defensive possession state for the “team of interest”, or in this case, the Harvard ice hockey team. The implications here are more strategy based. How do different aspects of the game differ considering goals? Thomas does compare common defensive plays to see which ones result in more frequent scoring. Work here was done on one team, but similar work could be done with other teams, including teams in the NFL.One topic often discussed in sports is the magnitude of the offense compared to the defense. It has long been the consensus from analysts and coaches that defense wins championships. Moskowitz and Wertheim [5] disagree with that statement. They considered multiple sports, including hockey, and tried to determine if teams who were ranked as a top defensive team won championships more often than those who were ranked as a top offensive team. In every sport they looked at, there were just as many offensive teams winning as there were defensive teams winning. Teams however, were categorized based only on rankings from the seasonal performances, and only playoffs and championships are considered. We still believe that in a game by game setting, defense has a more important role and if a team would like to make the playoffs, having a defensive mindset during the season will be a better way to achieve that.This research will look at more subtle aspects of the game of ice hockey that may be indicators of a style of play that leads to more success. We will consider various variables that are kept in the game of ice hockey and determine which of these variables are significant, and how the game variables are weighted in relation to one another in determining whether a team will have a successful season, and then in determining the winner of a single ice hockey game.
3. Design of Study
The purpose of this research is to analyse what variables may influence winning in the NHL. In particular, what factors of the game should be emphasized to be successful over the course of a season and what factors should be emphasized to win an individual match. For example, is it more important for a team to take more shots and try to push play in the offensive zone in order to score more goals? Or, is blocking opponents’ shots a better approach to winning a game? The overall scheme for the season could also be considered. If a coach teaches an aggressive style of play that scores a lot of goals, but also gives up more goals, will that lead to a better record at the end of the season than one that preaches defense?
3.1. Seasonal Analysis
In this part of the research, we examined what components were most important to the overall seasonal success of a team, namely to the team making the playoffs. Twenty-four initial variables were selected and their seasonal values for each of the thirty teams for each of the seven seasons (2005-06 through 2011-12) were accessed from the NHL website [6]. Some of the variables considered included total goals scored for the season, total goals scored against for the season, total shots for the team, total shots against the team, total penalty minutes, among others. There were 210 observations for each variable. A complete list of all the variables considered is given in Table 1.| Table 1. List of Initial Seasonal Variables |
| | Blocked shots | Save percentage | Faceoff win percentage | Shot plus/minus | | Five on five goals/goals against ratio | Shots against | Giveaways | Shots for | | Goal plus/minus | Takeaways | Goals | Winning percentage when leading after 1st period | | Hits | Winning percentage when leading after 2nd period | Missed shots | Winning percentage when outshooting opponent | | Penalty kill percentage | Penalty minutes | Power play goals | Winning percentage when outshot by opponent | | Power play goals against | Winning percentage when scoring first | Power play percentage | Winning percentage when trailing first |
|
|
A stepwise discriminant analysis was used to determine which variables were most important in predicting whether or not a team made the playoffs. If a team made the playoffs, this was recorded as a “1”. A “0” was recorded if a team did not make the playoffs. The selection criterion chosen was an entry alpha level of 0.25 for a variable, and a significance level of 0.20 to stay in the model. The order and degree of influence each variable has for a team making the playoffs was determined.Classification analysis was next performed on the data to determine how well the variables that were selected actually worked at classifying teams as to whether or not they made the playoffs. A prior probability of 0.5333 (16/30) was assigned a team of making the playoffs and 0.4667 of a team to not make the playoffs since it is known that 16 of the 30 teams make the playoffs each year.
3.2. Game Analysis
In this aspect of the research, models to predict the winner of a future hockey game were formed by estimating the probability that a given team will win the game, and then by estimating the difference in the number of goals scored between two teams in a game. These models also helped us determine which factors have the most influence on a team winning the hockey game.Initially data for sixty variables was collected from individual games during the 2009-10 season and the 2010-11 season. This initial set of game variables is given in Table 2. We decided to divide each season into four quarters to ensure an even sampling of the games. Quarter 1 included games 1 through 20; Quarter 2 games 21-40; Quarter 3 games 41-60; and Quarter 4 games 61-80. We sampled one game from every team for each quarter for both years. This resulted in eight total games for each team, or 240 total observations. The games were selected for each quarter using a 1-in-k systematic approach. Namely, a random number from 1 to 20 was chosen for each season and that game of each quarter was selected. For the 2009-10 season, the random number generated was 16. Therefore, values of the variables for the 16th, 36th, 56th, and 76th games were collected for each team. In the event that this system selected the same game for two different teams, the first game prior to the selected game was used for the later team. If this game had already been selected, the first game prior to this game was selected. For the 2010-11 season, the random number 5 was generated, resulting in the 5th, 25th, 45th, and 65th games used to gather data for the teams. All the statistics were gathered from the website, www.NHL.com [6].A logistic regression model was first developed to estimate the probability the “team of interest” would win the game. In this case, the dependent variable was set equal to “1” if the team won the game (or it was tied at the end of regulation) and “0” if the team lost the game. The stepwise selection technique was used to help develop the model with the variables under consideration given in Table 2. For this model, we initially set the alpha level of entry to 0.25 for a variable to enter the model and the alpha level to stay was set to 0.20. | Table 2. List of Initial Game Variables |
| | Assist margin | First goal scored | Assists | Giveaway margin | | Assists against | Giveaways | Block margin | Goal margin | | Blocks | Goals | Down 1 goals against | Goals against | | Down 2 goals against | Hits | Even=handed faceoff win percentage | Hits margin | | Even-handed goal margin | Missed shot margin | Even-handed goals | Missed shots | | Even-handed goals against | Opponent Blocks | Even-handed shot margin | Opponent even-handed shots | | Even-handed shots | Opponent giveaways | Faceoff losses | Opponent hits | | Faceoff win percentage | Opponent Missed shots | Faceoff wins | Opponent power play shots | | Opponent save percentage | Second goal scored | Opponent short-handed shots | Short-handed faceoff win percentage | | Opponent takeaways | Short-handed goals | Penalty kill percentage | Short-handed goals against | | Penalty minutes | Short-handed shot margin | Power play faceoff win percentage | Short-handed shots | | Power play goal margin | Shot margin | Power play goals | Shots against | | Power play goals against | Shots for | Power play percentage | Takeaway margin | | Power play shot margin | Takeaways | Power play shots | Time on power play | | Power play time margin | Up 1 goals | Save Percentage and Margin | Up 2 goals |
|
|
The second model developed was to estimate the difference between the number of goals scored by the “team of interest” and the “opposing team”. The stepwise technique using ordinary least squares regression was used to help develop possible models with the list of variables under consideration given in Table 2 and an initial alpha level of entry equal to 0.25 and alpha level of stay equal to 0.20. In this case, the dependent variable was the difference between the number of goals made by the “team of interest” and the “opposing team”. A final model was developed based on comparing the R-squared values of models as variables entered into each of the models and by considering the simplicity of the models.Once a final model was selected for estimating the probability that the “team of interest” would win the game and a final model was also selected for estimating the difference in the number of goals scored between the “team of interest” and the “opposing team, a second data set was then collected in order to validate the models. Games were selected from the 2011-12 season, outside the timeline for the original data set the models were based on. This was done by randomly selecting a number between 1 and 40 (first half of the season) and then randomly selecting a number between 41 and 80 (second half of the season). The numbers 23 and 48 were selected implying games 23 and 48 for each team were included in the sample of sixty games. If both of the models are good models, then when the actual game values for the variables are known, the models should do well at determining which team won the game and what the actual point spread of the game was.Finally, a third data set was collected to test the predictability of the models. To do this, sixty games were randomly selected from the 2011-12 season including games 4 and above for all teams. The actual in-game data values were not used for the variables in the model. Instead of using these actual values, averages of the values of the variables in the model for the previous three games were calculated and these averages were placed in the models. This was done to see if the models could predict what would happen in the game based on both teams’ performances in the previous three games. The results obtained at this stage were compared to common benchmarks for prediction.
4. Results
4.1. Seasonal Analysis
Results from the seasonal data using the stepwise discriminant method shows that the most influential seasonal factors contributing to a team making the playoffs are total goals given up for the season, total goals scored for the season, and the total number of takeaways for the season. Table 3 shows the stepwise selection process along with the partial R-squared values associated with each of the variables.| Table 3. Stepwise Selection for Seasonal Model |
| | Step | Variable Entered | Partial R2 | F-value | Pr>F | | 1 | Goals Against | 0.365 | 119.77 | <0.0001 | | 2 | Goals | 0.305 | 90.64 | <0.0001 | | 3 | Takeaways | 0.018 | 3.74 | 0.055 |
|
|
From the subset selection procedure, we can now look at the linear discriminant functions for making and not making the playoffs based on the standardized variables. The results are given in Table 4. As you can see in both cases, the magnitude of scoring goals is less than that of allowing goals. This would lead us to believe that it is more important to give up fewer goals than it is to score an abundance of them in order to make the playoffs. Takeaways are not as important as the two goal statistics. | Table 4. Linear Discriminant Functions |
| | Variable | Did Not Make Playoffs | Made Playoffs | | Constant | -1.502 | -1.195 | | Goals Scored | -1.060 | 0.927 | | Goals Against | 1.510 | -1.321 | | Takeaways | -0.220 | 0.192 |
|
|
A classification analysis was performed to see how well the data can be grouped using our significant factors and their discriminant functions. The holdout procedure was used to refit the model with each observation being classified using all remaining observations excluding itself. Prior probabilities were used as mentioned in Section 3 and given again in Table 5. The error rates for classification are given in Table 5 with a misclassification rate of 0.129. Therefore, 87.1% of the time, a team was correctly classified as a playoff team or a non-playoff team. It is noted that only 8.9% of the teams were classified as not making the playoffs when they actually did and 17.4% of the teams were classified as making the playoffs when they actually did not.| Table 5. Crossvalidation Classification Table |
| | Playoffs & Prediction | Did Not Make Playoffs | Made Playoffs | Total | | Predicted to Not Make Playoffs | 81 | 10 | 91 | | Predicted to Make Playoffs | 17 | 102 | 119 | | Total | 98 | 112 | 210 | | Error Rate | 0.174 | 0.089 | 0.129 | | Prior Probability | 0.467 | 0.533 | |
|
|
4.2. Game Analysis- Using Logistic Regression
We will first examine the results from the logistic regression model which was developed to estimate the probability of a given team winning the game. There were 62 initial variables considered for entry into the regression model and these are given in Table 2. Stepwise logistic regression was performed resulting in a model with eight significant variables: save percentage margin, shot margin, even strength faceoff percentage, short-handed faceoff percentage, block margin, short-handed shot margin, power play time margin, and giveaway margin. The intercept term was found to not be significantly different than zero, and was therefore set to zero. This makes sense because if the values of the variables for both teams were equal, the probability of either team winning the game would equal 0.50 which would only be the case if the intercept was zero. In the stepwise regression technique, we initially used an alpha value of 0.20 for a variable of staying in the model. Two of the p-values for the eight variables in the initial model were higher than 0.06 and were taken out of the model. These variables were power play time margin and giveaway margin. The final model used contained the remaining six variables. A Hosmer-Lemeshow test was conducted on the final model testing for whether the logistic model was a good fit. The p-value associated with this test was 0.943 implying that there is no evidence that the logistic model is not appropriate. The receiving operating characteristic curve for this model had an area of 0.989 under the curve indicating that there are few false negatives and many true positives. Therefore, when the actual variable values for the game were known, the model had very few cases in which it indicated a win when the team did not win and many cases in which it indicated a win and the team did win. The parameter estimates associated with each of the variables in the logistic model, along with their odds ratios are given in Table 6.| Table 6. Parameter Estimates and Odds Ratios |
| | Variable | Parameter Estimate | Standard Error | Odds Ratio Estimate | | Save Percentage Margin | 0.836 | 0.148 | 2.306 | | Shot Margin | 0.269 | 0.051 | 1.309 | | Block Margin | 0.151 | 0.057 | 1.163 | | Short-handed Faceoff Percentage | 0.044 | 0.016 | 1.045 | | Short-handed Shot Margin | -0.481 | 0.207 | 0.618 | | Even-handed Faceoff Percentage | -0.033 | 0.016 | 0.968 |
|
|
We next wanted to validate our model. Sixty games were selected from the 2011-12 season. Fifty-two games from this set were actually used since eight of these 60 games were decided in a shootout. Shootout games occur when there is a tie after the original 60 minutes of play and after 5 minutes of sudden death overtime. Since shootouts do not consist of team play and only one-on-one situations between player and goalie, these games were not considered. The actual values of the in-game statistics were placed into the model for these fifty-two games in the order of “team of interest” minus “opposing team”. If the model gave a probability of 0.50 or higher when the actual in-game statistics were entered from the game, we would expect the “team of interest” to win or tie the game. Otherwise, we would expect the “team of interest” to lose the game. Fifty-one out of fifty-two games were correctly decided using the model with using the actual in-game values for the six variables. The model is validated since it did work well for another sample that was not used in the model derivation when the actual in-game values of the variables are known.The next step was to try and predict the outcome of games that have not yet occurred. To do this, we considered the averages of the in-game values (for the six variables in the model) from the previous three games prior to the game of interest for both teams.Sixty games were randomly selected from the 2011-2012 season beginning with game 4 for each team using a systematic sampling approach. Three games averages for each of the variables in the model based on the last 3 games played for each of the teams involved in the game were calculated. These values were entered into the model in the order of “team of interest” minus “opposing team”. If the estimated probability of winning the game for the “team of interest” was greater than 0.50, we predicted that the “team of interest” would win or tie. If this estimated probability was less than 0.50, we predicted that the “team of interest” would lose the game.Shootout wins and losses in these cases were considered in the same class as wins. Losses were only deemed a loss if the team was defeated during regulation time or overtime. It was determine that 39 out 60 games were correctly predicted, or the model had a success rate of about 65%. We compared this success rate with three basic scenarios as to how we could predict the winner of a hockey game. These scenarios included the following: always choosing the home team; always choosing the team with the better record; and finally by always choosing the higher rated team on the sports handicapper website covers.com. The home team has won about 55% of the time over the last five seasons. Choosing the team with the better record also had a success rate of 55%. A one-sample test of proportion was conducted comparing the 55% correct rate to our 65% correct rate. The 65% correct rate is significantly higher than a 55% correct rate based on a p-value of 0.052. From the historical handicapping data given on the website covers.com, it only correctly predicted a winner 52% of the time. A success rate of 65% is significantly higher than the 52% based on a p-value of 0.013. Namely, this model significantly predicted more hockey games correctly than always selecting the home team, or always selecting the team with the better record, or always selecting the better team based on the handicapper website.
4.3. Goal Margin Model
Least squares regression was used in the second model derived to estimate the actual goal margin at the end of the game. The stepwise regression technique was employed considering the same 62 initial game variables (Table 2) as with the logistic regression technique. The alpha value for entry was set equal to 0.25, and the alpha value to stay was set equal to 0.20. The initial results are given in Table 7. There were seven variables included in the initial model, but five of these variables had partial R-squares less than 0.002 with two of the five variables having p-values greater than 0.06. We elected to take these five variables out of the model. The final model that we used is given in Table 8. The intercept was not significant with a p-value of 0.364, and was therefore set to zero. This should be expected since if the values of the variables in the model for both teams are the same, one should expect the goal margin to be zero. The final model has an adjusted R-squared value of 0.931. | Table 7. Stepwise Selection for Goal Margin Model |
| | Step | Variable Entered | Partial R2 | F-value | Pr>F | | 1 | Save Percentage Margin | 0.820 | 1018.71 | <0.0001 | | 2 | Shot Margin | 0.116 | 405.15 | <0.0001 | | 3 | Power Play Goal Margin | 0.002 | 6.87 | 0.009 | | 4 | Even Shot Margin | 0.002 | 5.88 | 0.016 | | 5 | Hits Margin | 0.001 | 3.89 | 0.050 | | 6 | Power Play Time Margin | 0.001 | 3.29 | 0.071 | | 7 | Missed Shot Margin | 0.001 | 2.64 | 0.106 |
|
|
| Table 8. Parameter Estimates for Goal Margin Model |
| | Variable | Parameter Estimate | Standard Error | | Save Percentage Margin | 0.271 | 0.005 | | Shot Margin | 0.090 | 0.005 |
|
|
In order to validate the goal margin model, we considered the same 60 games sampled from the 2011-12 season which were used in validating the logistic model. These games were not used in the development of the model. The in-game values for the two variables in the goal margin model were put into the model. If the model results in a value greater than zero, the model is indicating that the “team of interest” will win the game. If the model results in a value less than zero, the model is indicating that the “team of interest” will lose the game. Shootout games were eliminated from consideration resulting in 52 games remaining. Of these 52 games remaining, the model did get all 52 games correct as far as determining which team won the game by knowing the save percentage margin and shot margin for the teams playing, The model only missed the actual goal margin by an average of 0.43 goals per game. The model is validated since it did work well for another sample that was not used in the model derivation when the actual in-game values of the variables are known.The predictive ability of this model was tested using the same 60 games that were used to test the predictive ability of the logistic model. The three games prior averages were taken for save percentage and shots for each team. Shootout games were grouped with wins. Forty out of the sixty games, or 66.7%, of the games were correctly predicted. This is slightly better than what we got for the logistic model and significantly better than selecting winners based off of selecting the team playing at home, selecting the team with the better record, or by selecting the team selected by the handicapping website [7]. The goal margin model did well at selecting a winner, but it was not very accurate when considering what the final goal margin of the game actually was.
5. Conclusions
The goal of this research was not to just be able to predict the outcome of ice hockey games, but rather to get a better understanding of the factors that contribute towards winning. If you look at what significant variables were used to determine whether a team was successful over the course of an entire season and made the playoffs, you see that goals scored, goals against, and takeaways are the three most important factors. The determinant function indicates that goals against has a larger magnitude than goals scored. This would lead us to believe that it is more important for the team that is striving to make the postseason to keep their opponents from scoring an abundance of goals. It boils down to a comparison of strategies, a strong defensive team that may not score a lot of goals may have an advantage in making the playoffs over a team that has a lot of offensive capabilities, but is lacking a good defensive scheme. Scoring goals is still important obviously because that is how you win, but the evidence suggests that over the long course of a season, preventing scoring is more vital. In addition to this, the fact that takeaways are important in determining who will win the hockey games gives even further evidence that defense is more crucial than offense. Even over the short term, defense shows it has a larger impact than offense. When trying to predict the winner of an individual game based on the logistic model, the most important factor in the model is save percentage. For every percentage point better your team is at stopping the shots, the odds of winning get multiplied by 2.3 (Table 6). Shots are important because they eventually lead to goals, but not to the same degree as stopping shots. It is also noted, that in the logistic regression model, short-handed faceoff percentage difference was included in the model, but the difference in power play faceoff win percentages was not. Power plays generally lead to more scoring especially if you can control the puck [8]. However, when a team is short-handed they rarely score any goals and winning possession of the puck off of a faceoff is even more critical in order to keep the opponent from setting up plays. Again, it is seen here that defense is more important.Furthermore, when you look at the goal margin model, save percentage margin has a larger influence than shot margin. This is a further indication that defense has more weight than offense in winning a hockey game.There are many times a franchise will have to choose between trying to sign different free agents. A flashy player that can score a lot of goals certainly seems tempting to have on your team, but could an average player who is much better at defense be a better choice? Maybe the offensive player is so good he overcomes any deficits in defense, but perhaps the average player is a better choice if he stops more goals, and would not demand as much money as a superstar player.
References
| [1] | Ryder, Alan [2004a]. “Win Probabilities: A tour through win probability models for hockey”. [Online] Available: http://www.hockeyanalytics.com. |
| [2] | Ryder, Alan. [2004b]. “Poisson Toolbox: A review of the application of the Poisson Probability Distribution in hockey’. [Online]. Available: http://www.hockeyanalytics. |
| [3] | Thomas, Andrew C. [2007]. Inter-arrival Times of Goals in Ice Hockey, Journal of Quantitative Analysis in Sports, Vol.3, Issue 3, Article 5. |
| [4] | Thomas, Andrew C. [2006]. The Impact of Puck Possession and Location on Ice Hockey Strategy, Journal of Quantitative Analysis in Sports, Vol. 2, Issue 1, Article 6. |
| [5] | Moskowitz, Tobias, & Wertheim, Jon. L. [2012]. Scorecasting: The Hidden Influences Behind How Sports Are Played and Games Are Won. Crown Publishing Group. |
| [6] | NHL Scores [2005-2012]. [Online] Available: http://www.nhl.com/ice/scores. |
| [7] | Sports website [Online]. http://www.covers.com. |
| [8] | Jones, Joe. [2012]. “The Importance of Faceoffs. Seeing the Ice” [Online] Available:http://www.seeingtheice.wordpressocom. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML