-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Sports Science
p-ISSN: 2169-8759 e-ISSN: 2169-8791
2013; 3(2): 37-45
doi:10.5923/j.sports.20130302.01
Fundamentals of SCUBA-Diving Physics
Achim M. Loske
Centro de Física Aplicada y Tecnología Avanzada, Universidad Nacional Autónoma de México, Querétaro, Qro., 76230, México
Correspondence to: Achim M. Loske, Centro de Física Aplicada y Tecnología Avanzada, Universidad Nacional Autónoma de México, Querétaro, Qro., 76230, México.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Diving with an underwater breathing apparatus has been the subject of research in several scientific areas for a long time. Decompression and recompression are complex and involve knowledge of physics and physiology. The purpose of this article was to review the basic physics of autonomous diving and to describe phenomena not so obvious to scientists working in other fields. Special emphasis was given to the effects of breathing pressurized air. Some effects of hydrostatic pressure on our body, nitrogen narcosis, oxygen toxicity, decompression sickness and other topics related to SCUBA diving are discussed from the standpoint of physics. The basic principles of dive tables and no decompression limits are also explained.
Keywords: SCUBA-diving physics, Partial pressure of a gas, Decompression tables, Combined gas law, Mixture of gases
Cite this paper: Achim M. Loske, Fundamentals of SCUBA-Diving Physics, International Journal of Sports Science, Vol. 3 No. 2, 2013, pp. 37-45. doi: 10.5923/j.sports.20130302.01.
Article Outline
1. Introduction
- Autonomous diving, also known as SCUBA (Self Contained Underwater Breathing Apparatus) diving, was developed in the 40’s. When mentioning the term SCUBA, in general an open circuit equipment is meant, although this term also comprises closed circuit equipments with re-inhalation, which use carbon dioxide filters. Despite the fact that diving with a pressurized air tank has been the subject of study for more than seventy years, there are still unknown aspects about it. Techniques, equipment and safety measures are constantly modified, and the physics and physiology of diving are still topics for research. The purpose of this article is to describe the basic principles related to the physics of autonomous diving.During the Renaissance, the idea of building submarines captured the imagination of wise men such as Leonardo da Vinci and Borelli; however their designs failed due to the technical limitations of their time. Because of that, it was necessary to turn to bathyspheres. One of these bathyspheres, made of wood, and equipped with glass windows and skin hoses to provide fresh air to the diver was patented by the famous astronomer Edmund Halley. In 1866, Rouquayrol designed a pressure gauge for an air breathing device, but then again, the technology of that time didn’t allow it to be built. A significant advance was achieved in 1942 by the French Navy Officer Jacques-Yves Cousteau who, along with engineer Emile Gagnan, invented the so called aqualung system, based on the compressed-air device of Captain Yves Le Prieur and the previously mentioned pressure gauge, designed by Rouquayrol and Denayrouze.Some of the fundamental laws that govern SCUBA - diving physics are:a) Archimedes' principle: the weight of the diver and his equipment, and the weight of the volume of displaced water determine whether the diver will float or sink.b) Snell's law: the diver sees objects closer and larger than they are, because the refraction indexes of water and air are different.c) Boyle's law: as pressure changes, the volume of gases in the diver's body and soft equipment varies.d) Gay-Lussac's (Charles) law: if the temperature changes, the pressure inside the diving tank varies.e) Dalton's law: the concentration of each component of the air breathed by the diver can be determined by its partial pressure.f) Henry's law: gas absorption by the tissues of the human body is proportional to the partial pressure of the gas.The laws of thermodynamics related to heat loss and other aspects of diving could also be included in this list; however, the purpose of this article is to describe phenomena that are characteristic of SCUBA diving and not obvious for scientists working in other fields. Special emphasis will be given to the effects of breathing pressurized air. Nitrogen narcosis, oxygen toxicity, and decompression sickness are discussed from the standpoint of physics. Some fundamentals of dive tables and no decompression limits are also described.
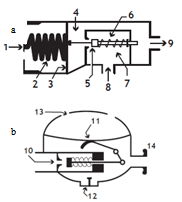
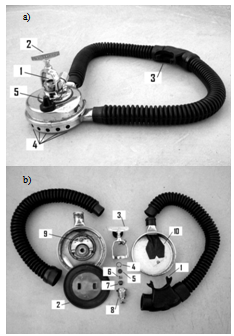
2. The Autonomous Compressed Air Equipment
3. Phenomena Associated to Hydrostatic Pressure and Breathing of Gases under Pressure
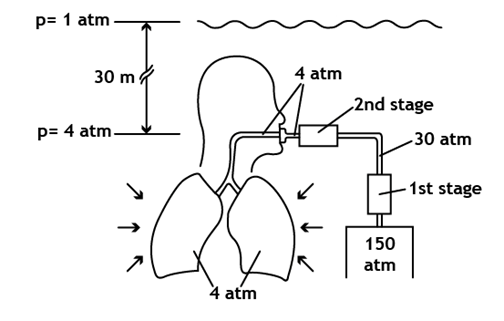
- At sea level, the weight of the atmosphere exerts a pressure of 14.7 psi (1 atm) onto our body, i.e., a column with a base of one squared inch and a height equivalent to the Earth’s entire atmosphere weighs 14.7 pounds. Since our body is adapted to such pressure, we practically don’t feel it; however, we are able to perceive slight pressure changes. During the breathing process, oxygen is absorbed by the blood and carried to all cells in our body, which use it for their metabolism, producing carbon dioxide. Oxygen is important for transforming nutrients into energy, but it is toxic if breathed at a pressure above a certain limit. On the other hand, carbon dioxide is eliminated through the same way, but in the opposite direction. Since the air current in our airways is turbulent, when the density of the breathed air increases, so increases the resistance of its flow through the airways.
3.1. Partial Gas Pressure
- In order to describe the behavior of a mixture of gases, such as air, it is advisable to remember the model proposed in 1801 by John Dalton, as well as the model of the physicist Emilie Hilarie Amagat[4]. Before Dalton published his works on atomic theory, most of the scientists believed that atoms of any kind of matter were equal among them. His theory established that the atoms of each element were different in mass and size, and that in a mixture of gases; only equal atoms interacted with each other. Even if it was finally demonstrated that the latter was false; it allowed Dalton to explain why, within a mixture, a gas in a container behaves as if the other gases didn’t exist.Suppose that the air within a diving tank is composed by gases whose masses are m1, m2, m3, etc.; therefore, the total mass of air is the sum of the masses of the composing gases:
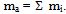 | (1) |
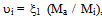 | (2) |
|
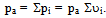 | (3) |
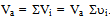 | (4) |
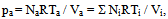 | (5) |
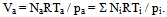 | (6) |
3.2. Intoxication for Breathing Pressurized Gases
- Most of the gases cause a general loss of senses when breathed at high partial pressures[1]. Holding the breath in order to get a higher yield of the diving tank may cause intoxication due to carbon dioxide. If the level of carbon dioxide reaches 10%, the diver loses consciousness. On the other hand, while descending with the described equipment at depths below 30 meters, the diver may suffer nitrogen narcosis[6-8]. This is shown as an excess of confidence and loss of judgment, causing a sensation similar to inebriation. Nitrogen narcosis is a reversible alteration of the nervous system, caused by breathing nitrogen at a high partial pressure. Fortunately, it is not addictive nor does it have secondary effects. It is believed that nitrogen alters the electric transmission between neurons; however, the aspects of the mechanism that triggers such alteration are still unknown.The partial pressure of oxygen (ppO2) and nitrogen (ppN2) at sea level are about 0.21 atm and 0.78 atm, respectively. As the diver descends, the total pressure of the inhaled air increases, and so do the partial pressures of the gases composing the gas mixture. When the diver is 40 meters deep, he is breathing air at 5 atm, and the partial pressures of oxygen and nitrogen reach 1.05 atm and 3.9 atm, respectively. A partial pressure of about 4 atm is the limit for nitrogen narcosis[1],[6],[7]. This limit depends on each person, and even for the same person, it may vary from one day to the other. If a diver suffering nitrogen narcosis is slowly taken to more shallow waters, the symptoms disappear. Because of this, immersions deeper than 40 meters should be done using a gas mixture different from that of air. Regardless of nitrogen narcosis, diving with compressed air below 40 meters turns out to be dangerous due to oxygen intoxication. This phenomenon, referred to as the Paul Bert effect happens as a result of breathing oxygen at a high partial pressure[8-12]. Oxygen intoxication, whose symptoms are nausea, blurry vision, confusion, convulsions and unconsciousness may appear at 43 meters in depth. Differently from what many people believe, sports SCUBA diving tanks do not carry pure oxygen. The U.S. Navy establishes that 25 feet deep (about 7.6 m) is the maximum limit to dive with a tank that contains 100% oxygen. At this depth, the ppO2 equals 1.76 atm.
3.3. Shallow Water Blackout
- The so-called “shallow water blackout” which may happen while free diving, is related to Dalton’s law. Our brain has an amazing control over breathing, formed by chemical receptors that detect the percentages of oxygen and carbon dioxide diluted in the blood that comes from the lungs. Hypercapnia is an excess of carbon dioxide in the body, and may be due to poor lung ventilation or to a great physical effort. A high content of carbon dioxide produces the stimuli to breath. On the other hand, hypocapnia is the lack of carbon dioxide. At normal conditions, the percentage of inhaled and exhaled carbon dioxide is 0.03% and 5.6%, respectively. Fainting may occur after a hyperventilation. If a diver hyperventilates, reducing his level of carbon dioxide, and then dives into an apnea, at let’s say, 10 meters deep, the ppO2 reaches 0.42 atm. The organism will be consuming oxygen at a higher partial pressure, and since the carbon dioxide was reduced because of hyperventilation, the diver does not feel the need to breath. After some time, during which oxygen is still being consumed, carbon dioxide reaches a level where it excites the breathing system, and the diver feels the need to breathe, so he starts to ascend. Upon staring the ascent, the level of oxygen is low, and as the diver tries to reach the surface, hydrostatic pressure diminishes, allowing the expansion of the lungs. Therefore, the ppO2 may reach the lowest bearable limit of 0.1 atm, causing the loss of consciousness.
3.4. Gas Diffusion
- Between the molecules of a liquid, there is free room for gas molecules. The pressure exerted by these gas molecules onto the liquid is known as gaseous pressure. The pressure gradient between the partial pressure of the gas in contact with the liquid and the gaseous pressure within the liquid is proportional to the gas absorption of the liquid. This ingassing process is reversed when the partial pressure of the gas in contact with the liquid is lower than the gaseous pressure (outgassing). When a gas is in contact with a liquid, a certain number of gas molecules diffuse into the liquid, until there is a balance between the non dissolved gas and the one dissolved in the liquid. The balance constant for this case is:
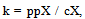 | (7) |
3.5. The Ascent
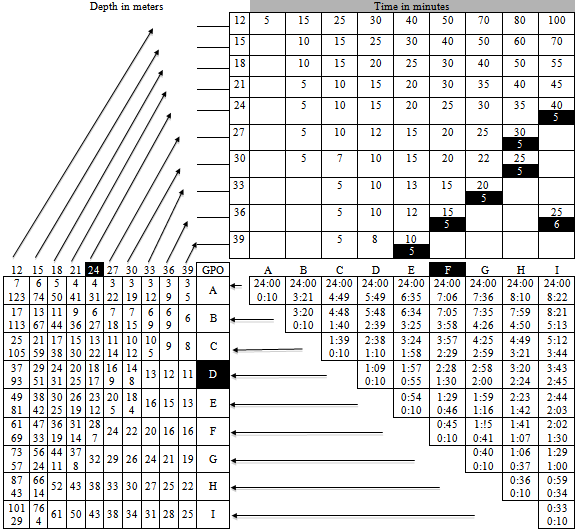
- During ascent, the external pressure exerted onto the body is reduced. If the accent is slow, the dissolved gas will diffuse back from the bloodstream to the lungs and will be exhaled. However, if the diver ascends too quickly, it is very likely that nitrogen bubbles will form within the blood stream. The formation of bubbles in the organism is known as decompression accident, gaseous stroke or bends and is caused by a brisk pressure reduction[6]. Bubbles may block the bloodstream, causing ischemic symptoms in different areas of the brain, kidneys and other organs. Some of its symptoms are acute pain in certain parts of the body, partial or total paralysis, permanent injuries and death[1],[2].Since oxygen and carbon dioxide pass quickly to their soluble state into the blood, bubbles are generally composed by nitrogen. Nitrogen is a non-metabolic gas, i.e., it is not consumed by the body. The bubbles of this gas do not disappear, unless the diver is subject to pressure again, in this case, inside a hyperbaric chamber, in order to slowly reduce the pressure, allowing the exhalation of nitrogen through the lungs. It is important to mention that upon increasing the volume of bubbles, their internal pressure decreases favoring the diffusion of more gas into the bubble, that is, the increase in volume of these bubbles is not caused exclusively by Boyle’s law.In order to prevent the formation of bubbles within the organism, divers must ascend at a speed equal or lower than one foot per second. If they remain at a depth of more than 10 meters for a time that is longer than a certain limit (which depends on the depth), ascending slowly will not be enough, and one or more decompression stops, at known depths will be necessary before returning to the surface.The basis for decompression charts were set in 1908 by the physiologist John Scott Haldane. Decompression sickness affected not only divers but also caisson workers in tunnels. According to his theory, nitrogen absorption and elimination in tissues follows an exponential pattern[1],[6]. Haldane’s principle establishes that there won’t be any formation of bubbles in the organism unless pressure is suddenly reduced to half its value. Thanks to the use of Doppler ultrasound equipment, it is now known that, contrary to what Haldane proposed, asymptomatic micro-bubbles can be formed, even when following the limits of no-decompression.The diving charts of the National Association of Underwater Instructors (NAUI)[3] require a diver who has been for, let’s say 40 minutes at a depth of 30 meters, to make a decompression stop of 15 minutes at 5 meters, therefore, his total ascent time should not be less than 15 minutes, plus one minute and 40 seconds. In the case of repetitive diving, the allowed times are reduced according to the depth and time of the first dive of the day, since it has to be taken into account that an excess amount of nitrogen remains in the body for several hours. The NAUI proposed a model called reduced gradient bubble model according to which, any immersion that exceeds 12 meters of depth should include a decompression stop of one minute at half the maximum depth. This model has been incorporated into diving computers.In addition to looking out for the speed of ascent, the diver should continue breathing normally since otherwise he may suffer a lung rupture. If he holds his breath during ascent, the volume of air inside the lungs increases, due to the constant reduction of hydrostatic pressure, an there may come a moment when the difference between the pressure inside the lungs and hydrostatic pressure is so big that the lungs cannot resist it.Fortunately, advances in electronics have led to the development of reliable portable diving computers. At all times, they show the depth, the diving time, the maximum depth reached, the depths and times of decompression stops, the total time for ascent, the time on the surface needed to eliminate remaining nitrogen from his organism, the minimum time the diver has to wait before taking a plane, the speed of ascent, the pressure of the air contained in the scuba tank, the remaining diving time, etcetera. These computers also have visual and auditory alarms to warn the diver should he skip one of the decompression stops or if his breathing rate is too fast. The algorithm considers water temperature and the effort made by the diver under the water. Once at the surface, the computer may be connected to a PC via an interphase, in order to analyze the most important parameters of the last dives. In case of doubts, skipped decompression stops, high speed accents, accidents or any other kind of anomalies, the software provides relevant data for the treatment of the diver in a hyperbaric chamber. The use of dive computers increases security and allows for longer immersions. The latter is because, as it is described later on, diving charts only consider the maximum reached depth, regardless of the time spent at such depth. In fact, these charts were calculated considering that the diver was at the same depth during all the dive time, that is, the diving chart is considered to be “rectangular”. Diving computers update all of these calculations several times per second.
4. Decompression Tables and Algorithms
|
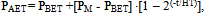 | (8) |
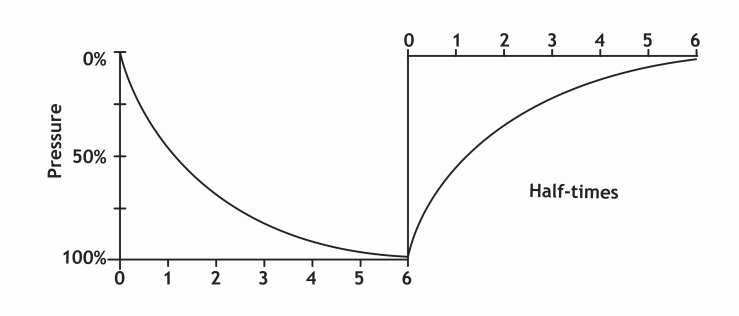 | Figure 5. Graph of nitrogen ingassing and outgassing in a specific tissue |
5. Diving with a Mixture of Gases
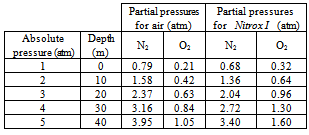
- In some cases, it is necessary to dive using a mixture of gases different from air[13]. Its use demands special algorithms. Mixtures of gases are used for deeper dives than the ones previously mentioned, or when it is needed to remain under pressure for longer periods without suffering the consequences of nitrogen narcosis or oxygen intoxication. As it was previously mentioned, the minimal ppO2 that the human body requires is 0.1 atm. A lower partial pressure may cause death. Although 0.21 atm is the ppO2 at which our organism is accustomed, a healthy diver may be sufficiently oxygenated at a ppO2 of only 0.16 atm. On the other hand, as already mentioned, breathing oxygen at a pressure higher than 2 atm may cause oxygen intoxication[10]. The moment when the symptoms appear depends on the time the diver breathed oxygen at this partial pressure. After many years of theoretical and practical studies, the U.S. Navy and other research centers in different parts of the world, determined the maximum ppO2 a diver may breathe during a certain time without suffering any disturbances. For example, it is allowed to breathe oxygen at a partial pressure of 1.0 atm for 140 minutes; however, at 1.6 atm, the time limit is only 30 minutes.A mixture of gases that was originally used only for industrial diving, and then was adopted by sport divers is known as Nitrox I, also referred to as Enriched Air Nitrox (EAN), which is 32% oxygen and 68% nitrogen. Diving with this type of mixture alters the decompression algorithms previously mentioned. Breathing Nitrox I at 30 meters of depth implies a ppN2 of 2.72 atm (4 atm × 0.68). The same ppN2 exists when breathing air at about 24 meters of depth. This means that, as for inhaled nitrogen, it is the same to dive at 24 meters of depth with compressed air as it is to dive at 30 meters of depth with Nitrox I. This example would give around 15 additional minutes as the limit time of decompression when using Nitrox I. Table 4 shows partial pressures of nitrogen and oxygen for air (considering that air is composed only by nitrogen and oxygen) and Nitrox I at 5 different pressures (depths). It can be seen that at an absolute pressure of 4 atm, equivalent to a depth of 30 meters, the ppO2 for a diver breathing Nitrox I is 1.3 atm. The limit time to breathe oxygen at this partial pressure without suffering consequences is 60 minutes. The ppO2 breathing air at this depth is only 0.84 atm. To sum up, the higher the oxygen in the mixture of gases breathed, the lower the depth that may be reached. An advantage of Nitrox is the lower percentage of nitrogen.Nitrox II is composed by 36% oxygen and 64% nitrogen. At any depth, whether breathing air or Nitrox, both nitrogen narcosis and oxygen intoxication should be considered. An additional advantage of breathing Nitrox instead of air is that the diver feels less fatigue. Despite this, the use of Nitrox is not as common as the use of compressed air, mostly because, due to the higher content of oxygen, it is flammable, and should be handled with care.Nitrogen narcosis may be avoided by completely eliminating nitrogen in the mixture of gases, and breathing a lighter gas, such as helium, that is, filling the tank with a mixture of helium and oxygen (Heliox). During the sixties, Keller and Bühlmann created new methods for diving with this type of air mixtures, allowing deeper immersions. This is possible because our organism does not need nitrogen for its metabolism. Using Heliox it is possible to go at depths beyond 60 meters. An additional advantage of helium is that it may be quickly eliminated by the organism. Because of its cost, Heliox is not common in sport diving. In addition, it must be remembered that the time for decompression stops is a function not only of the inert gas, but also of depth, time of immersion and the ppO2. Another disadvantage of helium is that its thermal conductivity is much higher than that of air. This generates a considerable loss of heat in every exhalation, so it is necessary to heat up the gas before it is breathed. For industrial diving, there are semi-closed circuit equipments that filter and reuse certain amount of the exhaled gases, in order to reduce the consumption of helium. Trimix, is another common mixture, composed by oxygen, helium and nitrogen. It is used in several proportions, depending on the depth to be reached. By definition, the mixture is presented by the percentage of oxygen, followed by the percentage of helium, being understood that the remaining percentage, to reach 100% should be nitrogen. So, in a 10/70 Trimix mixture, there is 10% oxygen, 70% helium and 20 % nitrogen. Such mixture is adequate for immersions up to 100 meters. The limit depth and maximum immersion time are obtained by considering a ppO2 between 1.0 and 1.2 atm. For deep diving, several mixtures of gases are used. Upon descending, the percentage of O2, is reduced, until a “bottom mixture” is reached. For returning back to the surface, a “travel mixture” is used, where the content of oxygen is increased as the diver ascends.
|
6. High Altitude Diving
- Decompression algorithms should be adjusted when not diving at sea level, since it has to be taken into account that atmospheric pressure varies with altitude. The time the diver has been at a certain altitude before diving must also be considered. If coming from a place of a lower altitude, the diver already has some “residual” nitrogen, even without having dived. So, for example, a diver who travels from sea level to a place that is at an altitude of 3000 ft (about 914 m), must consider a “C” repetition group (see Table 2) before diving. By introducing a correction factor, previously determined for each altitude, it is possible to use those decompression tables designed for diving at sea level. In addition, the speed at which the diver ascends to the surface in a lake above sea level should be below the 60 ft/min that are customary at sea level. Such speed is inversely proportional to the altitude of the site for diving. At an altitude of 14,000 ft (around 4,260 m), the velocity of ascent should only be of about 36 ft/min.
7. Conclusions
- Breathing gases under pressure produces significant physiological changes. Although in the beginning the main problem for diving was thought to be the air supply, it was soon discovered that this had a rather simple technical solution, compared against the great number of unexpected physiological effects, many of which are still under research. The study of decompression and recompression is complex and involves knowledge of physics and physiology. All precautions mentioned in this article, as well as medical contra-indications to diving for adults apply also to children, but must be carefully adapted[14]. The purpose of this article was to describe some basic principles of diving physics. This text does not substitute a diving course. In order to practice this sport safely there is no need to know all the information given here, but it is mandatory to have a thorough practical and theoretical training, given by a certified SCUBA-diving instructor.
ACKNOWLEDGEMENTS
- The author would like to thank Francisco Fernández for useful suggestions, Guillermo Vázquez for technical assistance, and Gabriela Trucco for designing the figures.
References
| [1] | Heinrich Matthys, Medizinische Tauchfibel, Springer-Verlag, Germany, 1983. |
| [2] | Kay Tetzlaff, Einar Thorsen, “Breathing at depth: physiologic and clinical aspects of diving while breathing compressed gas”, Elsevier, Clinics in Chest Medicine, vol.26, no.3, pp.355-380, 2005. |
| [3] | Carl Edmonds, Bart McKenzie, Robert Thomas, John Pennefather, Diving Medicine for Scuba Divers, 5th ed., Carl Edmonds, Australia, 2013. |
| [4] | Claus-Martin Muth, Ulrich Ehrmann, Peter Radermacher, “Physiological and clinical aspects of apnea diving“, Elsevier, Clinics in Chest Medicine, vol.26, no.3, pp.381-394, 2005. |
| [5] | Jack Jackson, Complete Diving Manual, New Holland Publishers Ltd., United Kingdom, 2005. |
| [6] | Albert A. Bühlmann, Tauchmedizin: Barotrauma, Gasembolie, Dekompression, Dekompressionskrankheit, Springer Verlag, Germany, 1992. |
| [7] | Alfred A. Bove, Bove and Davis´ Diving Medicine, 4th ed., W.B. Saunders Co., USA, pp.225-240, 2004. |
| [8] | Suk Ki Hong, Peter B. Bennett, Keizo Shiraki, Yu-Chong Lin, John R. Claybaugh, “Mixed-gas saturation diving”, in Handbook of Physiology, John Wiley & Sons, Inc., USA, suppl.14, pp.1023-1045, 2011. |
| [9] | David H. Elliott, Peter B. Bennett, Physiology and Medicine of Diving and Compressed Air Work, Harcourt Publishers, USA, 1969. |
| [10] | James M. Clark, Christian J. Lambertsen, “Pulmonary oxygen toxicity: a review”, American Society for Pharmacology and Experimental Therapeutics, Pharmacological Reviews, vol.23, no.2, pp.37-133, 1971. |
| [11] | Stephen Thom, James M. Clark, “The toxicity of oxygen, carbon monoxide, and carbon dioxide” in Diving Medicine, W.B. Saunders Co., USA, p.82, 1990. |
| [12] | Richard L. Pyle, “Multiple gas mixture diving, Tri-mix”, in Scientific Diving: a general code of practice, United Nations Educational, Scientific and Cultural Organization (UNESCO), France, pp.77-80, 1996. |
| [13] | Michael B. Strauss, Robert C. Borer, “Diving medicine: contemporary topics and their controversies“, Elsevier, American Journal of Emergency Medicine, vol.19, no.3, pp.232-238, 2001. |
| [14] | Bernd E. Winkler, Claus-Martin Muth, Kay Tetzlaff, “Should children dive with self-contained underwater breathing apparatus (SCUBA)?”, John Wiley & Sons, Inc., Acta Paediatrica, vol.101, no.5, pp.472-478, 2012. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML