1. Background Information

Interaction (t-way) testing is a methodology to generate a test suite for detecting interaction faults. The generation of a t-way test suite is a n NP hard problem (Zamli, et al., 2013). Many t-way strategies have been presented in the scientific literature. Some early algebraic t-way strategies exploit exact mathematical properties of orthogonal arrays (Zamli, et al., 2013). These t-way strategies are often fast and produce optimal solutions, yet they impose restrictions on the supported configurations and interaction strength. Computational t-way strategies remove such restrictions, allowing for the support of arbitrary configurations at the expense of producing non-optimal solution (Zamli, et al., 2013).

Zamli, et al., (2013) Prior works infer that pairwise testing considering 2-route connection of factors can be viable to distinguish most blames in a commonplace programming framework. While this conclusion may be valid for a few frameworks, it can't be summed up to all programming framework shortcomings, particularly when there are huge associations between factors (R. C. Bryce et al, 2010). For instance, the examination by the National Institute of Standards and Technology (NIST) announced that 95% of the genuine blames on the test programming include 4-way cooperation. Indeed, the greater part of the deficiencies is distinguished with 6-way cooperation. When all is said in done, the thought of higher collaboration qualities can be risky. Rahman, et al, (2014) states that whenever the parameter cooperation scope t increases to more than 2, the number of t-way test sets likewise increments exponentially.¹ For case, think about a framework with 10 parameters, where each parameter has 5 esteems. There are 1,125 2-way tuples (or sets), 15,000 3-way tuples, 131,250 4-way tuples, 787,500 5-way tuples, 3,281,250 6-way tuples, 9,375,000 7-way tuples, 17,578,125 8-way tuples, 19,531,250 9-way tuples, and 9,765,625 10-way tuples.

2. Introduction

From this illustrative case, for a substantial framework with numerous parameters, considering a higher-arrange t-way test set can lead toward a combinatorial blast issue Torres-jimenez, et al, 2013). Therefore, this paper likewise investigates the present best in class and examines the similitudes and contrasts among a few variations of IPOG inside the writing. Moreover, several examinations embraced are talked about to exhibit the speedup pick up. At long last, examinations with other existing methodologies, to be specific, TConfig, Jenny, TVG, ITCH, IPOG, IPOG_D, and IPOF are moreover illustrated. For most cases, MC-MIPOG outflanks other existing systems regarding test size and backings a high level of connection (t).² Whatever is left of this paper is sorted out as takes after. Area II presents a best in class survey of the current techniques, area III gives the points of interest of the proposed MIPOG technique furthermore, how it differs from the first IPOG (Lehmann and Wegener, 2000). Segment IV gives a point by point portrayal of MC-MIPOG and talks about its usage. Segment V reports assessment tests. At last, segment VI expresses our decisions and proposals for future works.

3. Related Work

Zamli, et al (2011) analyses that combinatorial testing methodologies can be delegated either computational or logarithmic systems. Generally mathematical approaches figure test sets straightforwardly by a numerical work.³ Arithmetical methodologies are frequently in view of the augmentations of numerical techniques for building orthogonal exhibits (OA). A few varieties of the arithmetical approach additionally abuse recursion to allow the development of bigger test sets from littler ones (Klaib, 2009). Therefore, the calculations associated with logarithmic methodologies are regularly lightweight and not subject to the combinatorial blast issue.

Thus, procedures that depend on logarithmic approach are amazingly quick. Then again, arithmetical approaches frequently force limitations on the framework arrangements to which they can be connected. This essentially confines the relevance of logarithmic methodologies for programming testing (Lei, 2013). Prior works in combinatorial testing distinguish two procedures (Klaib, 2009), to be specific the programmed effective test generator (AETG) and input parameter arrange (IPO). The AETG fabricates a test set one test at once until all the tuples are secure. AETG and its variations are later summed up into a general system to help multi-way connection (t≤ 6). Interestingly, IPO covers one parameter at any given moment. This permits Initial public offering to accomplish a lower request of multifaceted nature than AETG.

Initial public offering is a pairwise system (cooperation quality t = 2) in view of vertical and even augmentation. Firstly, a pair of test set is produced by the IPO system for both starting variables.⁴ At that point, it keeps on stretching out the test set to produce a pairwise test set for the initial three parameters and keeps on doing as such for each extra parameter until the point that every one of the parameters of the framework are secured by means of flat expansion (Younis, 2010). On the off chance that required for connection scope, IPO likewise utilizes vertical expansion with a specific end goal to include new tests after the fulfillment of flat expansion. Afterward, Initial public offering is summed up into IPOG. A few IPOG variations have been proposed to enhance its execution, including IPOG-D, IPOF, and IPOF2. Both IPOG and IPOG-D are techniques which can be determined. Not at all like IPOG, has IPOG-D consolidated the IPOG procedure with a mathematical recursive development called D-development to diminish the quantity of tuples to be secured. Lei and others detailed that when t = 3, IPOG-D is debased to a D-development arithmetical approach. Now, if t > 3, a minor rendition of IPOG covers the revealed tuples that might have been missed amid D-development.⁵ In that capacity, IPOG-D tends to be speedier than IPOG, however with a bigger test set.

4. MIPOG Strategy

In this area, we present the MIPOG technique and exhibit how it can be parallelized into MC-MIPOG. We likewise feature the likenesses and contrasts between MIPOG furthermore, IPOG (Bryce and Colbourn, 2007). Notwithstanding the way that it is an effective technique, we take note of that the age of a test set (ts) can be temperamental in IPOG (see Fig. 1) because of the likelihood of the present experiment changing amid the vertical expansion (particularly for test cases that incorporate "couldn't care less" esteem). This raises the issue of reliance between already produced test cases and the updated one.To address this reliance issue, we have considered variation calculations for both level and vertical expansion to expel conditions (see the MIPOG procedure in Fig. 2).

Figure 1. IPOG Strategy (Wang, 2003)

Figure 2. IMPOG Strategy (Shaiful, 2016)

For level expansion, the MIPOG system after checking all the estimations of the input variables, picks the esteem that holds the most extreme number of mixes for the revealed tuples in the π set. Additionally, MIPOG upgrades the don't mind esteem. Therefore, MIPOG dependably creates a stable experiment which can't be adjusted via hunting down tuples that can be secured by a similar test. This is performed by methods for thorough looking of revealed tuples that can be joined with this experiment amid level expansion (to guarantee that the experiment is surely advanced).

For vertical enhancement, MIPOG modifies the π set in decremented estimate arrange. MIPOG picks the primary tuple lately from the revised π set what's more, consolidates that tuple with other appropriate tuples in the π set. That is, the subsequent experiment must have the most extreme weight of the revealed tuples found through thorough looking of revealed tuples. As a whole, these tuples are evacuated from the π set once consolidated. This procedure keeps rehashing while the π set is filled to guarantee finish connection scope. To delineate the contrasts amongst IPOG and MIPOG level and vertical expansion, we think about a framework with 4 parameters. Figures 3 and 4 demonstrate the way toward producing a 3-way test set utilizing IPOG and MIPOG, individually. Now, a negligible test set is created by MIPOG (3×2×2=12 esteems), while IPOG creates 14 test cases. As appeared in Fig. 3, IPOG settles on the parameter esteem task right on time in level expansion. Aside from guaranteeing most combines are secured now of task, IPOG too guarantees that every parameter esteem is as similarly adjusted as conceivable. Conversely, MIPOG chooses the parameter esteem task late (see Fig. 4), that is, simply after first filtering all the parameter esteems to yield the most ideal arrangement (with greatest weight). In vertical augmentation, IPOG iteratively checks for revealed t-route mixes from the even expansion and includes the blend into another test in the vertical augmentation, frequently utilizing effectively secured t-way mixes. In a comparative way, MIPOG likewise checks for revealed t-route mixes from the flat expansion. Nonetheless, MIPOG advances the expansion of another test in the vertical augmentation by joining the most revealed t-way blends at whatever point conceivable. This is effectively done when they couldn’t care less esteem. This step, while enhancing the test estimate, additionally builds the by and large calculation of MIPOG.

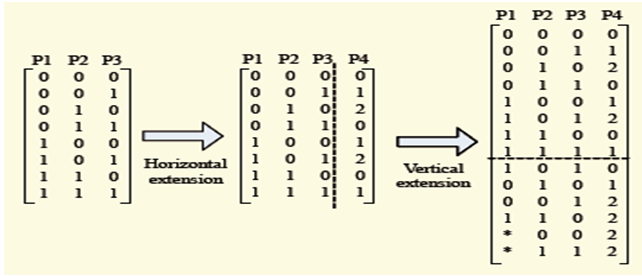Figure 3. Generation of test set using IPOG (Shaiful, 2016)

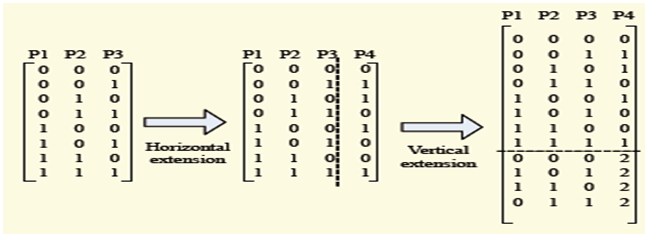Figure 4. Generation of test set using MIPOG (Ramli, 2016)

The net impact of the variation expansion calculations in MIPOG is twofold. To begin with, we can simply get a more ideal test set which would be in any event a similar size or significantly littler than that of IPOG. Besides, there are no conditions between along these lines created test esteems, in this way, allowing the probability of parallelization.⁶ To parallelize MIPOG, we can segment the π set for parameter Pi into vi parcels (see Fig. 2). Therefore, the age of each segment can be performed in a different string. Also, both flat and vertical augmentation can be performed in discrete monitored (synchronized) strings. In the following segment, we talk about the parallel rendition of MIPOG, called MC-MIPOG outlined particularly for Intel Multicore framework.

5. MC-MIPOG Strategy

Worked from MIPOG, the MC-MIPOG system conveys the computational procedures and memory into pieces. In rundown, the MC-MIPOG system execution depends on the following outline criteria: Memory should be conveyed with a specific end goal to hold Pi in moderately autonomous cells, called π[Vi]. Here, each π[Vi] needs its own memory to hold the t-way mixes for a one of a kind specific incentive for the parameter Pi; that is, there are Vi allotments for π. In this case, each segment is produced by a different string, called a combinatorial string. There are Vi isolate strings for even augmentation, called even augmentation strings. Similarly, there are likewise Vi isolate strings for vertical augmentation, called vertical expansion strings. The chose test set is put away into a mutual memory controlled by the test generator (ace) program which controls the creation, synchronization, and cancellation of all of these said strings.

Note that the most recent advancement in multicore frameworks with multitasking working frameworks (as in Linux and Windows) oversees processor/proclivity in an ideal way. This improvement empowers every product string to be mapped into a similar equipment string while at the same time keeping the information near the processor through a procedure called a reserve worm.⁷ Accordingly, the real control of processor and memory partiality is naturally performed by the working framework.

Advantages of An Analogous t-Way Test Generation Strategy for Software Systems MC-MIPOG over other state of arts.

6. Test Generator (Main Program)

As suggested before, the principle program parts are to deal with the shared memory and to arrange strings. Quickly, the principle program fills in as takes after:

Start with a void test set (ts) and produces all tuples for the principal t-parameters.

Create combinational strings (equivalent to the quantity of values in Pi), going to them parameters esteems (P1… Pi-1).

Wait for every combinational string to complete their age, and afterward read π[Vi's].

Shut down the combinational strings.

Create level expansion strings (equivalent to the quantity of values in Pi), going to them π[Vi's], and Vi's for the Pi variable.

For flat augmentation:

For each experiment τ in ts:

Hold up until the point that all strings have approved outcomes.

Read the weight (that is, the quantity of secured tuples in the wake of including the allotted esteem) from each string. At that point, pick the esteem comparing to the greatest weight to be added to ts if no tuples coordinate (weight zero) couldn't care less added to τ.

Tell the flat expansion strings that approve that determination is finished.

As indicated by the choice in c, issue charge to the chosen string to erase tuples from their own π set (πv). Enable the chose strings to refresh τ.

Sit tight for chose string to complete its work.

Shut down the flat strings.

Create vertical augmentation strings equivalent to the quantity of values in Pi, pass them to π[Vi's], and Vi's for the Pi variable.

In vertical augmentation:

Sit tight for the strings to complete their halfway test set (tsvth).

Gather tsvths from the strings. At that point add each tsvth to ts.

Shut down the vertical strings.

For lucidity, the total calculation for the ace program is given in Fig. 5.

Figure 5. Algorithm for master program (Harman, 2014)

Working Threads

In this area, we will portray how each string work.

For combinational strings:

Each string creates its own fractional tuples set (πv).

Each string advises the ace.

For flat expansion strings:

Read next experiment τ in ts.

It is possible in hundred to one that τ does not contain couldn't care less, decide the heaviness of τ.

It is possible in hundred to one that τ contains couldn't care less, the string improves the don't mind an incentive to have however much weight as could reasonably be expected.

Approve the weight by warning.

Sit tight for warning.

Read the summon issued from principle, if it contains erase then the string erases tuples secured by τ from (πv); at that point, attach v to τ (in the event that b) or erase τo (in hundred to one that c) from (πv); then, replace τ with τo.

Because of cancellation in f, advise the holding up process.

For vertical enhancement strings:

Orchestrate πv in diminishing request, pick the principal tuple, also, produce the experiment with most extreme weight.

Rehash step (an) until (πv) is vacant.

Inform the holding up process.

The total calculations for the combinational string, level augmentation string, and vertical expansion string are given in Figs. 6, 7, and 8, individually.

Figure 6. Algorithm for combinational trend

Figure 7. Algorithm for horizontal extension threads (Harman, 2014)

Figure 8. Algorithm for vertical extension thread (Nasser, 2015)

7. Evaluation

Our assessment has three principle points. To start with, we analyze the conduct of MC-MIPOG to that of IPOG as far as the test measure proportion.⁸ Besides, we explore whether there is speedup pick up from parallelizing MIPOG in MC-MIPOG. At long last, we think about the viability of the MC-MIPOG procedure to that of different methodologies (counting that of other IPOG variations) in terms of the produced execution time and test measure.

8. MC-MIPOG Behavior against IPOG

To think about the conduct of MC-MIPOG and IPOG, we played out a gathering of investigations received from Lei and others. In these investigations, we are intrigued to look at the test sizes of MC-MIPOG and IPOG. Note that the IPOG test estimate is gotten from.

Group 1: The quantity of parameters (P) and the qualities (V) are consistent, yet the scope quality (t) is fluctuated from 2 to 7.

Group 2: The scope quality (t) and the qualities (V) are steady to 4 and 5, however the q uantity of parameter (P) is differed from 5 to 15.

Group 3: The quantity of parameter (P) and the scope quality (t) are consistent from t to 10 and 4, individually, yet the values (V) are differed from 2 to 10. The after effects of the tests are appeared in Tables 1, 2, and 3, individually. Here, we characterize the size proportion as the extent of the test set from MC-MIPOG to the size got from IPOG.

Table 1. Size ratio results for 5 to 15 variables with 5 esteems in 4-way testing

Table 2. Size ratio results for 10 variables with 2 to 10 esteems in 4-way testing

Table 3. Size ratio results for 10 variables with 5 esteems for t=2 to 7

From Tables 1 to 3, it is apparent that MC-MIPOG performs superior to anything IPOG as far as test estimate because the size proportion is continuously < 1. In Table 3, NS shows that the parameter and values picked with a given quality are not upheld.

Although contrasting great and IPOG, MIPOG's test estimate isn't the most ideal contrasted with Colbourn's best known distributed outcomes. Regardless, on a positive note, MIPOG adds to finding the ideal test estimate for (t = 5, p = 10, v = 5) that yields 8,169 rather than 8,555 as announced by Colbourn. Indeed, MIPOG likewise reports another ideal test estimate for (t = 7, p = 10, v = 5) that yields 186,664. Note that this result for (t = 7, p = 10, v = 5) has not been accounted for by Colbourn (K. Rabbi, Mamun and Islam, 2015).

9. Speedup Gain in MC-MIPOG

To quantify the speedup, pick up from parallelizing MIPOG, we subjected both MIPOG and MC-MIPOG to three test bunches depicted before. The consequences of the examinations are appeared in Tables 4, 5, and 6. Here, the speedup is characterized as the proportion of the time taken by the successive MIPOG calculation to the time taken by MC-MIPOG calculation.⁹ Every one of the outcomes were acquired utilizing the Linux Centos OS with a 2.4 GHz Core 2 Quad CPU and 2 GB RAM with JDK 1.5 introduced. Note that the execution time is in seconds, and both MIPOG and MC-MIPOG create a similar test set in all cases (Ahmed, et al., 2015).

Table 4. Speedup results for 5 to 15 variables with 5 esteems in 4-way testing

Table 5. Speedup results for 10 variables with 2 to 10 esteems in 4-way testing

Table 6. Speedup results for 10 variables with 5 esteems for t=2 to 7

As found in Table 4, the speedup increments directly as the number of parameters increments. Here, additional overhead is included for the fifth parameters because of the need to begin and close the comparing strings. As found in Table 5, the speedup picks up likewise increments quadratically as the quantity of qualities increments. Extrapolating and performing bend fitting of the outcomes from Table 6, we watch that the speedup increments logarithmically as the quality of scope increments. For this situation, there is too no speedup pick up for this procedure when t = 2, perhaps due to the overhead required for creation, synchronization, and cancellation of strings for a little level of collaboration.

10. Comparison with other Strategies

To explore the viability of the MC-MIPOG procedure against different procedures, including IPOG and its variations, regarding test estimate and the quantity of created test sets, we receive a typical setup framework, the TCAS module. The TCAS module is an air ship impact shirking framework created by the Federal Aviation Administration which has been utilized as contextual analysis in other related works.¹⁰ The TCAS factor contains twelve variables; seven variablescontain 2 esteems, two variables contain three esteems, one variablecontains four esteems, and two variablescontain 10 esteems. As featured before, we picked the TCAS module claiming similar parameters and qualities have been utilized by other specialists. By embracing similar parameters and qualities, target examination might be made between different procedure usage. To guarantee that the outcomes got are up-todate given the way that a portion of the usage have developed enormously finished the years, we downloaded all the accessible usage inside our condition to guarantee reasonable examination. Here, we are likewise intrigued to research regardless of whether every procedure bolsters high (t > 6).

We downloaded ACTS (actualizing IPOG, IPOG-D, IPOF1, and IPOF2) from NIST, ITCH, Jenny, TConfig, and TVGII. We were not ready to download AETG since the execution is a business item; in this manner it was not considered for correlation in our investigation. To repay the way that that Jenny is a MSDOS-based executable program, we picked a running situation comprising of Windows XP 2.0 GHz, an Intel Core 2 Duo CPU, furthermore, 1 GB RAM with JDK 1.6 introduced. Tables 7 and 8 abridge the entire outcomes. As in Table 3 NS demonstrates that the parameter and qualities picked with guaranteed quality are not bolstered. Additionally, obscured cell columns demonstrate the best execution in term of test estimate.

As found in Table 7, MC-MIPOG, IPOG, IPOF1, and IPOF2 gave the ideal test measure at t = 2. At t = 3, both MC-MIPOG what's more, IPOG gave the ideal test measure. For every single other case, MCMIPOG continuously beats different systems. Other than MCMIPOG, only Jenny can bolster more than t = 6 for the TCAS module. Notwithstanding, we have not been effective in summoning Jenny for t > 8 because the program usage crashes.

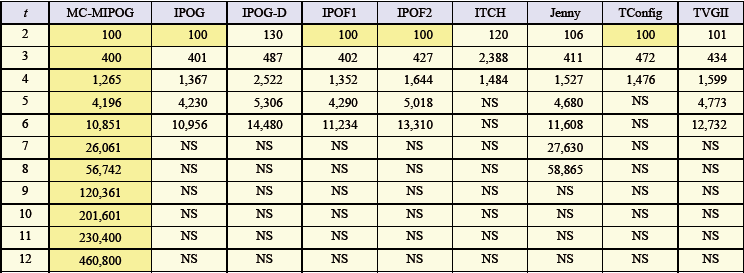Table 7. Comparative test size results using the TCAS module for t = 2 to 12

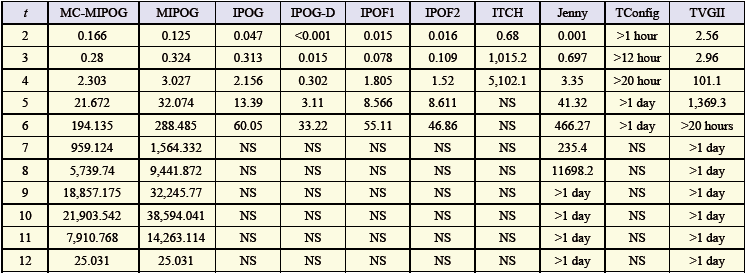Table 8. Comparative test generation time using the TCAS module for t = 2 to 12

Even though TVG empowers the client to choose t from a range from 2 to 9, we can't get any outcome for t = 5 because the program execution crashes. Note that our try different things with TVGII created unexpected outcomes in comparison to the distributed outcomes (here, we utilized the device with the "T_ Reduced" choice), maybe because of another refresh of the execution¹¹. Enabling the client to choose t about 2 and 6, our experience shows that for the TCAS module, TConfig simply gives a result for t < 5. Here, a special case happens when we endeavor to get an outcome for t > 5. A comparative perception can be seen for Tingle. Note that ITCH does not bolster t > 4. Likewise, for the situation of ITCH, the test measure for t = 3 is more prominent than that for t = 4.

11. Conclusions

As PC makers make multicore CPUs unavoidably accessible inside sensible costs, outfitting this innovation is never again an extravagance yet a feasible and helpful choice. In this paper, we explored and assessed a parallel technique called MC-MIPOG for t-way test information age on multicore engineering. Our outcomes demonstrate that MC-MIPOG scales well against existing systems. In arrangement for our future work, we are at present porting MIPOG and MC-MIPOG into the matrix condition. Our underlying usage comes about have been empowering. We are additionally intending to perform more broad correlations with Colburn's best-known outcomes. In examination with all other IPOG variations (aside from MCMIPOG), obviously IPOG beat IPOG_D, IPOF1, what's more, IPOF2 regarding test measure for the TCAS module. Like different systems (aside from MC-MIPOG), this group of procedures can't deliver a test suite for t > 6. That is, no choice is given for t > 6. As far as execution time, IPOG-D has the quickest general time for t ≤ 6. For t > 6, MC-MIPOG is quickest since no different systems can give t-way test age bolster (Jenny underpins up to t = 8). From one viewpoint, MIPOG is like IPOG and IPOG_D in the sense that they are overall deterministic procedures. From another point of view, IPOF and IPOF2, are non-deterministic systems. The general point of IPOG_D, IPOF, and IPOF2 is to accomplish a speedier execution time than that of IPOG. By and large, getting an advanced test measure and a quick execution time are two sides of the same coin¹². Acquiring an improved test measure requires more preparing time for picking the most upgraded tuple. On the other hand, acquiring quick execution time implies that little improvement is performed to get the ideal test measure. This is apparent to the extent the test sizes are worried for IPOG_D, IPOF, also, IPOF2. MIPOG is a procedure that is intended to deliver a littler test estimate than that of IPOG under the cost of something beyond handling time amid flat augmentation. As talked about before, not at all like IPOG, IPOG_D, and IPOF, MIPOG embraces an alternate sort of vertical expansion which is more heavyweight than that of IPOG (for improvement of vertical expansion). Therefore, MIPOG's execution time proves to be slower as compared to the clear majority of the IPOG variations. In any case, the usage of MCMIPOG has lightened this disadvantage through the reception of a multicore design. Truth be told, MIPOG is the main methodology inside the IPOG family that can be parallelized.

Notes

1. Zamli, K.Z., Younis, M.I., Abdullah, S.A.C., Soh, Z.H.C.: Software Testing, 1st edn. Open University, Malaysia KL (2013).

2. R. C. Bryce, Y. Lei, D. R. Kuhn, and R. N. Kacker, “Combinatorial Testing,” Handb. Res. Softw. Eng. Product. Technol. Implic. Glob., 196–208 (2010).

3. M. Rahman, R. R. Othman, R. B. Ahmad, and M. Rahman, “Event Driven Input Sequence Tway Test Strategy Using Simulated Annealing,” in Fifth Int. Conf. on Intelligent Systems, Modelling and Simulation, 663–667 (2014).

4. Lehmann, E., Wegener, J.: Test Case Design By Means Of The CTE-XL. In: Proceedings of the 8th European International Conference on Software Testing, Analysis & Review (EuroSTAR 2000), Copenhagen, Denmark (2000).

5. Lei, Y., Kacker, R., Kuhn, R., Okun, V., Lawrence, J.: IPOG/IPOG-D: Efficient Test Generation For Multi-way Combinatorial Testing. Journal of Software Testing, Verification and Reliability 18(3), 125–148 (2013).

6. K. Z. Zamli, B. Y. Alkazemi, and G. Kendall, “A Tabu Search hyper-heuristic strategy for t-way test suite generation,” Appl. Soft Comput. J.,44, 57–74 (2016).

7. Wang, Z., Xu, B., Nie, C.: Greedy Heuristic Algorithms To Generate Variable Strength Combinatorial Test Suite. In: Proceedings of the 8th International Conference on Quality Software, Oxford, UK, pp. 155–160 (2013).

8. Czerwonka, J.: Pairwise Testing In Real World. In: Proceedings of 24th Pacific Northwest Software Quality Conference, Portland, Oregon, USA, pp. 419–430 (2006).

9. L. Y. Xiang, A. A. Alsewari, and K. Z. Zamli, “Pairwise Test Suite Generator Tool Based On Harmony Search Algorithm (HS-PTSGT),” NNGT Int. J. Artif. Intell.,2, 62–65 (2015).

10. R. R. Othman, N. Khamis, and K. Z. Zamli, “Variable Strength t-way Test Suite Generator with Constraints Support,” Malaysian J. Comput. Sci., 27, 3, 204–217 (2014).

11. Zamli, K.Z., Klaib, M.F.J., Younis, M.I., Isa, N.A.M., Abdullah, R.: Design And Implementation Of A T-Way Test Data Generation Strategy With Automated Execution Tool Support. Information Sciences 181(9), 1741–1758 (2011).

12. A. B. Nasser, Y. A. Sariera, A. A. Alsewari, and K. Z. Zamli, “Assessing Optimization Based Strategies for t-way Test Suite Generation: The Case for Flower-based Strategy,” in IEEE Int. Conf. on Control System, Computing and Eng, 150–155 (2015).