1. Introduction

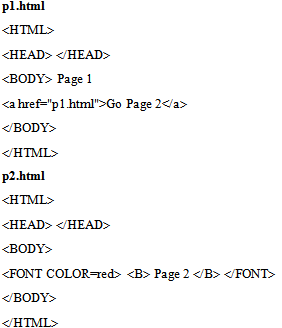
This paper presents a notion introduced by the authors in [8] and [15] together with a new application. The web sites used in this paper consist of web pages which contain only HTML tags.

We will define the verification cost associated to a tag with attributes, respectively associated to a web page and to a web site. A detailed example is presented in section 2, in order to understand the definition of the relation R_TG and the method used to calculate the verification costs. Then, we will define the notion of sink web page, notion used as well in [8], [12] and [15] for different applications.

The relation used in section 2 is used through different methods in [6], [9], [11] and [13] and is dependent on a set of tags TG, chosen based on the web site, in order to have a larger or a smaller number of sink web pages.

In section 3, a method of selecting some web pages is being presented so that by verifying those web pages, others are being implicitly verified. Taking into consideration that a web site can contain a large number of web pages and that the process of verifying them is complex and expensive from the point of view of time, two aspects have been considered: maximizing the number of web pages which are being implicitly verified by the selected web pages and the cost of verifying those selected web pages that should not be higher than a fixed threshold. A web page p is implicitly verified by a web page q if all the tags in p, which are not members of a fixed set TG, can be found in q in the same order.

The algorithm presented in section 3 determines the sink web pages necessary for verification, with the mentioned restrictions.

The effective verification of the web pages is not the target of this paper, taking into consideration the fact that several descriptions of this process have been presented in [2], [3], [4] and [8].

The novelty of this paper consists in the method of defining the cost for verifying a web site and selecting the sink web pages which are necessary in this process.

2. Sink Web Pages

Next, we will consider a web site with the set of web pages

P={p₁, p₂, ... , p_n} and a set TG of tags.

In [12] is defined a relation between two web pages, allowing us to say about a web page if its content can be found in the structure of another web page. Using this relation, we can select from a set P of web pages, some of them that contain all the building tags of the web site. Those web pages are called sink web pages ([8], [12], [15]). Next, we briefly introduce these notions with an example that will be useful in section 3.

For any web page p_i from P, we write T_i the sequence of tags, without their arguments, from p_i, which are not members of TG.

Definition 1

Let TG be a set of tags, p_i and p_j two web pages from P.

We say that T_i=(T_i1, T_i2, ..., T_ia) is in relation ≤_TG with T_j=(T_j1, T_j2, ..., T_jb) and we write T_i ≤_TG T_j, if a ≤ b and there is an index set w={w[1], w[2], ..., w[a]}, with:

1 ≤ w[1] < w[2] < ... < w[a] ≤ b;

T_jw[1] = T_i1, T_jw[2] = T_i2, ..., T_jw[a] = T_ia.

Definition 2

Let TG be a set of tags, p_i and p_j two web pages from P. We say that p_i is in relation R_TG with p_j and we write p_i R_TG p_j, if:

i) T_i ≤_TG T_j;

ii) For any tag from T_j which appears in T_i as well, if it has a closing tag <\Tg> in T_j, then <\Tg> is also in T_i.

Example 1

Let us consider a web site with seven web pages:

P = {p₁, p₂, p₃, p₄, p₅, p₆, p₇}. p_i can be found in the file pi.html, where i{1, 2, ... , 7}.

According to previous definitions, we obtain the following pairs of pages which are in relation R_TG one with each other:

p₁ R_TG p₇;

p₂ R_TG p₃; p₂ R_TG p₄ ;

p₅ R_TG p₄; p₅ R_TG p₆ ;

p₆ R_TG p₄.

Definition 3

The web page p_i is called sink web page, if the following property is fulfilled:

There does not exist p_j in P, with i ≠ j and p_i R_TG pj.

Using the relation R_TG, we can construct for the web site an oriented graph G=(X,U) as below:

X={1, 2, ..., n} is the set of nodes. Each web page p_i from P, where 1 ≤ i ≤ n, has one and only one node in X, associated to it. The relation between a node in X and its corresponding web page from P is the following: the web page p_i has associated the node i.

U = { (i, j) | p_i R_TG p_j, i ≠ j, 1 ≤ i, j ≤ n } is the set of edges.

For any set A we denote by |A| the number of elements of the set A.

Writing d₊(i) = |{(i,j) | (i,j) U}| as being the exterior degree of the graph G, we obtain:

Proposition 1

If i, 1 ≤ i ≤ n is a node in the oriented graph G previously defined, with d₊(i) = 0, then p_i is a sink web page.

The proof is immediate, taking into consideration the definition of the sink web page.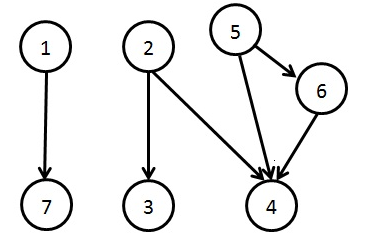

Figure 1. The oriented graph G for a web site with 7 web pages and the relation RTG given by the edges

For the web site with n=7 web pages, from example 1, we obtain the following sink web pages: p₃, p₄, p₇ (Figure 1).

Algorithms of determining the sink web pages from a web site are described in [9] and [11].

3. Defining the Cost of Verifying a Web Page

Similarly to previous sections, we will take a fixed set of tags TG. We will consider p being a web page which contains only HTML tags, with the sequence of tags that are not in TG, T, defined in section 2. For p, we will define the verification cost, C(p), as a function which depends on the cost of verifying the tags.

Let tg be an HTML tag. For tg, we write A_tg as being the set of attributes of tg.

Definition 4

Let the verification cost of tg be c(tg)=1+|A_tg|.

Definition 5

Let the verification cost of a web page p as a function of TG be:

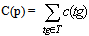Definition 6

Let the verification cost of a web site WA, with the set of web pages P = {p₁, p₂, ..., p_n}, as a function of TG be:

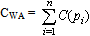For the example 1 from section 2, we have:

C(p₁) = 2+1 = 3;

C(p₂) = 2+1+1+1 = 5;

C(p₃) = 2+1+1+1+1+3+1 = 10;

C(p₄) = 2+1+1+1+4+1+1+1+4 = 16;

C(p₅) = 2;

C(p₆) = 4+1+1+2 = 8;

C(p₇) = 4+1+2+1 = 8;

Considering those costs, we obtain C_WA = 3+5+10+16+2+8+8 = 52.

The cost of verifying a web site can be diminished, if we use for verification only the sink web pages.

Definition 7

Let the cost of implicit verification of the web site WA, with the set of sink web pages S = {s₁, s₂, ..., s_k}, be:

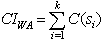For the above previous, we obtain: CI_WA = C(p₃) + C(p₄) + C(p₇) = 10 + 16 + 8 = 34.

Definition 8

Let the cost of implicit verification of the web site WA, with the subset of sink web pages US, where S={s₁, s₂, ..., s_k} is the set of sink web pages, be:

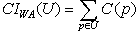Remarks

1. 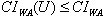, for any ;

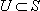2. .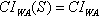

4. Algorithm of Determining the Sink Web Pages for Verifying a Web Site with a Fixed Cost

We will consider a web site with the set web pages P = {p₁, p₂, ..., p_n}, a set of tags TG and a fixed cost k, which is a natural number. Our target is to determine those web pages that maximize the number of implicitly verified web pages with the total cost of verification less than or equal to k.

In order to diminish the total cost of verification, certain web pages will be implicitly verified, through other web pages. A considerable improvement is obtained if we use the sink web pages.

For the example in section 2, if we fix k=25, choosing the web pages 4 and 7, there can be verified directly or implicitly the web pages number 1, 2, 4, 5, 6, 7 with a cost equal to 24 ≤ 25.

The proposed algorithm has the following input data:

- the path of the folder with the web site to be verified

- the path of a text file which contains the TG set

- the fixed maximum cost k

The algorithm will return the following output data:

- the total number of web pages that can be verified within the fixed cost (directly or implicitly)

- the cost of verification

- the web pages that can be directly or implicitly verified with a cost less or equal than k

The algorithm consists of three parts:

- Using the previously defined relation (R_TG), the graph G associated to the web site is determined. It is memorized in an array (a_ij)_1≤i,j≤n, with a_ij=1 if p_i R_TG p_j and a_ij=0 otherwise.

- The array s=(s₁, s₂, ..., s_n) is determined. For each i, 1 ≤ i ≤ n, s_i=0 if p_i is a sink web pages or s_i=j if p_i is not a sink web page and p_j is a sink web page which fulfils the condition p_i R_TG p_j.

- Using dynamic programming (the knapsack problem), some sink web pages are selected so that their verification cost is less than or equal to k and the number of directly and implicitly verified web pages is maximum.

read the input data

read the tags from TG set

read the tags from each web page from the web site// cost[i]= verification cost for web page i, i=1,n

for i=1,n do

cost[i]=0;

while (exist tag Tg in web page i) and (not(Tg in TG)) do

cost[i]=cost[i]+ (1+ number of attributes from tag Tg)

read Tg from web page i

endwhile

endfor

//create the graph

for i=1,n do

for j=1,n do

a[i][j]=0

if i!=j then

if pi is in relation R_TG with pj then

a[i][j]=1

endif

endif

endfor

endfor

//s=(s[1],...,s[n]) with the meaning from the above description

for i=1,n do

s[i]=0

endfor

for i=1,n do

for j=1,n do

if s[j]=0 and a[i][j]=1 then

s[i]=j

endif

endfor

endfor

sw=1

while sw=1 do

sw=0

for i=1,n do

t=s[i]

u=s[t]

v=s[u]

if t!=0 and u!=0 and v=0 then

s[i]=u

sw=1

endif

endfor

endwhile

//p[1]-first sink web page, p[2]-second sink web page, ...

//nrp[i] the number of web pages verified through pi

for i=1,n do

nrp[i]=1

endfor

nrsink=0

for i=1,n do

if s[i]=0 then

nrsink=nrsink+1

p[nrsink]=i

else

nrp[s[i]]=nrp[s[i]]+1

endif

endfor

//dynamic programming method

ct[0]=0

for i=1,k do

ct[i]=-1

endfor

for i=1,k do

for j=1,nrsink do

if cost[p[j]]<=i then

if ct[i-cost[p[j]]]!=-1 and use[i-cost[p[j]]][j]=0 then

if ct[i]then

ct[i]=nrp[p[j]]+ct[i-cost[p[j]]]

for h=1,nrsink do

use[i][h]=use[i-cost[p[j]]][h]

endfor

use[i][j]=1

endif

endif

endif

endfor

endfor

//write data

max=-1

for i=1,k do

if ct[i]>max then

max=ct[i]

j=i

endif

endfor

if max=-1 then

write "no solution"

else

write "number of verified web pages " max

write "cost for verification " j

endif

Implementing this algorithm using Java language has led to the results presented in Table 1. The tests were used for different values of the set TG, as follows:

Table 1. nWS, cWS and k for the journal web site WS TG k=10000; Number of HTML files = 283 Cost of verification (cWS) Number of sink web pages Number of directly verified web pages (nWS) Number of directly and indirectly verified web pages TG0 9976 47 5 201 TG1 9227 46 4 207 TG2 9227 42 4 209 TG3 9365 40 5 222 TG4 9317 40 5 222 TG5 9829 28 7 253 TG6 9799 28 7 253 TG7 9799 28 7 253 TG8 9799 28 7 253 TG9 9799 28 7 253

We wrote nWS the number of web pages, respectively cWS the provided cost which does not exceed k as output data to Java program.

5. Conclusions

The algorithm described in section 3 has provided good results with the tested examples. Next, the authors intend to build a more complex application, which should use the notions and the presented algorithm, and test it on a larger set of web sites. Meanwhile, it is considered that the method of calculating the verification cost for a web page can be improved, by considering the possible values that the tag attributes can have, as well as the method of selecting web pages within the algorithm.