-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Science and Technology
p-ISSN: 2163-2669 e-ISSN: 2163-2677
2018; 8(2): 35-45
doi:10.5923/j.scit.20180802.02

Arc Motion in Low Voltage Circuit Breaker (LVCB) Experimental and Theoretical Approaches
J. Quéméneur, J. Lu, J-J. Gonzalez, P. Freton
Université de Toulouse, UPS, CNRS, INPT, LAPLACE (Laboratoire Plasma et Conversion d’Energie), France
Correspondence to: J-J. Gonzalez, Université de Toulouse, UPS, CNRS, INPT, LAPLACE (Laboratoire Plasma et Conversion d’Energie), France.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This paper is related to the study of the arc motion in simple low voltage circuit breaker geometry. Experimental and theoretical approaches are investigated respectively by fast camera and by a magneto hydrodynamic model. Two theoretical methods have been developed to characterize the arc movement called MECM (Mean Electrical Conductivity Method) and GCRM (Global Current Resolution Method). The results obtained by the two models are in good agreement with the experimental observations. The MECM allows obtaining faster results but the stagnation phases are well represented with the GRCM and this last method is easier to implement in more complex geometry. The results show also the importance of the exhaust description on the arc behavior.
Keywords: Low voltage circuit breaker, Experiments, Plasma modelling, Arc motion
Cite this paper: J. Quéméneur, J. Lu, J-J. Gonzalez, P. Freton, Arc Motion in Low Voltage Circuit Breaker (LVCB) Experimental and Theoretical Approaches, Science and Technology, Vol. 8 No. 2, 2018, pp. 35-45. doi: 10.5923/j.scit.20180802.02.
Article Outline
1. Introduction
- Low voltage circuit breaker (LVCB) is key element of electrical equipment in the power distribution systems. It is used to protect electrical machines from power defaults and to protect humans. In LVCB, when a fault current occurs, the contacts are separated and arc plasma appears between them. During the arc life, the protection is not effective as an arc exists first between one runner and a moving contact then between the two runners. This arc is submitted to electromagnetic and gas flow forces. The electromagnetic forces are due to the current circulation in the runner and in the arc plasma, creating respectively external and auto induced magnetic fields. Under the influence of these forces and due to the bending of the arc, generally the arc jump from the moving contact to the runner before the total opening of the moving contact [1]. Then the arc under the influence of magnetic forces and gas pressure [1, 2] is pushed into the plates to be split, cooled and extinguished by the effect of the current intensity limitation [2]. A general scheme of LVCB is presented Figure 1. During the arc life its motion depends on several effects: (1) LVCB uses the polymers vapors as polyoxy-methylene (POM) or polyamide 6 (PA6) coming from sidewalls. Vapors are ablated from sidewalls due mainly to plasma radiation. They change the plasma properties and increase the arc velocity [3]. We can quote papers from the literature studying the plasma properties of mixtures composed by air and PA6 [4-6]. These data banks are used by authors who have studied the plasma-wall interaction and the influence of the vapors on the arc behavior [7].
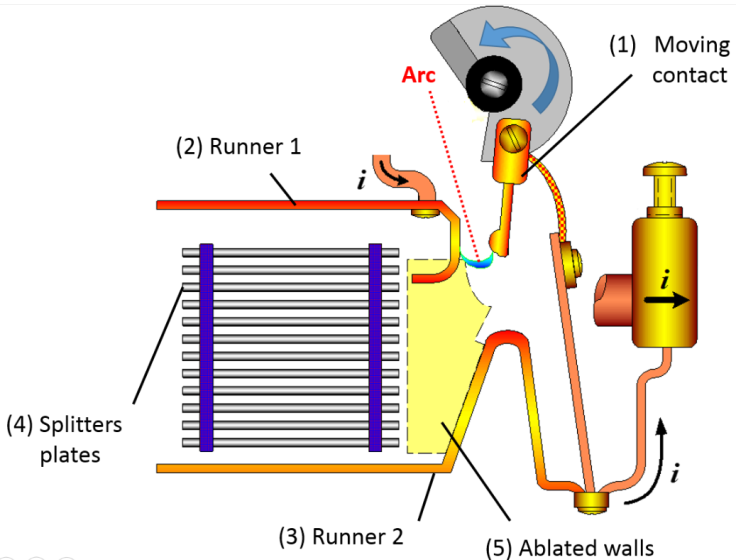 | Figure 1. General scheme of LVCB |
2. Numerical Model
2.1. The Geometry
- Miniature Circuit Breakers (MCBs) are evolved in very complex geometries that lead for their study to meshing difficulty and make the interpretation complicated. Thus we choose to simplify the LVCB arc chamber to a 3D rectangular box with two parallel arc runners leading to a unidirectional arc displacement (Figure 2). Thus geometric parameters can be clearly defined: length, width, height, initial position of the arc, size of the gas exhausts. Moreover, such geometry can be easily meshed with hexahedra cells which provide higher mesh quality than tetrahedral and therefore a faster convergence of the calculation.
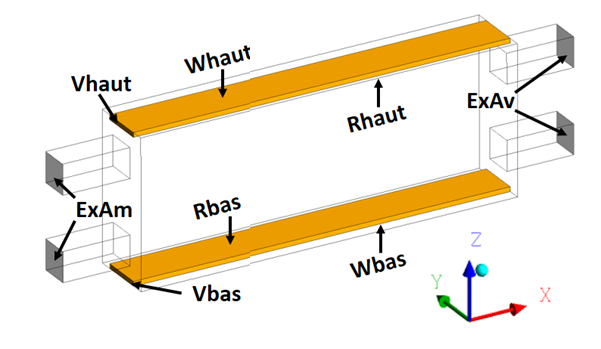 | Figure 2. Simplified arc chamber geometry studied |
2.2. Hypothesis
- To reduce the calculation time and simulation complexity, several assumptions have to be made:1) The medium is in Local Thermodynamic Equilibrium (LTE). This hypothesis has been validated [38] for the arc column but is arguable for peripheral region of the discharge and false in the plasma sheaths [30].2) The special physic of the sheaths is ignored [26];3) Turbulence is not taken into account;4) Ferromagnetic effects or eddy currents are neglected; the induced current is assumed to be small in comparison with the applied current and its influence on the total current distribution is neglected [26, 39, 40]5) The medium is assumed to be pure air as the walls ablation is not taken into account;6) Arc ignition is not modelled. Calculation is started with a conductive channel which is either a fixed temperature if the gap is small or an energy source term applied for a short time in the case of a gap superior to several millimeters [26];7) Gravity is neglected.
2.3. The Equations
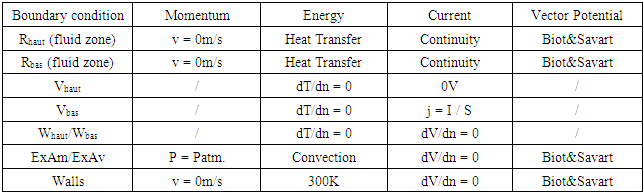
- We use the Patankar formulation (Equation 1) to solve the magneto-hydrodynamics equations in transient state in a 3D coordinate system with a finite volume method (FVM). The diffusion coefficient ΓΦ and the source term SΦ depend on the physical quantity Φ considered as described in Table 1 where P is the pressure; Bx, By and Bz are the components of the magnetic field on the x,y,z directions; Jx, Jy and Jz are the components of the current density on the x,y,z directions; εn is the net emission coefficient, kb is the Boltzmann constant, e is the elementary charge and µ0 is the void magnetic permeability.
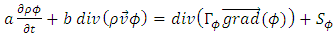 | (1) |
|
2.4. Methods for Arc Motion
- Whereas the electrical arc model described above is commonly accepted and used [43], there is no consensus on the way to describe arc-wall interaction and arc root movement on the electrodes. Nevertheless, this arc displacement is a critical point of the LVCB operation. For this purpose, one can describe an energy exchange at the plasma/material interface or adapt electrical conductivity in this region.Early works on arc movement modelling have been performed in the Technical University of Braunschweig in 1998 [44]. Arc attachment uses the Richardson’s law which describes the thermo-ionic emission on a hot cathode, but the electrode material considered is copper which boiling point is under 3000K. Not taking into account emission by field effect could leads to errors on current density calculation up to 175% [45]. Another arc displacement method [33, 31] developed by the same group is more widely used [19, 18]. This is an empirical sheath model where the electrical conductivity in the cells adjacent to the electrode is not calculated with the gas properties but determined by the current density. Based on sheaths voltage drop measurements, a non-linear conductivity is fixed to obtain 10V on the layer surrounding the electrode. This has the two advantages of achieving a correct estimation of the total arc voltage and ensuring a sufficient electrical conductivity close to the electrode to allow a small current to flow. In the work of Piqueras et al. [46], arc attachment is self-determined with very few adjustment parameters. The voltage difference between anode and cathode is controlled so that the current gets the required value. Furthermore, electrical conductivity in the cell neighboring the electrode is imposed as the one of the metal to make sure the current can easily flow out of the electrode.In the method developed by Rondot [47], an energy balance on the plasma/material interaction is tuned with adjustment parameters. Like in the work of Piqueras [46], there is a layer of 1 mm with high electrical conductivity all around the electrodes.A more precise description of the physic of the anode [48] and cathode [30] would be a solution to simulate the arc movement but may be too complicated to implement and may cost a precious simulation time. In this work, we used two different arc movement methods to compare and confront the results to the experiments.
2.4.1. Mean Electrical Conductivity Method (MECM)
- This first method is an improvement of Swierczynski's work [3]. The calculation domain close to the electrodes is separated in slices along the axis of displacement. The arc position is set where the mean electrical conductivity at the vicinity of the electrodes is maximal. The mean electrical conductivity is calculated in each slice and the position of the arc root is set at the coordinate with the highest mean value. The electrical conductivity of the cell is calculated depending on the local pressure and temperature. As seen in experimental works [49, 50], there is more than one current path during arc commutation and restrikes. Thus, to model those processes, it is necessary to allow at least two arc roots on each runner. Therefore, the algorithm searches for slices where electrical conductivity is a local maximum. The two coordinates with the highest values being the positions of two arc roots. The total current is then shared between the two paths proportionally to the conductivity level (Figure 3). These positions are searched for each time step and classical steady state boundary conditions for anode and cathode may be used. For the anode position given by the algorithm, the scalar potential is imposed to zero volts and the electrode temperature is allowed to rise with a null Neumann condition. For the cathode, the current is imposed in the simulation with a parabolic current density distribution like in the work of Hsu [38] or Freton [51]. However due to a small width of the electrode and as the current can rise up to several kA the arc attachment can adopt an elliptic shape to allow more current to flow. Figure 4 shows the parabolic current density profile and the elliptic arc root shape that are determined by Equations 2-4.
 | Figure 3. Example of arc root determination on one electrode |
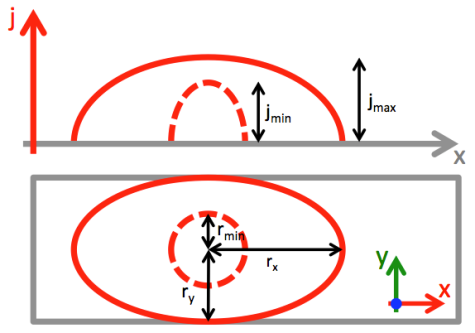 | Figure 4. Rendering of the current density profile on the electrode |
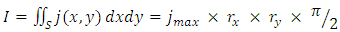 | (2) |
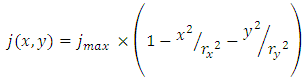 | (3) |
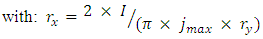 | (4) |
2.4.2. Global Current Resolution Method (GCRM)
- Another method considers heat and current exchanges between the electrodes and the plasma. The difficulty of this method is that the thermal and electrical conductivities between metal and plasma medium are very different. Therefore, improved algebraic multigrid methods [52] must be used to ensure current conservation. These results are obtained with a longer calculation time than the MECM.The current is imposed in the simulation in the left end of the rail Vbas (Figure 2). The number of arc roots per electrode is undetermined, and varies from one to several. This method allows describing arc commutation and restrikes [53] and a self-determination of the arc movement without any adjustment parameters. Another advantage is its adaptability to complex geometries.
2.5. Boundary Conditions
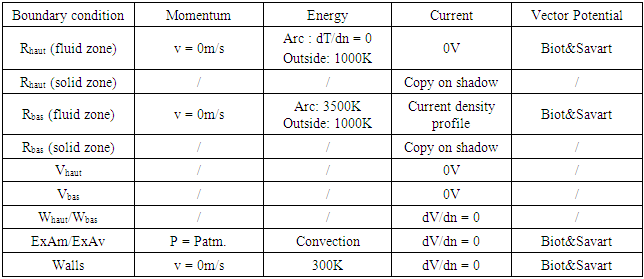
- The geometry for the simulation is given in Figure 2 with the two rails (Rbas and Rhaut) and two gas exhausts on each side of the chamber (ExAm and ExAv). Current is fed through Vhaut and leaves the calculation domain through boundary Vbas thus the lower rail is the cathode. Whaut and Wbas are the back side of the rails and aren’t crossed by any flux. The other boundary conditions are labelled “Walls” in Tables 2-3 and refer to the plastic walls of the chamber.
|
|
3. Experimental Study
3.1. Arc Chamber
- Due to the lack of space, natural MCB chambers are curved which makes analysis of the movement more complicated. To realize a parametric study we need to define simple arc chamber geometry. Thus, we use the same rectangular geometry for both the experiment (see Figure 5) and the 3-D model. The walls are in PMMA, the front side being a transparent Plexiglas to permit optical measurements. The arc chamber has two parallel steel arc runners and two exhausts (2x19.6mm2) on each lateral side. The electrical arc is ignited by a fuse wire.
 | Figure 5. Rectangular geometry for experimental and model studies |
3.2. Pulse Current Source
- In our study, we focus on short-circuit fault in MCB that can reach prospective values up to 20kA. We therefore need an electrical source able to reproduce such current pulse. Four LC resonant circuits tuned to 50Hz are used in order to obtain a prospective peak current up to 13kA. The choice of the inductor-capacitor pair and the charging voltage allows adapting the current value according to equation 5.
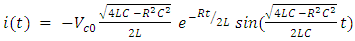 | (5) |
3.3. Instrumentation
- For high-speed imaging of the arc, we use a Photron Fastcam SA5, which can reach 1Mframe/sec. In ours measurements we use 100kframe/sec in order to keep a good resolution. The size of arc chamber being in the same order as the size of the CCD matrix we use a macro lens with a 105mm focal length. As the electrical arc is too bright, the aperture is kept minimal, which also improves the depth of field. Moreover, a neutral density filter of 128 is added and exposure time can be reduced to avoid overexposure of the picture and therefore loss of information. “Classical” electrical measurements are also performed with a differential voltage probe and Rogowski coils for the measurement of the current intensity.
3.4. Post-Treatment Software
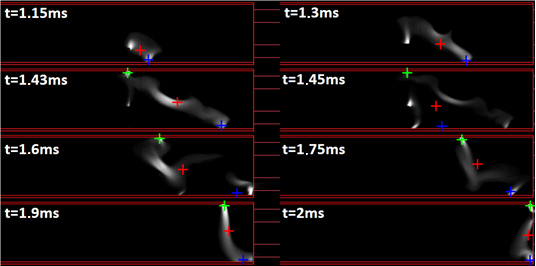
- Breaking arcs present chaotic behaviors so it is better to perform statistical analysis on the experimental results before any interpretation. There are also some phenomena that are difficult to quantify such as restrikes, commutation and arc movement and an arbitrary determination by the user could lead to biases and randomness. For that matter, one tool was developed and used for the analysis. The plasma in presence of an arc discharge is a bright and diffuse medium. To determine its position and movement from the pictures of the high-speed camera, a method must be specified. As suggested by McBride & al. [54], the arc can be tracked with a weighted average of the light intensity. In our study, the Centre Of Intensity (COI) method is used on all pixels of the frame or on specified areas like the vicinities of the runners in order to determine the global position of the arc or the positions of arc roots on the electrodes. For a direct confrontation between experimental results and simulation, the same software is used to analyze the theoretical and experimental results. In this case the theoretical radiative losses obtained by the model need to be displayed in grayscale. The results of the model then are treated like experimental ones using the same algorithm for greater relevance. Typical pictures from the high-speed camera are displayed in Figure 6 and the adapted views of net emission coefficient are shown in Figure 7, we can observe similitude on the arc behavior between the theoretical and experimental results.
4. Comparison of the Arc Motion Model
- The methods to describe the arc moving on the electrodes must be validated. Therefore, in the same geometry, an arc is initiated between the two rails with a fuse wire in the experiment and by a conductive channel at the same position in the simulation. The displacement is characterized in Figures 8-9, I=1560A and the gas exhausts of the chamber are close or open.
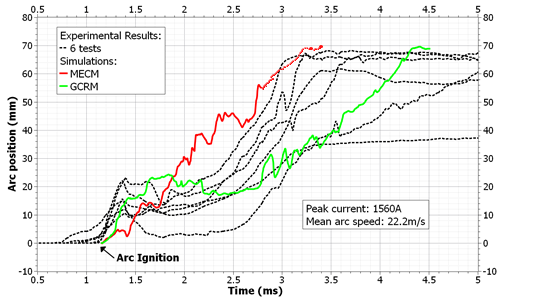 | Figure 8. Experimental and simulated arc movements for fully open gas exhausts at medium current Peak current value 1560A |
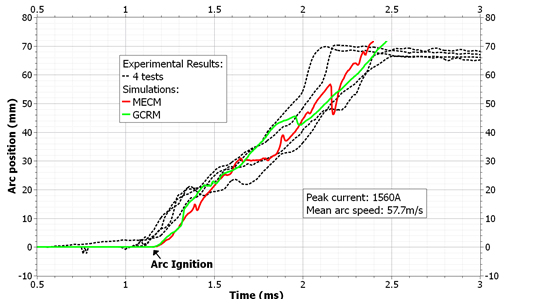 | Figure 9. Experimental and simulated arc movements at medium current with closed upstream exhausts Peak current value 1560A |
5. Conclusions
- This work was related to the study of the arc motion in low voltage circuit breaker configuration. Due to the phenomena complexity and in order to well separate the motion phase, a simple geometry is chosen allowing the arc characterization by experiments and theoretical ways. A half wave current (10ms) for several current intensity values and different configurations (exhausts opened or closed in upstream and downstream positions) were used. A synchronized system is used to switch on the frames acquisition and the electrical measurements (current and voltage). Fast camera allows observing the arc movement along the runners and a special tool was developed for an automatic treatment of the videos. Several current intensities and different exhaust configurations have been tested. Due to experimental results disparities the measurements were realized several times for the same conditions.Using the same geometry, one transient 3D magneto hydrodynamic model based on the commercial fluent software was built, allowing characterizing the plasma with the electric arc. The arc movement is driven by pressure and electromagnetic forces. Specific attention was given to the calculation of the magnetic field. It is calculated by the vector potentials resolution however the boundary conditions are determined by the Biot & Savart formulation. To describe the arc movement, two methods are implemented and tested the MECM and the GCRM. Each methods has its advantage and inconvenient. The MECM necessitates the resolution of two more equations for the resolution of the current conservation in the two runners. The arc attachment position is self-determined and specific condition is assumed with a current density distribution on a given area. The vicinity of the runners is split in interval allowing determining the mean electrical conductivity. The length of this layer is one parameter which can be adjusted if necessary. Searching the maxima of the mean electrical conductivity allows determining one or more arc root positions.The GRCM is simpler as only one equation is solved to assume the current conservation. Nevertheless due to several order differences between the electrical conductivity of the plasma and the material specific cycles need to be made to conserve the current. No limitation on the number of arc root exists.The radiation term (net emission coefficient) allows analyzing the results using the experimental tool developed. The two arc motion methods give similar results and are in good agreement with the experimental results. They allow describing stagnations and restrikes phases. Nevertheless even if the MEC Method is faster, the GRC Method is easier to implement in more complex geometry as we don’t have to define and control the vicinities of the runners.
ACKNOWLEDGEMENTS
- We acknowledge financial support from HAGER Company. We are also grateful to P. Joyeux and G. Deplaude for their help and fructuous discussions.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML