Abdulsalam Ya’u Gital1, Muhammed Abdulhameed2, Bala Ma’aji Abdulhamid1, Muhammad Sirajo Aliyu3, Aliyu Danladi Hina4
1Deaprtment of Mathematical Sciences, Faculty of Science, Abubakar Tafawa University Bauchi, Nigeria
2Department of Mathematics Faculty of Science, Universiti Tun Hussein Onn, Malaysia
3Department of Science, Collage of Science and Technology, Hassan Usman Katsina Polytechnic, Katsina Nigeria
4Department of Basic Studies, The Federal Polytechnic Bauchi Nigeria
Correspondence to: Abdulsalam Ya’u Gital, Deaprtment of Mathematical Sciences, Faculty of Science, Abubakar Tafawa University Bauchi, Nigeria.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, an attempt has been made for the analytical solution of the unsteady mixed convection flow induced by the combined effects of the mechanically driven lid and the buoyancy force within rectangular enclosures. The couple of nonlinear equations describing the fluid behavior and temperature distribution within rectangular enclosures form a very complex system where the analytical solution is not available in the literature. To the best of the author's knowledge, this the first time such an attempt is presented. To drive the solutions of the coupled nonlinear boundary systems, an optimal homotopy asymptotic method was applied in the initial stage, then follow by the method of eigenfunction combined with orthogonality property. Explicit analytical solutions for both fluid velocity and temperature distribution are obtained. The results proved the effective technique for solving the couple nonlinear equations in a rectangular enclosure.
Keywords:
Optimal homotopy asymptotic technique, Mixed convection, Heat transfer, Stream function, Isotherms
Cite this paper: Abdulsalam Ya’u Gital, Muhammed Abdulhameed, Bala Ma’aji Abdulhamid, Muhammad Sirajo Aliyu, Aliyu Danladi Hina, Free Convection Flow in Rectangular Enclosures Driven by a Continuously Moving Horizontal Plate, Science and Technology, Vol. 5 No. 3, 2015, pp. 45-56. doi: 10.5923/j.scit.20150503.02.
1. Introduction
Considerable attention has been paid in recent years to the problems heat transfer analysis rectangular domain with regular boundary conditions yielding a well-posed problem. The governing couple equations are very complicated and highly nonlinear, with mostly numerical solutions. The theoretical studies of mixed convective flow in a lid-driven cavity finds applications in flow and heat transfer in solar ponds and solar collectors, dynamics of lakes, reservoirs and cooling ponds, cooling of electronic systems, thermal-hydraulics of nuclear reactors, thermal convection in micropolar fluids, chemical processing equipment, lubricating grooves, crystal growing, materials processing such as float glass production, galvanizing, metal coating and casting, food processing, and industrial processes where a solid ribbon or a solid material is heated as it moves through a furnace, among others [1-10].The above literature shows that the convective heat transfer and flow in a rectangular enclosure driven by a horizontal wall while being cooled from one horizontal and vertical wall, with the other vertical wall thermally isolated have not been investigated. This configuration finds practical applications in the cooling of an extruded plate in a hot rolling process. The fluid flow and the heat transfer patterns within the enclosure dictate the degree of cooling and hence the quality of the final product. This fact motivates the present study. The purpose of this work is therefore to present a parametric investigation of the Richardson and Prandtl numbers, and the aspect ratio on the flow patterns, energy distribution and heat transfer behaviour for this configuration.The aim of the present work is to solve the problem of mixed convection flow in rectangular enclosures driven by a continuously moving horizontal plate using an analytical technique, OHAM. In view of this we have established an analytic solution based on the OHAM to venture further into the regime of nonlinear fluids.
2. Analytical approach
We start with the basic idea of OHAM, the governing equations to solved are classified into two velocity 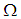 and temperature
and temperature 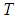 that is
that is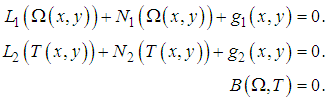 | (1) |
where  are linear operators,
are linear operators, 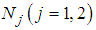 are non-linear operators,
are non-linear operators, 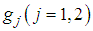 are known function and
are known function and  is a boundary operator.Construct an optimal homotopy
is a boundary operator.Construct an optimal homotopy 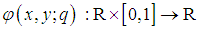 which satisfies the following equations:
which satisfies the following equations: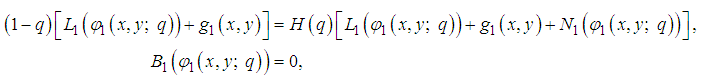 | (2) |
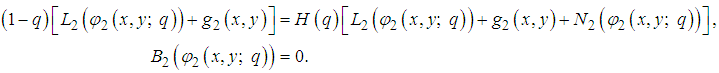 | (3) |
where  and
and  is an embedding parameter,
is an embedding parameter, 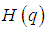 is a nonzero auxiliary function for
is a nonzero auxiliary function for 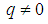 and
and 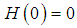 , and
, and 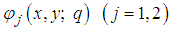 are unknown functionsClearly, when
are unknown functionsClearly, when 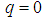 and
and 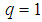 it holds that
it holds that 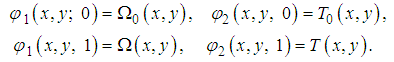 | (4) |
Choose the auxiliary function 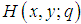 in the form
in the form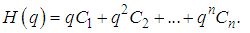 | (5) |
where 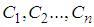 are constants to be determined.Construct a Taylor's series solution of equations (2) and (3) in the form
are constants to be determined.Construct a Taylor's series solution of equations (2) and (3) in the form 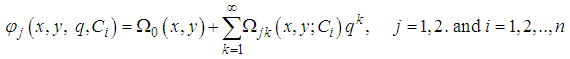 | (6) |
substituting equation (6) into equations (2) and (3) and boundary and equating the coefficients of like powers of 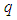 to obtain
to obtain 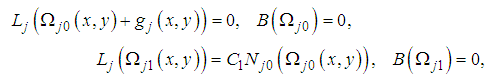 | (7) |
and the 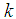 th order equation is defined by
th order equation is defined by 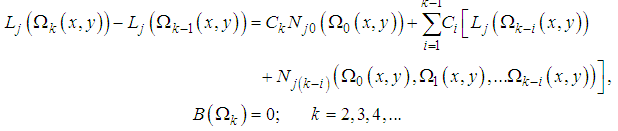 | (8) |
where 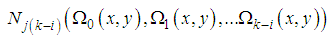 is the coefficient of
is the coefficient of 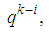 obtained by expanding
obtained by expanding 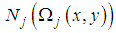 in series with respect to the embedding parameter
in series with respect to the embedding parameter 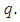
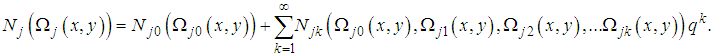 | (9) |
The solution of equation (1) can be approximately obtained in the form 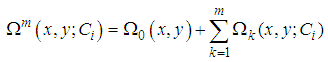 | (10) |
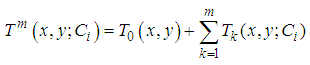 | (11) |
Substitute equations (10) and (11) into equation (1) it results the following expression for residual: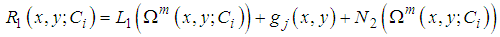 | (12) |
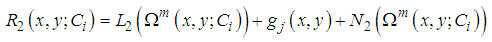 | (13) |
If 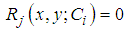 , then (10) and (11) will be the exact solution. Generally such a case will not happen for nonlinear problems, but we can minimize the functional by the method of lease squares
, then (10) and (11) will be the exact solution. Generally such a case will not happen for nonlinear problems, but we can minimize the functional by the method of lease squares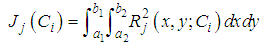 | (14) |
where 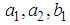 and
and 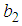 belong to the domain of the problem. Finally, the unknown constants
belong to the domain of the problem. Finally, the unknown constants 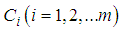 can be optimally identified from the conditions
can be optimally identified from the conditions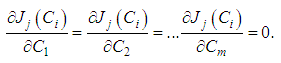 | (15) |
With these known values of 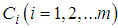 , the approximate solution of equation (10) and (11) are well determined.Statement of the problemIn the present investigation, we consider convective heat transfer and flow in a rectangular enclosure driven by a horizontal wall, the horizontal plate divides the rectangular enclosure into equal halves while being cooled from one horizontal and vertical wall, with the other vertical wall thermally isolated as described by Waheed [1] Figure 1 show the physical configuration.
, the approximate solution of equation (10) and (11) are well determined.Statement of the problemIn the present investigation, we consider convective heat transfer and flow in a rectangular enclosure driven by a horizontal wall, the horizontal plate divides the rectangular enclosure into equal halves while being cooled from one horizontal and vertical wall, with the other vertical wall thermally isolated as described by Waheed [1] Figure 1 show the physical configuration.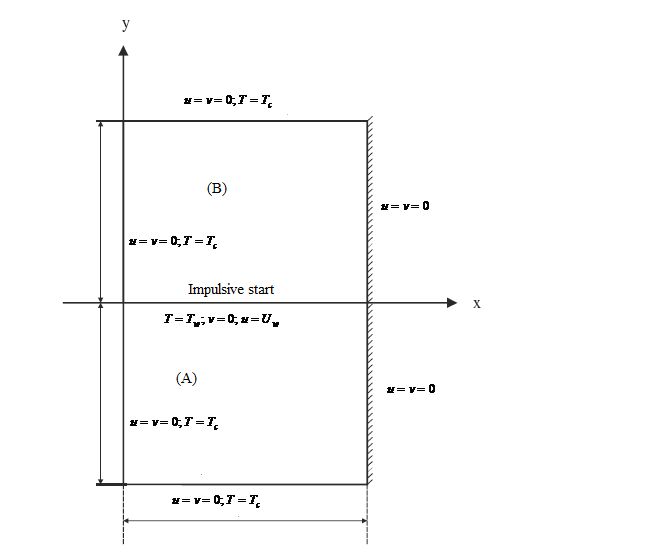 | Figure 1. Physical configuration |
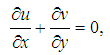 | (16) |
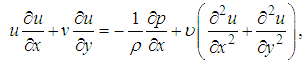 | (17) |
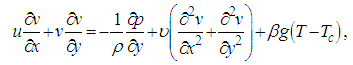 | (18) |
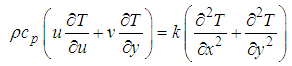 | (19) |
where 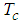 is the temperature of ambient mediumIn the above equations we will describe the velocity components
is the temperature of ambient mediumIn the above equations we will describe the velocity components 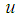 and
and 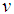 as the derivatives of the stream function
as the derivatives of the stream function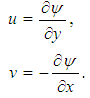 | (20) |
the vorticity equation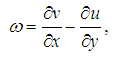 | (21) |
Introduced the following non-dimensional variables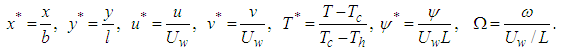 | (22) |
where 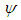 is the stream function,
is the stream function, 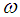 is the vorticity and
is the vorticity and 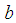 is the weight of the enclosure.The results of the analysis (after dropping the
is the weight of the enclosure.The results of the analysis (after dropping the  -notation) are the stream function equation
-notation) are the stream function equation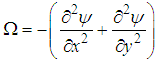 | (23) |
and the vorticity transport equation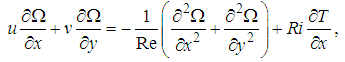 | (24) |
and also, the energy equation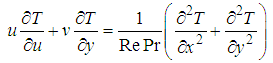 | (25) |
where 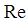 is the Reynolds number,
is the Reynolds number, 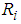 is the Richardson number and
is the Richardson number and 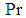 is the Prandtl number.The boundary conditions and initial condition for two enclosure
is the Prandtl number.The boundary conditions and initial condition for two enclosure 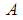 and
and 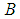 are as follows:
are as follows: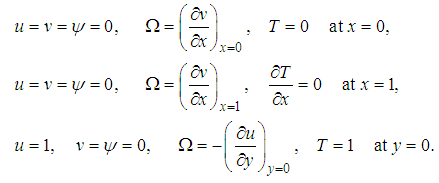 | (26) |
Special cases for the boundary condition:Case 1: Upper wall of enclosure 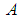
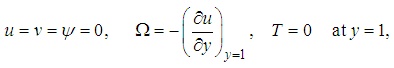 | (27) |
Case 2: Lower wall of enclosure 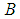
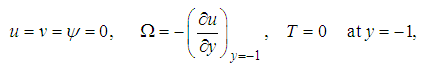 | (28) |
where 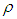 is the fluid density,
is the fluid density, 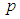 is the pressure,
is the pressure, 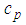 is the specific heat capacity at constant pressure,
is the specific heat capacity at constant pressure, 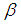 is the volumetric coefficient of thermal expansion,
is the volumetric coefficient of thermal expansion, 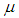 is the fluid viscosity,
is the fluid viscosity, 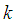 is the thermal conductivity,
is the thermal conductivity, 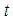 is the time,
is the time, 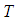 is the temperature and
is the temperature and 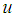 ,
, 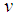 are the fluid velocity components, in the
are the fluid velocity components, in the 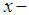 and
and 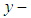 directions, respectively.The aim of the present investigation is to discuss the analytical approach for the steady two-dimensional incompressible and laminar in rectangular domain.ApplicationsChoosing the linear and nonlinear operator defined by
directions, respectively.The aim of the present investigation is to discuss the analytical approach for the steady two-dimensional incompressible and laminar in rectangular domain.ApplicationsChoosing the linear and nonlinear operator defined by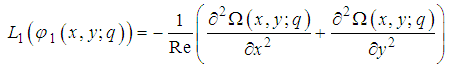 | (29) |
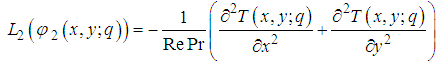 | (30) |
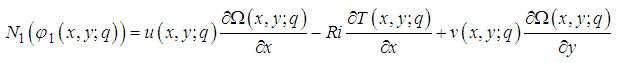 | (31) |
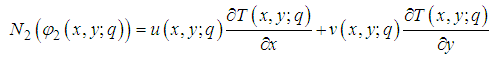 | (32) |
and the stream function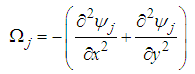 | (33) |
The correspond boundary conditions are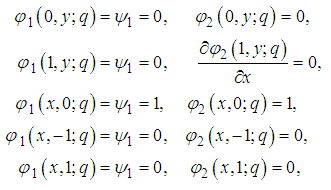 | (34) |
The zeroth order deformation: 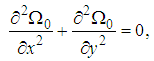 | (35) |
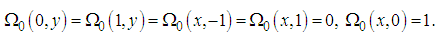 | (36) |
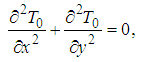 | (37) |
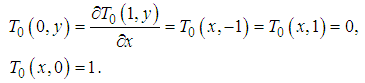 | (38) |
whose solutions are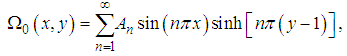 | (39) |
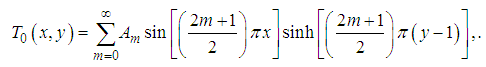 | (40) |
where 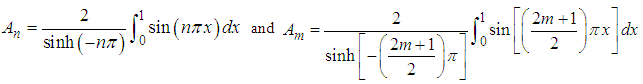 Using equation (39), the stream function (33) becomes
Using equation (39), the stream function (33) becomes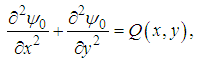 | (41) |
subject to the the boundary conditions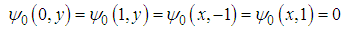 | (42a) |
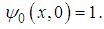 | (42b) |
where 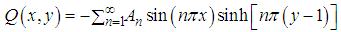 Our first approach to find the stream function is to split problem (41) in two problems that are easier to solve:
Our first approach to find the stream function is to split problem (41) in two problems that are easier to solve: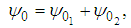 | (43) |
where 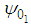 is a particular solution of the stream function and
is a particular solution of the stream function and 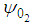 is the solution of the corresponding homogeneous stream function. That is,
is the solution of the corresponding homogeneous stream function. That is,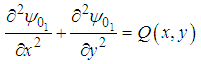 | (44) |
non-homogeneous equation (44) corresponding to the homogeneous boundary condition in (42a) 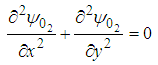 | (45) |
homogeneous equation (45) corresponding to the nonhomogeneous boundary condition in (42b) Using the method of eigenfunction expansion we expand 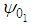 in a series of
in a series of 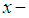 eigenfunctions
eigenfunctions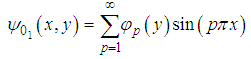 | (46) |
By differentiating (46) twice with respect to 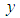 then replacing in (44) we obtain
then replacing in (44) we obtain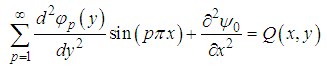 | (47) |
Again, differentiating term-by-term of (46) twice with respect to 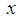 we obtain:
we obtain: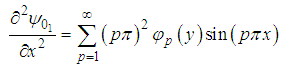 | (48) |
so that equation (47) becomes 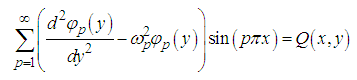 | (49) |
where 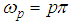 Multiplying equation (49) by
Multiplying equation (49) by 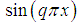 and integrating with respect to
and integrating with respect to 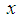 from
from 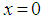 to
to 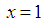 and interchanging the order of summation and integration, we get
and interchanging the order of summation and integration, we get 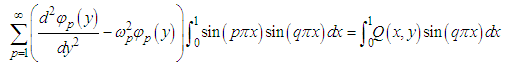 | (50) |
Using the orthogonality property, this equation reduce to 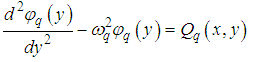 | (51) |
where 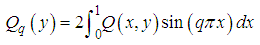 | (52) |
The series (46) satisfy the boundary condition (42a) if 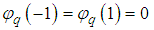 | (53) |
Equation (51) subject to the condition (53) is a second order linear ODE which can be solve by using the method of variation of parameters.The complementary function for the homogeneous function is 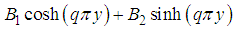 . Taking
. Taking 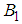 and
and 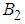 as function of
as function of 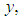 let
let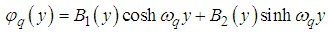 | (54) |
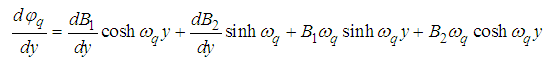 | (55) |
we choose 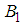 and
and 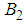 such that
such that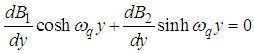 | (56) |
Therefore,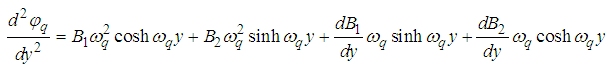 | (57) |
Substituting equations (54) and (57) into equation (51), we obtain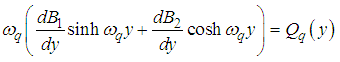 | (58) |
Solving equations (56) and (58) for 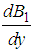 and
and 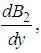 we obtain
we obtain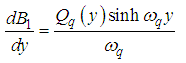 | (59) |
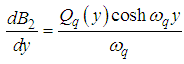 | (60) |
Integrating, we get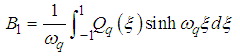 | (61) |
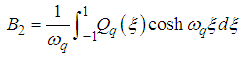 | (62) |
Thus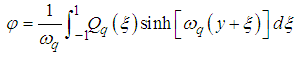 | (63) |
where 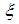 is a dummy variable.Hence, the solution of the nonhomogeneous equation describe by equations (41) and (42a), using the superposition principle is
is a dummy variable.Hence, the solution of the nonhomogeneous equation describe by equations (41) and (42a), using the superposition principle is 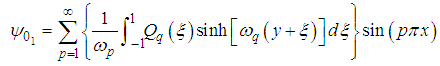 | (64) |
By using the superposition principle, the general solution of equation (45) is found to be 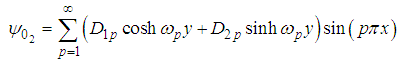 | (65) |
Using the nonhomogeneous boundary condition in (42b) 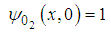 | (66) |
It follows from (66) 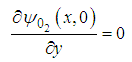 | (67) |
Equation (67) reduces to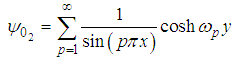 | (68) |
Hence, the series solution of the stream function (41) is 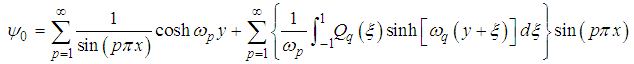 | (69) |
After evaluating the integral, we have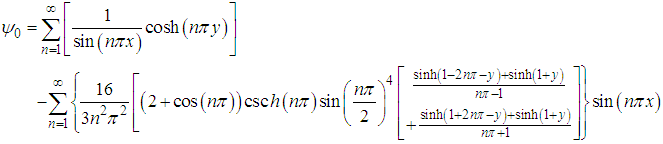 | (70) |
In view of equations (20) and (21), the velocity components are the derivatives of the stream function (70) 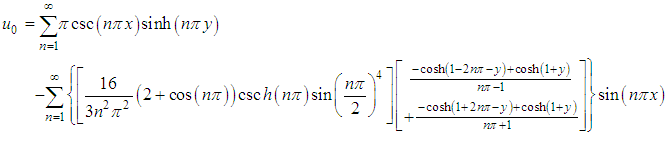 | (71) |
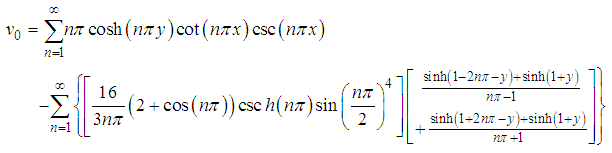 | (72) |
The first order deformation: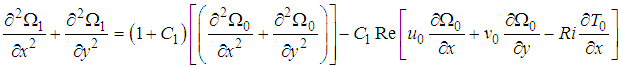 | (73) |
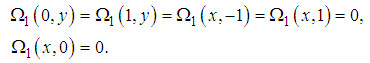 | (74) |
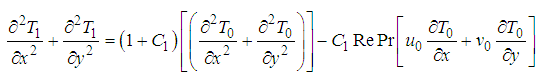 | (75) |
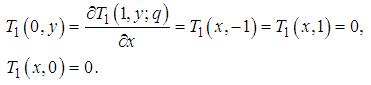 | (76) |
where 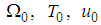 and
and 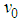 are defined by equations (39), (40), (71), and (72) , respectively.We assume the solutions of equations (73) and (75) of the form
are defined by equations (39), (40), (71), and (72) , respectively.We assume the solutions of equations (73) and (75) of the form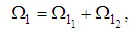 | (77) |
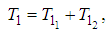 | (78) |
where 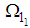 and
and 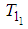 are the particular solutions while
are the particular solutions while 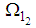 and
and 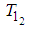 are the solutions of the corresponding homogeneous equations. That is
are the solutions of the corresponding homogeneous equations. That is 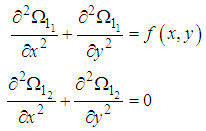 | (79) |
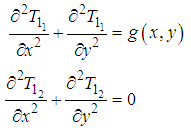 | (80) |
using the method of eigenfunction and variation of parameters the solution of 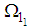 and
and 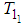 satisfying the homogeneous boundary condition (74) and (76) respectively, are express in the following form the following form
satisfying the homogeneous boundary condition (74) and (76) respectively, are express in the following form the following form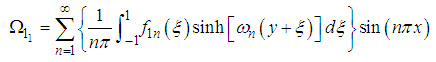 | (81) |
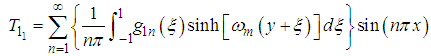 | (82) |
where 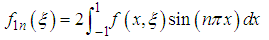 | (83) |
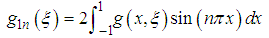 | (84) |
Now, we shall find 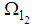 and
and 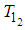 from equation (80) and (82) satisfying
from equation (80) and (82) satisfying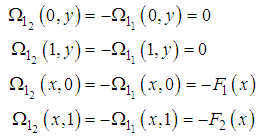 | (85) |
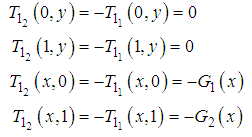 | (86) |
where 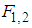 and
and 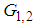 are the only non-zero boundary conditions.The above boundary conditions are obtained by using equations (77) and (78) and the given boundary condition (74) and (76). By using the superposition principle, the general solution of equations (80) and (82) are found
are the only non-zero boundary conditions.The above boundary conditions are obtained by using equations (77) and (78) and the given boundary condition (74) and (76). By using the superposition principle, the general solution of equations (80) and (82) are found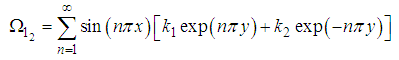 | (87) |
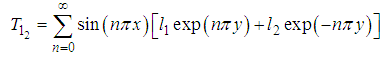 | (88) |
where 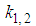 and
and 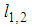 are constants to determined.Now, applying the nonhomogeneous boundary conditions (85) and (86) into equations (87) and (88), respectively, we get, after renaming the constants, the equations
are constants to determined.Now, applying the nonhomogeneous boundary conditions (85) and (86) into equations (87) and (88), respectively, we get, after renaming the constants, the equations 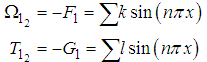 | (89) |
Also, applying homogeneous boundary conditions (85) and (86), equations (87) and (88), respectively can be written as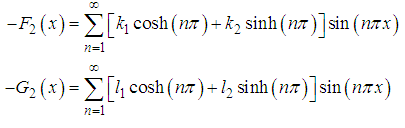 | (90) |
which gives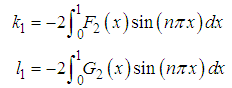 | (91) |
Also, from equations (87) and (88), we have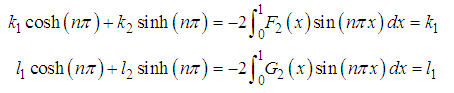 | (92) |
therefore,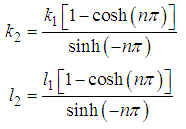 | (93) |
Hence, the series solutions of equations is 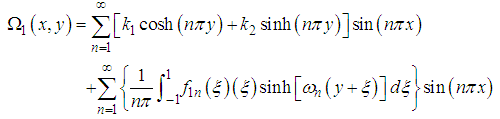 | (94) |
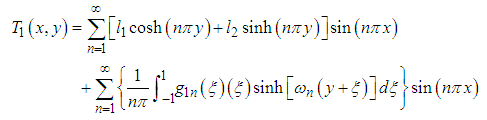 | (95) |
3. Conclusions Remarks
In this paper, an optimal homotopy asymptotic method is applied for solving rectangular enclosures driven by a continuously moving horizontal plate. This procedure is explicit, efficient and has a distinct advantage over usual approximation methods in that the approximate solution obtained here is valid not only for weakly nonlinear equations, but also for strongly nonlinear ones. This approach seems to be useful and can be used to obtain other analytical solutions for other couple flow problems.
References
| [1] | Waheed, M. A. (2009). Mixed convective heat transfer in rectangular enclosures driven by a continuously moving horizontal plate. International Journal of Heat and Mass Transfer, 52(21--22), 5055-5063. |
| [2] | Abu-Nada, E., and Chamkha, A. J. (2010). Mixed convection flow in a lid-driven inclined square enclosure filled with a nanofluid. European Journal of Mechanics - B/Fluids, 29(6), 472-482. |
| [3] | Bhattacharya, M., Basak, T., Oztop, H. F., and Varol, Y. (2013). Mixed convection and role of multiple solutions in lid-driven trapezoidal enclosures. International Journal of Heat and Mass Transfer, 63(0), 366-388. |
| [4] | Teamah, M. A., and El-Maghlany, W. M. (2010). Numerical simulation of double-diffusive mixed convective flow in rectangular enclosure with insulated moving lid. International Journal of Thermal Sciences, 49(9), 1625-1638. |
| [5] | Teamah, M. A., Elsafty, A. F., and Massoud, E. Z. (2012). Numerical simulation of double-diffusive natural convective flow in an inclined rectangular enclosure in the presence of magnetic field and heat source. International Journal of Thermal Sciences, 52(0), 161-175. |
| [6] | Alinia, M., Ganji, D. D., and Gorji-Bandpy, M. (2011). Numerical study of mixed convection in an inclined two sided lid driven cavity filled with nanofluid using two-phase mixture model. International Communications in Heat and Mass Transfer, 38(10), 1428-1435. |
| [7] | Oosthuizen, P. H., and Paul, J. T. (2005). Natural convection in a rectangular enclosure with two heated sections on the lower surface. International Journal of Heat and Fluid Flow, 26(4), 587-596. |
| [8] | Ece, M. C., and Büyük, E. (2006). Natural-convection flow under a magnetic field in an inclined rectangular enclosure heated and cooled on adjacent walls. Fluid Dynamics Research, 38(8), 564-590. |
| [9] | Bocu, Z., and Altac, Z. (2011). Laminar natural convection heat transfer and air flow in three-dimensional rectangular enclosures with pin arrays attached to hot wall. Applied Thermal Engineering, 31(16), 3189-3195. |
| [10] | Kuznetsov, G. V., and Sheremet, M. A. (2010). Numerical simulation of turbulent natural convection in a rectangular enclosure having finite thickness walls. International Journal of Heat and Mass Transfer, 53(1--3), 163-177. |

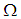 and temperature
and temperature 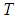 that is
that is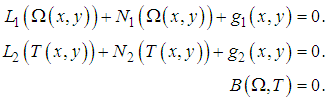
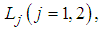 are linear operators,
are linear operators, 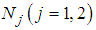 are non-linear operators,
are non-linear operators, 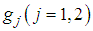 are known function and
are known function and 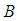 is a boundary operator.Construct an optimal homotopy
is a boundary operator.Construct an optimal homotopy 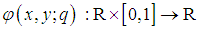 which satisfies the following equations:
which satisfies the following equations: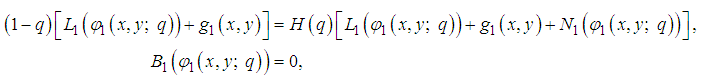
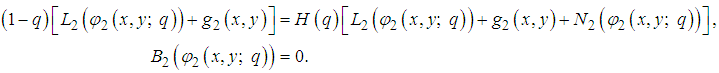
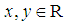 and
and 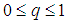 is an embedding parameter,
is an embedding parameter, 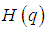 is a nonzero auxiliary function for
is a nonzero auxiliary function for 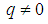 and
and 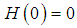 , and
, and 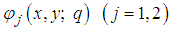 are unknown functionsClearly, when
are unknown functionsClearly, when 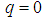 and
and 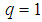 it holds that
it holds that 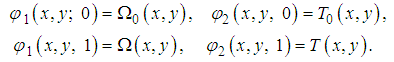
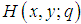 in the form
in the form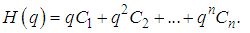
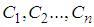 are constants to be determined.Construct a Taylor's series solution of equations (2) and (3) in the form
are constants to be determined.Construct a Taylor's series solution of equations (2) and (3) in the form 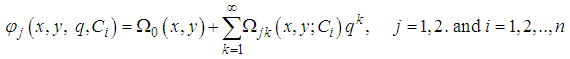
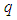 to obtain
to obtain 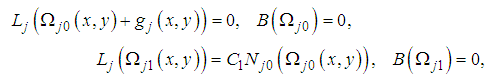
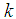 th order equation is defined by
th order equation is defined by 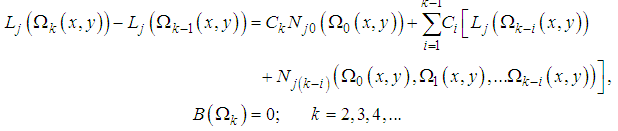
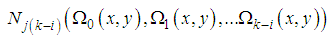 is the coefficient of
is the coefficient of 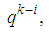 obtained by expanding
obtained by expanding 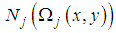 in series with respect to the embedding parameter
in series with respect to the embedding parameter 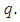
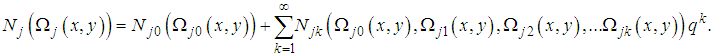
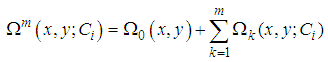
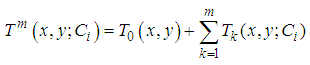
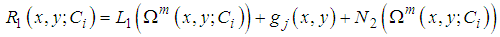
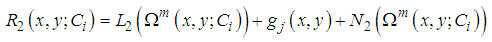
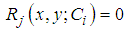 , then (10) and (11) will be the exact solution. Generally such a case will not happen for nonlinear problems, but we can minimize the functional by the method of lease squares
, then (10) and (11) will be the exact solution. Generally such a case will not happen for nonlinear problems, but we can minimize the functional by the method of lease squares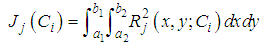
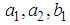 and
and 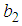 belong to the domain of the problem. Finally, the unknown constants
belong to the domain of the problem. Finally, the unknown constants 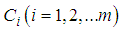 can be optimally identified from the conditions
can be optimally identified from the conditions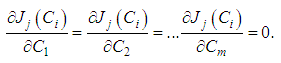
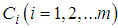 , the approximate solution of equation (10) and (11) are well determined.Statement of the problemIn the present investigation, we consider convective heat transfer and flow in a rectangular enclosure driven by a horizontal wall, the horizontal plate divides the rectangular enclosure into equal halves while being cooled from one horizontal and vertical wall, with the other vertical wall thermally isolated as described by Waheed [1] Figure 1 show the physical configuration.
, the approximate solution of equation (10) and (11) are well determined.Statement of the problemIn the present investigation, we consider convective heat transfer and flow in a rectangular enclosure driven by a horizontal wall, the horizontal plate divides the rectangular enclosure into equal halves while being cooled from one horizontal and vertical wall, with the other vertical wall thermally isolated as described by Waheed [1] Figure 1 show the physical configuration.
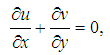
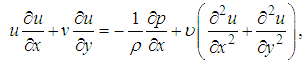
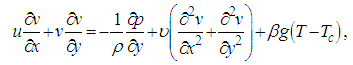
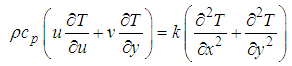
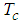 is the temperature of ambient mediumIn the above equations we will describe the velocity components
is the temperature of ambient mediumIn the above equations we will describe the velocity components 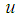 and
and 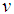 as the derivatives of the stream function
as the derivatives of the stream function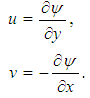
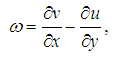
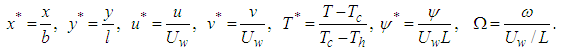
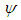 is the stream function,
is the stream function, 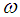 is the vorticity and
is the vorticity and 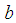 is the weight of the enclosure.The results of the analysis (after dropping the
is the weight of the enclosure.The results of the analysis (after dropping the  -notation) are the stream function equation
-notation) are the stream function equation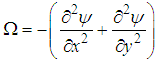
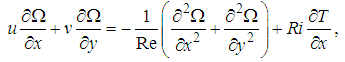
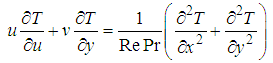
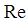 is the Reynolds number,
is the Reynolds number, 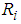 is the Richardson number and
is the Richardson number and 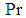 is the Prandtl number.The boundary conditions and initial condition for two enclosure
is the Prandtl number.The boundary conditions and initial condition for two enclosure 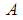 and
and 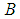 are as follows:
are as follows: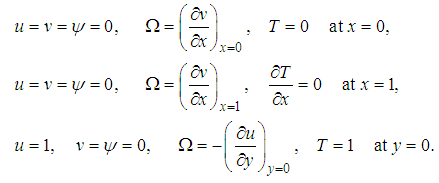
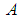
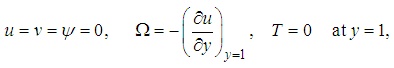
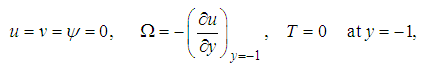
 is the fluid density,
is the fluid density, 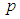 is the pressure,
is the pressure, 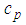 is the specific heat capacity at constant pressure,
is the specific heat capacity at constant pressure, 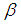 is the volumetric coefficient of thermal expansion,
is the volumetric coefficient of thermal expansion, 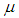 is the fluid viscosity,
is the fluid viscosity, 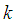 is the thermal conductivity,
is the thermal conductivity, 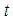 is the time,
is the time, 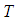 is the temperature and
is the temperature and 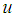 ,
, 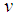 are the fluid velocity components, in the
are the fluid velocity components, in the 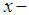 and
and 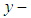 directions, respectively.The aim of the present investigation is to discuss the analytical approach for the steady two-dimensional incompressible and laminar in rectangular domain.ApplicationsChoosing the linear and nonlinear operator defined by
directions, respectively.The aim of the present investigation is to discuss the analytical approach for the steady two-dimensional incompressible and laminar in rectangular domain.ApplicationsChoosing the linear and nonlinear operator defined by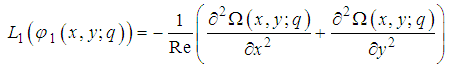
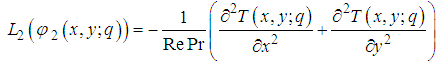
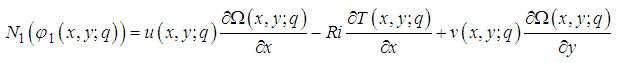
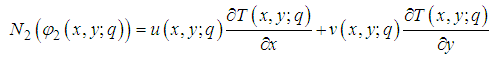
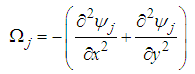
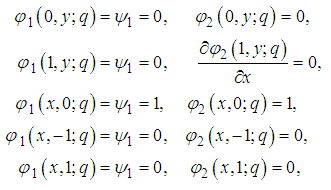
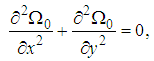
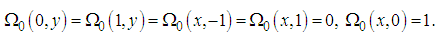
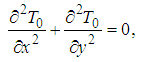
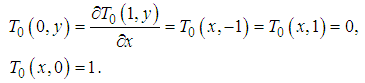
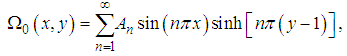
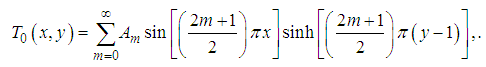
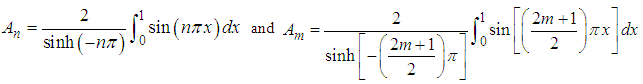 Using equation (39), the stream function (33) becomes
Using equation (39), the stream function (33) becomes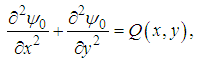
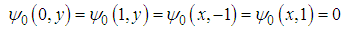
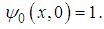
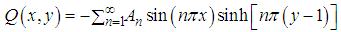 Our first approach to find the stream function is to split problem (41) in two problems that are easier to solve:
Our first approach to find the stream function is to split problem (41) in two problems that are easier to solve: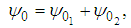
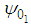 is a particular solution of the stream function and
is a particular solution of the stream function and 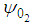 is the solution of the corresponding homogeneous stream function. That is,
is the solution of the corresponding homogeneous stream function. That is,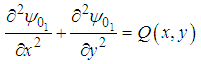
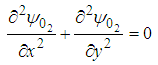
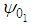 in a series of
in a series of 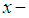 eigenfunctions
eigenfunctions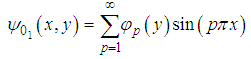
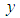 then replacing in (44) we obtain
then replacing in (44) we obtain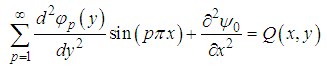
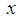 we obtain:
we obtain: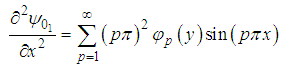
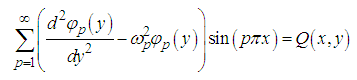
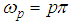 Multiplying equation (49) by
Multiplying equation (49) by 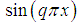 and integrating with respect to
and integrating with respect to 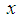 from
from 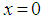 to
to 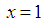 and interchanging the order of summation and integration, we get
and interchanging the order of summation and integration, we get 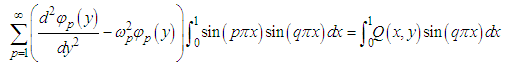
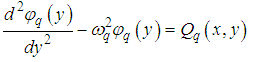
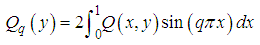
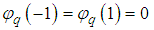
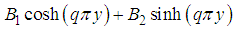 . Taking
. Taking 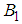 and
and 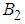 as function of
as function of 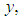 let
let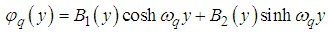
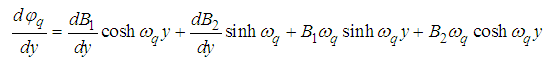
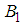 and
and 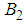 such that
such that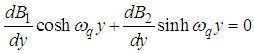
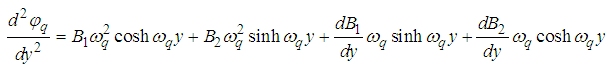
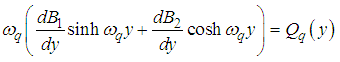
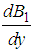 and
and 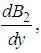 we obtain
we obtain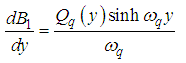
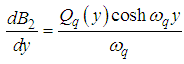
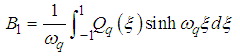
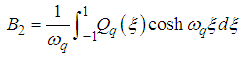
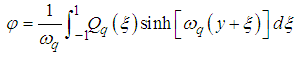
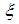 is a dummy variable.Hence, the solution of the nonhomogeneous equation describe by equations (41) and (42a), using the superposition principle is
is a dummy variable.Hence, the solution of the nonhomogeneous equation describe by equations (41) and (42a), using the superposition principle is 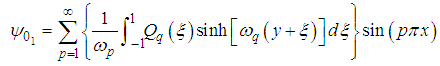
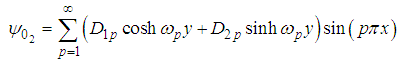
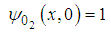
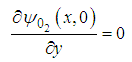
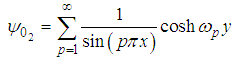
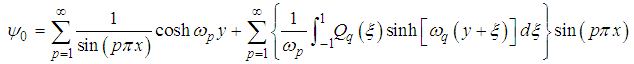
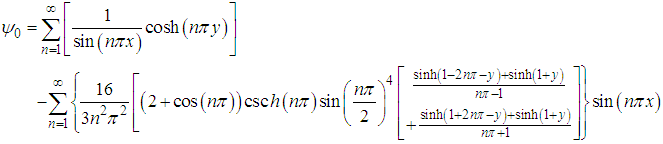
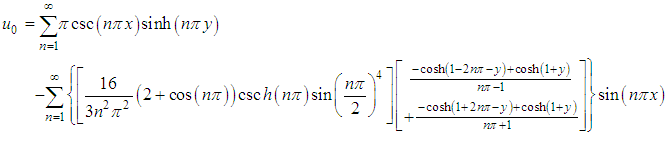
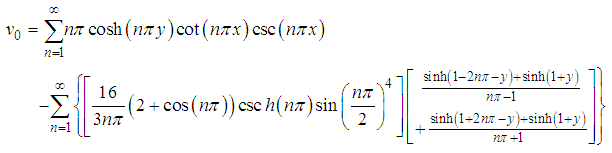
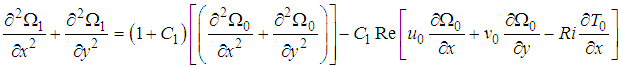
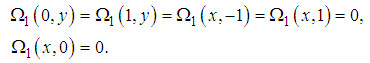
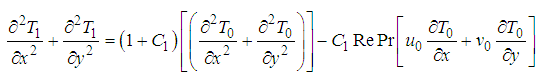
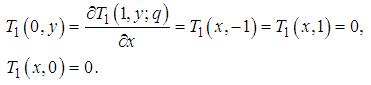
 and
and  are defined by equations (39), (40), (71), and (72) , respectively.We assume the solutions of equations (73) and (75) of the form
are defined by equations (39), (40), (71), and (72) , respectively.We assume the solutions of equations (73) and (75) of the form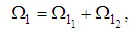
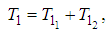
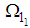 and
and 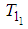 are the particular solutions while
are the particular solutions while 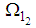 and
and 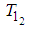 are the solutions of the corresponding homogeneous equations. That is
are the solutions of the corresponding homogeneous equations. That is 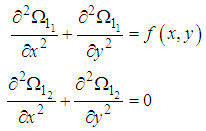
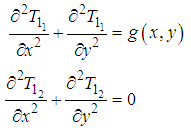
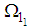 and
and 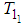 satisfying the homogeneous boundary condition (74) and (76) respectively, are express in the following form the following form
satisfying the homogeneous boundary condition (74) and (76) respectively, are express in the following form the following form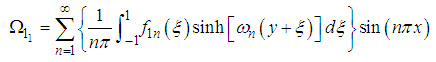
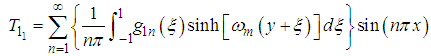
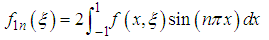
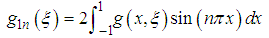
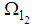 and
and 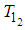 from equation (80) and (82) satisfying
from equation (80) and (82) satisfying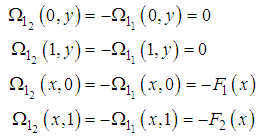
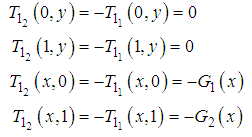
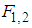 and
and 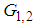 are the only non-zero boundary conditions.The above boundary conditions are obtained by using equations (77) and (78) and the given boundary condition (74) and (76). By using the superposition principle, the general solution of equations (80) and (82) are found
are the only non-zero boundary conditions.The above boundary conditions are obtained by using equations (77) and (78) and the given boundary condition (74) and (76). By using the superposition principle, the general solution of equations (80) and (82) are found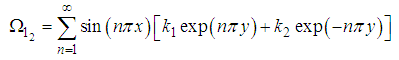
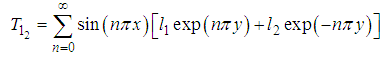
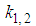 and
and 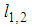 are constants to determined.Now, applying the nonhomogeneous boundary conditions (85) and (86) into equations (87) and (88), respectively, we get, after renaming the constants, the equations
are constants to determined.Now, applying the nonhomogeneous boundary conditions (85) and (86) into equations (87) and (88), respectively, we get, after renaming the constants, the equations 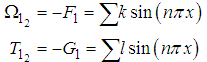
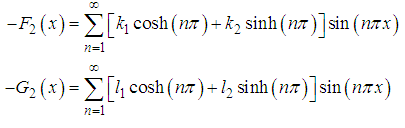
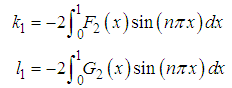
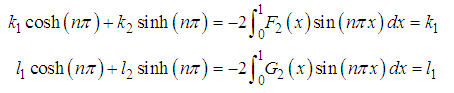
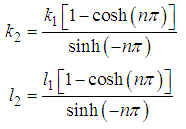
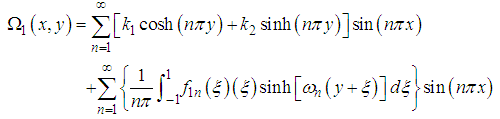
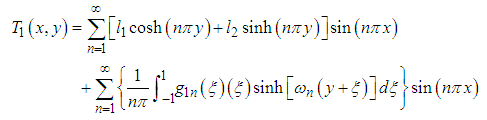
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML