-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Science and Technology
p-ISSN: 2163-2669 e-ISSN: 2163-2677
2013; 3(4): 118-122
doi:10.5923/j.scit.20130304.04
Thermodynamics of the Solvation of Potassium Thiocyanate in Mixed EtOH-H2O Solvents at 301.15 K
Esam A. Gomaa1, Elsayed M. Abou Ellef2
1Chemistry Department, Faculty of Science, Mansoura University, 35516, Mansoura, Egypt
2Delta Higher Instituts for Engineering and Technology, Basic Science Department, Mansoura, Egypt
Correspondence to: Esam A. Gomaa, Chemistry Department, Faculty of Science, Mansoura University, 35516, Mansoura, Egypt.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The Gibbs free energies as very important thermodynamic property were evaluated for potassium thiocyanate (KSCN) in mixed ethanol (EtOH-H2O) solvents at 301.15 K from the experimental solubility measarments. The ratio of the ionic radii between potassium and thiocyanate ions was used to divide the total Gibbs free energy of the salt into its individual contribution in the mixtures used. Libration Gibbs free energy associated with moving KSCN in standard gas state to standard state in solution was evaluated according to specific cycle for the solvation process using the solubility products. Also the lattice energy for solid KSCN (Cr) was calculated and used for further evaluation. The conventional Gibbs free energies for the cation (K+) and anion (SCN-) were estimated theoretically and also the Gibbs free energy of (SCN-) gas was evaluated and all values were discussed. The present work is concerned with relative(conventional) and absolute Gibbs free energies of the solvation of ions used.
Keywords: Gibbs Free Energies, potassium Thiocyanate, conventional Free Energies, solubility Measurements, thermodynamic Solvation Energies
Cite this paper: Esam A. Gomaa, Elsayed M. Abou Ellef, Thermodynamics of the Solvation of Potassium Thiocyanate in Mixed EtOH-H2O Solvents at 301.15 K, Science and Technology, Vol. 3 No. 4, 2013, pp. 118-122. doi: 10.5923/j.scit.20130304.04.
Article Outline
1. Introduction
- For neutral species experimental solvation Gibbs free energies have been tabulated large number of solutes in both aqueous[1-7] and non-aqueous solvents[7, 8]. Typically, these solvation: free energies are determined experimentally [8] and their uncertainty is relatively low
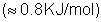 [9].Determining accurate values for the Gibbs free energies of ionic solutes like KSCN is important than that of neutral solutes. Understanding the partion of single ions between different liquid phases is important in many areas of biology. For example, the electrical signals sent by nerve cells are activated by changes in cell potential that are caused by the movement of various ions across the neuronal membrane[10]. The division of thermodynamic Gibbs free energies of solvation of electrolytes into ionic constituents is conventionally accomplished by using the single ion solvation Gibbs free energy of one reference ion, conventionally, the proton, to set the single ion scales[11, 12]. The aim of this work is to estimate the single ion Gibbs free energies for K+ & SCN- ions in mixed EtOH-H2O solvents at 301.15 K.Sums of solvation free energies of cations and anions are well defined through the use of thermochemical cycles involving calorimetric or electrochemicalmeasurnents[13-17]. A number of different extra thermodynamic approximations have been used[18-25] for partition the sums of cation and anion Gibbs free energies into single ion contribution. Single ion thermodynamics is important for studing the experimental and theoretical behavior of different salts in various solvents. Single ionthermodynamics are necessary for studying ionic conduction, solvent rotation solvent reorientation, solvent geometric distortion, solvent electronic polarization and electronic conduction[6]. The aim of this work is to provide the theoretical and experimental researchers with different ions data which help in explanation of different electrical properties.
[9].Determining accurate values for the Gibbs free energies of ionic solutes like KSCN is important than that of neutral solutes. Understanding the partion of single ions between different liquid phases is important in many areas of biology. For example, the electrical signals sent by nerve cells are activated by changes in cell potential that are caused by the movement of various ions across the neuronal membrane[10]. The division of thermodynamic Gibbs free energies of solvation of electrolytes into ionic constituents is conventionally accomplished by using the single ion solvation Gibbs free energy of one reference ion, conventionally, the proton, to set the single ion scales[11, 12]. The aim of this work is to estimate the single ion Gibbs free energies for K+ & SCN- ions in mixed EtOH-H2O solvents at 301.15 K.Sums of solvation free energies of cations and anions are well defined through the use of thermochemical cycles involving calorimetric or electrochemicalmeasurnents[13-17]. A number of different extra thermodynamic approximations have been used[18-25] for partition the sums of cation and anion Gibbs free energies into single ion contribution. Single ion thermodynamics is important for studing the experimental and theoretical behavior of different salts in various solvents. Single ionthermodynamics are necessary for studying ionic conduction, solvent rotation solvent reorientation, solvent geometric distortion, solvent electronic polarization and electronic conduction[6]. The aim of this work is to provide the theoretical and experimental researchers with different ions data which help in explanation of different electrical properties.1.1. Relative and Conventional Solvation Free Energies of Ions
- The Gibbs solvation free energies of ions are often tabulated as relative free energies by setting the free energy of some reference ion equal zero[26]. Proton was chosen as reference ion. For ions, this result in a set of conventional free energies of solvation that the cations are shifted from their absolute values by the value for the absolute Gibbs solvation free energy of the proton.The conventional Gibbs free energies of solvation for anions that are shifted by equal amount in the opposite direction.
1.2. Conventional Gibbs Free Energies from Reduction Potentials
- In the present article relative (conventional) solvation free energies of ions and ion-solvent interaction have been determined using combination of experimental and theoretical free energy of formation.When the convention for the absolute Gibbs free energy of the proton is followed, the solution phase energy change anociated with the half cell for reduction of hydrogen gas is equal to zero. Reduction potentials following this convenstion for hydrogen electrode are referred as standard reduction potentials. From the half cell reaction for the reduction of metal cation to crystalline phase and the half reduction reaction of hydrogen gas, the redox reaction can be illustrated through the use of thermochemical cycle[12]. This last procedure can be used to estimate the gas free energy of formation for SCN- ion, to explain the ionic behaviour.
2. Experimental
- Potassium thiocyanate (KSCN) from Griffin & George Co. and ethanol (EtOH) from Merck Co. were used. Saturated solutions of KSCN were prepared by dissolving different amounts in closed test tubes containing different EtOH-H2O mixtures. These mixtures were then saturated with nitrogen gas as inert atmosphere. The tubes were placed in a shaking thermostat (Model Gel) for a period of four days till equilibrium reached. The solubility of KSCN in each mixture was measured gravimetrically by evaporating 1 ml of the saturated solution in small cups using I. R. lamp. The measurements were done by three readings for each solution at 301.15 K.
3. Results and Discussion
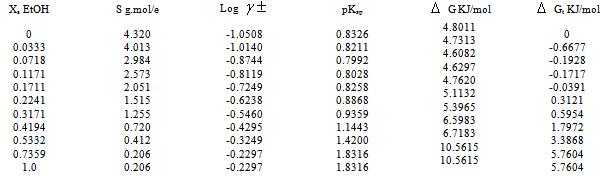
- The molar solubility (s) for KSCN at 301.15 K was measured gravimetrically with average of the second number after common in water, ethanol (EtOH) and their mixtures. The solubility values for KSCN at cited in Table (1). The (s) value in water agreed well with that in literature values[27]. The activity coefficients were calculated by the use of Debye-Hückel equation[28, 29].
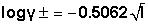 | (1) |
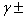 ) were tabulated also in Table (1). The solubility product was calculated by the use of equation (2)[30].
) were tabulated also in Table (1). The solubility product was calculated by the use of equation (2)[30]. | (2) |
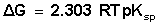 | (3) |
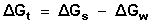 | (4) |
|
|
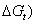 increase in negativity by increasing the mole fraction of EtOH in the mixed EtOH-H2O solvents. This is due to more solvation behaviour in the mixed solvents than that in water (see Fig. 1).
increase in negativity by increasing the mole fraction of EtOH in the mixed EtOH-H2O solvents. This is due to more solvation behaviour in the mixed solvents than that in water (see Fig. 1).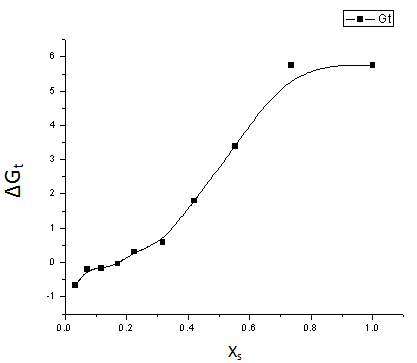 | Figure 1. Gibbs free energies of transfer for KSCN (∆Gt) versus the mole fraction of EtOH (Xs) at 301.15 K |
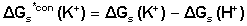 | (5) |
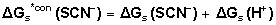 | (6) |
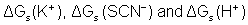 are the Gibbs free energies of solvation for potassium, thiocyanate and proton in solvents.From the mean values of proton solvation free energies in water and othen solvents in literature[12, 35, 36], relation between these values and the diameter for each solvent taken from Kim work[37] straight line was obtained. From this line the proton solvation free energies in pure water and EtOH were obtained and found to be 1523 and 1486.91 KJ/mol, respectively multiplying each value by its mole fraction in the mixture and then sum the results. The mixed solvent proton free energies were obtained and their values are given in Table (2). Apply equation (5) and (6) we get the conventional Gibbs free energies for the cation and the anion, their values are given also in Table (2). Cation conventional free energy values are negative indicating exothermic character and anion values are positive indicating endothermic character. Both values increase with increase in the mole fraction of EtOH due to more solvation and the sum of them gives the values for the neutral salt.
are the Gibbs free energies of solvation for potassium, thiocyanate and proton in solvents.From the mean values of proton solvation free energies in water and othen solvents in literature[12, 35, 36], relation between these values and the diameter for each solvent taken from Kim work[37] straight line was obtained. From this line the proton solvation free energies in pure water and EtOH were obtained and found to be 1523 and 1486.91 KJ/mol, respectively multiplying each value by its mole fraction in the mixture and then sum the results. The mixed solvent proton free energies were obtained and their values are given in Table (2). Apply equation (5) and (6) we get the conventional Gibbs free energies for the cation and the anion, their values are given also in Table (2). Cation conventional free energy values are negative indicating exothermic character and anion values are positive indicating endothermic character. Both values increase with increase in the mole fraction of EtOH due to more solvation and the sum of them gives the values for the neutral salt. 3.1. Libration Gibbs Free Energies for KSCN in Mixed EtOH-H2O Solvents
- The libration Gibbs free energies for KSCN in mixed EtOH-H2O solvents at 301.15 K were calculated following cycle 1 (thermochemical cycle 1) as done before[12] for silver salts following solubility product concept.
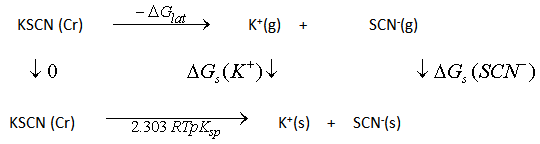 | Thermochemical cycle 1. (cycle 1) |
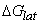 is the lattice free energy, (g) and (s) denote the gas and solution cases. The lattice energy was calculated following Bartlett’s relationship, equation (7)[38].
is the lattice free energy, (g) and (s) denote the gas and solution cases. The lattice energy was calculated following Bartlett’s relationship, equation (7)[38].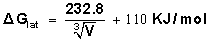 | (7) |
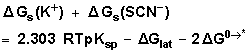 | (8) |
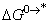 , the free energy change associated with moving KSCN from standard gas phase of 1 atmosphere to solution phase. This free energy change has been referred to as “compression” work of the gas or libration free energy.
, the free energy change associated with moving KSCN from standard gas phase of 1 atmosphere to solution phase. This free energy change has been referred to as “compression” work of the gas or libration free energy. 3.2. Conventional Free Energies from Reduction Potentials
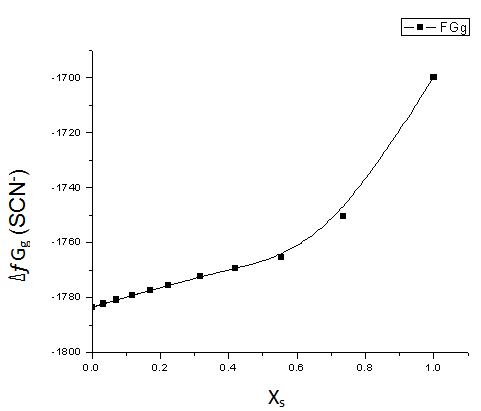 | Figure 2. Relation between 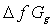 (SCN-) against the mole fraction of EtOH (XS) at 301.15 K (SCN-) against the mole fraction of EtOH (XS) at 301.15 K |
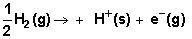 | (9) |
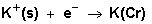 | (10) |
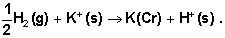 | (11) |
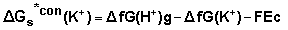 | (12) |
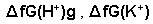 are the gas free energy of formation for H+ and K+ ions. Faraday’s constant = 23.061 Kcal/mol and Ec is the standard reduction potential of K+
are the gas free energy of formation for H+ and K+ ions. Faraday’s constant = 23.061 Kcal/mol and Ec is the standard reduction potential of K+ 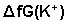 is difficult to evaluate because of the lack of exact
is difficult to evaluate because of the lack of exact  value.
value.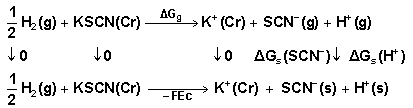 | Thermochemical cycle 2. (cycle 2) |
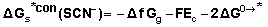 | (13) |
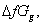 gas free energies for the anion SCN- were estimated in the mixed EtOH-H2O solvents and their values are given in Table (5) and Fig. (2). The
gas free energies for the anion SCN- were estimated in the mixed EtOH-H2O solvents and their values are given in Table (5) and Fig. (2). The 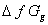 values increase by increasing the mole fraction of EtOH favoring less solvation.
values increase by increasing the mole fraction of EtOH favoring less solvation.
|
4. Conclusions
- This work gives a lot of data for single ion thermodynamic free energies for potassium and thiocyante ions in mixed ethanol water solvents which help in discussing the preferentional solvation in the used solvents. Also the data can help for studying other salts having the same common ions used.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML