-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Science and Technology
p-ISSN: 2163-2669 e-ISSN: 2163-2677
2013; 3(1): 24-32
doi:10.5923/j.scit.20130301.03
An Optimized ANN Approach for Cutting Forces Prediction in AISI 52100 Bearing Steel Hard Turning
Souâd Makhfi 1, 2, Raphaël Velasco 1, Malek Habak 1, Kamel Haddouche 2, Pascal Vantomme 1
1Laboratoire de Recherche des Technologies Industrielles. Université Ibn Khaldoun de Tiaret, B.P. 78, 14000, Tiaret Algérie
2Laboratoire des Technologies Innovantes E.A. 3899, Université de Picardie Jules Verne, avenue des Facultés, Le Bailly, 80025, Amiens Cedex 1, France
Correspondence to: Raphaël Velasco , Laboratoire de Recherche des Technologies Industrielles. Université Ibn Khaldoun de Tiaret, B.P. 78, 14000, Tiaret Algérie.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Cutting forces are classified among the important technological parameters in machining processes due to their significant impacts on product quality. A large number of interrelated machining parameters have a great influence on cutting forces so it is quite difficult to develop a proper theoretical model to describe efficiently and globally a machining process.In this paper, an artificial neural network (ANN) model is then proposed to predict cutting force components during hard turning of an AISI 52100 bearing steel using CBN cutting tools. This study is based on an experimental dataset of cutting forces measured during hard turning. Cutting speed (Vc, m/min), feed rate (f, mm/rev), cutting depth (ap, mm) and workpiece hardness (HRc, MPa) are taken as input parameters in the ANN model, while the three cutting force components (feed force Fa, radial force Fr and cutting force Ft, in N) are the output data.The ANN model consists of a multi-layer feed-forward, trained by a back-propagation (BP) algorithm. The influence of a double hidden layer (instead of a single hidden layer) is investigated, and a comparison is carried out between Bayesian Regularization associated with Levenberg–Marquardt algorithm (BR/LM) and simple Levenberg–Marquardt algorithm (LM). A various number of neurons in the hidden layer are also tested.The best prediction accuracy is found while using a feed forward single hidden layer ANN trained by BR/LM and using a sigmoid activation function on hidden layer and a linear one on output layer. The best structure uses 11 neurons in the hidden layer and average prediction errors on the testing dataset are given: 11.47% on Fa, 11.47% on Fr and 6.17% on Ft.
Keywords: Hard Turning, Artificial Neural Network, Cutting Parameters Influence, Cutting Forces Prediction
Cite this paper: Souâd Makhfi , Raphaël Velasco , Malek Habak , Kamel Haddouche , Pascal Vantomme , An Optimized ANN Approach for Cutting Forces Prediction in AISI 52100 Bearing Steel Hard Turning, Science and Technology, Vol. 3 No. 1, 2013, pp. 24-32. doi: 10.5923/j.scit.20130301.03.
Article Outline
1. Introduction
- Machining is a major process in manufacture used especially to finish mechanical parts. Costs of these operations and final products quality are highly constrained to take into account an increasingly competitive environment, where investors require higher returns on their investments. Hard machining processes produce high cutting forces and temperatures that affect some cutting process parameters, such as dynamic stability, tool wear, work piece surface integrity, geometrical dimensions. Cutting forces modeling is so necessary, as it permits to characterize material machinability, to get some knowledge on the power required during machining ([1]), to monitor tool wear ([2]), to predict surface roughness and more ([3]). Cutting forces are related to various process parameters ([4]) such as tool material, workpiece properties and cutting conditions (i.e. feed rate, cutting speed, cutting depth,…) ([5]). It is then difficult to provide an accurate theoretical model to describe complex machining processes such as milling and turning.Artificial neural network (ANN) approach is routinely considered as an accurate and powerful tool for machining process modeling, as it permits to save much time and money generally spent in experimental procedures. A large amount of works have been carried out on forces modeling which have shown that ANN approach is more accurate and faster than many other analytical and numerical cutting force modeling methods. In the working conducted in[6], an approach for cutting forces modeling has been developed, based on feed-forward multi-layer neural networks trained by BP algorithm, and applied to experimental machining data. Szecsi has investigated the effect of two of the main parameters which influence error convergence: learning rate η and momentum term α. While the used analytical model gives an average prediction error of 9.5% on cutting forces, his neural network provides predictions in training with an average error of 3.5%. In[7], Zuperl and Cus have investigated supervised ANN approach to estimate forces generated during end milling process. They have found that the radial basis network requires more neurons than the standard feed forward neural network with BP learning rule and that feed forward neural network gives more accurate results, but takes 70% much time. In milling, using a multi-layer perceptron with BP training method provides a neural network whose error in training is under 2% for all the three force components, and under 4% in testing. As a comparison, an 11% average error is found using analytical methods. In[8], Hao et al. have introduced a cutting force prediction model for self-propelled rotary tool (SPRT). Two types of analyses are presented: simple BP algorithm and hybrid BP algorithm associated with genetic algorithm (GA–BP). Additionally, they have investigated learning rate lr, which controls the adaptation speed of connection weights between neurons, and the momentum rate m, that takes into account the rate of last connection weights changes. A comparison led on the two numerical models shows that GA–BP network predicts SPRT cutting forces more accurately than BP network during training, which is very important for real-time control. Finally, Aykut et al. have tried in[9] to predict cutting forces in asymmetric milling processes using ANNs. Network training has been performed using scaled conjugate gradient (SCG) and feed-forward BP algorithm. Main average percentage errors (APEs) between experimental and numerical Fx, Fy and Fz values have been found around 2% in training and 10% in testing.Furthermore, some authors have also used opportunities provided by ANN algorithms to predict material behavior in machining: Li et al. has developed in[10] a hybrid model based on an analytical approach using Oxley’s theory combined with a neural network model, in order to predict first cutting forces, temperature in the chip region and chip geometry and then to evaluate workpiece surface roughness, tool wear and chip break ability. They have found errors under 5% on tool wear prediction and 20% on surface roughness and chip breaking ability. Özel and Karpat have compared in[11] exponential regression models and neural network models for tool flank wear and surface roughness predictions during AISI H-13 and AISI 52100 hard turning. As regression models give as good results as ANN models for tool wear prediction, they have found it ineffective to predict surface roughness compared to ANN. At last, Umbrello et al. have developed in[12] a numerical model based on an ANN approach to predict residual stress profile in hard turning of AISI 52100 bearing steel (HRc between 50 and 64). They have especially investigated the optimal number of neurons in the hidden layer and then optimized their model using a hybrid finite element ANN approach ([13]). As a result, their model has given satisfactory results showing a prediction error ranging between 4 and 10%.In the present study, an ANN approach is proposed to predict cutting force components in hard turning: feed force Fa, radial force Fr and cutting force Ft.
1.1. Experimental Background
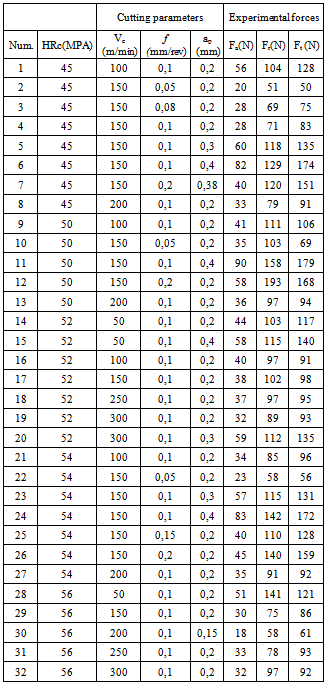
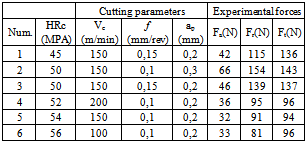
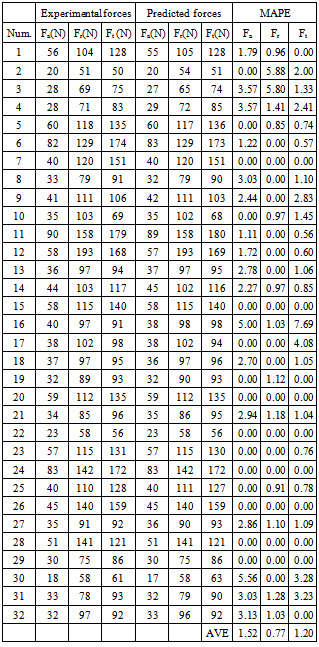
- This numerical work is based on a dataset provided by experimental hard turning of AISI 52100 steel using CBN cutting tools ([14]).As shown on Table 1 and 2, three cutting force components have been experimentally determined for 38 different material hardness and cutting condition combinations (cutting speed Vc, feed rate f, cutting depth ap): the first 32 mentioned on Table 1 are used to train the network and the other 6 are testing conditions (Table 2). The main objective is then to develop an ANN model to properly predict cutting condition influence on cutting forces during this hard turning. This model will of course be valuable in the same ranges as training cutting conditions.
|
|
1.2. Neural Network Modeling
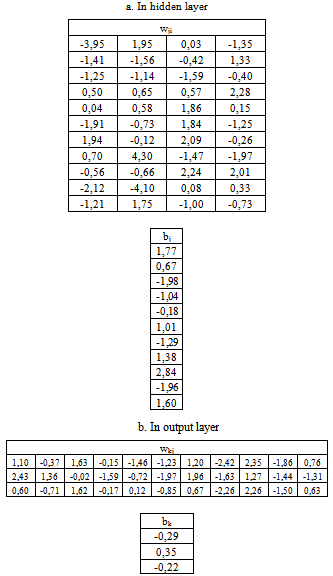
- An artificial neural network (Figure 2) consists of simple processors called neurons which are interconnected. This hierarchical network structure has an input layer receiving data e from the outside and an output layer which sends final information to users. In the middle, hidden layers have no direct contact with the environment.As it has proved its efficiency for approaching non-linear functions ([15]), only BP algorithm has been used for the neural network training. Using notations given on Figure 2, output response is calculated as follow (eq. 1), ([16]):
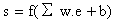 | (1) |
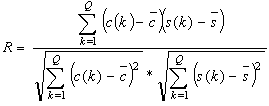 | (2) |
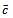 and
and 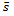 are mean target and output values.● Mean absolute percentage error (MAPE) (eq. 3)
are mean target and output values.● Mean absolute percentage error (MAPE) (eq. 3)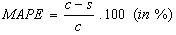 | (3) |
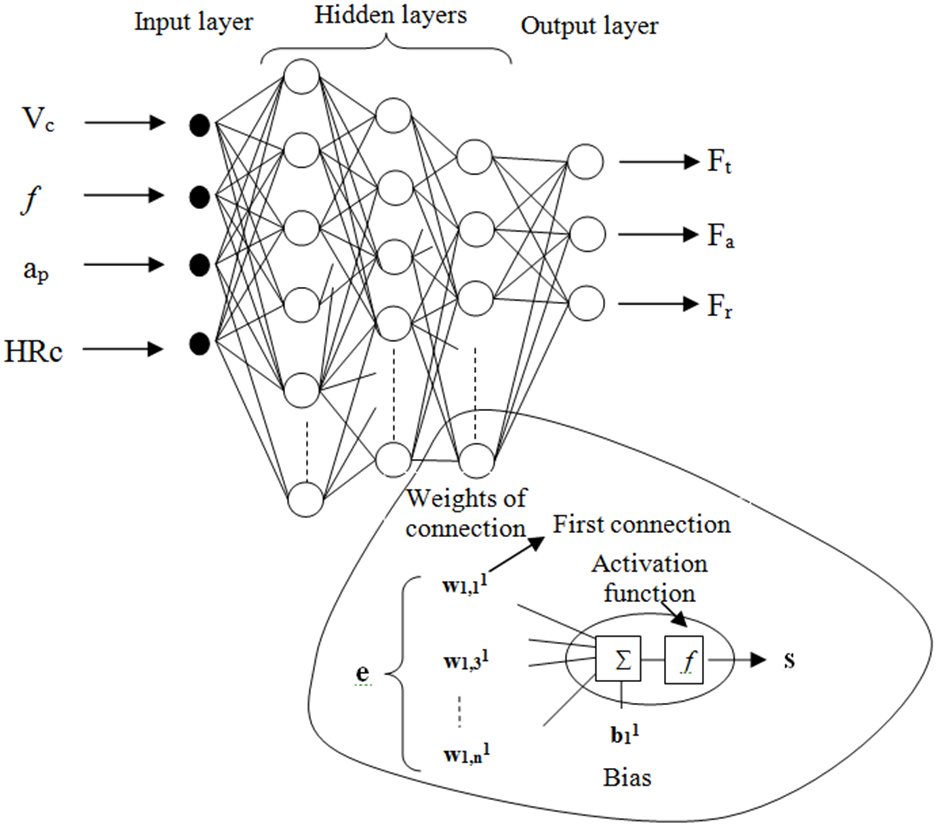 | Figure 2. ANN Multi-layer feed-forward structure |
2. Optimal Choice of an ANN Model
- This study is not only focused on its main objective, namely the development of an ANN model to properly predict cutting condition influence on cutting force components. Some major parameters used in the final ANN model have first been optimized:● The type of activation functions in hidden and output layers● The number of hidden layers● The type of training algorithm (Levenberg–Marquardt (LM) or Levenberg–Marquardt using BayesianRegularization (BR/LM) ([18])● The number of neurons in the hidden layerIn all the following cases, ANNs training are performed on 32 experimental cutting results (Table 1) and their generalization capacities are evaluated on 6 further test data (Table 2), that have of course not been used in training. In each case, input and target values are normalized in the range[-1 -1] to perform an efficient training ([19]).Two activation functions need first to be chosen: one applied in hidden layers and the second used in output layer to determine on the one hand the appropriate number of hidden neurons and on the other hand output values. Table 3 illustrates results of a preliminary analysis: it gives linear regression coefficients obtained in training (R-training) using two couples of activation functions for a various number of hidden neurons:● Sigmoid function
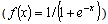 in hidden layer and Linear function (
in hidden layer and Linear function (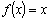 ) in output layer (S.L.)● Sigmoid function in hidden layer and Sigmoid function in output layer (S.S.)
) in output layer (S.L.)● Sigmoid function in hidden layer and Sigmoid function in output layer (S.S.)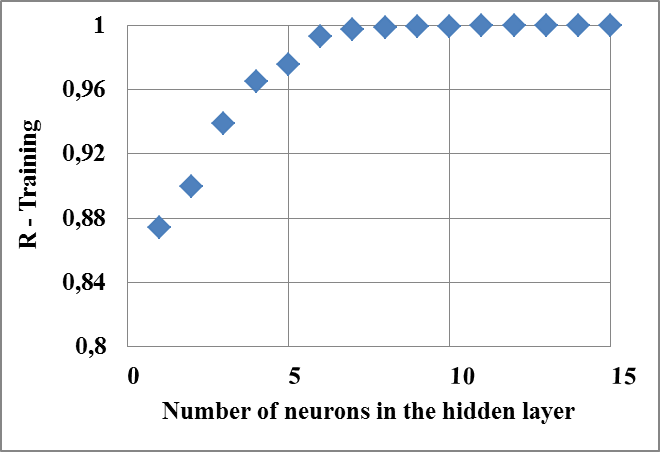 | Figure 3. R-training variation with the number of hidden neurons (in a single hidden layer configuration) |
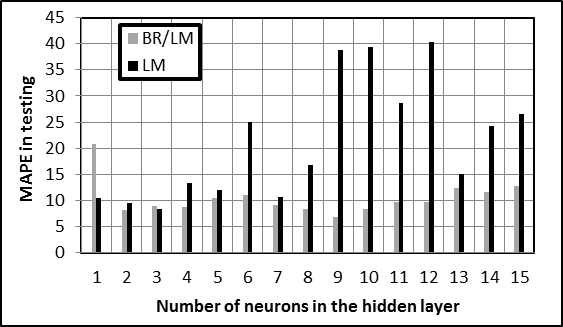 | Figure 4. MAPE values in testingwith the number of hidden neurons |
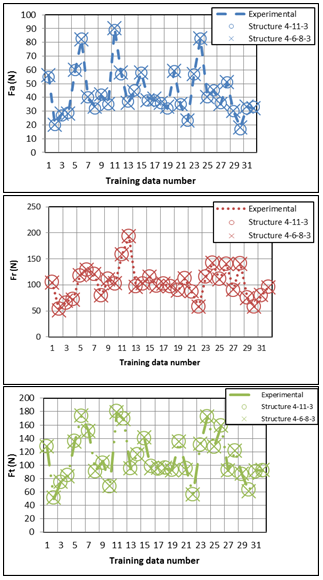 | Figure 5. Experimental and predicted cutting force components for ANN structures 4-11-3 and 4-6-8-3 |
3. Prediction of Cutting Force Components
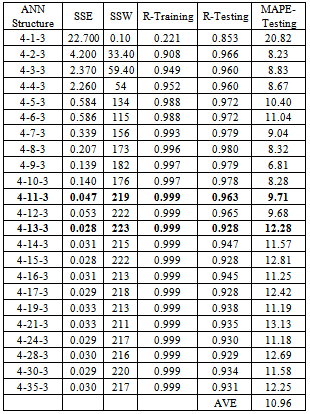
- As explained in introduction, experimental cutting force components have been determined for 38 cutting conditions in which 32 have been used to train the ANN. In order to define the best structure, a various number of neurons in the hidden layer have been tested, from 1 to 35. To evaluate accuracy of the selected structure, cutting force components are calculated for the 6 additional cutting conditions. It can be noticed that testing cutting conditions have to be in the same ranges that the ones used in training.A key point in the choice of the best ANN structure is the selection of statistical criteria. It is not efficient to limit the study to one criterion. So five representative criteria have been calculated for each structure and representative results have been collected in Table 4:● SSE and SSW in training● Linear regression coefficients R in training and testing● MAPE in testing
|
 | (4) |
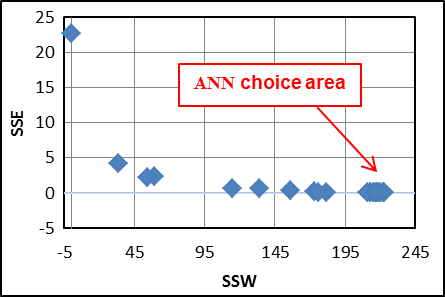 | Figure 6. SSE and SSW convergence |
|
|
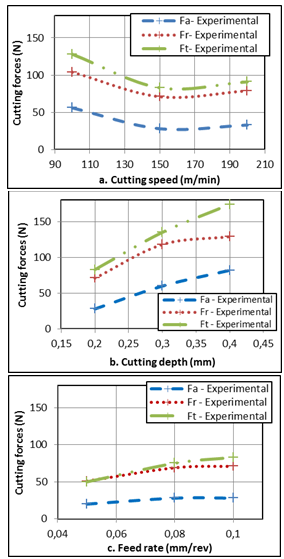
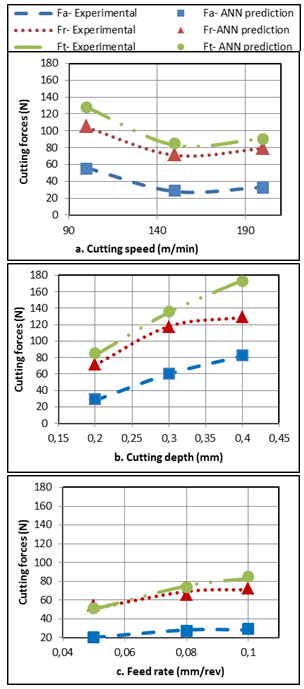 | Figure 7. Experimental and predicted cutting force components as functions of: a.Cutting speed Vc (f =0.1 mm/rev; ap =0.2 mm, 45HRc) b.Cutting depth ap (Vc=150 m/min; f=0,1 mm/rev; 45HRc) c.Feed rate f (Vc=150 m/min; ap=0,2 mm; 45HRc) |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
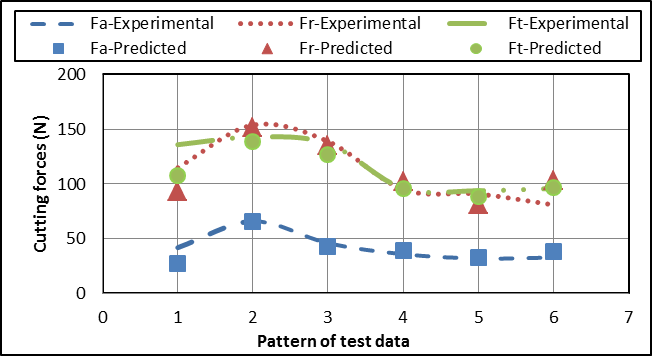 | Figure 8. Experimental and predicted cutting force components in testing for the 4-11-3 structure |
4. Conclusions and Perspectives
- The main objective of this study has been to develop a robust numerical model to predict cutting force components in AISI 52100 bearing steel hard turning using CBN cutting tools using an ANN approach.A precise study has been led to select the more suitable algorithm and methodology:● The number of hidden layers has been tested. Neither using double hidden layer has shown advantage over single hidden layer.● The type of transfer functions in hidden and output layers has been investigated. A sigmoid activation function has been chosen in hidden layer and a linear one in output layer.● Levenberg–Marquardt (LM) algorithm has been compared to Levenberg–Marquardt using Bayesian Regularization (BR/LM). It has appeared that using Bayesian Regularization permits to avoid overfitting in training, which gives thus a major advantage over simple LM algorithm.● And finally, a various number of neurons in hidden layer have been tested, from 1 to 35. It has been noticed first that the algorithm converges when this number reaches 11, and second that a minor overfitting appears when the number of neurons exceeded 13.For the selected 4-11-3 ANN structure, which uses BR/LM algorithm, S.L. activation functions and a single hidden layer, an excellent agreement has been found between numerical predictions and experimental data for the 32 cutting conditions used in training (average MAPE under 2%). And a quite large discrepancy has been noted on the 6 tested cutting conditions: MAPE ranges from 0 to 36% on the 18 cutting force components dataset. Globally, the developed ANN model remains nevertheless efficient and as accurate as what is found in literature and should be recommended in machining process modeling.As a perspective, it seems essential to expand this approach. It could be first possible to compare the proposed numerical approach with analytical models, and then propose hybrid methods based on an analytical approach combined with numerical technics. Moreover, some major ANN parameters such as learning rate and momentum term need to be investigated in order to reinforce the model accuracy. Finally, some other algorithms such as SCG could provide some improvements to the ANN model too.
References
| [1] | Dimla, D. E., Application of perceptron neural networks to tool state classification in metal-turning operation. Elsevier, Engineering Applications of Artificial Intelligence, 12, 471–477, 1999. |
| [2] | Liu, T. L., Chen, W. Y., Anantharaman, K. S., Intelligent detection of drill wear, Elsevier, Mechanical Systems and Signal Processing, 12, 863–873, 1998. |
| [3] | Ezugwua, E. O., Fadarea, D. A., Bonneya, J., Da Silvaa, R. B., Salesa, W. F., Modelling the correlation between cutting and process parameters in highspeed machining of Inconel 718 alloy using an artificial neural network, Elsevier,International Journal of Machine Tools and Manufacture, 45, 1375–1385, 2005. |
| [4] | Oxley, P. L. B., Modelling machining processes with a view to their optimization and to the adaptive control of metal cutting machine tools, Elsevier, Robotics and Computer - Integrated Manufacturing, 4, 103-119, 1988. |
| [5] | Budak, E., Ozlu, E., Development of a thermomechanical cutting process model for machining process simulations, CIRP Annals-Manufacturing Technology, 57, 97-100, 2008. |
| [6] | Szecsi, T., Cutting force modeling using artificial neural networks, Elsevier, Journal of Materials Processing Technology, 92-93, 344- 349, 1999. |
| [7] | Zuperl, U., Cus, F., Tool cutting force modeling in ball-end milling using multilevel perceptron, Elsevier, Journal of Materials Processing Technology, 153–154, 268–275,2004. |
| [8] | Hao, W., Zhu, X., Li, X., Turyagyenda, G., Prediction of cutting force for self-propelled rotary tool using artificial neural networks, Elsevier, Journal of Materials Processing Technology, 180, 23–29, 2006. |
| [9] | Aykut, S., Gölcü, M., Semiz, S., Ergür, H. S., Modeling of cutting forces as function of cutting parameters for face milling of satellite 6 using an artificial neural network, Elsevier, Journal of Materials Processing Technology, 190, 199–203, 2007. |
| [10] | Li, X. P., Iynkaran, K., Nee, A. Y. C., A hybrid machining simulator based on predictive machining theory and neural network modeling, Elsever, Journal of Material Processing Technology, 89-90, 224–230, 1999. |
| [11] | Özel, T., Karpat, K., Predictive modeling of surface roughness and tools wear in hard turning regression and neural networks, Elsevier, International Journal of Machine Tools and Manufacture, 45, 467-479, 2005. |
| [12] | Umbrello, D., Ambrogio, G., Filice, L.,Shivpuri, R., An ANN approach for predicting subsurface residual stresses and the desired cutting conditions during hard turning, Elsevier, Journal of Materials Processing Technology, 189, 143–152, 2007. |
| [13] | Umbrello, D., Ambrogio, G., Filice, L., Shivpuri, R., A hybrid finite element method–artificial neural network approach for predicting residual stresses and the optimal cutting conditions during hard turning of AISI 52100 bearing steel,Elsevier, Materials & Design, Advances in production and processing of aluminum, 29, 873–883, 2008. |
| [14] | Habak, M., Etude de l'influence de la microstructure et des paramètres de coupe sur le comportement en tournage dur de l'acier à roulement 100Cr6, Ph.D. Thesis ENSAM, CER d'Angers, France, 2006. |
| [15] | Maunayri, H., Novel Artificial Neural Networks Force Model for end Milling, Springer, International Journal of Advanced Manufacturing Technology, 18, 693-700, 2001. |
| [16] | Haykin, S., Neural Networks : A Comprehensive Foundation, New York, Macmillan, 1994. |
| [17] | Asiltürk, I., Çunkaș, M., Modeling and prediction of surface roughness in turning operations using artificial neural network and multiple regression method,Elsevier, Expert Systems with Applications, 38, 5826-5832, 2010. |
| [18] | Correa, M., Bielza, C., Pamies-Teixeira, J., Comparison of Bayesian networks and artificial neural networks for quality detection in a machining process, Elsevier, Expert systems with Applications, 36, 7270-7279, 2009. |
| [19] | Özel, T., Nadgir, A., Prediction of flank wear by using back propagation neural network modeling when cutting hardened H-13 steel with chamfered and honed CBN tools. Elsevier, International Journal of Machine Tools and Manufacture. 42, 287-297, 2002 |
| [20] | Reed, R. D., Neural smithing. MIT Press, Cambridge, 1999. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML