E. A. Gomaa 1, B. A. M. Al-Jahdali 2
1Chemistry Department, Faculty of Science Mansoura University, Egypt
2Chemistry Department, Faculty of Applied Science, Umm Al-Qura, Makkah Saudi Arabia
Correspondence to: E. A. Gomaa , Chemistry Department, Faculty of Science Mansoura University, Egypt.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The interaction between Cd2+ ion and Kryptofix 22 in pure MeOH and DMF solvents and their binary mixtures (0-100 % MeOH-DMF) at different temperatures (298.15-313.15) were measured by conductometric titrations. The conductance data in all cases were analysed using the Fuoss - Shedlovsky and Fuoss-Kraus methods to get the limiting molar conductance (Λ0 and the association constant (KA) simultaneously. Accordingly, the computer program of Fuoss equation has been used. The conductance studies indicate the formation of 1:1 complex between the Cd2+ ion and Kryptofix 22. From the conductivity data obtained, the values of the Walden products (Λoηo) were also calculated. Based on the composition dependence of Walden products, the influence of the solvent composition on the solvation of the ion has been discussed. Thermodynamic parameters as well as refractive indices have been determined for Cd2+ ion in the mixed solvents at different temperatures with respect to solute-solvent interaction. This work gives a lot of data for cadmium ions which help in analysis.
Keywords:
Conductance, Cadmium Ion, Salvation, Association, Kryptofix-22, Thermodynamics of Solvation
1. Introduction
Macrocyclic polyether’s were used recently for many applications on both scientific and applied fields in chemistry. The main goal of the present investigation is to study the interaction of some divalent metal ions i.e., Cd(NO3)2, with Kryptofix 22 in mixed solvent of methanol (MeOH) and dimethylformamide (DMF) at four temperatures (298.15, 303.15, 308.15 and 313.15 k). The interaction was studied electrochemically by the use of conductivity measurements. A lot of data on the association, dissociation and thermodynamic parameters of Cd(NO3)2 with Cryptand in MeOH–DMF mixtures were determined in order to facilitate the research for biologist in selecting the necessary ligand for getting rid of toxic salts found in the environment. Macrocyclic crown ethers have some applications in biological activity, industrial production, corrosion chemistry and phase transfer catalysts.In complexation process, macrocycle ligands compete with solvent molecules towards the metal cations in solution. As a result, variation of the solvent can produce a significant change in the apparent binding properties of these ligands. Specifically, solvents of low dielectric constants andsolvating power lead to the greater complex stability than those tend to strong solvation of the metal cations. In addition, the selectivity for certain cations over others may be altered according to the reaction medium[1].The experimental values of refractive indices for Cd(NO3)2 in mixed solvents, the excess refractive indices were calculated and their values show maximum solute–solvent interaction at about 80% MeOH percentage in the mixtures. Also, the electrical conductance data the association, dissociation and thermodynamic parameters for Cd(NO3)2 in presence and absence of Cryptand in mixed solvents (MeOH-DMF) at the above mentioned temperatures are calculated. The association and dissociation parameters are evaluated by using Fuoss-Shedlovsky method and their values are also supported with Fuoss-Kraus method. The computer program of Fuoss equation has been used. It was concluded that the association parameters for the salt used with Cryptand are generally increased by increasing the percentage of methanol in the mixed solvents.
2. Experimental
Methanol (MeOH, 99.8%), dimethylformamide (DMF, BDH, 99.8%) were used without further purification. The purity of the solvents was ascertained by comparing experimental values of densities and viscosities with those reported in the literature. Binary mixtures were prepared by mixing known volumes of each liquid in a stopper glass bottle where the percentage by volume of the organic solvents varied from 0% to 100%. Both of the solvents were stored in sealed containers to prevent contamination with carbon dioxide and water from the air. Cadmium nitrate (Cd(NO3)2, 99%), was provided from BDH. The salt was dried first in an oven at 100 °C and then stored in a desiccators over silica gel for at least 24 h. The kryptofix 22 used was provided from Fluka and used as received without any further purification. The structure of the Kryptofix 22 is given below.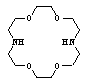 | Stucture of Kryptofix 22 1,7,10,16-Tetraoxa-4,13-diazacyclooctadecane, C12H26N2O4; M. Wt. 262.35 |
The viscosity (η) of the pure solvents and binary mixtures over the entire range of composition and at the desired temperatures were measured using a calibrated U-type Ostwald viscometers immersed in a transparent glass-walled water bath having a thermal stability of ±0.02K. Then the absolute viscosity (η) was calculated by the following equation: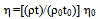 | (1) |
Where ρ1ρ0, t1t0 and η1η0 refer to the density, flow time, and viscosity of pure solvents or binary mixtures and water respectively (Table 1). The refractive indices (nd) of pure solvents, binary mixtures and salt solutions at the desired temperatures were measured by an Abbe refractometer which was connected with ultra thermostat of the type (mgw Lauda cs-20) with accuracy to ± 0.01℃. The dielectric constants (ε) of the pure solvents at different temperatures were taken by interpolation from the data in the literature[1] , and dielectric constant for any solvent mixtures at the desired temperatures were calculated from the following equation: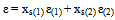 | (2) |
Where xs(1) and xs(2) are the mole fraction by weight of the first and the second organic solvents, respectively; ε(1) and ε(2) are the dielectric constants of first and the second organic solvents in the binary organic-organic mixtures respectively. The results are shown in Table (2).Conductance measurements were carried out with a standard digital direct reading conductivity meter of the type Jenway 4310 and a conductivity cell of cell constant 0.6 cm−1. Also, some measurements were performed using a Beckman conductivity bridge model RE-18A in which the resistance of solution was determined in a jacketed glass cell permitting circulation of water in the jacket after connecting the cell with ultra thermostat of the type (mgw Luda S-20) and kept in a thermostat maintained at the desired temperature ±0.01℃ for approximately 20 min, and then its specific conductivity or resistance was noted .These conductivity data is accurate and technical very good , easy and novel method for cadmium ion determination.
3. Results and Discussion
The effects of Cd(NO3)2 concentrations on the molar conductance (Λ) in the absence and presence of Kryptofix 22 were extensively studied. Straight lines were obtained in the concentration range used at the different temperatures 298.15, 303.15, 308.15 and 313.15 K. The limiting molar conductance (Λ0) was obtained from the extrapolating the linear Onsager plots (Λ) versus (C1/2) of Cd(NO3)2 to zero concentration[2] . The association constant (KA) could be calculated by using two different methods of calculations, involving analysis of the experimental conductivity data (Λ) and (Λ0) by using computer program. The two methods are:
3.1. Fuoss - Shedlovsky Method
In this method the values of association constant (KA) were calculated by using the sets of the following equations from (3) to (10)[2-5] :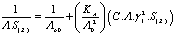 | (3) |
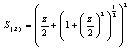 | (4) |
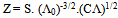 | (5) |
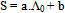 | (6) |
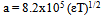 | (7) |
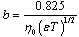 | (8) |
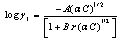 | (9) |
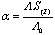 | (10) |
KA is the association constant, (C) is the concentration of metal cation at the chosen points in the relation between (Λ) and, (γ±) is the mean activity coefficients estimated from the Debye Hückel limiting law as modified by Robinson and Stockes, (ε) is the dielectric of the solvents,(η0) is the viscosity of the solvents, (S) is the Onsager coefficient and finally (α) is the degree of dissociation(6, 7) (Tables 5-8). The physical parameters like dielectric constant (ε) and viscosity (η0) and refractive indices (nd) for pure solvents and their mixtures at different temperatures which used in the analysis of the conductance data were taken from Tables (1)-(3).
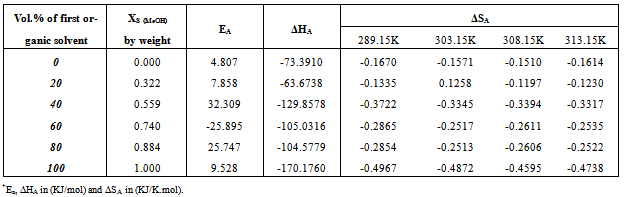
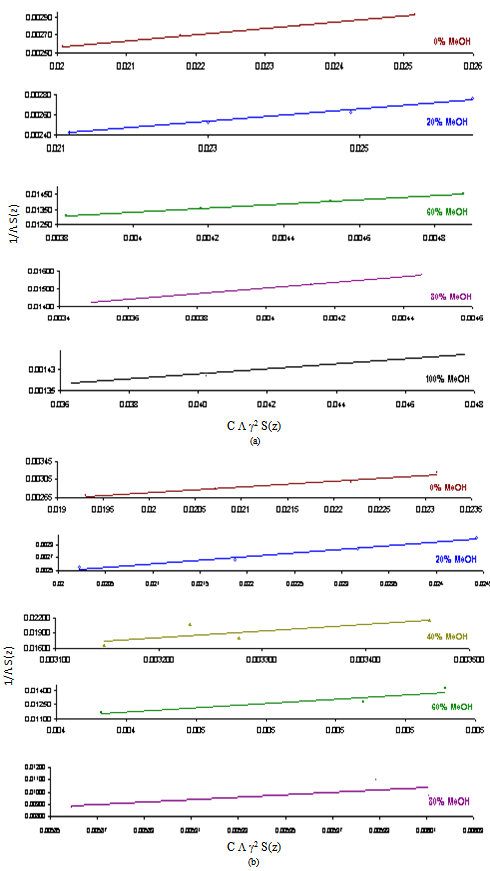
3.2. Fuoss-Kraus Method
In this method the values of association constant (KA) were recalculated by applying Fuoss-Kraus method[5] of calculation depending on Eq.5. The purpose was achieved by plotting the relation of (1/Λ°.S(Z))vs.(CΛ γ±2S(Z)) which gave in all cases straight lines. Figures 1-2 represent the plots of (1/Λ0.S(Z))vs.(CΛ γ±2S(Z)) from the Fuoss-Kraus method for some metal complexes in all mixed solvents and at different temperatures.Good agreement between the two above methods in association parameters is observed and the comparable results were tabulated in table (4). The conductance studies indicate 1:1 complex formation between the Cd2+ ion and Kryptofix. In most cases the association parameters of Cd2+ in absence and presence of Cryptand are greater in mixed solvents than in methanol. This is mainly due to the hydrogen bond strength in pure methanol which decreases in the mixed solvents and therefore facilitates the association of the cation. It is concluded that the association constants generally increase by increasing the percentage of methanol in the mixed solvents (MeOH-DMF) due to the increase of association and decrease in the dissociation degree (α),dissociation constants (KD) and the decrease in ion–ion interaction (activity coefficients γ) on the presence of different Cryptand compounds. The degree of dissociation is almost constant in absence of Cryptand but a very large change (decreased) is observed on adding Cryptands to enhance and increase the association. The values of dissociation constant (KD), the triple ion association constant (K3)[2,6,7] were calculated and recorded in tables (5-12).The Walden product values [2, 8] (Λoηo) were calculated for Cd(NO3)2 in mixed mixtures of MeOH-DMF. The Walden product values as calculated from the limiting molar conductance values (Λ°) were informative from the point of view for ion-solvent interactions. The fluidity ratios (RX) were also calculated and their values are given in Tables (5-12). It was observed that RX values were increased in the mixed solvents than in the pure MeOH or DMF solvents, this was an indication of selective salvation of the electrolyte. The decrease in the products of Λoηo indicates a strong solvent-solute interaction. As a result of that the solvent decrease the mobility of the ions. Activation Energies (EA), Association Enthalpies (ΔHA) and Association Entropies (TΔSA) of Cd(NO3)2 solutions mixed (MeOH-DMF) were calculated, on plotting (log Λ0) values versus 1/T for Cd(NO3)2 in absence and presence of Cryptands straight lines were obtained. From their slopes[9] the Ea were evaluated and represented in Tables (13-14). It was observed that the Ea values for Cd(NO3)2 in presence of Cryptand were greater than that in absence of CryptandActivation energies values are greater in the mixed solvents than that of pure solvents due to mainly to solvent-solvent interactions. The values of Gibbs free energies of association (ΔGA) of Cd(NO3)2 in mixed MeOH-DMF solvents were calculated from the association constant values by using Eq. 11.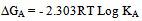 | (11) |
From the calculated ΔGA values, the free energy of transfer (ΔGt) from methanol (M) to the mixed MeOH-DMF (s) solvents was calculated. The values of ΔGA and ΔGt are also, reported in Tables (5-12) and in Figures (3-4). From the plots of logarithmic association constant values (Log KA) of Cd(NO3)2 in absence and presence of Kryptofix 22 against the reciprocal values of the four temperatures 298.15, 303.15, 308.15 and 313.15K at the 1:1 (L:M)[10-12] ligand-metal ratio, straight lines were observed. From there straight relations shown in Figs. 3-4 the association enthalpies were calculated from their slopes (slope = ΔHA/2.303RT). The calculated ΔHA values are tabulated in Tables (13-14). The entropies of association (TΔSA) of Cd(NO3)2 were calculated by the use of Gibbs-Helmholtz equation: 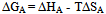 | (12) |
The calculated ΔSA values are tabulated also in Tables (13-14). It is observed from these tables that the ΔHA and ΔSA values are increased with the increase of MeOH contents in the mixtures, which favour more association in the presence of methanol than in MeOH-DMF mixtures. Also, the enthalpies and entropies of Cd(NO3)2 association were increased by also adding Cryptand.This order favours more association. From the thermodynamic parameters calculated, it was found that all these parameters are increased by increasing temperatures. This is due to the increase of interaction between Cd2+ and Cryprtand by increasing temperature. The refractive indices of the mixed solvents (MeOH-DMF) and salt solutions ofCd(NO3)2 in mixed solvents at different temperatures (298.15, 303.15, 308.15 and 313.15K) were measured. And from the refractive indices (nd) values, the excess refractive indices (nd(E)) were calculated by applying eq.(13)[5-7,10-12]: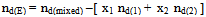 | (13) |
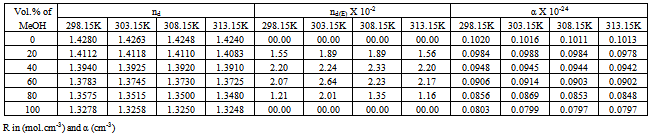
Where (x1) and (x2) are the mole fraction of solvent 1 (MeOH) and solvent 2 (DMF) in their mixtures, (nd) is the measured refractive indices of the mixed solvents or the salt solution. The values of (nd) and (nd(E)) of MeOH-DMF mixtures and the metal are given in Table (3). The excess refractive indices show maximum values at 80% MeOH-DMF percentages at all the used temperatures indicating maximum solute-solvent interactions at this percentage (Figure 5-6).Table 1. The viscosities* (η0) of MeOH-DMF mixtures at 298.15, 303.15, 308.15 and 313.15 K
 |
| |
|
| Table 2. The dielectric constants (ε) of MeOH-DMF mixtures at 298.15, 303.15, 308.15 and 313.15 K |
| | Vol.% of MeOH | XMeOH | MeOH-DMF | | 298.15 K | 303.15 K | 308.15 K | 313.15 K | | 0 | 0.0000 | 38.6000 | 37.6000 | 36.2000 | 34.7000 | | 20 | 0.3222 | 36.6990 | 35.7320 | 34.3641 | 32.9013 | | 40 | 0.559 | 35.3019 | 34.3586 | 33.0143 | 31.5758 | | 60 | 0.7404 | 34.2316 | 33.3063 | 31.9802 | 30.5588 | | 80 | 0.8838 | 33.3856 | 32.4743 | 31.1626 | 29.7535 | | 100 | 1.0000 | 32.7000 | 31.8000 | 30.5000 | 29.1000 |
|
|
Table 3. The refractive indices (nd), the excess refractive indices (nd(E)) and the molecular dipole polarizability* (α) of Cd(NO3)2 in MeOH-DMF mixtures at 298.15, 303.15, 308.15 and 313.15 K
 |
| |
|
| Table 4. Fuoss-Kraus association constant[Log KA (F-K)] in comparison with Fuoss-Shedlovsky data[Log KA (F-Sh)] for Cd(NO3)2 in presence of Kry-22 in mixed MeOH-DMF mixtures at 298.15, 303.15, 308.15 and 313.15K |
| | Vol% of MeOH | 298.15 K | 303.15 K | 308.15 | 313.15 K | | Log KA(F-K) | Log KA(F-Sh) | Log KA(F-K) | Log KA(F-Sh) | Log KA(F-K) | Log KA(F-Sh) | Log KA(F-K) | Log KA(F-Sh) | | 0 % | 3.170 | 4.14 | 3.203 | 4.44 | 4.71 | 4.56 | 3.17 | 3.82 | | 20% | 4.71 | 4.18 | 6.09 | 4.41 | 3.42 | 4.55 | 3.47 | 4.20 | | 40% | 4.17 | 3.32 | 4.34 | 4.91 | 6.06 | 4.29 | 5.67 | 4.35 | | 60% | 4.37 | 3.44 | 4.05 | 4.96 | 5.43 | 4.18 | 6.22 | 4.29 | | 80% | 4.35 | 3.42 | 3.60 | 4.90 | 5.01 | 4.12 | 7.09 | 4.28 | | 100% | 3.69 | 3.88 | 3.66 | 3.89 | 3.30 | 4.86 | 3.78 | 3.65 |
|
|
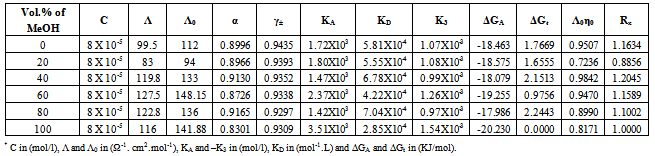
Table 5. The values of molar conductance* (Λ), limiting molar conductance*(Λ0), degree of dissociation (α), activity coefficient (γ±),association constant* (KA), dissociation constant* (KD),triple ion association constant* (-K3),Gibbs free energy of association* (ΔGA), transfer Gibbs free energy of association* (ΔGt), Walden product (Λ0η0) and the fluidity ratio (Rx) of Cd(NO3)2 in MeOH-DMF mixtures at 298.15K
 |
| |
|
Table 6. The values of molar conductance* (Λ), limiting molar conductance*(Λ0), degree of dissociation (α), activity coefficient (γ±),association constant* (KA), dissociation constant* (KD),triple ion association constant* (-K3),Gibbs free energy of association* (ΔGA), transfer Gibbs free energy of association* (ΔGt), Walden product (Λ0η0) and the fluidity ratio (Rx) of Cd(NO3)2 in MeOH-DMF mixtures at 303.15K
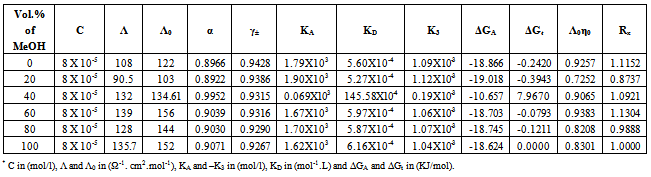 |
| |
|
Table 7. The values of molar conductance* (Λ), limiting molar conductance*(Λ0), degree of dissociation (α), activity coefficient (γ±),association constant* (KA), dissociation constant* (KD),triple ion association constant* (-K3),Gibbs free energy of association* (Δ
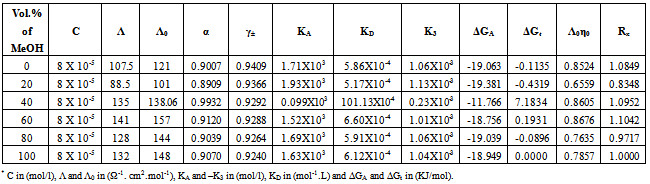 |
| |
|
Table 8. The values of molar conductance* (Λ), limiting molar conductance*(Λ0), degree of dissociation (α), activity coefficient (γ±),association constant* (KA), dissociation constant* (KD),triple ion association constant* (-K3),Gibbs free energy of association* (ΔGA), transfer Gibbs free energy of association* (ΔGt), Walden product (Λ0η0) and the fluidity ratio (Rx) of Cd(NO3)2 in MeOH-DMF mixtures at 313.15K
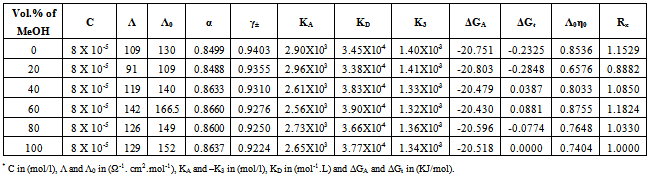 |
| |
|
Table 9. The values of molar conductance* (Λ), limiting molar conductance*(Λ0), degree of dissociation (α), activity coefficient (γ±), association constant* (KA), dissociation constant* (KD),triple ion association constant* (-K3),Gibbs free energy of association* (ΔGA), transfer Gibbs free energy of association* (ΔGA), Walden product (Λ0η0) and the fluidity ratio (Rx) of Cd(NO3)2 in the presence of Kryptofix-22 in MeOH-DMF mixtures at 298.15K
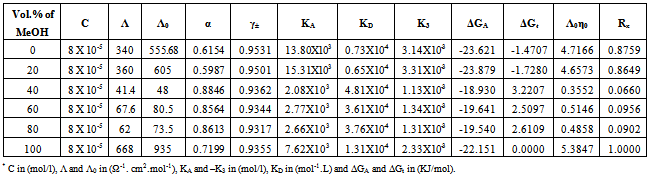 |
| |
|
Table 10. The values of molar conductance* (Λ), limiting molar conductance*(Λ0), degree of dissociation (α), activity coefficient (γ±), association constant* (KA), dissociation constant* (KD),triple ion association constant* (-K3),Gibbs free energy of association* (ΔGA), transfer Gibbs free energy of association* (ΔGA), Walden product (Λ0η0) and the fluidity ratio (Rx) of Cd(NO3)2 in the presence of Kryptofix-22 in MeOH-DMF mixtures at 303.15K
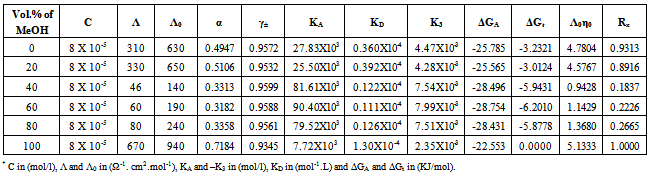 |
| |
|
Table 11. The values of molar conductance* (Λ), limiting molar conductance*(Λ0), degree of dissociation (α), activity coefficient (γ±), association constant* (KA), dissociation constant* (KD),triple ion association constant* (-K3),Gibbs free energy of association* (ΔGA), transfer Gibbs free energy of association* (ΔGA), Walden product (Λ0η0) and the fluidity ratio (Rx) of Cd(NO3)2 in the presence of Kryptofix-22 in MeOH-DMF mixtures at 308.15K
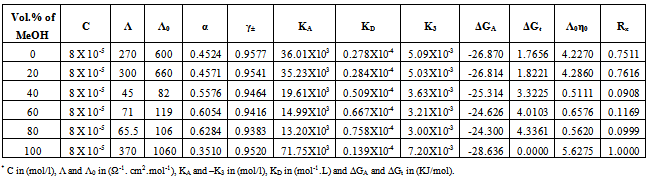 |
| |
|
Table 12. The values of molar conductance* (Λ), limiting molar conductance*(Λ0), degree of dissociation (α), activity coefficient (γ±), association constant* (KA), dissociation constant* (KD),triple ion association constant* (-K3),Gibbs free energy of association* (ΔGA), transfer Gibbs free energy of association* (ΔGA), Walden product (Λ0η0) and the fluidity ratio (Rx) of Cd(NO3)2 in the presence of Kryptofix-22 in MeOH-DMF mixtures at 313.15K
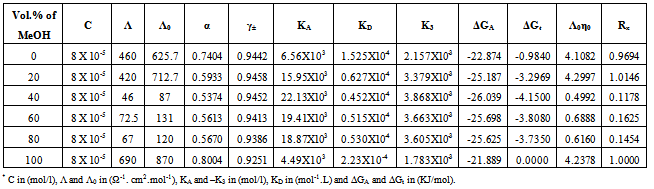 |
| |
|
Table 13. The activation energy* (Ea), the enthalpy* (ΔHA) and the entropy*(ΔSA) changes of association of Cd(NO3)2 in MeOH-DMF mixtures at 298.15, 303.15, 308.15, 313.15K
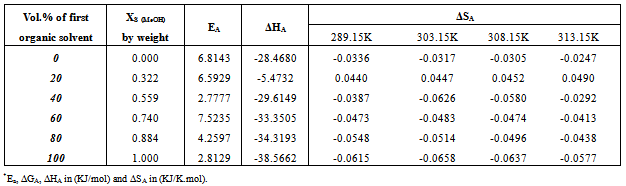 |
| |
|
Table 14. The enthalpy* (ΔHA) and the entropy*(ΔSA) changes of association of Cd(NO3)2 in the presence of Kryptofix-22 in MeOH-DMF mixtures at 298.15, 303.15, 308.15, 313.15K
 |
| |
|
 | Figure 1. Fuoss-Kraus plots of Cd(NO3)2 in presence of Kry-22 in MeOH-DMF mixtures at (a) 298.15K and (b) 303.15K |
 | Figure 2. Fuoss-Kraus plots of Cd(NO3)2 in presence of Kry-22 in MeOH-DMF mixtures at (c) 308.15K and (d) 313.15K |
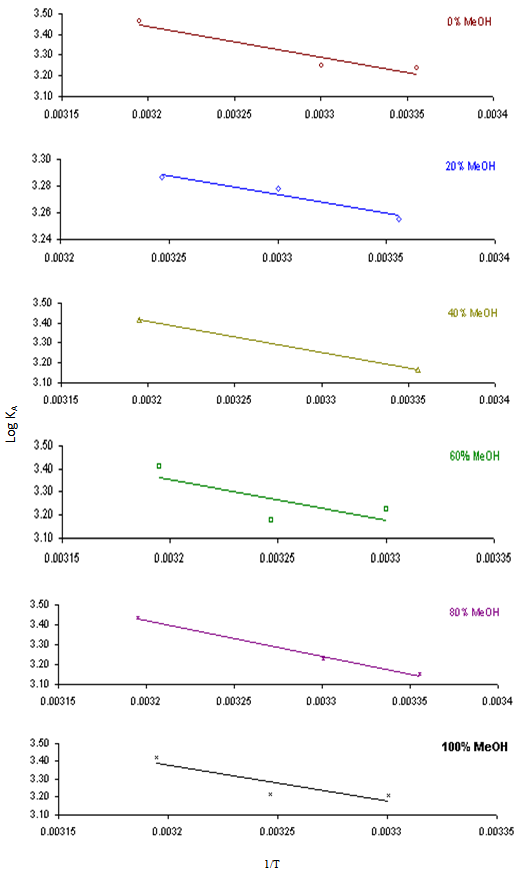 | Figure 3. Variation of Log KA with 1/T in mixed MeOH-DMF solvents for Cd(NO3)2 |
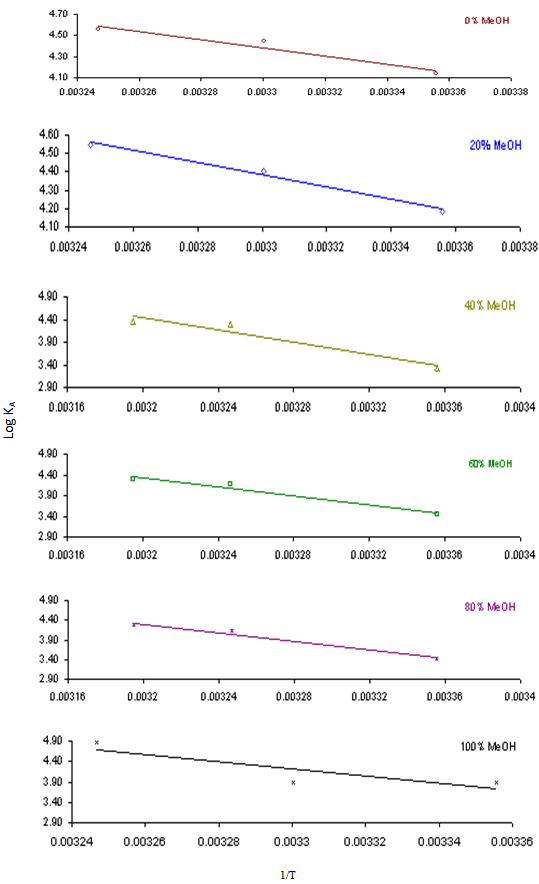 | Figure 4. Variation of Log KA with 1/T in mixed MeOH-DMF solvents for Cd(NO3)2 in presence of Kry-22 |
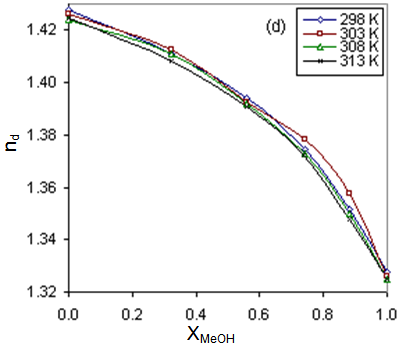 | Figure 5. Variation of the refractive indices (nd) with the mole fraction (XMeOH) by weight of MeOH for Cd(NO3)2 at 298, 303, 308, 313K in mixed MeOH-DMF solvents |
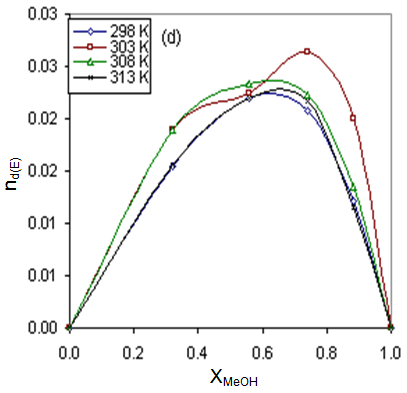 | Figure 6. Variation of the excess refractive indices (nd(E)) with the mole fraction (XMeOH) by weight of MeOH for Cd(NO3)2 at 298, 303, 308, 313K in mixed MeOH-DMF solvents |
References
| [1] | E.A., Gomaa , Thermochimica Acta, 142 (1989) 19 and E. A, Gomaa , , Croatica Chemica Acta, 62 (1989) 475. |
| [2] | E.A.,Gomaa, M.A. ,Hafez, and M.N.H., Moussa, Bull. Soc. Chim. Fr., 3 (1986)361. |
| [3] | E.A.Gomaa, Thermochim. Acta, 99, (1988)128. |
| [4] | M.A., Hafez, E. A. ,Gomaa, and M.N.H., Moussa, First conference of Chem. Faculty of science, Mansoura university, 24-26 Sep. (1986). |
| [5] | A. K., Covington and T.Dickinson,; "Physical Chemistry of Organic Solvent Systems", Plenum Press, London, (1973). |
| [6] | T. Shedlovsky, and R.L Kay, J. Phys., Chem.60(1956)151. |
| [7] | R.M. ,Fuoss, andF., Accascina, Electrolytic conductance, Interscience, New York (1959). |
| [8] | R.A., Robinson, and R, H. ,Stokes ; "Electroyte Solutions", Wiley, P.463 (1968) New York. |
| [9] | P.,Walden; Z.Phys. chem., 78(1912)257. |
| [10] | E. A., Gomaa, Thermochimica. Acta, 152(1989)71. |
| [11] | E. A. Gomaa, Thermochimica. Acta, 156(1989)91. |
| [12] | A.A., EL-Khouly, E.A. ,Gomaa, and S., EL-Ashry, second conf. in Basic science, Assiut University, Assiut 2000. |


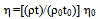
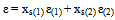
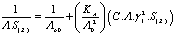
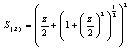
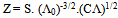
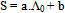
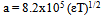
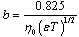
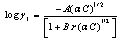
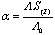
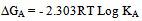
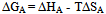
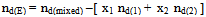






 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML










