Salah H. Abid , Heba A. Hassan
Mathematics department, Education College, Al-Mustansiriya University, Baghdad, Iraq
Correspondence to: Salah H. Abid , Mathematics department, Education College, Al-Mustansiriya University, Baghdad, Iraq.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The Beta Marshall-Olkin extended uniform (BMOEU) distribution is introduced. The rth moment, the mean, the variance, the cumulative distribution function, the reliability function and the hazard rate function is obtained for the new distribution. It is well known that an item fails when a stress to which it is subjected exceeds the corresponding strength. In this sense, strength can be viewed as “resistance to failure”. Good design practice is such that the strength is always greater than the expected stress. The safety factor can be defined in terms of strength and stress as strength/ stress. So, the BMOEU strength-stress model with different eight parameters will be derived here.
Keywords:
Uniform distribution, Marshall-Olkin extended, Stress-strength model
Cite this paper: Salah H. Abid , Heba A. Hassan , The Beta Marshall-Olkin Extended Uniform Distribution, Journal of Safety Engineering, Vol. 4 No. 1, 2015, pp. 1-7. doi: 10.5923/j.safety.20150401.01.
1. Introduction
The continuous uniform distribution represents a situation where all outcomes in a range between a minimum and maximum value are equally likely. From a theoretical perspective, this distribution is a key one in risk analysis; many Monte Carlo software algorithms use a sample from this distribution (between zero and one) to generate random samples from other distributions .Also, there are a real-life processes that have this form of uncertainty. These could include for example: the position of a particular air molecule in a room, the point on a car tyre where the next puncture will occur, the number of seconds past the minute that the current time is, or the length of time that one may have to wait for a train. In oil exploration, the position of the oil-water contact in a potential prospect is also often considered to be uniformly continuously distributed.In statistics, when a p-value is used as a test statistic for a simple null hypothesis, and the distribution of the test statistic is continuous, then the p-value is uniformly distributed between 0 and 1 if the null hypothesis is true.Actually, there are a lot of uses for uniform distribution. Despite of the importance of what has been stated above, but the form of the distribution restricts its use in many other applications.In this paper, we introduce a generalization of the Extended Marshall Olkin Uniform distribution [1], referred to as the Beta Marshall Olkin Extended Uniform distribution (BMOEU) generated from the logit of a beta random variable. We provide a comprehensive treatment of the mathematical properties of this new distribution. For the new distribution, we derive the probability density function, the cumulative distribution, the reliability function, the hazard rate function, the rth moment function and the stress-strength model.We proposed a distribution here with the hope it will attract wider applicability in other fields. The generalization is motivated by the work of Eugene et al. [7]. Eugene et al. (2002) defined the beta G distribution from a quite arbitrary cumulative distributionfunction (cdf), U(x) by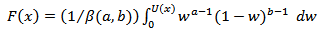 | (1) |
where a >0 and b >0 are two additional parameters whose role is to introduce skewness and to vary tail weight and 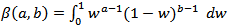 is the beta function. The class of distributions (1) has an increased attention after the works by Eugene et al. (2002) and Jones (2004) [11]. Application of
is the beta function. The class of distributions (1) has an increased attention after the works by Eugene et al. (2002) and Jones (2004) [11]. Application of 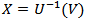 to the random variable V following a beta distribution with parameters a and b, V ∼B(a, b) say, yields X with cdf (1). Eugene et al. (2002) defined the beta normal (BN) distribution by taking U(x) to be the cdf of the normal distribution and derived some of its first moments. General expressions for the moments of the BN distribution were derived (Gupta and Nadarajah, 2004) [9]. Nadarajah and Kotz (2004) [14] also introduced the beta Gumbel (BG) distribution by taking U(x) to be the cdf of the Gumbel distribution and provided closed-form expressions for the moments, the asymptotic distribution of the extreme order statistics and discussed the maximum likelihood estimation procedure. Nadarajah and Gupta (2004) [13] introduced the beta Frechet (BF) distribution by taking U(x) to be the Frechet distribution, derived the analytical shapes of the probability density function (pdf) and the hazard rate function and calculated the asymptotic distribution of the extreme order statistics. However, they do not investigate expressions for its moments and the information matrix which we do in this paper. Also, Nadarajah and Kotz (2005) [15] worked with the beta exponential (BE) distribution and obtained the moment generating function, the first four cumulants, the asymptotic distribution of the extreme order statistics and discussed the maximum likelihood estimation. Barreto-Souza, Santos and Cordeiro (2010).[4] introduced the beta generalized exponential distribution (BGE) that includes the beta exponential and generalized exponential distributions as special cases. They provide a comprehensive mathematical treatment of this distribution. They derived the moment generating function and the rth moment thus generalizing some results in the literature. Expressions for the density, moment generating function and rth moment of the order statistics also are obtained also by them. They discussed estimation of the parameters by maximum likelihood and provide the information matrix. They observed in one application to real data set that this model is quite flexible and can be used quite effectively in analyzing positive data in place of the beta exponential and generalized exponential distributions. Amusan (2010) [2] defined and studied a three-parameter beta Maxwell distribution (BM). Various properties of the distribution were also discussed. The method of maximum likelihood was proposed to estimate the parameters of the distribution. Barreto-Souza, Cordeiro and Simas (2011) [3] derived some mathematical properties of the BF distribution in terms of the corresponding properties of the Frechet distribution. They derived also explicit expansions for the ordinary moments and L-moments and obtain the order statistics and their moments. They discussed also maximum likelihood estimation and calculate the information matrix which was not known. The information matrix is easily numerically determined. Two applications to real data sets are given by them to illustrate the potentiality of this distribution. Cordeiro and Lemonte (2011) [6] proposed the beta-half-Cauchy distribution (BHC) for modeling lifetime data. Various explicit expressions for its moments, generating and quantile functions, mean deviations, and density function of the order statistics and their moments are provided. The parameters of the new model are estimated by maximum likelihood, and the observed information matrix is derived. An application to lifetime real data shows that it can yield a better fit than three- and two-parameter Birnbaum-Saunders, gamma, and Weibull models. Zea, Silva, Bourguignon, Santos and Cordeiro (2012) [17] introduced the beta exponentiated Pareto distribution (BEP). Its density and failure rate functions can have different shapes. It contains as special models several important distributions discussed in the literature, such as the beta-Pareto and exponentiated Pareto distributions. They provided a comprehensive mathematical treatment of the distribution and derived expressions for the moments, generating and quantile functions and incomplete and L-moments. An explicit expression for Renyientropy is obtained. The method of maximum likelihood is used for estimating the model parameters and the observed information matrix is derived. The flexibility of the new model is illustrated with an application to a real data set. Castellares, Montenegro and Cordeiro (2013) [5] introduced the beta log-normal distribution (BLO) for which the log-normal distribution is a special case. Various properties of the new distribution are discussed by them. Expansions for the cumulative distribution and density functions that do not involve complicated functions are derived. They obtained expressions for its moments and for the moments of order statistics. The estimation of parameters is approached by the method of maximum likelihood and the expected information matrix is derived. The new model is quite flexible in analyzing positive data as an important alternative to the gamma, Weibull, generalized exponential, beta exponential and Birnbaum-Saunders distributions. The flexibility of the new distribution is illustrated in an application to a real data set. Rajab, Aleem, Nawaz and Daniyal (2013) [16] developed a new five parameter Beta Lomax Distribution (BLO) from a three parameter Lomax Distribution. They developed expressions for the rth moment; Skewness and Kurtosis of three parameters Lomax, and five parameters Beta Lomax Distribution. At the end, the Maximum Likelihood Estimators (MLE) of the parameters is obtained also. Merovci and Sharma (2014) [12] introduced beta-Lindley distribution that extends the Lindley distribution (BL). They provided a comprehensive mathematical treatment of this distribution. They derived the moment generating function and the rth moment thus, generalizing some results in the literature. Expressions for the density, moment generating function, and rth moment of the order statistics also are obtained. Further, they also discussed estimation of the unknown model parameters in both classical and Bayesian setup. The usefulness of the new model is illustrated by means of two real data sets. Jafari, Tahmasebi and Alizadeh (2014) [10] introduced a new four-parameter generalized version of the Gompertz model which is called Beta-Gompertz (BG) distribution. It includes some well-known lifetime distributions such as Beta-exponential and generalized Gompertz distributions as special sub-models. Some mathematical properties of the new distribution, such as closed-form expressions for the density, cumulative distribution, hazard rate function, the kth order moment, moment generating function, Shannon entropy, and the quantilemeasure are provided. They discussed maximum likelihood estimation of the BG parameters from one observed sample and derive the observed Fisher’s information matrix. A simulation study is performed in order to investigate the properties of the proposed estimator. At the end, in order to show the BG distribution flexibility, an application using a real data set is presented. We can write (1) as,
to the random variable V following a beta distribution with parameters a and b, V ∼B(a, b) say, yields X with cdf (1). Eugene et al. (2002) defined the beta normal (BN) distribution by taking U(x) to be the cdf of the normal distribution and derived some of its first moments. General expressions for the moments of the BN distribution were derived (Gupta and Nadarajah, 2004) [9]. Nadarajah and Kotz (2004) [14] also introduced the beta Gumbel (BG) distribution by taking U(x) to be the cdf of the Gumbel distribution and provided closed-form expressions for the moments, the asymptotic distribution of the extreme order statistics and discussed the maximum likelihood estimation procedure. Nadarajah and Gupta (2004) [13] introduced the beta Frechet (BF) distribution by taking U(x) to be the Frechet distribution, derived the analytical shapes of the probability density function (pdf) and the hazard rate function and calculated the asymptotic distribution of the extreme order statistics. However, they do not investigate expressions for its moments and the information matrix which we do in this paper. Also, Nadarajah and Kotz (2005) [15] worked with the beta exponential (BE) distribution and obtained the moment generating function, the first four cumulants, the asymptotic distribution of the extreme order statistics and discussed the maximum likelihood estimation. Barreto-Souza, Santos and Cordeiro (2010).[4] introduced the beta generalized exponential distribution (BGE) that includes the beta exponential and generalized exponential distributions as special cases. They provide a comprehensive mathematical treatment of this distribution. They derived the moment generating function and the rth moment thus generalizing some results in the literature. Expressions for the density, moment generating function and rth moment of the order statistics also are obtained also by them. They discussed estimation of the parameters by maximum likelihood and provide the information matrix. They observed in one application to real data set that this model is quite flexible and can be used quite effectively in analyzing positive data in place of the beta exponential and generalized exponential distributions. Amusan (2010) [2] defined and studied a three-parameter beta Maxwell distribution (BM). Various properties of the distribution were also discussed. The method of maximum likelihood was proposed to estimate the parameters of the distribution. Barreto-Souza, Cordeiro and Simas (2011) [3] derived some mathematical properties of the BF distribution in terms of the corresponding properties of the Frechet distribution. They derived also explicit expansions for the ordinary moments and L-moments and obtain the order statistics and their moments. They discussed also maximum likelihood estimation and calculate the information matrix which was not known. The information matrix is easily numerically determined. Two applications to real data sets are given by them to illustrate the potentiality of this distribution. Cordeiro and Lemonte (2011) [6] proposed the beta-half-Cauchy distribution (BHC) for modeling lifetime data. Various explicit expressions for its moments, generating and quantile functions, mean deviations, and density function of the order statistics and their moments are provided. The parameters of the new model are estimated by maximum likelihood, and the observed information matrix is derived. An application to lifetime real data shows that it can yield a better fit than three- and two-parameter Birnbaum-Saunders, gamma, and Weibull models. Zea, Silva, Bourguignon, Santos and Cordeiro (2012) [17] introduced the beta exponentiated Pareto distribution (BEP). Its density and failure rate functions can have different shapes. It contains as special models several important distributions discussed in the literature, such as the beta-Pareto and exponentiated Pareto distributions. They provided a comprehensive mathematical treatment of the distribution and derived expressions for the moments, generating and quantile functions and incomplete and L-moments. An explicit expression for Renyientropy is obtained. The method of maximum likelihood is used for estimating the model parameters and the observed information matrix is derived. The flexibility of the new model is illustrated with an application to a real data set. Castellares, Montenegro and Cordeiro (2013) [5] introduced the beta log-normal distribution (BLO) for which the log-normal distribution is a special case. Various properties of the new distribution are discussed by them. Expansions for the cumulative distribution and density functions that do not involve complicated functions are derived. They obtained expressions for its moments and for the moments of order statistics. The estimation of parameters is approached by the method of maximum likelihood and the expected information matrix is derived. The new model is quite flexible in analyzing positive data as an important alternative to the gamma, Weibull, generalized exponential, beta exponential and Birnbaum-Saunders distributions. The flexibility of the new distribution is illustrated in an application to a real data set. Rajab, Aleem, Nawaz and Daniyal (2013) [16] developed a new five parameter Beta Lomax Distribution (BLO) from a three parameter Lomax Distribution. They developed expressions for the rth moment; Skewness and Kurtosis of three parameters Lomax, and five parameters Beta Lomax Distribution. At the end, the Maximum Likelihood Estimators (MLE) of the parameters is obtained also. Merovci and Sharma (2014) [12] introduced beta-Lindley distribution that extends the Lindley distribution (BL). They provided a comprehensive mathematical treatment of this distribution. They derived the moment generating function and the rth moment thus, generalizing some results in the literature. Expressions for the density, moment generating function, and rth moment of the order statistics also are obtained. Further, they also discussed estimation of the unknown model parameters in both classical and Bayesian setup. The usefulness of the new model is illustrated by means of two real data sets. Jafari, Tahmasebi and Alizadeh (2014) [10] introduced a new four-parameter generalized version of the Gompertz model which is called Beta-Gompertz (BG) distribution. It includes some well-known lifetime distributions such as Beta-exponential and generalized Gompertz distributions as special sub-models. Some mathematical properties of the new distribution, such as closed-form expressions for the density, cumulative distribution, hazard rate function, the kth order moment, moment generating function, Shannon entropy, and the quantilemeasure are provided. They discussed maximum likelihood estimation of the BG parameters from one observed sample and derive the observed Fisher’s information matrix. A simulation study is performed in order to investigate the properties of the proposed estimator. At the end, in order to show the BG distribution flexibility, an application using a real data set is presented. We can write (1) as,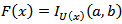 | (2) |
Where, 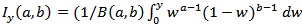 , denotes the incomplete beta function ratio, i.e., the cdf of the beta distribution with parameters a and b. For general a and b, we can express (2) in terms of the well-known hypergeometric function defined by,
, denotes the incomplete beta function ratio, i.e., the cdf of the beta distribution with parameters a and b. For general a and b, we can express (2) in terms of the well-known hypergeometric function defined by, 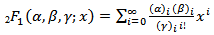 Where
Where 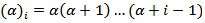 denotes the ascending factorial. We obtain,
denotes the ascending factorial. We obtain,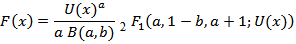 The properties of the cdf, F(x) for any beta U distribution defined from a parent
The properties of the cdf, F(x) for any beta U distribution defined from a parent 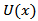 in (1), could, in principle, follow from the properties of the hypergeometric function which are well established in the literature; see, for example, Section 9.1 of Gradshteyn and Ryzhik (2000) [8]. The probability density function (pdf) corresponding to (1) can be written in the form,
in (1), could, in principle, follow from the properties of the hypergeometric function which are well established in the literature; see, for example, Section 9.1 of Gradshteyn and Ryzhik (2000) [8]. The probability density function (pdf) corresponding to (1) can be written in the form,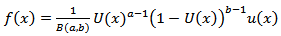 | (3) |
where 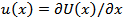 is the pdf of the parent distribution. The pdf
is the pdf of the parent distribution. The pdf 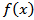 will be mosttractable when the functions
will be mosttractable when the functions 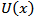 and
and 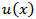 have simple analytic expressions as is the caseof the MOEU distribution. The cdf and pdf of the Marshall Olkin Extended Uniform distribution (MOEU) distribution are, respectively [1],
have simple analytic expressions as is the caseof the MOEU distribution. The cdf and pdf of the Marshall Olkin Extended Uniform distribution (MOEU) distribution are, respectively [1],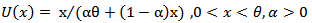 | (4) |
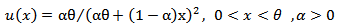 | (5) |
So, the reliability function is,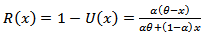 | (6) |
where 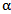 is the shape parameter and
is the shape parameter and 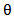 is the scale parameter of the distribution.The hazard rate function of MOEU
is the scale parameter of the distribution.The hazard rate function of MOEU 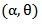 distribution is,
distribution is,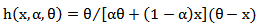 | (7) |
and the rth moment of MOEU 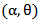 distribution is,
distribution is,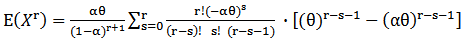 | (8) |
and then the first four essential moments mean, variance, skewness and kurtoses are,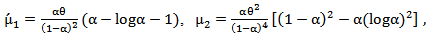
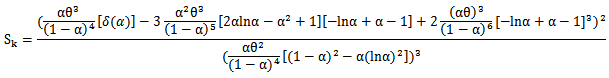 Where,
Where, 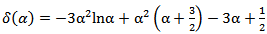 ,
, 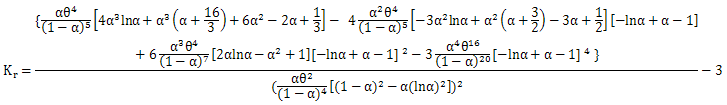 The coefficient of variation is,
The coefficient of variation is, 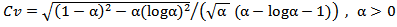 . And it depends only on parameter
. And it depends only on parameter 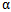 . The q thquantile of a
. The q thquantile of a 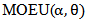 distribution is given by
distribution is given by 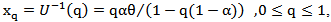 Where
Where 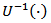 is the inverse distribution function.According to (3) and some of the above properties of a
is the inverse distribution function.According to (3) and some of the above properties of a 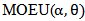 distribution, we get the Beta Marshall Olkin Extended Uniform distribution (BMOEU) with the following pdf,
distribution, we get the Beta Marshall Olkin Extended Uniform distribution (BMOEU) with the following pdf,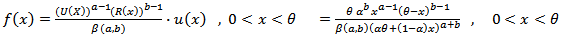 | (9) |
The rth moment of the new 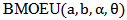 distribution is,
distribution is,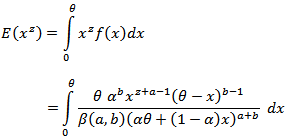 Since,
Since,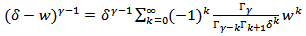 | (10) |
then,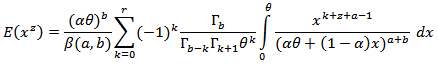 And since,
And since,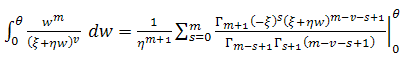 | (11) |
By putting, 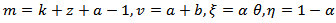 we get,
we get, 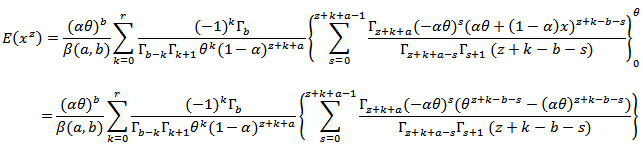 | (12) |
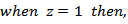 the mean is,
the mean is,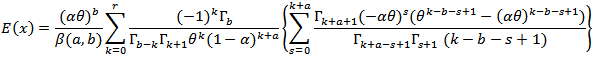 | (13) |
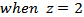 , one can get the variance
, one can get the variance 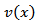 as,
as,
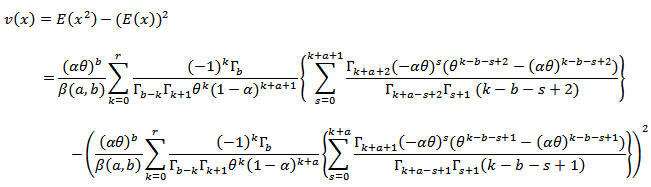 | (14) |
The cumulative distribution function can be derived as follows, 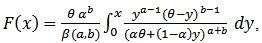
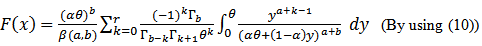 By using (11) with,
By using (11) with, 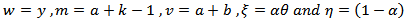 , we get
, we get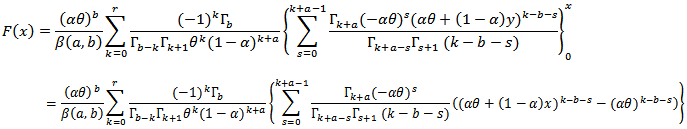 | (15) |
So, the reliability function will be,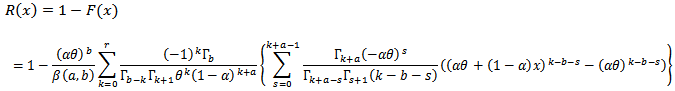 | (16) |
And then the hazard rate is,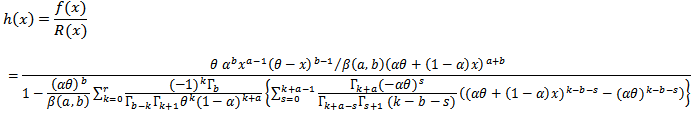 | (17) |
2. Stress Strength Reliability
The Stress–strength analysis is the analysis of the strength of the materials and the interference of the stresses placed on the materials, where "materials" is not necessarily the raw goods or parts, but can be an entire system. Stress-Strength Analysis is a tool used in reliability engineering. Stress-strength analysis has been used in mechanical component design. Inferences about R = P[Y < X], where X and Y are two independent random variables, is very common in the reliability literature. For example, if X is the strength of a component which is subject to a stress Y, then R is a measure of system performance and arises in the context of mechanical reliability of a system. The system fails if and only if at any time the applied stress is greater than its strength.So, following we will derived the BMOEU strength-stress model with different eight parameters.Let x and y be the strength and stress random variables, independent of each other, follow respectively 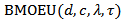 and
and 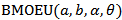 , then, the stress-strength reliability model is,
, then, the stress-strength reliability model is,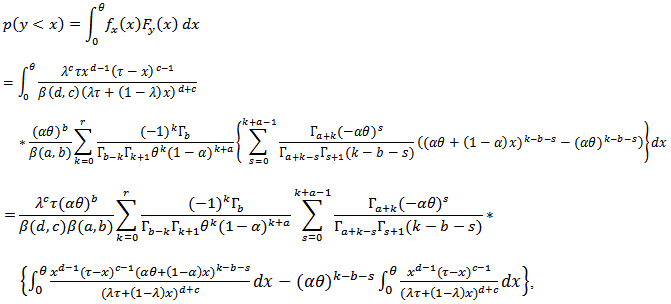 Below, we'll solve integrals inside the brackets above each one separately, so the solution of the first integral is,
Below, we'll solve integrals inside the brackets above each one separately, so the solution of the first integral is,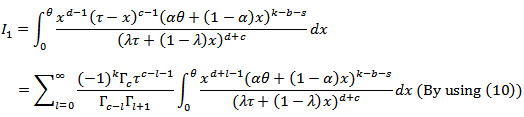 Since,
Since,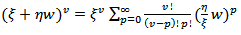 | (18) |
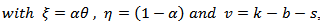 we get,
we get, 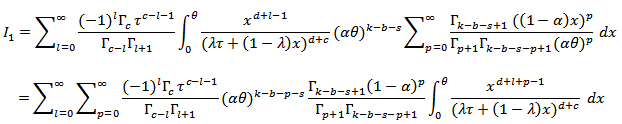 Since,
Since, 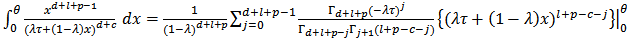 by using (11) with
by using (11) with 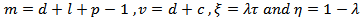 we get,
we get,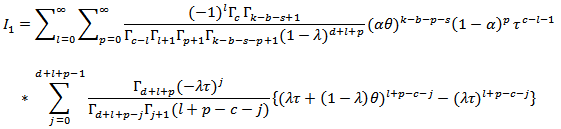 The solution of the second integral is,
The solution of the second integral is,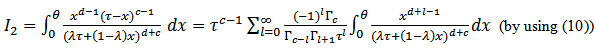 By using (11) with,
By using (11) with, 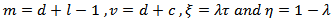 , we get,
, we get,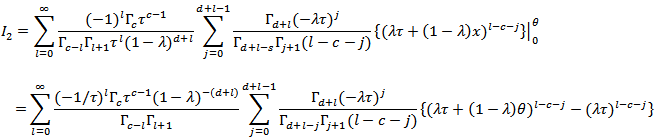 Finally the stress-strength reliability is
Finally the stress-strength reliability is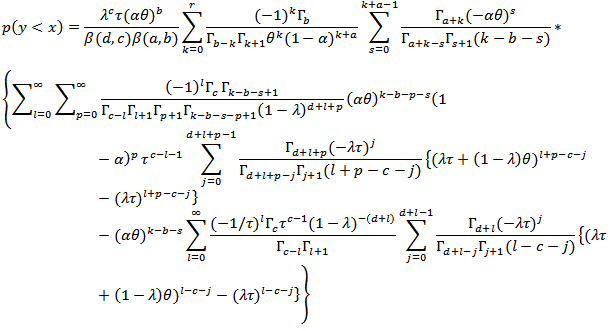 | (19) |
3. Summary and Conclusions
In spite of the great importance of the uniform distribution uses, but unfortunately the form of the distribution and its properties reduced the distribution applications, especially in real life. This issue has made us think to construct other distributions based on the uniform distribution, So that the new distributions have flexible forms and properties to represent a lot of other applications.The Beta Marshall-Olkin extended uniform (BMOEU) distribution is introduced. Some important distributional properties is obtained for the new distribution, alongside the BMOEU strength-stress model with different eight parameters will be derived here.
References
| [1] | Abid, Salah H. and Hassan, Heba A. (2014) "The Marshall-Olkin extended Uniform stress-strength model", American Journal of Math. and Stat. ,Volume 4, Number 6, December. |
| [2] | Amusan, G. (2010) "The Beta Maxwell Distribution" , Master thesis of mathematics, Graduate College of Marshall University. |
| [3] | Barreto-Souza, W. & Cordeiro, G. and Simas, A. (2011) "Some Results for Beta Fréchet Distribution"; Comm. in Stat. - Theory and Methods, Volume 40, Issue 5, 798-811. |
| [4] | Barreto-Souza, W. & Santos, A. and & Cordeiro, G. (2010) "The beta generalized exponential distribution" Volume 80, Issue 2, p.159-172. |
| [5] | Castellares, F. & Montenegro, L. and Cordeiro, G. (2013) "The Beta Log-normal Distribution", Journal of Stat.Compu. and Simulation, Volume 83, Issue 2, p.203-228. |
| [6] | Cordeiro, G. and Lemonte, J. (2011) "The Beta-Half-Cauchy Distribution", Journal of Probability and Statistics, Volume 2011, Article ID 904705, p.1-18. |
| [7] | Eugene, N., Lee, C., Famoye, F. (2002) "Beta-normal distribution and its applications" Commun.Statist. - Theory and Methods 31:497-512. |
| [8] | Gradshteyn, I.S., Ryzhik, I.M. (2000) "Table of integrals, series, and products" Academic Press, San Diego. |
| [9] | Gupta, A.K., Nadarajah, S. (2004) "On the moments of the beta normal distribution" Commun. Statist. - Theory and Methods 33:1-13. |
| [10] | Jafari, A. & Tahmasebi, S. and Alizadeh, M. (2014) "The Beta-Gompertz Distribution", Revista Colombiana de Estadística, June, volumen 37, no. 1, pp. 139-156. |
| [11] | Jones, M.C. (2004) "Families of distributions arising from distributions of order statistics" Test 13:1-43. |
| [12] | Merovci, F. and Sharma, V. (2014) "The Beta-Lindley Distribution: Properties and Applications", Journal of Applied Math. , Volume 2014, Article ID 198951, p.1-10. |
| [13] | Nadarajah, S., Gupta, A.K. (2004) "The beta Frechet distribution"; Far East Journal of Theoretical Statistics 14:15-24. |
| [14] | Nadarajah, S., Kotz, S. (2004) "The beta Gumbel distribution" Math. Prob. Eng. 10:323-332. |
| [15] | Nadarajah, S. and Kotz, S. (2005) "The beta exponential distribution", Reliability Engineering and System Safety 91:689-697. |
| [16] | Rajab, M. & Aleem, M. & Nawaz, T. and Daniyal, M. (2013) "On Five Parameter Beta Lomax Distribution", Journal of Statistics, Volume 20, 2013. pp. 102-118. |
| [17] | Zea, L. & Silva, R. & Bourguignon, M. & Santos, A. and & Cordeiro, G. (2012) "The Beta Exponentiated Pareto Distribution with Application to Bladder Cancer Susceptibility"; International Journal of Statistics and Probability; Vol. 1, No. 2; p. 8-19. |

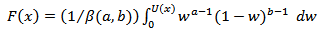
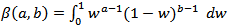 is the beta function. The class of distributions (1) has an increased attention after the works by Eugene et al. (2002) and Jones (2004) [11]. Application of
is the beta function. The class of distributions (1) has an increased attention after the works by Eugene et al. (2002) and Jones (2004) [11]. Application of 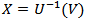 to the random variable V following a beta distribution with parameters a and b, V ∼B(a, b) say, yields X with cdf (1). Eugene et al. (2002) defined the beta normal (BN) distribution by taking U(x) to be the cdf of the normal distribution and derived some of its first moments. General expressions for the moments of the BN distribution were derived (Gupta and Nadarajah, 2004) [9]. Nadarajah and Kotz (2004) [14] also introduced the beta Gumbel (BG) distribution by taking U(x) to be the cdf of the Gumbel distribution and provided closed-form expressions for the moments, the asymptotic distribution of the extreme order statistics and discussed the maximum likelihood estimation procedure. Nadarajah and Gupta (2004) [13] introduced the beta Frechet (BF) distribution by taking U(x) to be the Frechet distribution, derived the analytical shapes of the probability density function (pdf) and the hazard rate function and calculated the asymptotic distribution of the extreme order statistics. However, they do not investigate expressions for its moments and the information matrix which we do in this paper. Also, Nadarajah and Kotz (2005) [15] worked with the beta exponential (BE) distribution and obtained the moment generating function, the first four cumulants, the asymptotic distribution of the extreme order statistics and discussed the maximum likelihood estimation. Barreto-Souza, Santos and Cordeiro (2010).[4] introduced the beta generalized exponential distribution (BGE) that includes the beta exponential and generalized exponential distributions as special cases. They provide a comprehensive mathematical treatment of this distribution. They derived the moment generating function and the rth moment thus generalizing some results in the literature. Expressions for the density, moment generating function and rth moment of the order statistics also are obtained also by them. They discussed estimation of the parameters by maximum likelihood and provide the information matrix. They observed in one application to real data set that this model is quite flexible and can be used quite effectively in analyzing positive data in place of the beta exponential and generalized exponential distributions. Amusan (2010) [2] defined and studied a three-parameter beta Maxwell distribution (BM). Various properties of the distribution were also discussed. The method of maximum likelihood was proposed to estimate the parameters of the distribution. Barreto-Souza, Cordeiro and Simas (2011) [3] derived some mathematical properties of the BF distribution in terms of the corresponding properties of the Frechet distribution. They derived also explicit expansions for the ordinary moments and L-moments and obtain the order statistics and their moments. They discussed also maximum likelihood estimation and calculate the information matrix which was not known. The information matrix is easily numerically determined. Two applications to real data sets are given by them to illustrate the potentiality of this distribution. Cordeiro and Lemonte (2011) [6] proposed the beta-half-Cauchy distribution (BHC) for modeling lifetime data. Various explicit expressions for its moments, generating and quantile functions, mean deviations, and density function of the order statistics and their moments are provided. The parameters of the new model are estimated by maximum likelihood, and the observed information matrix is derived. An application to lifetime real data shows that it can yield a better fit than three- and two-parameter Birnbaum-Saunders, gamma, and Weibull models. Zea, Silva, Bourguignon, Santos and Cordeiro (2012) [17] introduced the beta exponentiated Pareto distribution (BEP). Its density and failure rate functions can have different shapes. It contains as special models several important distributions discussed in the literature, such as the beta-Pareto and exponentiated Pareto distributions. They provided a comprehensive mathematical treatment of the distribution and derived expressions for the moments, generating and quantile functions and incomplete and L-moments. An explicit expression for Renyientropy is obtained. The method of maximum likelihood is used for estimating the model parameters and the observed information matrix is derived. The flexibility of the new model is illustrated with an application to a real data set. Castellares, Montenegro and Cordeiro (2013) [5] introduced the beta log-normal distribution (BLO) for which the log-normal distribution is a special case. Various properties of the new distribution are discussed by them. Expansions for the cumulative distribution and density functions that do not involve complicated functions are derived. They obtained expressions for its moments and for the moments of order statistics. The estimation of parameters is approached by the method of maximum likelihood and the expected information matrix is derived. The new model is quite flexible in analyzing positive data as an important alternative to the gamma, Weibull, generalized exponential, beta exponential and Birnbaum-Saunders distributions. The flexibility of the new distribution is illustrated in an application to a real data set. Rajab, Aleem, Nawaz and Daniyal (2013) [16] developed a new five parameter Beta Lomax Distribution (BLO) from a three parameter Lomax Distribution. They developed expressions for the rth moment; Skewness and Kurtosis of three parameters Lomax, and five parameters Beta Lomax Distribution. At the end, the Maximum Likelihood Estimators (MLE) of the parameters is obtained also. Merovci and Sharma (2014) [12] introduced beta-Lindley distribution that extends the Lindley distribution (BL). They provided a comprehensive mathematical treatment of this distribution. They derived the moment generating function and the rth moment thus, generalizing some results in the literature. Expressions for the density, moment generating function, and rth moment of the order statistics also are obtained. Further, they also discussed estimation of the unknown model parameters in both classical and Bayesian setup. The usefulness of the new model is illustrated by means of two real data sets. Jafari, Tahmasebi and Alizadeh (2014) [10] introduced a new four-parameter generalized version of the Gompertz model which is called Beta-Gompertz (BG) distribution. It includes some well-known lifetime distributions such as Beta-exponential and generalized Gompertz distributions as special sub-models. Some mathematical properties of the new distribution, such as closed-form expressions for the density, cumulative distribution, hazard rate function, the kth order moment, moment generating function, Shannon entropy, and the quantilemeasure are provided. They discussed maximum likelihood estimation of the BG parameters from one observed sample and derive the observed Fisher’s information matrix. A simulation study is performed in order to investigate the properties of the proposed estimator. At the end, in order to show the BG distribution flexibility, an application using a real data set is presented. We can write (1) as,
to the random variable V following a beta distribution with parameters a and b, V ∼B(a, b) say, yields X with cdf (1). Eugene et al. (2002) defined the beta normal (BN) distribution by taking U(x) to be the cdf of the normal distribution and derived some of its first moments. General expressions for the moments of the BN distribution were derived (Gupta and Nadarajah, 2004) [9]. Nadarajah and Kotz (2004) [14] also introduced the beta Gumbel (BG) distribution by taking U(x) to be the cdf of the Gumbel distribution and provided closed-form expressions for the moments, the asymptotic distribution of the extreme order statistics and discussed the maximum likelihood estimation procedure. Nadarajah and Gupta (2004) [13] introduced the beta Frechet (BF) distribution by taking U(x) to be the Frechet distribution, derived the analytical shapes of the probability density function (pdf) and the hazard rate function and calculated the asymptotic distribution of the extreme order statistics. However, they do not investigate expressions for its moments and the information matrix which we do in this paper. Also, Nadarajah and Kotz (2005) [15] worked with the beta exponential (BE) distribution and obtained the moment generating function, the first four cumulants, the asymptotic distribution of the extreme order statistics and discussed the maximum likelihood estimation. Barreto-Souza, Santos and Cordeiro (2010).[4] introduced the beta generalized exponential distribution (BGE) that includes the beta exponential and generalized exponential distributions as special cases. They provide a comprehensive mathematical treatment of this distribution. They derived the moment generating function and the rth moment thus generalizing some results in the literature. Expressions for the density, moment generating function and rth moment of the order statistics also are obtained also by them. They discussed estimation of the parameters by maximum likelihood and provide the information matrix. They observed in one application to real data set that this model is quite flexible and can be used quite effectively in analyzing positive data in place of the beta exponential and generalized exponential distributions. Amusan (2010) [2] defined and studied a three-parameter beta Maxwell distribution (BM). Various properties of the distribution were also discussed. The method of maximum likelihood was proposed to estimate the parameters of the distribution. Barreto-Souza, Cordeiro and Simas (2011) [3] derived some mathematical properties of the BF distribution in terms of the corresponding properties of the Frechet distribution. They derived also explicit expansions for the ordinary moments and L-moments and obtain the order statistics and their moments. They discussed also maximum likelihood estimation and calculate the information matrix which was not known. The information matrix is easily numerically determined. Two applications to real data sets are given by them to illustrate the potentiality of this distribution. Cordeiro and Lemonte (2011) [6] proposed the beta-half-Cauchy distribution (BHC) for modeling lifetime data. Various explicit expressions for its moments, generating and quantile functions, mean deviations, and density function of the order statistics and their moments are provided. The parameters of the new model are estimated by maximum likelihood, and the observed information matrix is derived. An application to lifetime real data shows that it can yield a better fit than three- and two-parameter Birnbaum-Saunders, gamma, and Weibull models. Zea, Silva, Bourguignon, Santos and Cordeiro (2012) [17] introduced the beta exponentiated Pareto distribution (BEP). Its density and failure rate functions can have different shapes. It contains as special models several important distributions discussed in the literature, such as the beta-Pareto and exponentiated Pareto distributions. They provided a comprehensive mathematical treatment of the distribution and derived expressions for the moments, generating and quantile functions and incomplete and L-moments. An explicit expression for Renyientropy is obtained. The method of maximum likelihood is used for estimating the model parameters and the observed information matrix is derived. The flexibility of the new model is illustrated with an application to a real data set. Castellares, Montenegro and Cordeiro (2013) [5] introduced the beta log-normal distribution (BLO) for which the log-normal distribution is a special case. Various properties of the new distribution are discussed by them. Expansions for the cumulative distribution and density functions that do not involve complicated functions are derived. They obtained expressions for its moments and for the moments of order statistics. The estimation of parameters is approached by the method of maximum likelihood and the expected information matrix is derived. The new model is quite flexible in analyzing positive data as an important alternative to the gamma, Weibull, generalized exponential, beta exponential and Birnbaum-Saunders distributions. The flexibility of the new distribution is illustrated in an application to a real data set. Rajab, Aleem, Nawaz and Daniyal (2013) [16] developed a new five parameter Beta Lomax Distribution (BLO) from a three parameter Lomax Distribution. They developed expressions for the rth moment; Skewness and Kurtosis of three parameters Lomax, and five parameters Beta Lomax Distribution. At the end, the Maximum Likelihood Estimators (MLE) of the parameters is obtained also. Merovci and Sharma (2014) [12] introduced beta-Lindley distribution that extends the Lindley distribution (BL). They provided a comprehensive mathematical treatment of this distribution. They derived the moment generating function and the rth moment thus, generalizing some results in the literature. Expressions for the density, moment generating function, and rth moment of the order statistics also are obtained. Further, they also discussed estimation of the unknown model parameters in both classical and Bayesian setup. The usefulness of the new model is illustrated by means of two real data sets. Jafari, Tahmasebi and Alizadeh (2014) [10] introduced a new four-parameter generalized version of the Gompertz model which is called Beta-Gompertz (BG) distribution. It includes some well-known lifetime distributions such as Beta-exponential and generalized Gompertz distributions as special sub-models. Some mathematical properties of the new distribution, such as closed-form expressions for the density, cumulative distribution, hazard rate function, the kth order moment, moment generating function, Shannon entropy, and the quantilemeasure are provided. They discussed maximum likelihood estimation of the BG parameters from one observed sample and derive the observed Fisher’s information matrix. A simulation study is performed in order to investigate the properties of the proposed estimator. At the end, in order to show the BG distribution flexibility, an application using a real data set is presented. We can write (1) as,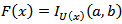
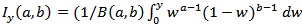 , denotes the incomplete beta function ratio, i.e., the cdf of the beta distribution with parameters a and b. For general a and b, we can express (2) in terms of the well-known hypergeometric function defined by,
, denotes the incomplete beta function ratio, i.e., the cdf of the beta distribution with parameters a and b. For general a and b, we can express (2) in terms of the well-known hypergeometric function defined by, 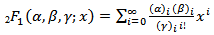 Where
Where 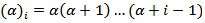 denotes the ascending factorial. We obtain,
denotes the ascending factorial. We obtain,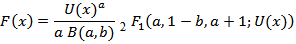 The properties of the cdf, F(x) for any beta U distribution defined from a parent
The properties of the cdf, F(x) for any beta U distribution defined from a parent 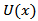 in (1), could, in principle, follow from the properties of the hypergeometric function which are well established in the literature; see, for example, Section 9.1 of Gradshteyn and Ryzhik (2000) [8]. The probability density function (pdf) corresponding to (1) can be written in the form,
in (1), could, in principle, follow from the properties of the hypergeometric function which are well established in the literature; see, for example, Section 9.1 of Gradshteyn and Ryzhik (2000) [8]. The probability density function (pdf) corresponding to (1) can be written in the form,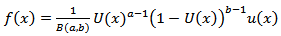
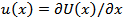 is the pdf of the parent distribution. The pdf
is the pdf of the parent distribution. The pdf 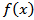 will be mosttractable when the functions
will be mosttractable when the functions 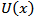 and
and 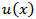 have simple analytic expressions as is the caseof the MOEU distribution. The cdf and pdf of the Marshall Olkin Extended Uniform distribution (MOEU) distribution are, respectively [1],
have simple analytic expressions as is the caseof the MOEU distribution. The cdf and pdf of the Marshall Olkin Extended Uniform distribution (MOEU) distribution are, respectively [1],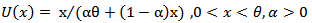
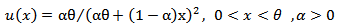
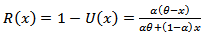
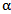 is the shape parameter and
is the shape parameter and 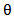 is the scale parameter of the distribution.The hazard rate function of MOEU
is the scale parameter of the distribution.The hazard rate function of MOEU 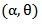 distribution is,
distribution is,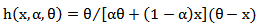
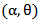 distribution is,
distribution is,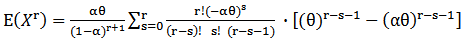
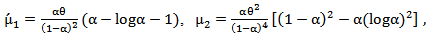
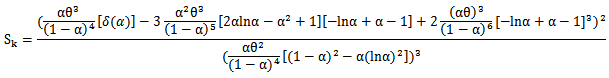 Where,
Where, 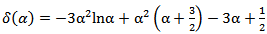 ,
, 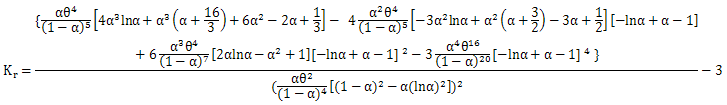 The coefficient of variation is,
The coefficient of variation is, 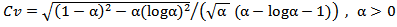 . And it depends only on parameter
. And it depends only on parameter  . The q thquantile of a
. The q thquantile of a  distribution is given by
distribution is given by 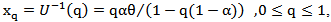 Where
Where 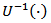 is the inverse distribution function.According to (3) and some of the above properties of a
is the inverse distribution function.According to (3) and some of the above properties of a 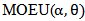 distribution, we get the Beta Marshall Olkin Extended Uniform distribution (BMOEU) with the following pdf,
distribution, we get the Beta Marshall Olkin Extended Uniform distribution (BMOEU) with the following pdf,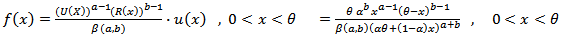
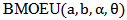 distribution is,
distribution is,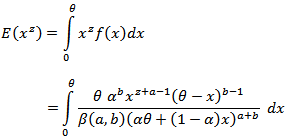 Since,
Since,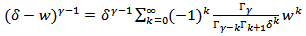
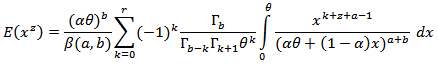 And since,
And since,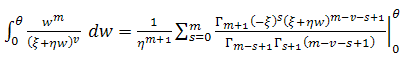
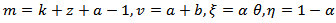 we get,
we get, 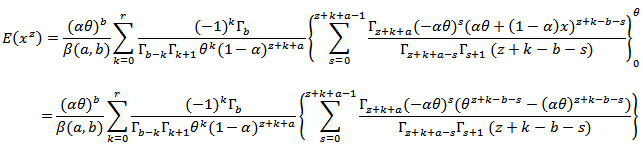
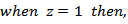 the mean is,
the mean is,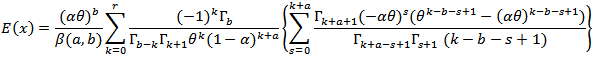
 , one can get the variance
, one can get the variance 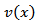 as,
as,
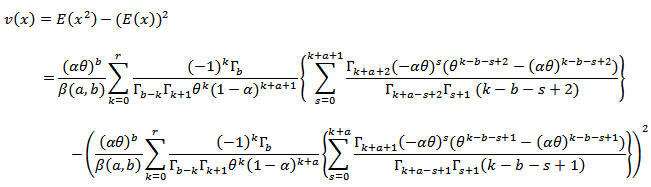
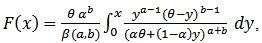
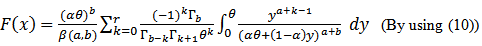 By using (11) with,
By using (11) with, 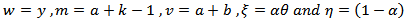 , we get
, we get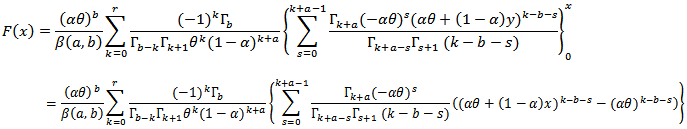
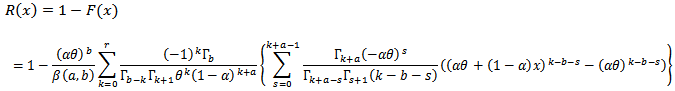
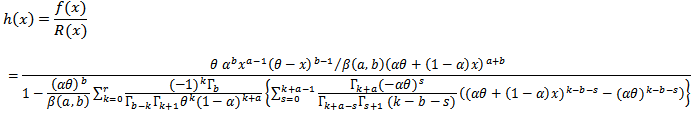
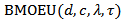 and
and 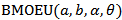 , then, the stress-strength reliability model is,
, then, the stress-strength reliability model is,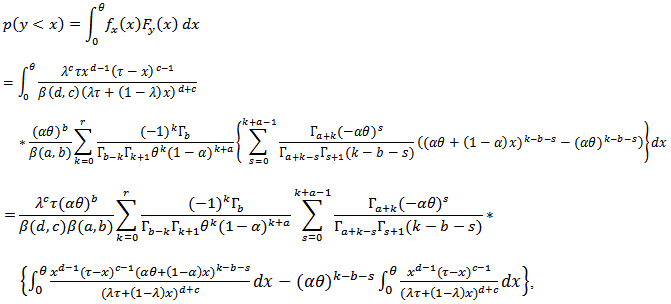 Below, we'll solve integrals inside the brackets above each one separately, so the solution of the first integral is,
Below, we'll solve integrals inside the brackets above each one separately, so the solution of the first integral is,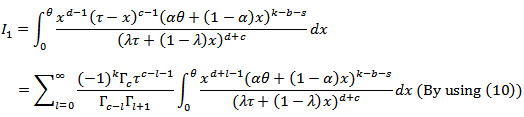 Since,
Since,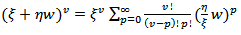
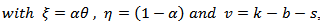 we get,
we get, 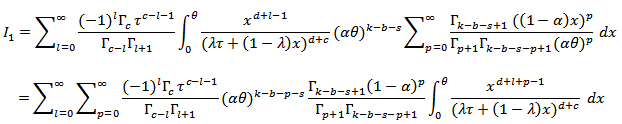 Since,
Since, 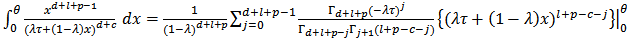 by using (11) with
by using (11) with 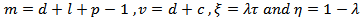 we get,
we get,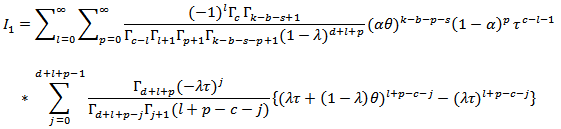 The solution of the second integral is,
The solution of the second integral is,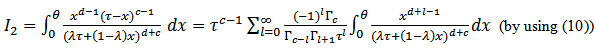 By using (11) with,
By using (11) with, 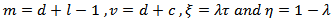 , we get,
, we get,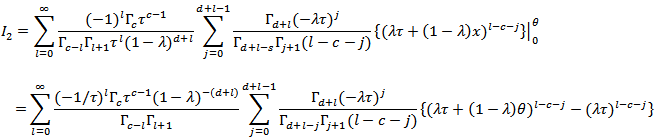 Finally the stress-strength reliability is
Finally the stress-strength reliability is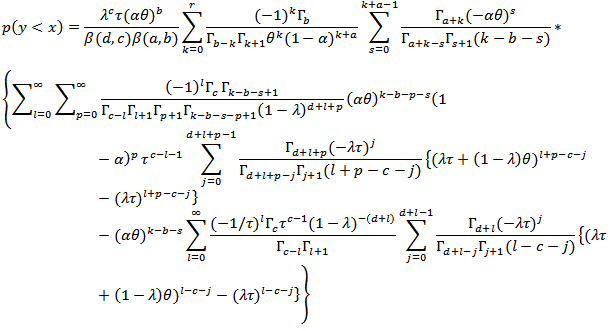
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML