1. Introduction

The design of solar energy conversion systems requires accurate information about the availability of total solar radiation at the desired location. Measuring the solar radiation in the requested site is the best way to obtain representative data. Unfortunately, measured solar radiation data are not available for many locations, especially in developing countries. Therefore, modeling is a proper solution for estimation of the solar radiation at the locations where measurements are not available, taking into account the amount of solar radiation received in the clear-sky condition and applying a factor that parameterizes attenuation caused by cloudiness. In addition to the design of solar energy conversion systems, values of the local global solar radiation are used in most models simulating crop growth and are also necessary for many applications, such as estimation of the evapotranspiration, and architectural design. [1-3].

The intensity of the solar radiation reaching the earth’s surface could be affected by the air mass as well as the weather conditions such as the extent of cloud cover and atmospheric turbidity. On a clear day, the radiation reaching the earth’s surface is reduced by 30%, while it could be reduced by 90% on a hazy or cloudy day. Therefore, solar designed systems perform better on a clear day. So, it is essential to ascertain the estimation of radiation to a surface on a clear day in a particular location using either models or experimental measurements. [4,5]

Clear-sky global solar radiation provides information about the maximum possible magnitude of the solar resource available at a location of interest. Clear sky global solar radiation can be assessed using empirical models [6-12] or physical models [13-15]. Many authors were interested in calculating the clear-sky global solar radiation. For example, The Adnot model, [10], is modified to get an accurate clear-sky global horizontal irradiance for Singapore [17]. The three models, Ineichen-Perez (I-P), European Solar Radiation Atlas model (ESRA), multilayer perceptron neural network (MLPNN), and radial basis function neural network (RBFNN) were tested using solar irradiance data measured at eight different locations in South Africa. The author found that The I-P model showed the best performance [18]. The ASHRAE Clear-sky model was used for calculating the clear-sky global horizontal solar radiation in Aligarh, India. The author stated that the ASHRAE model is suitable to estimate the hourly solar radiation [19]. Eight measurement stations were used in different locations in Saudi Arabia to obtain new clearness factors for the ASHRAE model. The modified ASHRAE model is found to be reasonable for estimating the radiation components, especially for the monthly values, while the daily profile could have some differences [20]. A model was developed to calculate the hourly solar radiation falling on a horizontal surface in Beni-Suef City, Egypt via a validated simulation model [21]. A clear-sky solar radiation model based on the latest mathematical equations published in European Solar Radiation Atlas was implemented and used with a digital elevation model developed based on the Shuttle Radar Topography Mission database to estimate the clear-sky solar radiation in Romanian territory [3]. Hottel’s model was used for estimating the daily average values of the clear-sky direct normal irradiance in Jeddah-Saudi Arabia. The authors indicated that the average daily values obtained using Hottel’s model, and that obtained from measured ones are in good agreement [22]. The monthly average hourly global solar radiation was calculated in Yemen as a sum of the direct component calculated by the Hottel’s model and the diffuse component calculated by the Liu and Jordan model [23]. The Hottel’s model was tested experimentally for calculating the clear-sky direct solar radiation in Makurdi, Nigeria. The authors concluded that there is slim suitability of Hottel’s model in Makurdi location due to the effect of the climatic factors such as humidity, seasonal variation, and weather because they were not directly taken into consideration in the development of the model [4].

In this work, we attempt to test the estimation of the global clear-sky solar radiation in Qena/Egypt using Hottel’s model for calculating the direct component and Liu and Jordan’s model for calculating the diffuse component. The estimated hourly, daily values, and monthly average values will be compared with the corresponding measured clear-sky global solar radiation values at Qena/ Egypt during the period from 2004 to 2012. The model performance is tested using the appropriate statistical analysis.

2. Data and Methodology

The data used in this study have been measured by the Egyptian national weather authority in the atmospheric laboratory located on the campus of the South Valley University in Qena (26.20 N°; 32.75 E°). Global solar radiation data on a horizontal surface during the period from 2004 to 2012 have been measured using the Precision Spectral Pyranometer (PSP) No. 16317IS, with a spectral range of 0.285 to 2.8 μm. The Combilog Datalogger (No.1020, TH. Friedrichs & CO “Germany”) is used for recording the values of the hourly global solar radiation data. The PSP instrument is calibrated each year. The absolute accuracy of calibration is ±3–4%. Cloud cover is recorded visually for each hour.

Qena is a small city in Upper Egypt (26.20 N, 32.75 E, 97 m asl). It is characterized by a very hot and dry summer and relatively cold winter. The average daily maximum temperature reaches 40°C in summer and 25° in winter. The average daily minimum relative humidity is about 17% in summer and 26% in winter [24,25]. There is almost no rain in Qena. The winter average maximum mixing height is 1418 m while the summer average maximum mixing height is 2481 m [26]. The area receives a large amount of solar radiation, especially in the summer, where the monthly average daily global solar radiation reaches about 27 MJ/ m² in July as stated in [27].

The global solar radiation is the sum of the beam radiation and the diffuse radiation. The beam radiation transmitted through the atmosphere in clear-sky conditions in Qena/Egypt has been calculated using Hottel’s model [28], where, the atmospheric transmittance for beam radiation Ib is given as

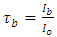(1)

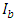where, is the hourly beam radiation incident normal to the surface, and 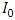is the extraterrestrial hourly beam radiation given as

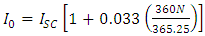(2)

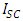where is the solar constant, its value is considered as 1367 W/m², and N is the day number in the year, it varies from 1 to 365.

The clear-sky normal beam radiation is given by [29]

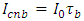(3)

The clear-sky beam radiation on a horizontal surface is given as

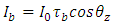(4)

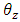where is the zenith angle and can be calculated as

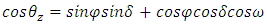(5)

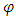where is the latitude of the location,

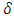is the declination angle of the sun and can be calculated as

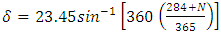(6)

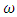is the hour angle and can be determined from the following equation

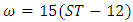(7)

where ST is solar time in hours.

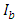The atmospheric transmittance for the beam radiation for clear-sky conditions is given by Hottel’s model in the form

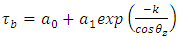(8)

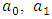where and 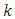are constants determined using the correction factors for different climate types as [29]:

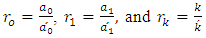(9)

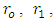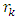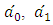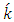The values of and for subtropical summer locations with an altitude less than 2.5 km are 0.99, 0.99, and 1.01, respectively. and can be determined from the relations:

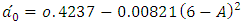(10)

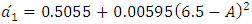(11)

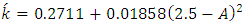(12)

Where A is the altitude of the observer in kilometres

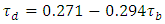Liu and Jordan’s model [30], as seen in eq. (13) is used to calculate diffuse clear-sly radiation on a horizontal surface, and then added to the beam radiation calculated by Hotel’s method to obtain the clear-sky hourly global solar radiation

(13)

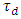where is the ratio of diffuse radiation to the extraterrestrial beam radiation on the horizontal plane.

2.1. Statistical Evaluation

To ensure the accuracy of calculation of the clear-sky global solar radiation, some statistical measures are used; the used measures are the mean bias error (MBE), mean absolute bias error (MABE), root mean square errors (RMSE), model efficiency (ME), modeling index (d) and t-statistic test (t). These indices are defined as the following:

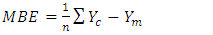(14)

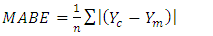(15)

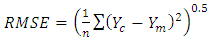(16)

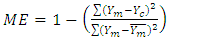(17)

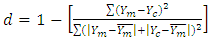(18)

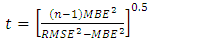(19)

In the (MBE), (MABE) and (RMSE) statistical tests, the smaller the value, the better the model performance, while values of (ME) and (d) closer to 1 indicate the superior model performance [31-34]. P-Value calculated using eq. 19 must be more than 0.05 so we cannot reject the null hypothesis, and concluding that there is no significant difference between the measured and calculated mean values.

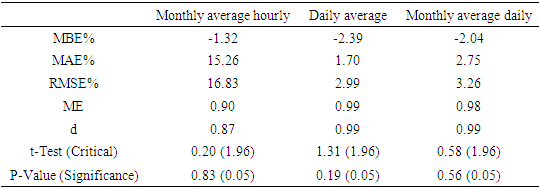
3. Results and Discussion

3.1. Verification of the Monthly Average Hourly Clear-Sky Global Solar Radiation (CSGSR)

Figure 1 shows the variation of the measured and the calculated values of the monthly average hourly CSGSR during the period from 2004 to 2012 in Qena/Egypt. It is graphically obvious that the measured and the calculated values are close to each other. So, we expect that Hottel’s model and Liu and Jordan’s model can represent the hourly variation of the CSGSR.

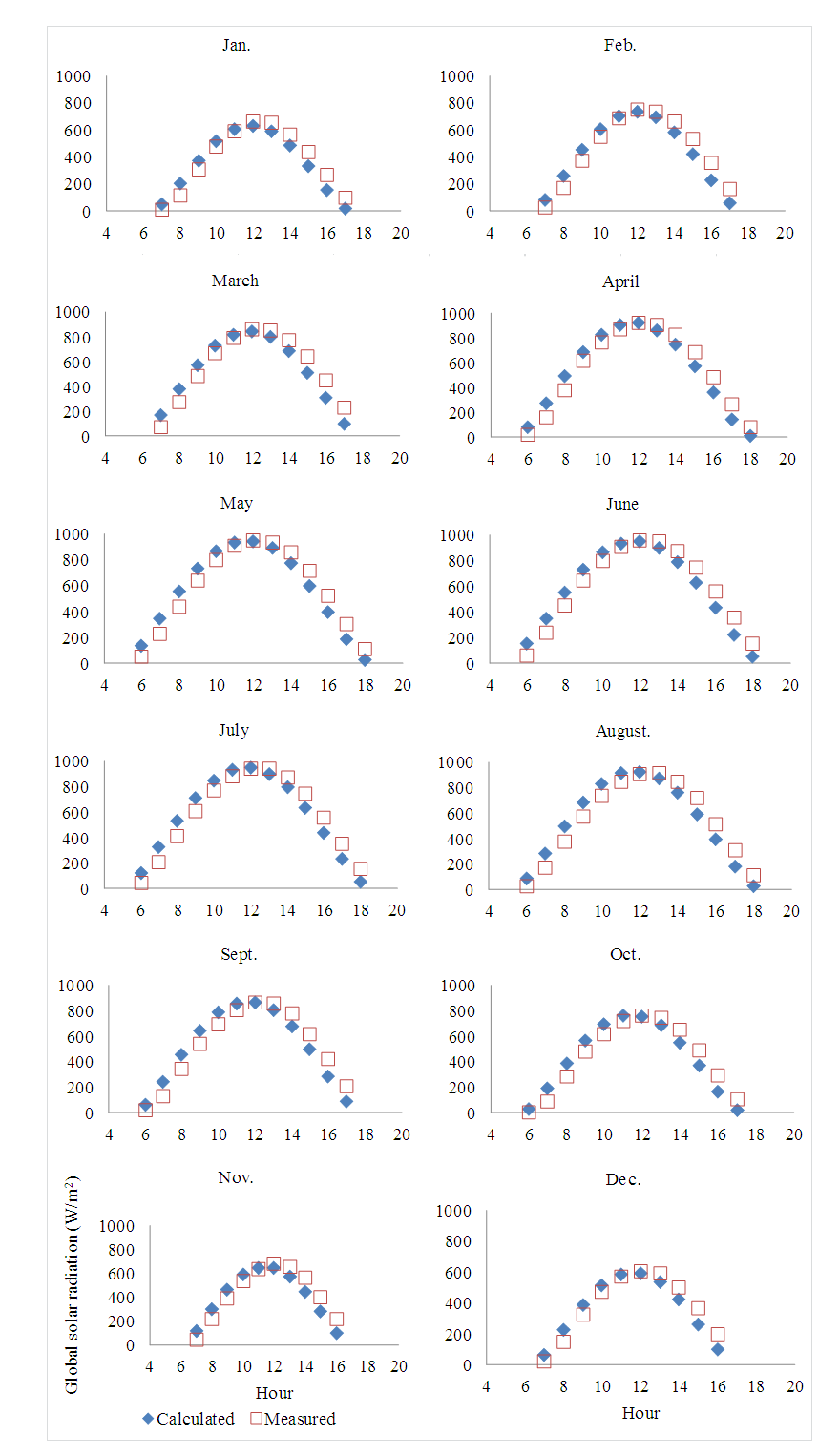Figure 1. Variation of the measured and the calculated monthly average hourly clear-sky global solar radiation (W/m2) in Qena during the period from 2004 to 2012

To test the validity of the Hottel’s Model and Liu and Jordan’s Model for estimating the CSGSR, the two models are used to calculate the hourly values of the global solar radiation. Then, the calculated values of the monthly average hourly CSGSR are compared with the corresponding measured ones during the period from 2004 to 2012. There were no data during the year 2005 as a result of the malfunction of the instrument. The total numbers of used clear days were 2463 days. Figure 2 declares the scatterplot between the measured and the calculated values. A good correlation (0.95) between the measured and the calculated values are found. From the figure we can notice that the calculated hourly values of the global solar radiation are more deviated from the measured ones for the values less than 600 w/m², these values are recorded during the morning and the evening hours, while the calculated values are more close to the measured ones for the values which are more than 600 W/m², these values are generally recorded at noon and around noon hours. This phenomenon may be attributed to the hourly variation of the weather elements such as the relative humidity and the atmospheric turbidity.

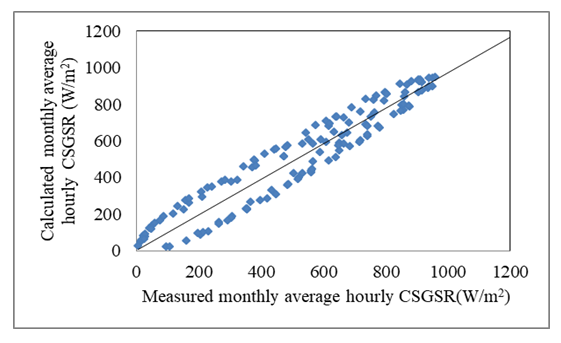Figure 2. Relationship between the measured and the calculated monthly average hourly clear-sky global solar radiation in Qena during the period from 2004 to 2012

Figure 3 represents the relative deviation percentage (%) of the calculated monthly average hourly CSGSR from measured ones at Qena during the study period; this figure emphasis that the relative deviation percentage (%) increases for the morning and afternoon hours.

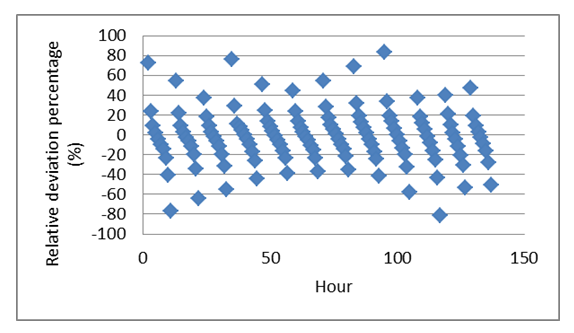Figure 3. Relative deviation percentages (%) of the calculated monthly average hourly CSGSR from measured ones at Qena during the study period

The frequency distribution of the relative deviation of the calculated CSGSR from measured ones at Qena through the study period is shown in figure 4. From the figure, we can notice that 38% and 60% of the calculated data have deviations ±10% and ±20%, respectively, while, 40% of the calculated data have relative deviations more than 20%. From the two figures, we can deduce that the Hottel’s Model and Liu and Jordan’s Model tend to estimate fewer values than the measured ones, the less estimated hourly values are found in about 53% of the calculated data, while the more estimated values are only about 47%.

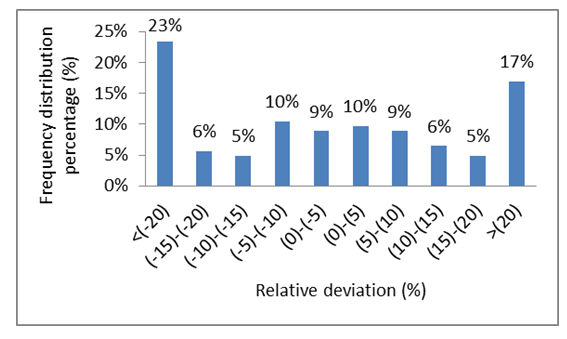Figure 4. Frequency distribution of the relative deviation of the monthly average hourly CSGSR from measured ones at Qena during the period of study

Table 1 illustrates the statistical parameters calculated for the monthly average hourly, average daily, and monthly average daily calculated values of global solar radiation using the Hottel’s Model and the Liu and Jordan’s Model in Qena during the period of study. We can indicate that the MBE% and MAE% have relatively small values, -1.32% and 15.26%, respectively. The model efficiency ME and the model deterministic d have relatively small values, 0.90 and 0.87, respectively. the calculated significance, P-Value, (0.83) is more than the significance level (0.05), so we cannot reject the null hypothesis, so, there is no significant difference between the measured and calculated mean values. Also, the t-test value (0.20) is less than the tabulated value (1.96). So, we can say that the two models combined can be used to estimate the monthly average hourly CSGSR in Qena.

3.2. Verification of the Average Daily Global Solar Radiation

To test the validity of the Hottel’s Model and the Liu and Jordan’s Model for calculating the average daily values of the CSGSR, the daily values of the CSGSR are calculated from the corresponding hourly values for each day, then, the average daily values of the CSGSR are calculated during the period from 2004 to 2012. Fig. 5 shows the daily variation of the calculated and measured clear-sky global solar radiation for each year during the period from 2004 to 2012, it is clear that the models can represent strongly the daily variation of the clear-sky global solar radiation during the different years. Fig. 6 illustrates the relationship between the measured and the calculated average daily values of the CSGSR during the period from 2004 to 2012. High correlation coefficient (0.97) between the measured and calculated values is found.

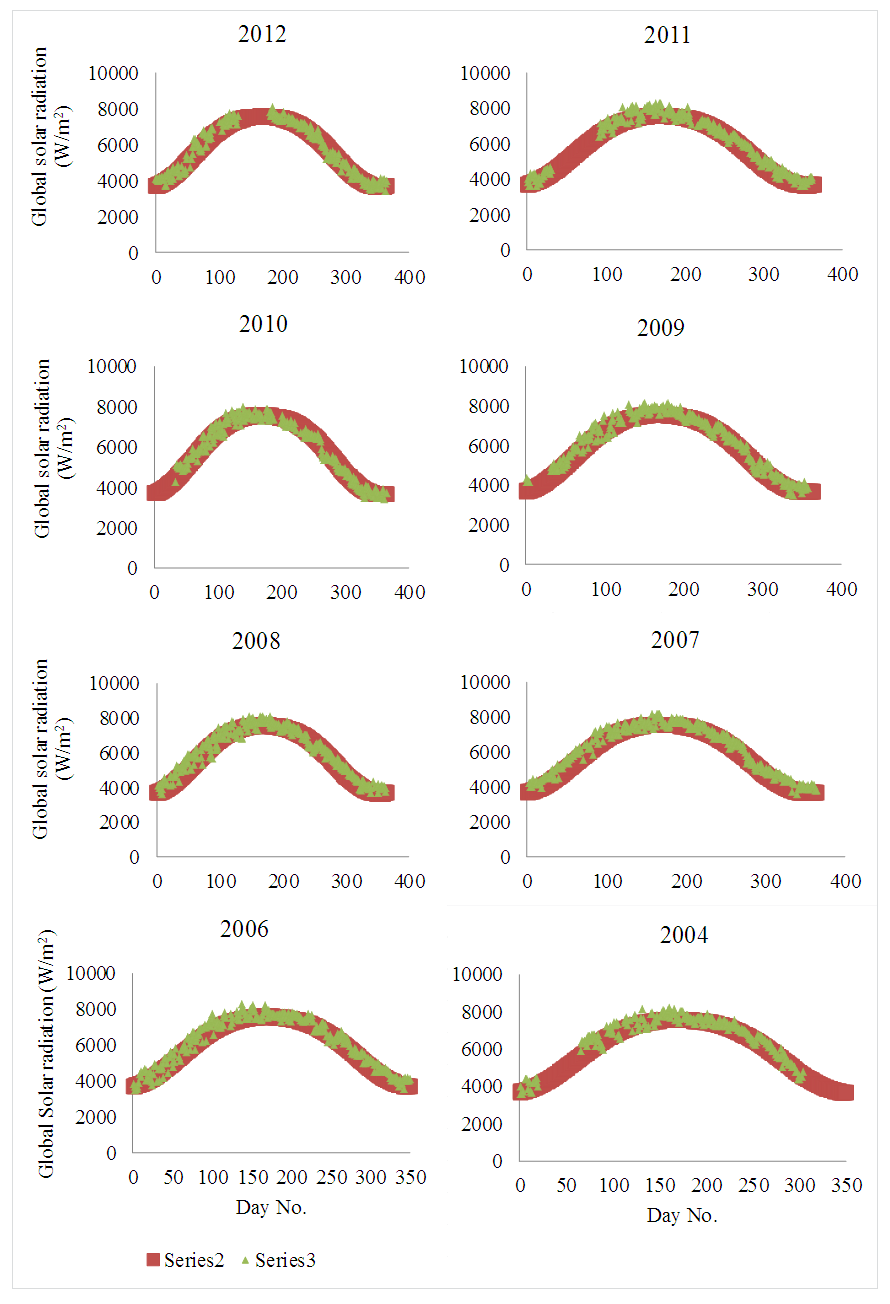Figure 5. Daily variation of the calculated and measured clear-sky global solar radiation during the period from 2004 to 2012 in Qena/Egypt

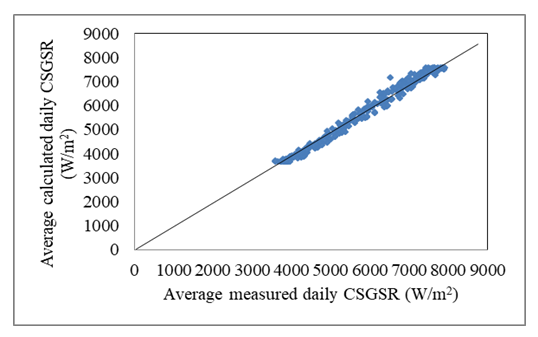Figure 6. Relationship between averages of measured daily CSGSR and calculated values in Qena during the period of study

For investigating the accuracy of estimation, Figure 7 is prepared to represent the relative deviation percentage (%) of the calculated average daily values of the CSGSR from measured ones at Qena during the period of study. We can notice that the relative deviations have seasonal variation. Where, the relative deviations increased in winter and autumn while decreased in the summer season. 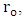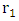This may be attributed to the use of Hottel’s model correction factors, and 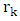for subtropical summer locations as indicated in section 2. Even though, the deviations during winter and autumn are not exceeded ±10%.

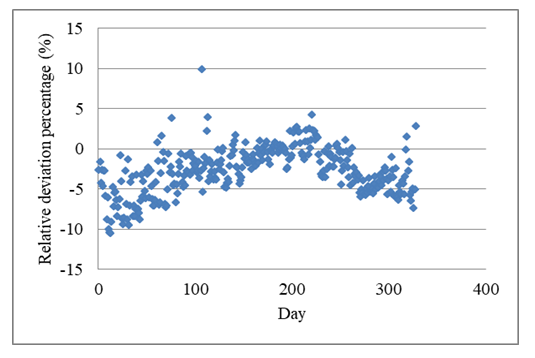Figure 7. Relative deviation percentages (%) of the calculated average daily values of CSGSR from measured ones at Qena during the period from 2004 to 2012

Figure 8 represents the frequency distribution percentages of the relative deviation of the calculated average daily values of the CSGSR from measured ones. From the figure, we can deduce that more than 77% of the relative deviation percentages are within ±5% and about 99% are within ±10%.

Figure 8. Frequency distribution of the relative deviation of calculated average daily values of CSGSR from measured ones at Qena during the study period

Figures 7 and 8 indicate that the Hottel’s Model and the Liu and Jordan’s Model generally tend to underestimate the average daily CSGSR values, the underestimated values are found in about 70% of the considered clear days.

The statistical analysis related to the average daily values is illustrated in table 1. We can notice that the values of MBE, MAE, and RMSE are small, -2.39, 1.70, and 2.99, respectively, while the values of the ME and d are very high, 0.99 for each. The calculated t-test value, 1.31 is smaller than the tabulated value of 1.96. Also, the calculated significance, P-Value, 0.19, is found to be greater than 0.05. So, there is no significant difference between the measured and the calculated mean daily values.

Table 1. Statistical analysis of the monthly average hourly, daily average, and monthly average daily calculated values of global solar radiation using the Hottel’s Model and Liu and Jordan’s Model in Qena during the period from 2004 to 2020

3.3. Verification of the Monthly Average Global Solar Radiation

Figure 9 illustrates the relationship between the measured and the calculated monthly average values of the CSGSR during the period from 2004 to 2012. An excellent correlation (0.99) between the measured and calculated values is found.

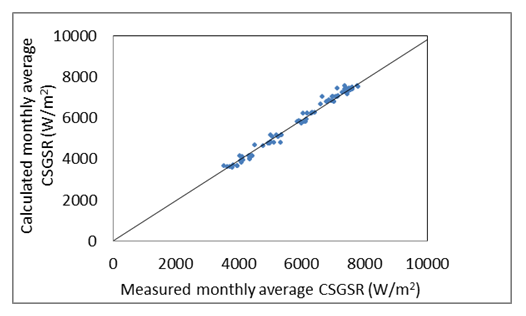Figure 9. Relationship between the measured monthly average global solar radiation and the calculated corresponding values in Qena during the period from 2004 to 2012

Figure 10 represents a scatterplot of the relative deviation percentages (%) of the calculated monthly average CSGSR from the measured ones at Qena through the study period. We can see that most of the values are less estimated. Figure 11 illustrates the frequency distribution of that relative deviations, we can notice that about 83% of the frequency distribution percentages have relative deviations within ±5%, and 100% of the calculated monthly average data have relative deviations within ±10%.

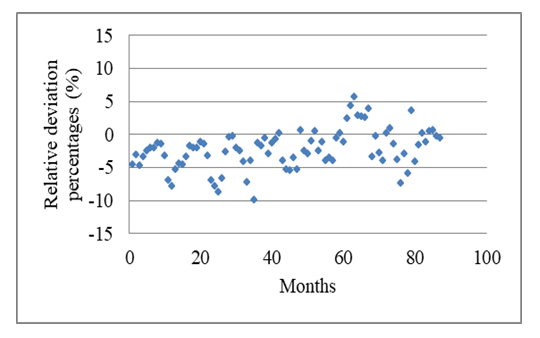Figure 10. Relative deviation percentages (%) of the calculated monthly average global solar radiation from the measured ones at Qena during the period from 2004 to 2012

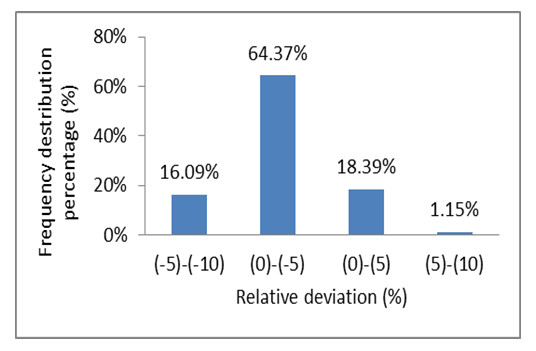Figure 11. Frequency distribution of the relative deviation of calculated monthly average global solar radiation from measured ones at Qena through the study period

The statistical analysis is applied to the calculated monthly average values and illustrated in table 1. We can notice that the values of MBE, MAE, and RMSE are small, -2.04, 2.75, and 3.26, respectively, while the values of the ME and d are very high, 0.98 and 0.99, respectively. Besides, the calculated t-test value, 0.58 is smaller than the tabulated value of 1.96. Also, The P-Value, 0.56, is more than the significance level 0.05, so, there is no significant difference between the measured and the calculated monthly average values.

4. Conclusions

In this work, the clear-sky global solar radiation CSGSR is estimated in Qena/Egypt using the Hottel’s Model for calculating the component of clear-sky direct solar radiation and the Liu and Jordan’s model for calculating the component of diffuse clear-sky radiation on a horizontal surface. The calculated values were in different time scales, monthly average hourly, average daily, and monthly average. The calculated values are compared with the corresponding measured clear-sky data of the global solar radiation during the period from 2004 to 2012 at Qena/Egypt. Different statistical performance measures are used to ensure the validity of the two models to calculate the CSGSR. It is found that the two models combined can represent the CSGSR in Qena at different time scales. Where, the correlation coefficient between the measured and the calculated values are high, and the error measure parameters, MBE, MABE, and RMSE values are small for different time scales. Also, the model efficiency ME, and the modeling index (d) have high values. The t-statistic test (t) indicated that there is no significant difference between the calculated and the measured values during the different time scales. So that, the Hottel’s Model for calculating the component of clear-sky direct solar radiation and the Liu and Jordan’s model for calculating the component of diffuse clear-sky radiation on a horizontal surface can be used safely for calculating the CSGSR in Qena/Egypt and in other sites with the same climate characteristics.