1. Introduction

The broad term used to describe the various means of extracting useful information and analysing an image is known as image processing.

Digital image processing [1] and analog image processing constitute the types of image processing. In this paper we practice Digital image processing. Digital Image Processing can be summarized as a set of actions of converting an image into a computable form and carry out operations on it to withdraw important data from the image. It is a rapidly growing technological field that makes practical use of the state of the art machine learning algorithms such as Classification, Pattern Recognition, Feature Extraction.

Digital image processing allows the use of computer algorithms which support the implementation of complex methods and techniques that would be impossible by analog means.

It is being widely used in fields such as machine/robot vision, medical field, pattern recognition, image sharpening, video processing.

Image segmentation [2] is the first step in pre-processing of Image Analysis. It can be visualised as a process of splitting an image into manifold segments. It is commonly used in locating an object from an image or locating lines, curves or edges in images.

Image segmentation [3] can be achieved by Thresholding, Clustering Methods, Histogram based Methods and Active contours or snake is the most commonly used Technique in Image segmentation. In the field of medical images active contours played a wide role [25, 27, 29].

Previous work on research papers show the various object detection techniques [3, 4, 5] for image segmentation based on color, shape and Texture, by using techniques like color histogram, boundary structure model and edge focussing algorithms. Pre-processing Tools like color distance map and input strokes were used to improve the performance of Image segmentation.

In our experiment we performed trials on cotton leaf images for segmentation to check if it converges better in the presence of the GVF force or the VFC force [28, 26]. We have also kept track of the time and iterations taken to converge in presence of these fields and further drawn conclusions.

2. Active Contour

Snakes or Active Contours [6, 7, 21] can be generalized as curves described in an image domain that can shrink or grow due to the Internal and External Forces.

Internal forces are defined within the curve itself, whereas the External forces arise from the image data. These forces ensure that the snake is confined to object boundaries or any other feature in the image.

Active contour models [2, 17] are of two types Parametric Active Contours and Geometric Active Contours.

2.1. Parametric Active Contour

Parametric active contours [8] synthesize parametric curves within the domain of an image and aid them to move towards edges of the object within the image domain.

The energy function of an active contour within the spatial domain of an image involves two forces as its components, namely, external forces and internal forces.

The external forces comprise potential forces and other forces such as pressure forces [9]. Potential forces [10] are calculated as the negative gradient of a potential function. Internal forces are the forces responsible for holding the curve together and preventing the curve from bending too much.

2.2. Geometric Active Contour

The field of medical image computation has made significant use of Geometric Active Contours. Geometric active contours [11, 16, 24] also known as Geodesic active contours perform the actions of breaking the contour and merging them on the basis of occurrences of objects in the given image. Geometric active contours majorly work with functions of the image’s arc length, or the derivatives obtained with respect to these functions.

In our experiments we have adopted to Parametric Active Contour as the convergence speed was much faster compared to Geometric Active Contour.

3. Parametric Snake Model

A snake [8] is a curve x(s) = [x(s),y(s)], where s belongs to the range [0,1]. For a snake model its energy functional can be given as

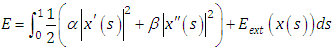(1)

Here, the active contour model’s tension is controlled by α and the model’s rigidity is controlled by β. x’(s) and x’’(s) are the first and second derivative of x(s) respectively. Here the E_ext is obtained from the image.

The total energy of a snake model is the sum of the energy of the internal forces and the external forces, where the external forces tend to act in the direction opposite to that of the internal forces. The snake stops moving when the internal and external energies are at equilibrium. The value of the total energy function E tends to zero at the boundary of the image.

The internal forces and the external forces acting on the image to minimize the total energy function E, must satisfy the Euler’s equation

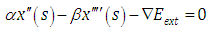(2)

4. Gradient Vector Flow

There are two major challenges [8] with the Active Contour. First the initial snake must be really close to the edge to be detected and snakes have difficulty to converge in the concave regions.

To overcome these challenges a new external force was introduced, whose fields are called GVF fields and the snake that uses the GVF field is called GVF snake [12, 20, 22]. This GVF field pulls the snake towards the object boundary when the snake is closer to the boundary and can converge the snake into concave regions.

Energy minimization function for GVF can be stated as

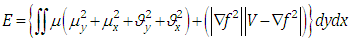(3)

where V(x,y) = {u(x,y), v(x,y)} is the vector field for the GVF force. GVF [13] field can be solved by using Euler’s Lagrange equation

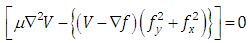(4)

Using Dynamic approach [18] in the above equation and substituting V as a function of x, y and t the equation can be re-written in the following manner:

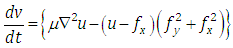(5)

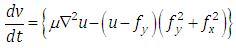(6)

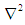where the term in the above two equations is called as Laplacian operator [23]. The second term in the above two equations reduces to zero as the gradient of f(x,y) reaches zero, where f(x,y) is the edge map of the image. The GVF field is obtained from the above two equations with V(x,y) as an External force.

In Figure 1a and Figure 1b we can see the sample leaf image and the converged GVF snake, where the enclosing line represents the GVF snake converging the leaf image.

Figure 1a. This figure shows a sample image and a converged GVF snake

Figure 1b. This figure shows a sample image and a converged GVF snake

5. Vector Field Convolution

One of the important drawbacks [14] of the GVF snake model was the high computational cost. This problem was largely solved with the VFC snake model.

The Vector Field Convolution (VFC) snake model is obtained by replacing the standard external force in the active contour model by the VFC external force [15].

We can calculate the VFC force v(x,y) = [u(x,y), v(x,y)] for an image I(x,y) with the help of the vector field kernel k(x,y) and edge map f(x,y) for the image.

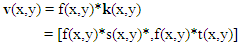Here, the vector field kernel k(x,y) is given by

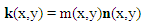Where m(x,y) is the magnitude of the vector at (x,y) and n(x,y) is the unit vector pointing to the origin

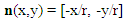Where 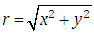is the distance from the origin, except that n(0,0) = [0,0] at the origin.

The images we used in our research were leaf images (with and without noise) and we used a two dimensional vector field.

The magnitude of the vector field kernel is a huge factor deciding the strength of VFC field. The radius of the vector field kernel must be chosen with concern. We chose the gamma value to be 1.8 in these experiments while determining the magnitude of the vector field kernel. There are two types of magnitude functions [14].

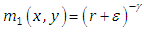(7)

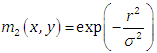(8)

Here γ and σ are parameters to control the decrease ε, is a small constant to avert division by zero at the origin. All the three parameters mentioned above are positive.

The edge map f(x,y) also plays an important role in determining the VFC force field. One of the major positives of the VFC model would be that it takes into account the strength of the features of the image. Stronger features contribute more towards the VFC field compared to the weak features.

In Figure 2a and Figure 2b we can see the sample leaf image and the converged VFC snake, where the enclosing line represents the VFC snake converging the leaf image.

Figure 2a. This figure shows a sample image and a converged VFC snake

Figure 2b. This figure shows a sample image and a converged VFC snake

6. Results and Comparison

6.1. Edge Map

An edge map of an image can be defined as an image that describes and specifies the edges of the image. An edge map of an image can be considered as the result obtained by applying an edge detection filter on the image. The strength and solidity of the edges would depend on the values calculated by the edge detection filter.

Edge Detection is considered as the basic step in image segmentation. The process of edge detection involves a series of methods aimed at spotting points on the image where there is a sudden change in the image brightness (discontinuities). An edge in an image can be defined as a boundary where there is considerable change in physical features such as illumination and visibility.

Some of the popular edge detection techniques include Sobel edge Detection, Canny edge detection, Laplacian of Gaussion (LoG) edge detection [19].

6.2. Sobel Edge Detection

The Sobel operator is a popular edge detection technique which is based on entwining the given image with minimal, numerical filter in the horizontal and vertical directions and is hence computationally cheaper. The Sobel operator uses two 3X3 kernels which entwine over the initial image to compute approximations of the derivatives for both the vertical and horizontal changes.

Figure 3. Finding Edge map using Sobel Edge Map Technique

6.3. Canny Edge Detection

Canny edge detection is a technique involves multiple stages. These include removing or reducing noise from the image, applying the Sobel operator on the smoothed image in both the directions. The following stages involves removing unwanted pixels and non-edges by examining if there values qualify a threshold value.

Figure 4. Finding Edge map using Canny Edge Map Technique

6.4. LoG Edge Detection

The Laplacian of Gaussian (LoG) edge detection technique is quite similar to the Canny edge detection technique which includes similar stages such as noise reduction. Here, a second derivative of the smoothed image is used to detect if a zero valued pixel or edge occurs. The zero valued point indicates the presence of an edge.

Figure 5. Finding Edge map using LoG Edge Map Technique

From the figure 3, 4 and 5 we can see the leaf edges outline are clearer in figure 5 than compare to other edge detection algorithms. Active contours are sensitive to the edges so, if too many edges are present than contour gets attracted towards them. So, LoG edge map will have only the outer edge of the image resulting in good results for segmentation.

As we see from the figures Figure 1, and Figure 2 both the snake models Gradient Vector Flow (GVF) and Vector Field Convolution (VFC) converge well to a large extent over the leaf images.

But the factors of computational cost, precision are of high importance.

In our experiments we found the VFC model converges at a higher speed, with fewer number of iterations. It can be seen from the graph in Figure 6 that the time taken to converge the leaf images using the GVF model is on an average four times larger than the time taken by the VFC model. The graph in Figure 7 represents the larger number of iterations required by the GVF model when compared to the VFC model. Also the variation in the number of iterations required to converge from one leaf image to another in the VFC model was much smaller than the large variation shown by the GVF model. We began with various different values for the parameters of the snake models and concluded that the values of 0.035 and 1 for α and β respectively were the most suitable. We found that one of the major reasons for the faster convergence of the VFC model was due to higher converging speed of the VFC model compared to the GVF model at concave regions. Since the leaf images had nearly three to five concave portions, this feature proved to be critical.

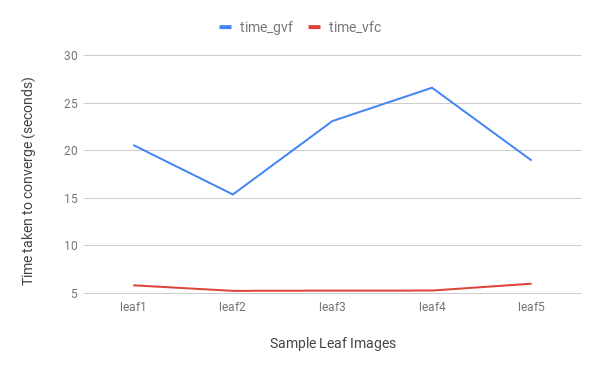Figure 6. A graph representing the time taken by the GVF and VFC models to converge around the leaf images

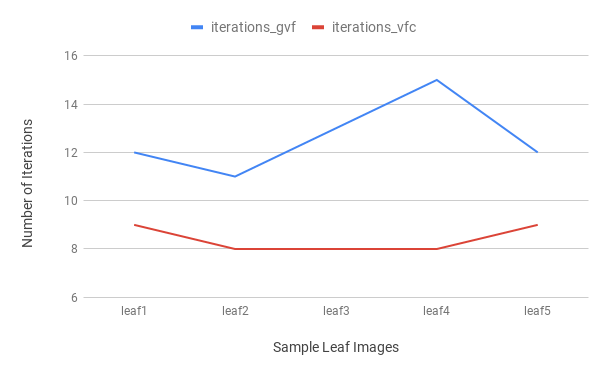Figure 7. A graph represents number of iterations taken by the GVF and VFC models to converge around the leaf images

Also we decided to use the Laplacian filter with the VFC model which helped the model detect the clear edges in the leaf images in lesser time. Two important factors, the number of iterations and the time taken for convergence proved to be in smaller for the VFC model over the GVF model for all the leaf images tested upon by us. Both the models showed linear pattern between the time taken and the number of iterations factors i.e. the time.

Although in the VFC model a single iteration made a difference of less than 0.6 seconds, in the GVF model each iteration towards the end of the converging process made a significant difference of nearly two to four seconds.

Table 1. Table representing the number of iterations and time taken to converge in presence of GVF and VFC for sample images

7. Computational Cost

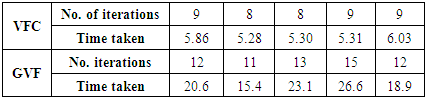
The images that we used were of dimensions 256 X 256. Our experiments were carried out in a Dell Inspiron System. The system ran on an i5 processor, with 16 GB RAM and 2.00 GHZ CPU. The software tool used for the above experiments was MATLAB. It can be said that the number of iterations is the most important factor deciding the computational cost of a snake model. From our work it can be seen that the number of iterations is higher and hence the computational cost of the GVF model is higher than the VFC model.

8. Conclusions

After Immense analysis and research on convergence of active contour on leaf images in the presence of GVF and VFC, we have come to a conclusion that the snake converges faster in terms of number of iterations and the CPU time in presence of VFC. Also the computational cost for GVF is higher than VFC, due to the increased number of iterations and time.