-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Physical Chemistry
p-ISSN: 2167-7042 e-ISSN: 2167-7069
2017; 7(3): 63-69
doi:10.5923/j.pc.20170703.02

Internal Energy Functions of Thermodynamic Systems
Xiaofu Wu
College of Environmental Science and Engineering, Central South University of Forestry and Technology, Changsha, P. R. China
Correspondence to: Xiaofu Wu, College of Environmental Science and Engineering, Central South University of Forestry and Technology, Changsha, P. R. China.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The present work presents a different angle to look into the concepts of internal energy functions of thermodynamic systems. The argument presented is that the total internal energy U of a thermodynamic system consists of two basic components, Uk, the kinetic energy of the material particles moving in the interior space of the system, and Um, the energy stored in other forms inside the materials contained by the system. Internal energy is matter-dependent and energy exchange is thus a process of matter exchange. The expression of U as a function of pressure P or temperature T given volume V does not take Um into account. The relation ∆U=q-w is a path function for closed systems without matter exchange. Work (w) as a path function is not quantitatively related to the change in U as the work done by a system on its surroundings should be equal to the work done by the surroundings on the system. Heat (h) can be either absorbed or released, and heat transfer is a process of mass transfer. The connections of Uk and Um with enthalpy H, entropy S, Helmholtz free energy A and Gibbs free energy G are Uk=H=TS, Um=A=G and U=TS+G.
Keywords: Internal energy, Kinetic energy, Material energy, Enthalpy, Entropy, Free energy
Cite this paper: Xiaofu Wu, Internal Energy Functions of Thermodynamic Systems, Physical Chemistry, Vol. 7 No. 3, 2017, pp. 63-69. doi: 10.5923/j.pc.20170703.02.
Article Outline
1. Introduction
- There have been difficulties to fully understand the concepts of enthalpy H and entropy S though they are generally acknowledged state functions of thermodynamic systems. As a matter of fact the concepts of H and S are not more abstract than that of a thermodynamic system. In textbooks [1-5] used in universities there is no concrete definition of a thermodynamic system concerning its volume V. For ideal gases, V does not appear to be a necessary variable since the total internal energy U depends only on temperature T, disregarding the change in V [1-3].Both H and S are linked to heat uptake q and their incremental values can be determined, respectively, by ∆H=qP and ∆S=qr/T, where the subscripts P and r denote, respectively, constant pressure and reversible process. In later years the Helmholtz free energy A and Gibbs free energy G were further introduced as state functions based on their connections with, respectively, total and nonexpansion work [1-3]. The present study presents a different angle to look into the concepts of these traditionally defined state functions with focus on their heat and work related natures.
2. State Function and Path Function
- The classic mathematical expression of the first law of thermodynamics is
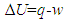 | (1) |
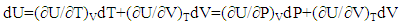 | (2) |
3. Kinetic Energy and Material Energy
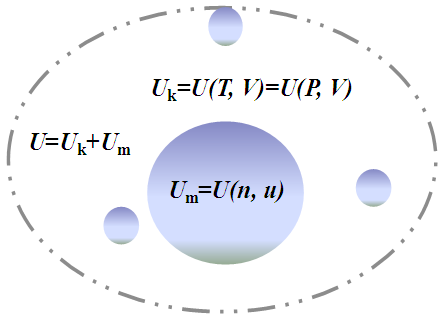
- A molecule possesses an internal energy (or material energy) that is stored inside the molecule (Em). A moving molecule may also have a kinetic energy (Ek) relative to a static system. Therefore, the total energy related to a material consists of two basic energy components, Em and Ek. Using Ei to represent the total amount of energy that can be extracted from material i, we have
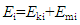 Since a thermodynamic system is a system that contains the materials under study, the total internal energy of the system U should be equal to the sum of energy contributed by all materials contained in the system (Figure 1), namely,
Since a thermodynamic system is a system that contains the materials under study, the total internal energy of the system U should be equal to the sum of energy contributed by all materials contained in the system (Figure 1), namely,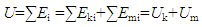 | (3) |
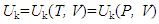 | (4) |
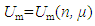 | (5) |
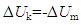 | (6) |
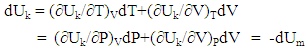 | (7) |
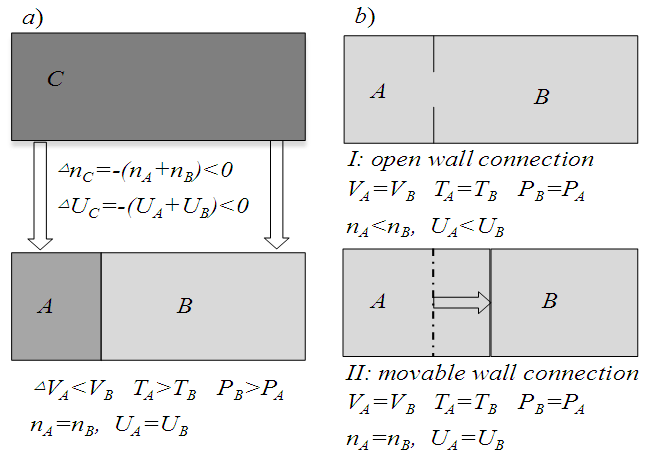
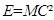 which, since E=0 if M=0, gives support to the idea that energy is matter-dependent. Based on this equation, it would then be impossible to separate energy from matter. There should be no doubt that the exchange of Um between systems is a consequence of matter exchange. The momentum of a particle may be transferred to other particles in the same system by physical attraction or contact. The system will not lose its internal energy because of the particle attraction or contact in the system. The particles of a system do not contribute Uk to its surroundings unless they move out from the system to its surroundings. The concept of traditionally defined closed system infers the presence of such systems that allow energy exchange only. Assuming the presence of ideal empty systems, it would be difficult to imagine how energy could flow into a closed empty system that contained no matter. It is not all materials contained in a system that can be exchanged under natural conditions. Small particles with high mobility can spontaneously move across the boundary between systems. Heavier materials may be held by gravity and remain static in the system. Such materials, if they do not emit heat, have no direct impact on system T and P except for occupying a portion of system space. Heavy materials do not spontaneously undergo matter exchange process unless additional forces are provided. Another important factor for matter exchange is the nature of the system wall. The concepts of open, closed and isolated systems should be linked to the their degrees of openness including permeability and conductivity regarding matter exchanges. Thus, spontaneous energy exchange should depend on two necessary conditions, the mobility of the materials and the degree of openness of the system. The traditionally defined closed systems that allow energy exchange only do not exist in reality.
which, since E=0 if M=0, gives support to the idea that energy is matter-dependent. Based on this equation, it would then be impossible to separate energy from matter. There should be no doubt that the exchange of Um between systems is a consequence of matter exchange. The momentum of a particle may be transferred to other particles in the same system by physical attraction or contact. The system will not lose its internal energy because of the particle attraction or contact in the system. The particles of a system do not contribute Uk to its surroundings unless they move out from the system to its surroundings. The concept of traditionally defined closed system infers the presence of such systems that allow energy exchange only. Assuming the presence of ideal empty systems, it would be difficult to imagine how energy could flow into a closed empty system that contained no matter. It is not all materials contained in a system that can be exchanged under natural conditions. Small particles with high mobility can spontaneously move across the boundary between systems. Heavier materials may be held by gravity and remain static in the system. Such materials, if they do not emit heat, have no direct impact on system T and P except for occupying a portion of system space. Heavy materials do not spontaneously undergo matter exchange process unless additional forces are provided. Another important factor for matter exchange is the nature of the system wall. The concepts of open, closed and isolated systems should be linked to the their degrees of openness including permeability and conductivity regarding matter exchanges. Thus, spontaneous energy exchange should depend on two necessary conditions, the mobility of the materials and the degree of openness of the system. The traditionally defined closed systems that allow energy exchange only do not exist in reality.4. Work and Heat
4.1. Work Linked to the Change in V given P
- Assuming that a work done by a system on its surroundings had led to a decrease in U of the system from Ui to Uf, and that in the process there had been no heat exchange, q=0, from Equation (1), we would have
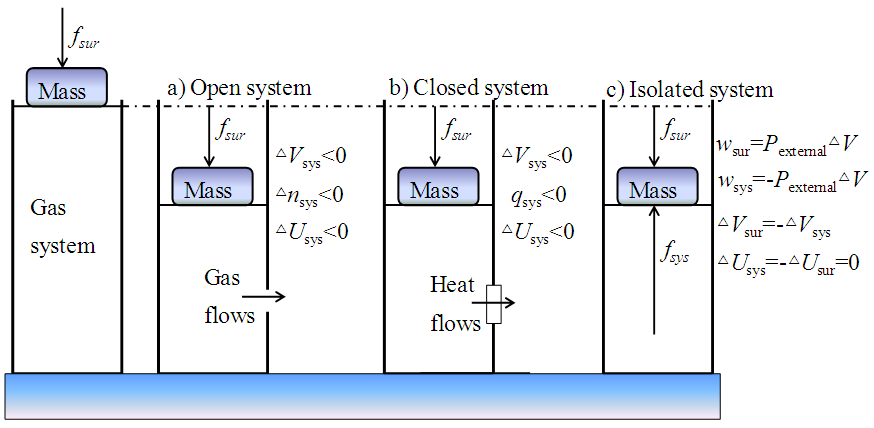
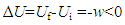 Since ∆U had a fixed value which was equal to Uf minus Ui, the relation ∆U=-w would mean that given q=0, w could also be uniquely determined by the difference between Uf and Ui. Since, however, w is a path-dependent variable which cannot be uniquely determined by the difference between Uf and Ui, the conclusion that ∆U=-w given q=0 may not hold in general. As a path function, the expansion work w is related to the change in V since w=0 if ∆V=0. Like w, the change in V or U is not a system property either because a system does not have a ∆V or ∆U value at a given state. The difference between w and ∆U is that w varies with path conditions while ∆U is always equal to Uf minus Ui no matter how much work has been done in the process. Systems can do work while the work performed may not be equal to the energy consumed. It has been understood that the change in U of a system could only be fully converted to work in reversible processes. If this were true, we would have w<-∆U since all natural processes are irreversible. It has been generally believed that a work done by a system on its surroundings would lead to a decrease in U of the system associated with an equal increase in U of the surroundings, or vice visa. It is known that the performance of a mechanical work involves both acting and reacting forces. As a general rule, whatever the types of forces are, the acting and reacting forces (as vectors) will always be equal, appearing simultaneously but towards opposite directions. Thus in principle, any mechanical work (e.g., an expansion work) done by a system on its surroundings should be equal to the work done by the surroundings on the system. It is impossible to compress a system by a force unless the system is held tightly by a counterforce. Otherwise, the system will obtain an acceleration and move towards the direction of the force. Assume that a gas cylinder held by its gravity on the ground was compressed by an external force, and according to the traditional theory, the system should gain energy, namely ∆Usys>0. If the cylinder was an open system (Figure 2a), the increase in internal P due to the compression would lead to a gas flow out of the system; while if the cylinder was a traditionally defined closed system (Figure 2b), the increase in internal T due to the compression would lead to a heat flow out of the system. In both cases, the consequence would be ∆Usys=-∆Usur<0, meaning that the system would lose rather than gain energy because of the work done by its surroundings. If the cylinder was isolated to prevent matter and heat exchange (Figure 2c), the compression work (wsur) done by the external force should be equal to the work (wsys) done by the internal pressure to resist the compression, namely, wsur=Pexternal∆V=-wsys or wsur+wsys=0. Assuming that the internal energy could be converted to "work flows", the amount of "work flows" flowed from the surroundings into the cylinder would be equal to that from the cylinder to the surroundings. Thus in accordance with the first law of thermodynamics that ∆U =0 in isolated systems, the energy exchange between the cylinder and its surroundings would eventually be zero, namely, ∆Usys=-∆Usur =0. The cases shown in Figure 2 indicate that mechanical work can only cause energy exchange between open and closed systems while the direction of the energy flow is not necessarily determined by the work but by the second law of thermodynamics.
Since ∆U had a fixed value which was equal to Uf minus Ui, the relation ∆U=-w would mean that given q=0, w could also be uniquely determined by the difference between Uf and Ui. Since, however, w is a path-dependent variable which cannot be uniquely determined by the difference between Uf and Ui, the conclusion that ∆U=-w given q=0 may not hold in general. As a path function, the expansion work w is related to the change in V since w=0 if ∆V=0. Like w, the change in V or U is not a system property either because a system does not have a ∆V or ∆U value at a given state. The difference between w and ∆U is that w varies with path conditions while ∆U is always equal to Uf minus Ui no matter how much work has been done in the process. Systems can do work while the work performed may not be equal to the energy consumed. It has been understood that the change in U of a system could only be fully converted to work in reversible processes. If this were true, we would have w<-∆U since all natural processes are irreversible. It has been generally believed that a work done by a system on its surroundings would lead to a decrease in U of the system associated with an equal increase in U of the surroundings, or vice visa. It is known that the performance of a mechanical work involves both acting and reacting forces. As a general rule, whatever the types of forces are, the acting and reacting forces (as vectors) will always be equal, appearing simultaneously but towards opposite directions. Thus in principle, any mechanical work (e.g., an expansion work) done by a system on its surroundings should be equal to the work done by the surroundings on the system. It is impossible to compress a system by a force unless the system is held tightly by a counterforce. Otherwise, the system will obtain an acceleration and move towards the direction of the force. Assume that a gas cylinder held by its gravity on the ground was compressed by an external force, and according to the traditional theory, the system should gain energy, namely ∆Usys>0. If the cylinder was an open system (Figure 2a), the increase in internal P due to the compression would lead to a gas flow out of the system; while if the cylinder was a traditionally defined closed system (Figure 2b), the increase in internal T due to the compression would lead to a heat flow out of the system. In both cases, the consequence would be ∆Usys=-∆Usur<0, meaning that the system would lose rather than gain energy because of the work done by its surroundings. If the cylinder was isolated to prevent matter and heat exchange (Figure 2c), the compression work (wsur) done by the external force should be equal to the work (wsys) done by the internal pressure to resist the compression, namely, wsur=Pexternal∆V=-wsys or wsur+wsys=0. Assuming that the internal energy could be converted to "work flows", the amount of "work flows" flowed from the surroundings into the cylinder would be equal to that from the cylinder to the surroundings. Thus in accordance with the first law of thermodynamics that ∆U =0 in isolated systems, the energy exchange between the cylinder and its surroundings would eventually be zero, namely, ∆Usys=-∆Usur =0. The cases shown in Figure 2 indicate that mechanical work can only cause energy exchange between open and closed systems while the direction of the energy flow is not necessarily determined by the work but by the second law of thermodynamics. 4.2. Heat Related to T Given V or S
- The argument presented here is that all materials and systems have heat states that can be uniquely determined by T given V or S, heat can be exchanged, and heat is thus a state function. Assuming that heat exchange had led to an increase in U of a system from Ui to Uf, from Equation (1) given in the process w=0, we would have
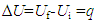 showing that given w=0, the uptake of heat q can be uniquely determined by the difference between Uf and Ui. This, in accordance with the first law of thermodynamics, would lead to a conclusion that if heat exchange did cause changes in U, heat should be a state function related to U. There appears to have no conclusive evidences to indicate that heat is a path function. The unique reasoning on this matter noticed in textbooks [2, 3] was based on the relation ∆U=q-w, saying that because given the initial and final states, ∆U is the same for each path, w can be different for each path, and q has to be different for each path. This conclusion would lack a logic base if ∆U≠q-w. The concept of q is different from that of w. The symbol w denotes the work done by the system while q does not denote the heat but the uptake of heat by or, equivalently, the change in heat state of the system. A system can do but cannot have (or possess) a work. In contrast, a system can either withdraw or release heat, implying that a system can either obtain, or lose, or possess heat. Fuel materials disappear when being burned to generate heat, indicating that heat exchange involves matter exchange. Experiences tell us that heat can be directly transferred by mass transfer or, similar to electricity, by conduction. Like electric current, the conducted heat should also be a current of hot particles. Similar to other radiation activities, heat emission is a matter exchange phenomenon. It is thus puzzled why heat has been treated as a path variable in thermodynamics that deals with thermal phenomena. The quantity of heat withdrawn by a system in a reversible process is given by qr=T∆S. Since S has been proved to be a system property, TS is a state function. As a matter of fact, if in an energy exchange process nothing else but heat exchange takes place, following the law of energy conservation, we should always have q=∆(TS) disregarding the reversibility of the process. The traditionally defined thermal equilibrium is actually determined by the Uk/V ratio, namely, systems A and B reaching thermal equilibrium at TA=TB corresponding to UkA/VA=UkB/VB. This implies that at the equilibrium state, systems A and B can have different Um/V and thus U/V values. Since TS is a function of T determined by Uk/V, from Equation (4), we can establish the connection
showing that given w=0, the uptake of heat q can be uniquely determined by the difference between Uf and Ui. This, in accordance with the first law of thermodynamics, would lead to a conclusion that if heat exchange did cause changes in U, heat should be a state function related to U. There appears to have no conclusive evidences to indicate that heat is a path function. The unique reasoning on this matter noticed in textbooks [2, 3] was based on the relation ∆U=q-w, saying that because given the initial and final states, ∆U is the same for each path, w can be different for each path, and q has to be different for each path. This conclusion would lack a logic base if ∆U≠q-w. The concept of q is different from that of w. The symbol w denotes the work done by the system while q does not denote the heat but the uptake of heat by or, equivalently, the change in heat state of the system. A system can do but cannot have (or possess) a work. In contrast, a system can either withdraw or release heat, implying that a system can either obtain, or lose, or possess heat. Fuel materials disappear when being burned to generate heat, indicating that heat exchange involves matter exchange. Experiences tell us that heat can be directly transferred by mass transfer or, similar to electricity, by conduction. Like electric current, the conducted heat should also be a current of hot particles. Similar to other radiation activities, heat emission is a matter exchange phenomenon. It is thus puzzled why heat has been treated as a path variable in thermodynamics that deals with thermal phenomena. The quantity of heat withdrawn by a system in a reversible process is given by qr=T∆S. Since S has been proved to be a system property, TS is a state function. As a matter of fact, if in an energy exchange process nothing else but heat exchange takes place, following the law of energy conservation, we should always have q=∆(TS) disregarding the reversibility of the process. The traditionally defined thermal equilibrium is actually determined by the Uk/V ratio, namely, systems A and B reaching thermal equilibrium at TA=TB corresponding to UkA/VA=UkB/VB. This implies that at the equilibrium state, systems A and B can have different Um/V and thus U/V values. Since TS is a function of T determined by Uk/V, from Equation (4), we can establish the connection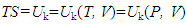 | (8) |
5. Connections with Conventional State Functions
- Equation (8) shows a connection between VP and TS, inferring that the energy term VP is another expression of TS. Before establishing this connection, however, the fact that PV is not a component of the traditionally defined H and A needs to be clarified. From ∆H=∆U+P∆V and ∆A=∆G-P∆V, we see that for systems with rigid walls, ∆V=0, ∆H=∆U and ∆A=∆G, suggesting that PV is, at least, not an essential component of the traditionally defined H and A. Recalling the path conditions for ∆H=qP=∆U+P∆V, we could argue that for a system to expand under a constant pressure condition, energy must be provided from somewhere to do the expansion work. Otherwise, it would violate both the first and second laws. The system withdrawn heat (qP>0) and thus no heat flowed out of the system. Since the system did not get any energy from matter exchange (∆n=0) and nonexpansion work (wnonexpansion=0), the only possibility left for the system to maintain constant P (and thus Uk/V) while expanding would have to use the heat obtained from its surroundings. Then we would have P∆V=qP. Since qP>0, ∆U>0, which should in turn cause changes in the state of at least one of the system properties. In other words, the inputted heat had to be deposited somewhere in the system. Since only V of the system changed, this change had to be an effect of the heat uptake. Note that P∆V>0 and P∆V is an energy term, meaning that the system gained rather than lost energy. In the process the surroundings lost an equal amount of heat, which could be accounted for by its reduced space volume, ∆Usur=-qP=-P∆V. Thus for the system, ∆Usys=∆H=qP=P∆V, implying that the expansion was a consequence of heat uptake. In other words, the system did not lose energy because of the expansion work.Given ∆H=0, the relation H=U+PV=G+TS leads to two seemingly related consequences: ∆U=-∆(PV) and ∆G=-∆(TS). This means that if H remains constant, the change in G will only cause the change in TS while the change in U will be uniquely determined by the change in PV. The consequence ∆U=-∆(PV) can hardly be true since there is no reason why U should decrease with increasing VP. The explanation is simple because ∆H=0 does not satisfy the basal condition for generalizing H, which demands, at least, ∆H=qP≠0. Despite of this, since G is a component of U, and changes in G may lead to changes in U, there had to be a connection between them and the possible link could be ∆(TS)=∆(PV). This link sounds reasonable as it confirms the connection between TS and PV. Given ∆H=0 in isolated systems, however, if ∆(TS)=∆(PV), ∆G=-∆(TS)=0 since ∆U=-∆(VP)=0, while if ∆(TS)=∆(PV)≠0, ∆U≠0 unless ∆U≠∆H-∆(PV). The relation ∆G=-∆(TS) given ∆H=0 defines a specific condition under which the change in G can be fully converted to that in TS in the system, implying that the change in G causes no changes in U. In other words, the precondition for ∆G=-∆(TS) is ∆U=0, meaning that ∆H=0 is a synonym of ∆U=0. Then, giving ∆H=0, ∆U=0, ∆G=-∆(TS) and ∆A=∆U-∆(TS)=-∆(TS)=∆G.The connection between P and T given by the empirical relation (or the ideal gas law) [1-3] is VP=nRT, where R is the gas constant. The ideal gas law gives a logical support to the connection between PV and TS. The total system volume V is equal to the space unoccupied by materials Vk plus that occupied by materials Vm. Let Vk/V+Vm/V=δ+(1-δ), which gives Vk=δV. We can argue that it should be VkP rather than VP that is proportional to nRT, namely,
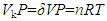 which suggests that the empirical relation VP=nRT may only hold at δ≈1 and Vk≈V when n approaches zero. This can be a logical explanation to the observed phenomena that the ideal gas law did not work satisfactorily at high P due to increasing n. Based on Equation (8), for unifying the unit, we can use a proportional factor k to connect δVP and TS,
which suggests that the empirical relation VP=nRT may only hold at δ≈1 and Vk≈V when n approaches zero. This can be a logical explanation to the observed phenomena that the ideal gas law did not work satisfactorily at high P due to increasing n. Based on Equation (8), for unifying the unit, we can use a proportional factor k to connect δVP and TS,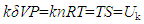 | (9) |
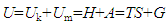 | (10) |
6. Conclusions
- The relation U=TS+G may be considered the simplest expression of U at the highest macroscopic level. Depending on the interest of study, both G and TS can be divided into detailed portions in accordance with the nature of materials and systems. It is necessary to mention that the present work agrees with the existing laws and experimental findings except for presenting different interpretations of the internal energy functions. The following conclusions can be drawn from the above discussions:(1) The total internal energy U consists of two basic components, Uk, the total kinetic energy of the material particles moving in the interior space of the system, and Um, the total internal energy stored in other forms inside the materials contained by the system. (2) Energy is matter-dependent and energy exchange is a process of matter exchange.(3) Work as a path function is not quantitatively related to ∆U. (4) Heat is a state function that can be determined by T given V or S. (5) Components Uk and Um are connected to H, S, A and G as Uk=TS=H and Um=A=G.
ACKNOWLEDGMENTS
- The present study forms part of the projects (2012GS430203, 2014BAC09B00) supported by the Ministry of Science and Technology, China, and the Educational Department of Hunan Province (the Key Subject and Lab).
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML