-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Physical Chemistry
p-ISSN: 2167-7042 e-ISSN: 2167-7069
2012; 2(6): 100-102
doi: 10.5923/j.pc.20120206.03
The Significance and the Basis for the Taft ρ* Value: A One Hour Physical-Organic Chemistry Classroom Lecture to Graduate Students
1Department of Chemistry, Osmania University, Hyderabad, 500007, India
2Department of Chemistry, Mizan-Tepi University, Tepi Campus, Tepi, Ethiopia
Correspondence to: V. Jagannadham, Department of Chemistry, Osmania University, Hyderabad, 500007, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The effect of substituents either in meta or in para position in the benzene ring on the rate or equilibrium constant is given by Hammett in the form of an equation: log K = log Ko + ρσ or log k = log ko + ρσ respectively. Where K is the equilibrium constant of the substituted reactant and Ko is that of un-substituted reactant and k is the rate constant of the substituted reactant and ko is that of un-substituted reactant. ρ is the reaction constant and σ is the substituent constant. From the experimental data of several compounds for the values of K and Ko, and choosing an arbitrary value of one for ρ at 25oC, Hammett computed σ values for several meta and para substituents in benzene derivatives. However the Hammett equation failed to explain the structural effects in ortho-substituted benzene derivatives and aliphatic systems. Subsequently Taft formulated an equation, 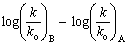 = ρ*σ*, on the basis of the same grounds of Hammett equation, but using the data on acid and base catalysed hydrolysis of esters. Here k and ko are the rate constants of substituted ester and that of ethyl acetate respectively and the suffixes A and B stand for acid and base catalysis. Taft has taken a value of 2.48 for ρ* that is analogous to the value of one for ρ in the Hammett equation. The basis and significance for the value of 2.48 in the above rearranged equation
= ρ*σ*, on the basis of the same grounds of Hammett equation, but using the data on acid and base catalysed hydrolysis of esters. Here k and ko are the rate constants of substituted ester and that of ethyl acetate respectively and the suffixes A and B stand for acid and base catalysis. Taft has taken a value of 2.48 for ρ* that is analogous to the value of one for ρ in the Hammett equation. The basis and significance for the value of 2.48 in the above rearranged equation 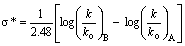 to Taft ρ*was given in this article. This is a very useful lecture for graduate students who are interested in learning structure-reactivity correlations and reaction mechanisms.
to Taft ρ*was given in this article. This is a very useful lecture for graduate students who are interested in learning structure-reactivity correlations and reaction mechanisms.
Keywords: Taft Equation, Taft ρ*Value
Cite this paper: V. Jagannadham, R. Sanjeev, "The Significance and the Basis for the Taft ρ* Value: A One Hour Physical-Organic Chemistry Classroom Lecture to Graduate Students", Physical Chemistry, Vol. 2 No. 6, 2012, pp. 100-102. doi: 10.5923/j.pc.20120206.03.
Article Outline
1. Introduction
- Taft equation is often employed in biological chemistry and medicinal chemistry for the development of quantitative structure activity relationships (QSAR)[1]. In a recent example, Sandri and co-workers have used Taft plots to study the polar effects in the aminolysis of β-lactams. It was seen that at the binding site of β-lactams to a poly(ethyleneimine) polymer, which mimics human serum albumin (HSA). The formation of a covalent bond between penicillin derivatives and HSA as a result of aminolysis with lysine residues is believed to be involved in penicillin allergies. The non-linearity of the rates of aminolysis versus calculated σ* values for 6 penicillin derivatives led them to conclude that the rates are influenced by other effects in addition to polar and steric effects. The putative Hammett equation, log (K/Ko) = ρσ is useful to explain the effect of structure on reactivity in meta and para substituted benzene derivatives. Using this equation, to evaluate the σ values of various substituents, Hammett assumed a value of 1.00 for ρ at 25o C in aqueous solution for the dissociation equilibriums of benzoic acids[2]. Similarly the Taft equation, log (k/ko)B - log (k/ko)A = σ*ρ* was useful to explain the effect of structure on reactivity in aliphatic and ortho substituted benzene derivatives. Here the ρ* was not simply given a value of 1.00 as in the case of Hammett equation, but it was given 2.48. The significance and the basis for this value are discussed in this article.
2. Objectives
- The basis and significance for the value of 2.48 in the equation
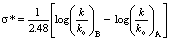 to Taft ρ* was given in this article. This is a very useful lecture for graduate students who are interested in learning structure-reactivity correlations and reaction mechanisms.
to Taft ρ* was given in this article. This is a very useful lecture for graduate students who are interested in learning structure-reactivity correlations and reaction mechanisms.3. Methods
- The essential core background of Hammett equation and its failure of the application to ortho-substituted benzene derivatives and to aliphatic systems are successfully used in this article.
4. Discussion
- The emergence of Taft equation is a consequence of failure of the Hammett equation when the logarithms of the rates of hydrolysis of substituted aliphatic esters are plotted against the pKa values of the corresponding acids. This is an indication of no relationship between the effects of substituents on rates of ester hydrolysis. A similar situation was also found in the case of ortho-substituted aromatic substrates. This leads to a conclusion that the absence of proximity effects is no longer valid. Yet the linear free energy relationships may still be observed with some restrictions which may be placed upon the type of reactions taking place. Thus the BrØnsted equation may be applied if the changes are in a limited class of acid- and base-catalysed reactions. Reasonably good trends in the acid strengths were seen on several occasions. It is largely the data on ester hydrolysis is accountable for failure of simple correlations. Following a suggestion by Ingold[3], Taft arrived at polar substituent constants in aliphatic series by studying the reactions where the resonance effects are constant (R) as in the case of base- and acid- catalysed hydrolysis of aliphatic esters for which ethyl acetate reaction is taken as standard. It is clear that base-catalysed reactions show a very remarkable response to substituent polar effects (P) because reactant goes from a neutral species to negatively charged intermediate in the rate determining (slow) step as shown in scheme 1:
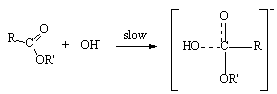 | Scheme 1. Rate determining attack of base on the ester |
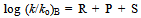 | (1) |
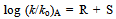 | (2) |
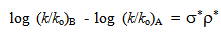 | (3) |
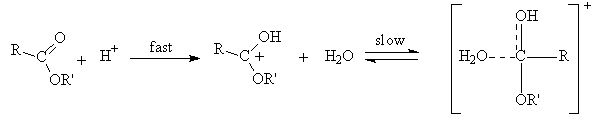 | Scheme 2. Acid catalysed hydrolysis of ester with rate determining attack of water |
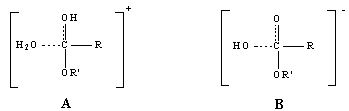 | Scheme 3. Tetrahedral intermediates in acid (A) and base (B) catalysed hydrolysis of ester |
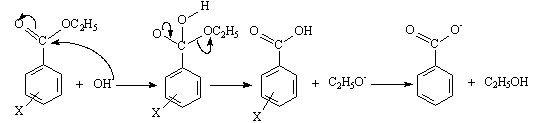 | Scheme 4. Base catalysed hydrolysis of meta- and para-substituted ethyl benzoates |
5. Basis for the Taft ρ*
- Now the question is to evaluate σ* values using equation 3. For this yet one should know the value of ρ* as the rate constants k, and ko are experimentally determinable. As in the case of Hammett equation it was easy to evaluate Hammett σ values because, Hammett has simply assumed ρ as 1.0 for the dissociation equilibriums of benzoic acids in aqueous solution at 25oC. But Taft did not simply use 1.0 as ρ*. In an attempt to place the σ* values on the same scale as the Hammett σ values, ρ* value for alkyl ester hydrolysis was set equal to 2.48 and not to 1.00. Why did Taft use 2.48? It could have been 0.50 or 1.00 or 1.50 or 2.00 or 2.50 or 3.00 or any other value. From our teaching experience of physical-organic chemistry for the last 35-40 years to undergraduate and graduate students, we understand this particular aspect of mechanistic application of Taft equation is either ignored or not appropriately stressed while teaching applications of Taft equation in a physical-organic chemistry graduate class-room. In fact the value 2.48 is the mean values of the Hammett reaction constants[3b, 4] ρB for base-catalysed hydrolysis (BAc2 mechanism: bimolecular, base catalysed, acyl oxygen fission) of meta and para- substituted ethyl and methyl benzoates (scheme 4) in different solvents and at different temperatures.With this ρ* value, and with experimentally determined average values of log (k/ko)B for several alkyl groups and solvent compositions the following equation becomes the definition of the σ* values.
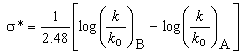
6. Conclusions
- The confusion among both the teachers and students in understanding the significance of the value of ρ* is equal to 2.48 is clarified in a lucid way in general and to the physical-organic chemistry class-room graduate students in particular.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML