-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Physical Chemistry
p-ISSN: 2167-7042 e-ISSN: 2167-7069
2012; 2(5): 80-85
doi: 10.5923/j.pc.20120205.04
A New Theoretical Study of Desorption Kinetics at Solid/Solution Interface by Statistical Rate Theory
Hadis Bashiri
Department of Physical Chemistry, Faculty of Chemistry, University of Kashan, Kashan, 87317-51167, Iran
Correspondence to: Hadis Bashiri , Department of Physical Chemistry, Faculty of Chemistry, University of Kashan, Kashan, 87317-51167, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Desorption is one of the popular methods for the design and regeneration of catalysts. For better understanding and modeling of this process, it is important to have models with theoretical basis. In the present work kinetics of solute desorption at solid/solution interface has been studied by statistical rate theory (SRT) when the system is close to equilibrium. Based on numerically generated points (t; q) by the SRT equation, it has been shown that the results of numerical analysis are in good agreement with our theoretical derivation of new rate equation for desorption systems close to equilibrium. Finally the results of the present theoretical study were confirmed by analysis of two experimental systems.
Keywords: Desorption Kinetics, Solid/Solution Interface, Statistical Rate Theory, Rate Equation
Cite this paper: Hadis Bashiri , "A New Theoretical Study of Desorption Kinetics at Solid/Solution Interface by Statistical Rate Theory", Physical Chemistry, Vol. 2 No. 5, 2012, pp. 80-85. doi: 10.5923/j.pc.20120205.04.
1. Introduction
- Adsorption and desorption processes are the most popular methods for removal of pollutants from wastewaters[1-3]. Sometimes for contaminants separation process, adsorption method is used firstly and then to release of adsorbed species, desorption process is needed[4, 5]. Therefore desorption kinetic and equilibrium are important in understanding desorption characteristics from adsorbent. Kinetic of desorption has been studied extensively, experimentally and theoretically. Kinetic equations commonly are used in desorption studies including zero order[6], pseudo first order[7, 8], pseudo second order[7, 8], and simple Elovich equation[9]. The mentioned models of desorption kinetics were presented experimentally and there are no theoretical interpretation for them. By applying the SRT approach, pseudo first order kinetic model has been derived for desorption at the solid/solution interface[10].Statistical rate theory (SRT) approach has been used for modeling of desorption kinetics at gas/solid[11, 12] and solid/solution interfaces[13]. The analytical solution of the basic equation of SRT for kinetics of desorption at solid/solution interface led to a complex expression. Recently, we have derived simple equations for description of desorption kinetics at limiting conditions[10, 13]. This article is intented to derive a desorption rate equation on the basis of statistical rate theory at close to equilibrium condition.
2. Theory Section
- The statistical rate theory (SRT) approach, which is based on quantum mechanics and thermodynamics, has been provided by Ward[14, 15]. Rudzinski et al has shown how the SRT approach can further be generalized to describe the kinetic of adsorption at gas/solid[16, 17] and solid/solution[18, 19] interfaces. Recently, we have used the SRT approach for adsorption kinetics near the initial times of adsorption and close to equilibrium[20] and also for description of competitive adsorption at solid/solution interface[21].The general rate expression to describe the kinetics of adsorption is presented by the following form[17, 18]
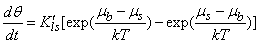 | (1) |
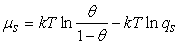 | (2) |
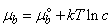 | (3) |
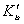 [20]
[20]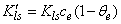 | (4) |
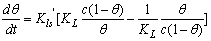 | (5) |
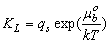 | (6) |
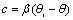 | (7) |
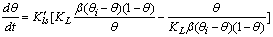 | (8) |
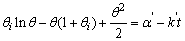 | (9) |
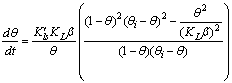 | (10) |
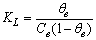 ). On the basis of eq 7, the equilibrium bulk concentration (ce) in Langmuir isotherm is equal to
). On the basis of eq 7, the equilibrium bulk concentration (ce) in Langmuir isotherm is equal to 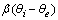 , so
, so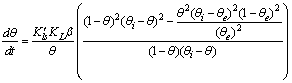 | (11) |
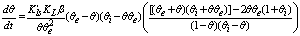 | (12) |
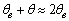 ,
, 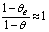 and
and 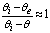 in eq 12 are acceptable. Based on these assumptions eq 12 simplifies to
in eq 12 are acceptable. Based on these assumptions eq 12 simplifies to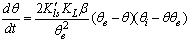 | (13) |
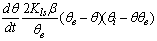 | (14) |
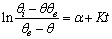 | (15) |
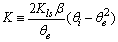 | (16) |
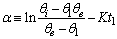 | (17) |
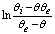 is a linear function of time (for
is a linear function of time (for 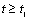 ). The intercept of this plot is α and the tangent is K. In the next section by using generated and experimental data the accuracy of present derivations will be discussed.
). The intercept of this plot is α and the tangent is K. In the next section by using generated and experimental data the accuracy of present derivations will be discussed.3. Results and Discussion
- In this section, we are going to analyse the applicability of the derived equation (eq 15). The analytical solution of eq 8 led to a complex expression. One powerful technique for numerical simulations is stochastic simulation. For this purpose three sets of hypothetical kinetic data points (q; t) were generated based on SRT rate equation for desorption at solid/solution interface (eq 8). For this purpose we applied the CKS package developed by Houle and Hinsberg[23,24]. Recently we utilized this method for numerical solution of some adsorption and desorption kinetic equations, successfully[10,13,20]. For simplification of eq 8 the adsorption and desorption rate constants (ka and kd) are defined as
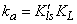 | (18) |
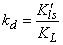 | (19) |
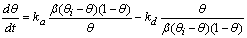 | (20) |
| |||||||||||||||||||||||||||||||||||||||||
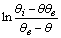 as a function of time were calculated for close to equilibrium data (see eq 15) and plotted in Figure 1(b). The value of θe was adjusted until the intercept of the linear plot became equal to α (eq 17). The adjustable value of θe is reported in Table 2. By utilizing the slope of Figure 1(b) (K constant), the value of Kls was calculated by eq 16 and was reported in Table 2. The Kls value was obtained from the SRT rate equation by eqs 4, 18 and 20 and is reported in Table 2. Agreement between the obtained Kls values from the SRT rate equation and from eq 15, confirms the accuracy of new derived equation.
as a function of time were calculated for close to equilibrium data (see eq 15) and plotted in Figure 1(b). The value of θe was adjusted until the intercept of the linear plot became equal to α (eq 17). The adjustable value of θe is reported in Table 2. By utilizing the slope of Figure 1(b) (K constant), the value of Kls was calculated by eq 16 and was reported in Table 2. The Kls value was obtained from the SRT rate equation by eqs 4, 18 and 20 and is reported in Table 2. Agreement between the obtained Kls values from the SRT rate equation and from eq 15, confirms the accuracy of new derived equation.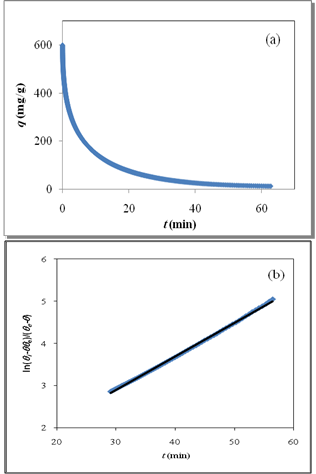 | Figure 1. (a) Numerically generated data points (t; q) based on SRT equation for ka =1.00×10-5 min-1 and kd =1.00×10-5 mol2/L2.min. (b) Linear plot of eq 15 when system is close to equilibrium |
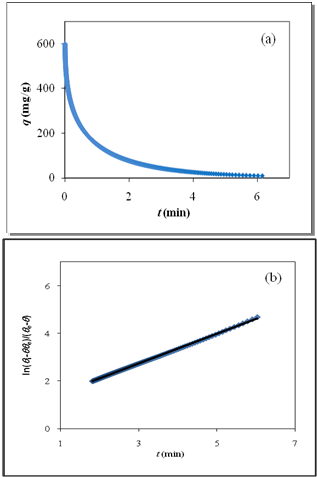 | Figure 2. (a) Numerically generated data points (t; q) based on SRT equation for ka =1.00×10-5 min-1 and kd =1.00×10-4 mol2/L2.min, (b) Linear plot of eq 15 when system is close to equilibrium |
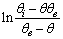 vs time for close to equilibrium desorption kinetic data (Figure 2(b) and Figure 3(b)). The values of θe were obtained as adjustable parameters and are listed in Table 2. The Kls values calculated from these results are listed in Table 2. The comparison between the obtained Kls values and the original ones (calculated by SRT rate equation) proves the accuracy of the above derivation again.
vs time for close to equilibrium desorption kinetic data (Figure 2(b) and Figure 3(b)). The values of θe were obtained as adjustable parameters and are listed in Table 2. The Kls values calculated from these results are listed in Table 2. The comparison between the obtained Kls values and the original ones (calculated by SRT rate equation) proves the accuracy of the above derivation again.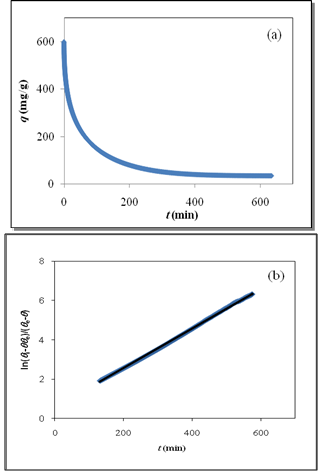 | Figure 3. (a) Numerically generated points (t; q) based on SRT equation for ka =1.00×10-5 min-1 and kd =1.00×10-6 mol2/L2.min, (b) linear plot of eq 15 when the system is close to equilibrium |
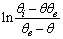 as a function of time were plotted for desorption kinetic data close to equilibrium (Figure 4(b)), the Kls and θe values were obtained and are listed in Table 2. The obtained values of Kls are close to the original ones (Kls obtained from SRT rate equation). The obtained results of these experimental data prove the accuracy of our derivation for desorption rate equation.
as a function of time were plotted for desorption kinetic data close to equilibrium (Figure 4(b)), the Kls and θe values were obtained and are listed in Table 2. The obtained values of Kls are close to the original ones (Kls obtained from SRT rate equation). The obtained results of these experimental data prove the accuracy of our derivation for desorption rate equation.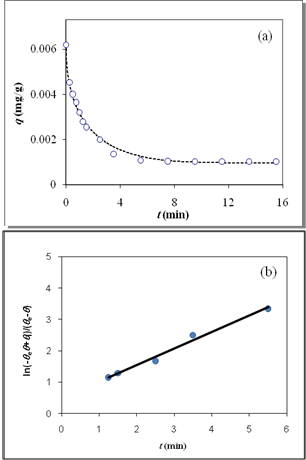 | Figure 4. (a) Desorption kinetics of vitamin E from silica, experimental data (open circles)25 and theoretical data based on SRT equation (solid line), (b) Linear plot of eq 15 when the system is close to equilibrium |
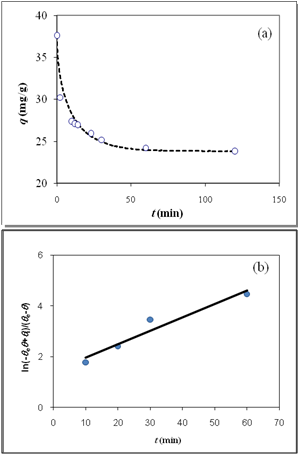 | Figure 5. (a) Desorption kinetics of Cadmium(II) from Aeromonas caviae, experimental data (open circles)26 and theoretical data based on SRT equation (solid line), (b) Linear plot of eq 15 when the system is close to equilibrium |
4. Conclusions
- The desorption kinetics at the solid/solution interfaces has been studied based on SRT approach at close to equilibrium condition. By considering some assumptions on SRT rate equation, a new rate equation was derived for desorption at solid/solution interface when system is close to equilibrium. Three different sets of numerical desorption kinetic data (q; t) were generated by using SRT rate equation. By utilizing these generated data, the accuracy of the new derived rate equation (eq 15) has been proved. On the basis of two experimental kinetic data, it was indicated that eq 15 can be used for modeling of desorption kinetic data when system is close to equilibrium. Both experimental and generated data were in good agreement with our derivation. For modeling of desorption kinetics based on SRT approach, but by simple equations, one have to use eq 9 for initial times of desorption and eq 15 for near to equilibrium conditions.
References
| [1] | Y. Yin, H.E. Allen, C.P. Huang, D.L. Sparks and P.F. Sanders, “Kinetics of mercury(II) adsorption and desorption on soil”, ACS, Environ. Sci. Technol., vol. 31, pp. 496 -503, 1997. |
| [2] | Y.S. HO and G. McKay, “Batch lead(II) removal from aqueous solution by peat: Equilibrium and Kinetics”, Institution of Chemical Engineers, Trans. IchemE Part B, vol. 77, pp. 165-173, 1999. |
| [3] | Z. Reddad, C. Gerente, Y. Andres and P.L. Cloirec, “Adsorption of several metal ions onto a low-cost biosorbent: kinetic and equilibrium studies”, ACS, Environ. Sci. Technol., vol. 36, pp. 2067-2073, 2002. |
| [4] | D. Chatzopoulos, A. Varma and R.L Irvine, “Activated carbon adsorption and desorption of toluene in the aqueous phase”, Wiley, AIChE J., vol. 39, pp. 2027-2041, 1993. |
| [5] | A. Karimi-Jashni and R.M. Narbaitz, “Impact of pH on the adsorption and desorption kinetics of 2-nitrophenol on activated carbons”, Elsevier, Water Res., vol. 31, pp. 3039-3044, 1997. |
| [6] | A. Reyhanitabar and N. Karimian, “Kinetics of copper desorption of selected calcareous soils from Iran”, IDOSI, Am-Euras. J. Agric. & Environ. Sci., vol. 4, pp. 287-293, 2008. |
| [7] | Y. S. Ho, J. C. Y. Ng and G. McKay, “Kinetics of pollutant sorption by biosorbents: review“, Taylor & Francis, Sep. Purif. Methods, vol. 29, pp. 189-232, 2000. |
| [8] | Z. Li, “Sorption kinetics of hexadecyltrimethylammonium on natural clinoptilolite”, ACS, Langmuir, vol. 15, pp. 6438-6445, 1999. |
| [9] | S.H. Chien and W.R. Clayton, “Application of elovich equation to the kinetics of phosphate release and sorption in soils”, SSSA, Soil Sci. Soc. Am. J., vol. 44, pp. 265-268, 1980. |
| [10] | H. Bashiri, "Desorption kinetics at the solid/solution interface: A theoretical description by statistical rate theory for close-to-equilibrium systems", ACS, J. Phys. Chem. C, vol. 115, pp. 5732-5739, 2011. |
| [11] | W. Rudzinski, T. Borowiecki, T. Panczyk, A. Dominko and W. Gac, "Thermodesorption studies of energetic properties of nickel and nickel-molybdenum catalysts based on the statistical rate theory of interfacial transport", Elsevier, Applied Catalysis A: General, vol. 224, pp. 299-310, 2002. |
| [12] | T. Panczyk, W. Gac, M. Panczyk, T. Borowiecki and W. Rudzinski, "On the equilibrium nature of thermodesorption processes. TPD-NH3 studies of surface acidity of Ni/MgO-Al2O3 catalysts", ACS, Langmuir, vol. 22, pp. 6613-6621, 2006. |
| [13] | S. Azizian and H. Bashiri, " Description of desorption kinetics at the solid/solution interface based on the statistical rate theory", ACS, Langmuir, vol. 24, pp. 13013-13018, 2008. |
| [14] | C. A. Ward, “The rate of gas absorption at a liquid interface“, AIP, J. Chem. Phys., vol. 67, pp. 229-235, 1977. |
| [15] | C. A. Ward, R. D. Findlay and M. Rizk, “Statistical rate theory of interfacial transport. I. theoretical development”, AIP, J. Chem. Phys., vol. 76, pp. 5599-5605, 1982. |
| [16] | W. Rudzinski and T. Panczyk, " Kinetics of isothermal adsorption on energetically heterogeneous solid surfaces: a new theoretical description based on the statistical rate rheory of interfacial transport", ACS, J. Phys. Chem. B, vol. 104, pp. 9149-9162, 2000. |
| [17] | T. Panczyk and W. Rudzinski, "A statistical rate theory approach to kinetics of dissociative gas adsorption on solids", ACS, J. Phys. Chem. B, vol. 108, pp. 2898-2909, 2004. |
| [18] | W. Rudzinski and W. Plazinski, " Kinetics of solute adsorption at solid/solution interfaces: A theoretical development of the empirical pseudo-first and pseudo-second order kinetic rate equations, based on applying the statistical rate theory of interfacial transport", ACS, J. Phys. Chem. B, vol. 110, pp. 16514-16525, 2006. |
| [19] | W. Rudzinski and W. Plazinski, "Application of the statistical rate theory of interfacial transport to investigate the kinetics of divalent metal ion adsorption onto the energetically heterogeneous surfaces of oxides and activated carbons", Elsevier, Appli. Surf. Sci., vol. 253, pp. 5814-5817, 2007. |
| [20] | S. Azizian and H. Bashiri, "Adsorption kinetics at the solid/solution interface: statistical rate theory at initial times of adsorption and close to equilibrium", ACS, Langmuir, vol. 24, pp. 11669-11676, 2008. |
| [21] | S. Azizian, H. Bashiri and H. Iloukhani, "Statistical rate theory approach to kinetics of competitive adsorption at the solid/solution interface", ACS, J. Phys. Chem. C, vol. 112, 10251-10255, 2008. |
| [22] | W. Rudzinski and W. Plazinski, "Theoretical description of the kinetics of solute adsorption at heterogeneous solid/solution interfaces, On the possibility of distinguishing between the diffusional and the surface reaction kinetics models", Elsevier, Appli. Surf. Sci., vol. 253, pp. 5827-5840, 2007. |
| [23] | F. A. Houle and W. D. Hinsberg, “Stochastic simulations of temperature programmed desorption kinetics“, Elsevier, Surf. Sci., vol. 338, pp. 329-346, 1995. |
| [24] | F. A. Houle, W. D. Hinsberg and M. I. Sanches, “Kinetic model for positive tone resist dissolution and roughening”, ACS, Macromolecules, vol. 35, pp. 8591-8600, 2002. |
| [25] | B.S. Chu, B.S. Baharin, Y.B. Cheman and S.Y Queck, “Separation of vitamin E from palm fatty acid distillate using silica. III. Batch desorption study”, Elsevier, J. Food Eng., vol. 64, pp. 1-7, 2004. |
| [26] | M.X. Loukidou, T.D. Karapantsios, A.I. Zouboulis and K.A. Matis, “Diffusion kinetic study of cadmium(II) biosorption by Aeromonas caviae”, SCI, J. Chem. Technol. Biotechnol., vol. 79, pp. 711-719, 2004. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML