Ghazi F. Najmuldeen1, Ghassan Jasim Hadi2, Arkan Jasim Hadi1, Iqbal Ahmed1
1Faculty of Chemical engineering and Natural Resource, University Malaysia Pahang, Kuantan, 26300, Malaysia
2Al Dour Technical Institution, Technical Education Organization, Tikrit, 43200, Iraq
Correspondence to: Arkan Jasim Hadi, Faculty of Chemical engineering and Natural Resource, University Malaysia Pahang, Kuantan, 26300, Malaysia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this work, a thermodynamic model for the prediction of gas-liquid equilibrium at moderate pressures (up to 6 bar) and different temperatures (288-323 K) for the ternary system of carbon dioxide (1)-(2) mixture (ethanol-water) is established using Soave/Redlich/Kwong equation of state (SRK-EOS). Two different mixing rules were used to show the effect of the type of mixing rule. A comparison of experimental phase equilibrium data in the literature with the predicted results showed very good representation for one mixing rule and good for the other.
Keywords:
Gas-Liquid Equilibrium, Moderate Pressure, Mixing Rules, SRK-EOS
Cite this paper: Ghazi F. Najmuldeen, Ghassan Jasim Hadi, Arkan Jasim Hadi, Iqbal Ahmed, Gas-Liquid Equilibrium Prediction of Ternary System (CO2-Ethanol-Water) at Moderate Pressures and Different Temperatures Using SRK-EOS, Physical Chemistry, Vol. 2 No. 1, 2012, pp. 1-5. doi: 10.5923/j.pc.20120201.01.
1. Introduction
The solubility of gases in liquids has been under intense investigation over the past three decades since the knowledge of gas solubility data in pure liquids and in mixed solvents which plays an important role in several industrial processes, such as the carbonation of alcoholic beverages and soft drinks, gas absorption, stripping columns, wastewater treatment, etc.From theoretical point of view, the solubility of gases in liquids, especially in the dilute region, is also a matter of great interest. Experimental solubility data can be used to test molecular theories. It is also used to elucidate intermolecular interactions and microscopic structure[1]. According to Wilhelm et al.[2]. The advantages of low-pressure gas solubility over high-pressure equilibrium data relies on the fact that inaccuracies introduced by possible necessary semi-empirical relations (for example, for the partial molar volume of solute at infinite dilution in the solvent) have essentially no effects on the final results and the thermodynamic treatment is much facilitated by well-defined assumptions[1]. Accurate thermodynamic data such as volumetric properties and phase equilibria of pure compounds and mixtures (i.e.CO2 + alkanes, CO2 + alkanols) are of great significance in the chemical, oil and biotechnology areas, and for the development and validation of thermodynamic models. In this context, it is especially important to know the global phase behavior of systems within the range of working pressures and temperatures[3]. Dalmolin et al.[1]. Were studied the gas solubility data and Henry’s constants for carbon dioxide in pure water and ethanol and in their mixtures. The experiments were performed in the temperature range of 288–323 K, up to 6 atm in pure solvents and at various ethanol–water mixture compositions. Equilibrium measurements for the CO2 + 1-propanol system were performed from 344 to 426 K were studied by Elizalde-Solis et al.[3]. For the case of the CO2 + 2-propanol system, measurements were made from 334 to 443 K, and for the CO2 + 1-butanol were obtained from 354 to 430K. MinqiangHou et al[4]. Studied the solubility of CO2 in polyethylene glycol200 (PEG200, PEG with an average molecular weight of 200 g/ mol), 1-pentanol, and1-octanol.The solubility of thiophene in CO2 and in CO2 + 1-propanol mixtures, were measured by Elizalde and Galicia-Luna [5]. Vapor–liquid equilibria (VLE) data of binary mixtures were fitted to the Peng–Robinson equation of state (EOS) with classical mixing rules. Theoretical results are found by comparing theoretical and experimental data.The results for SRK-EOS for CO2(1)-mixture (2) (ethanol-water) at moderate pressure and different temperature is compared with the experimental data obtained by Dalmolin, et al.[1]
2. Equation of State
Cubic equations of state in fact is the simplest equation capable of representing both liquid and vaporbehavior, it must encompass a wide range of temperature and pressures.Yet it must be not complex to present excessive numerical or an analytical difficulties in application [6]. The general form of SRK-EOS is shown in Table 1.Table 1. General form for SRK-EOS
 |
| |
|
Replacing ν in the general form of SRK-EOS in term of ZRT/P, gives the cubic equation of compressibility factor as shown in Table 2.Table 2. Cubic equation of compressibility factor for SRK-EOS [8]
 |
| |
|
Where Z is the compressibility factor of the liquid mixture and may be calculated from the cubic equation by an iteration method such as Newton-Raphson method.The useful relation for finding fugacity coefficients[8] is,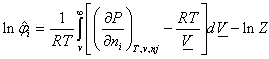 | (1) |
When the SRK-EOSis introduced into Eq. (1), closed-form for fugacity coefficient is obtained in the liquid phase, as in Eq. 2 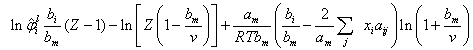 | (2) |
The fugacity coefficients of the components in the gas phase are also calculated with Eq.2 with, yi and all the (SRK) a and b values for the gas replacing their corresponding terms. Most of simple equations of state are evolved from the van der Waal's mixing rules with or without modifications and the mixing rules for equation of state calculate the mixture parameters am and bm for the equation of state according to the one-fluid mixing rules (Eqs. 3 and 4) and the only difference between them is the combining rule that determines how the cross coefficients aij and bij are calculated[6-8].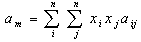 | (3) |
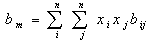 | (4) |
The mixing rules used in this investigation are listed in Table 3.
3. Results and Discussion.
Theoretical solubility of CO2 in mixture is calculated using SRK-EOS with different mixing rules. Calculations included the mole fraction of CO2 in liquid phase (x). The obtained dada from the model are compared with experimental data obtained by Dalmolin, et al.[1]. Critical temperature (Tcm), critical pressure (Pcm) and the acentric factor (ωm) for the mixture (ethanol- water) are calculated by the equations 6, 7 and 8 respectively [10]: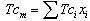 | (6) |
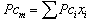 | (7) |
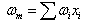 | (8) |
where, Tcm, Pcm, 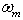 are the critical temperature, critical pressure and acentric factor for mixture. Tci, Pci,
are the critical temperature, critical pressure and acentric factor for mixture. Tci, Pci, 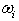 are the critical temperature and critical pressure and acentric factor for ethanol and water.xi , mole fraction of ethanol and water.Adjustable parameter (kij) is obtained from fitting experimental data using SRK-EOS. Additionally the adjustable parameter (Lij) which is used in MR2 is found by trial and error. The calculated parameter which is gives a good results, is shown in Table 4.
are the critical temperature and critical pressure and acentric factor for ethanol and water.xi , mole fraction of ethanol and water.Adjustable parameter (kij) is obtained from fitting experimental data using SRK-EOS. Additionally the adjustable parameter (Lij) which is used in MR2 is found by trial and error. The calculated parameter which is gives a good results, is shown in Table 4.Table 3. List of mixing rules equations used
 |
| |
|
Table 4. Values of Adjustable Parameters Obtained from Fitting with SRK-EOS
 |
| |
|
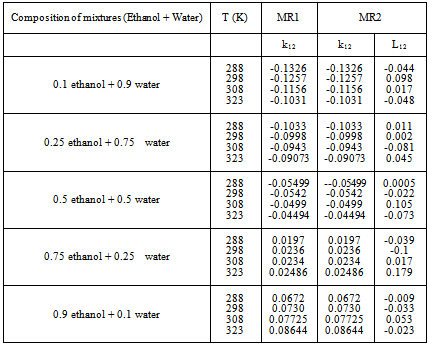
Table 5. MAD between the experimental and predicted mole fraction solubility of CO2 in mixture (Ethanol + Water) with MR1 and MR2 Using SRK
 |
| |
|
The adjustable parameter k12,for the mixture composition (0.1 ethanol+0.9 water) to the composition (0.5 ethanol+0.5 water) was decreases with increasing the temperature, but in the composition (0.75 ethanol+0.25 water) and the composition (0.9 ethanol+0.1 water), k12 increase with increase the temperature note that the increment is very slight compare with the increases of the temperature in this system.Additionally the adjustable parameter L12, indicate vacillation value for the SRK-EOSAn acceptable value of (kij, Lij) which is gives minimum mean absolute deviation (%MAD) is calculated by the Eq. (9)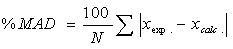 | (9) |
Where, N is the number of data points. Table 5 are shows the %MAD between the Experimental and Predicted mole fraction of CO2 in mixture (Ethanol + Water) with using SRK-EOSThe results from the comparison between the experimental data from literature and the results from the model are shown graphically in Figures (1-8).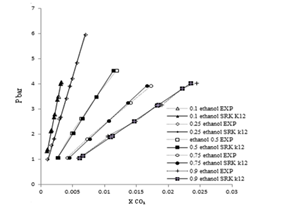 | Figure 1. Phase composition diagram of CO2- Mixture system at 288 K using SRK with MR1 |
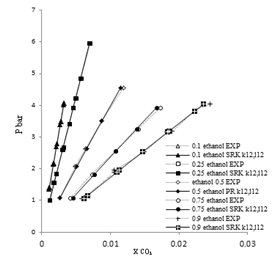 | Figure 2. Phase composition diagram of CO2- Mixture system at 288 K using SRK with MR2 |
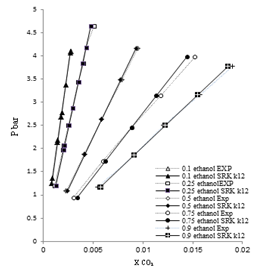 | Figure 3. Phase composition diagram of CO2- Mixture system at 298 K using SRK with MR1 |
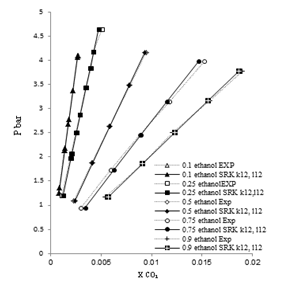 | Figure 4. Phase composition diagram of CO2- Mixture system at 298 K using SRK with MR2 |
 | Figure 5. Phase composition diagram of CO2- Mixture system at 308 K using SRK with MR1 |
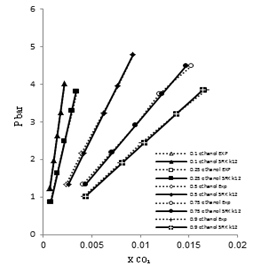 | Figure 6. Phase composition diagram of CO2- Mixture system at 308 K using SRK with MR2 |
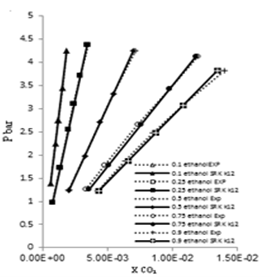 | Figure 7. Phase composition diagram of CO2- Mixture system at 323 K using SRK with MR1. |
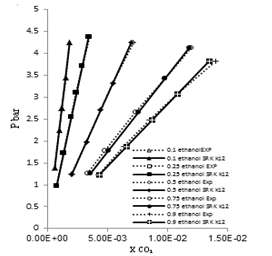 | Figure 8. Phase composition diagram of CO2- Mixture system at 323 K using SRK with MR2 |
These Figures indicated that the mixing rules MR2 gave %MAD smaller than the mixing rules MR1 for SRK -EOS. Thus, the MR2 with two adjustable parameter k12 and L12 can be used to calculate the gas-liquid equilibrium of CO2 (1)-mixture (2) at moderate pressures and different temperatures adequately. It is obvious that there is good agreement between calculated data from the model using (MR1, MR2) and experimental data. Although, there is small deviation especially in the mixture composition (0.25 ethanol + 0.75 water) and (0.9 ethanol + 0.1 Water) at the temperature 308, 323 K . However, this can be used to calculate the gas-liquid equilibrium properties of CO2 (1)-mixture (2) system.
4. Conclusoins
1. It is possible to collate gas-liquid equilibrium of CO2 – mixture system using SRK-EOS with the mixing rules of two adjustable parameters. 2. Mixing rule MR2 includes two adjustable parameter k12 and L12 can be employed to find the gas -liquid equilibrium data of CO2 (1)-mixture (2) at moderate pressures and different temperatures since it gives good agreement compared with the other mixing rules.3. It is acceptable to use MR1 that contain one adjustable parameter k12 to calculate gas -liquid equilibrium data of CO2 (1)-mixture (2) at moderate pressures and different temperatures since it gives good agreement.
References
| [1] | I. Dalmolin, E. Skovroinski, A. Biasi, and M. Corazza, “Solubility of carbon dioxide in binary and ternary mixtures with ethanol and water,” Fluid phase, 2006. |
| [2] | E. Wilhelm, R. Battino, and R. J. Wilcock, “Low-pressure solubility of gases in liquid water,” Chemical Reviews, vol. 77, no. 2, pp. 219–262, 1977. |
| [3] | O. Elizalde-Solis, L. A. Galicia-Luna, and L. E. Camacho-Camacho, “High-pressure vapor-liquid equilibria for CO2á+ áalkanol systems and densities of n-dodecane and n-tridecane,” Fluid Phase Equilibria, vol. 259, no. 1, pp. 23–32, 2007. |
| [4] | M. Hou, S. Liang, Z. Zhang, J. Song, T. Jiang, and B. Han, “Determination and modeling of solubility of CO2 in PEG200+ 1-pentanol and PEG200+ 1-octanol mixtures,” Fluid phase equilibria, vol. 258, no. 2, pp. 108–114, 2007. |
| [5] | O. Elizalde-Solis, “Solubility of thiophene in carbon dioxide and carbon dioxide + 1-propanol mixtures at temperatures from 313 to 363K,” Fluid phase equilibria, 2005. |
| [6] | J. Smith, H. Van Ness, and M. Abbott, “Introduction to chemical engineering thermodynamics, ISE,” 2001. |
| [7] | G. Soave, “Equilibrium constants from a modified Redlich-Kwong equation of state,” Chemical Engineering Science, vol. 27, no. 6, pp. 1197–1203, 1972. |
| [8] | S. M. Walas, Phase equilibria in chemical engineering, vol. 4. Butterworth Boston, 1985. |
| [9] | Y. Adachi and H. Sugie, “A new mixing rule–modified conventional mixing rule,” Fluid Phase Equilibria, vol. 28, no. 2, pp. 103–118, 1986. |
| [10] | V. N. Smith, H. C., Introduction to Chemical Engineering Thermodynamics, 4th ed. McGraw. Hill Book Company, 1987, p. 477. |

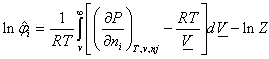
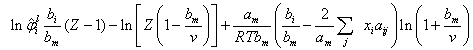
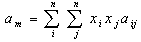
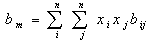
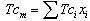
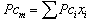
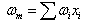
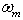 are the critical temperature, critical pressure and acentric factor for mixture. Tci, Pci,
are the critical temperature, critical pressure and acentric factor for mixture. Tci, Pci, 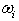 are the critical temperature and critical pressure and acentric factor for ethanol and water.xi , mole fraction of ethanol and water.Adjustable parameter (kij) is obtained from fitting experimental data using SRK-EOS. Additionally the adjustable parameter (Lij) which is used in MR2 is found by trial and error. The calculated parameter which is gives a good results, is shown in Table 4.
are the critical temperature and critical pressure and acentric factor for ethanol and water.xi , mole fraction of ethanol and water.Adjustable parameter (kij) is obtained from fitting experimental data using SRK-EOS. Additionally the adjustable parameter (Lij) which is used in MR2 is found by trial and error. The calculated parameter which is gives a good results, is shown in Table 4.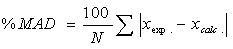








 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML



