-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Physical Chemistry
p-ISSN: 2167-7042 e-ISSN: 2167-7069
2011; 1(1): 1-9
doi: 10.5923/j.pc.20110101.01
Entropy Production from the Master Equation for Driven Lattice Gases
Sushma Kumar 1, Sara K. Ford 2, Kelsey C. Zielke 2, Paul D. Siders 2
1Department of Chemistry, Iowa State University, Ames, Iowa 55011, USA
2Department of Chemistry and Biochemistry, University of Minnesota Duluth, Duluth, Minnesota, 55812, USA
Correspondence to: Paul D. Siders , Department of Chemistry and Biochemistry, University of Minnesota Duluth, Duluth, Minnesota, 55812, USA.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Entropy production was calculated for the driven lattice gas on small two-dimensional square, hexagonal and triangular lattices. Steady-state and time-dependent properties were calculated with the master equation, using the complete transition matrix for all configurations. Entropy production from dissipated work or from probability current was the same for transition rates that preserved local detailed balance. Entropy production was calculated along several relaxation paths. Steady states, on all three lattices, were not states of either maximum or minimum entropy production.
Keywords: Driven Lattice Gas, Entropy, Entropy Production, Master Equation, Nonequilibrium Entropy
Cite this paper: Sushma Kumar , Sara K. Ford , Kelsey C. Zielke , Paul D. Siders , "Entropy Production from the Master Equation for Driven Lattice Gases", Physical Chemistry, Vol. 1 No. 1, 2011, pp. 1-9. doi: 10.5923/j.pc.20110101.01.
Article Outline
1. Introduction
- Driven non-equilibrium systems produce entropy. This work examines entropy production in a statistical-mechanical model that is simple enough so that calculations are transparent, include all system states, and require no approximations beyond numerical calculations. The system studied in this work is the driven lattice gas(DLG)[1-3] In the DLG model an external field drives particles across a lattice. There are pairwise attractions between particles. The freezing transition of the equilibrium lattice gas is modified by the field. Under some conditions, high-density strips with smooth interfaces are observed under the field’s action.Work done on the gas by the field is largely (at steady state, completely) exhausted to a heat bath. Dissipation of work to heat makes entropy production a property of the DLG, as it is of other driven systems. The hypothetical principle of maximum entropy production[4-10] or the converse principle of minimum entropy production would suggest that entropy production may be not just a property but an organizing principle of driven systems such as the DLG. Recent discussions of the role of entropy production in non-equilibrium systems include those by Ross, Vellela and Qian and Attard[11-13] A critical review of entropy-production ideas, giving a thorough historical perspective from Carnot’s work through the present, was written by Velasco, García-Colín and Uribe[14] The present work is a largely numerical study of the meaning and possible extrema of entropy production in the simple, well-defined DLG model. If DLG steady statesare characterized by extreme entropy production then entropy production will vary monotonically, either steadily rising or steadily falling on the way to steady state. Non-monotone total entropy production during relaxation, shown below, argues against entropy production as an adequate extremum principle for the DLG on small lattices.This work uses small lattices, small enough that the master equation is solved for the probabilities of all configurations. Issues of sampling and kinetic barriers, which are factors in interpreting Monte-Carlo and molecular dynamics results for large lattices, are avoided. A disadvantage of the small-lattice all-configuration method is that the results are not for the thermodynamic limit of infinite-size lattices. Dependence of entropy production on system size is likely to be complicated, as in a recent study of entropy production for a chemical reaction on a lattice, as a function of lattice size[15] The behavior of entropy production in the thermodynamic limit where extremum principles are intended to apply, is outside the scope of the present small-lattice work. The present work does not address applicability of an extremum entropy production principle for lattices of infinite size.The Kovacs effect, non-monotone relaxation following change in temperature,[16] is observed in the DLG. For the DLG, a more pronounced Kovacs-like effect is non- monotone relaxation following change in field strength.Nonequilibrium fluctuation theorems relate probabilities of positive and negative entropy production rates, as discussed in recent reviews[17,18] Fluctuation theorems are applicable to small systems, have been applied to stochastic systems,[19] and presumably could be applied to small driven lattice gases. However, because the present work focuses simply on entropy production, and not on its fluctuations, calculations of fluctuations in the driven lattice gas are outside the scope of this work.
2. Model
- This work used lattices small enough that the master equation could be solved for several eigenvectors. The largest lattices for which solutions were obtained had twenty four sites. In all cases lattices were half filled, because that gives the critical density in the case of zero field. The number of configurations of twelve particles on twenty four sites is 24!/(12!)2=2704156 configurations. Although calculations were done for lattices containing up to and including twenty four sites, and for all aspect ratios, this paper reports only results for these three 24-site lattices: 6×4 square, 4×3 triangular, and 2×3 hexagonal lattices. The lattice notation is nx×ny, where nx and ny are the number of unit cells in the x and y directions. The field, when nonzero, is in the y direction.
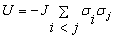 | (1) |
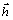 of one particle along one lattice edge. An external field of strength F biases particle hops. The work done by the field during one hop is
of one particle along one lattice edge. An external field of strength F biases particle hops. The work done by the field during one hop is 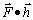 , which equals F cosθ because the lattice edge length is taken as the unit of length. The angle between a hop and the field or y axis is θ. Letting
, which equals F cosθ because the lattice edge length is taken as the unit of length. The angle between a hop and the field or y axis is θ. Letting 3. Methods
3.1. Representations
- All configurations of particles that fill half of the lattice sites were enumerated. Then symmetry operations were applied to group the configurations into symmetry-equivalent representations. The symmetry operations used were the identity plus translation in the field direction y by multiples of the unit cell. Symmetry reduced the 2704156 configurations to 676280 representations on the square lattice, 901432 representations both on the hexagonal and the triangular lattices. What are called representations in this work were called "relevant configurations" by Zhang[22,23] and Kumar[24] and "equivalence classes" by Zia, et al[25,26]
3.2. Transition Matrix
- The master equation for evolution of probabilities is
 | (2) |
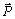 is the vector of probabilities. The rate matrix, W, is the square array of transition probabilities.Explicitly for the ith component of the vector of configuration probabilities,
is the vector of probabilities. The rate matrix, W, is the square array of transition probabilities.Explicitly for the ith component of the vector of configuration probabilities, 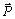 ,
, 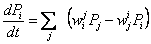 | (3) |
 | (4) |
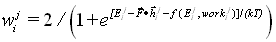 | (5) |
 is the one-particle hop that converts configuration j into configuration i, and
is the one-particle hop that converts configuration j into configuration i, and  is the work done by the field during the transition from j to i. The coupling function f is discussed in the entropy production section below, where it is used to explore violation of local detailed balance. For all other purposes in this work, f=0. In(5), k is Boltzmann’s constant, and T is the temperature of a bath that thermostats the lattice. The Glauber rate was chosen rather than the Metropolis rate or the van Beijeren-Schulman rate because the former is constant for all energetically favorable transitions and the latter rate tends to infinity for highly favorable transitions. To reduce memory requirements and save computing time, the master equation was solved for probabilities of representations rather than configurations. To operate on a vector
is the work done by the field during the transition from j to i. The coupling function f is discussed in the entropy production section below, where it is used to explore violation of local detailed balance. For all other purposes in this work, f=0. In(5), k is Boltzmann’s constant, and T is the temperature of a bath that thermostats the lattice. The Glauber rate was chosen rather than the Metropolis rate or the van Beijeren-Schulman rate because the former is constant for all energetically favorable transitions and the latter rate tends to infinity for highly favorable transitions. To reduce memory requirements and save computing time, the master equation was solved for probabilities of representations rather than configurations. To operate on a vector 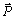 of representation probabilities, the transition matrix W is modified by multiplying each transition rate wji by a degeneracy factor.
of representation probabilities, the transition matrix W is modified by multiplying each transition rate wji by a degeneracy factor.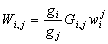 | (6) |
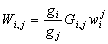 .Limitations of computer memory make storing large transition matrices difficult. Sparseness of the transition matrix W was essential to allow its storage and its use in calculating eigenvectors. The transition matrix for the 6×4 square lattice, for example, contains only 16194224 nonzero matrix elements. About 10−5 of its elements are nonzero. As Figure 2 shows, sparseness is similar for the square, triangular and hexagonal cases.
.Limitations of computer memory make storing large transition matrices difficult. Sparseness of the transition matrix W was essential to allow its storage and its use in calculating eigenvectors. The transition matrix for the 6×4 square lattice, for example, contains only 16194224 nonzero matrix elements. About 10−5 of its elements are nonzero. As Figure 2 shows, sparseness is similar for the square, triangular and hexagonal cases. 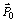 , which corresponds to steady state. Time dependence of probabilities is available from the full spectrum of eigenvalues and eigenvectors
, which corresponds to steady state. Time dependence of probabilities is available from the full spectrum of eigenvalues and eigenvectors 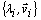 .
.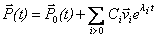 | (7) |
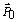 refers to the steady-state probability vector, (i.e., not the 0th component of an arbitrary vector) and for i>0,
refers to the steady-state probability vector, (i.e., not the 0th component of an arbitrary vector) and for i>0, 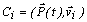 . The inner product is defined as[16,31]
. The inner product is defined as[16,31] | (8) |
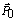 , that is, the probability of configuration j at steady state.
, that is, the probability of configuration j at steady state.3.3. Eigenvectors and Eigenvalues
- Explicit analytical expressions for the eigenvectors and eigenvalues of the master equation were obtained for six-site square lattices[22,24,26] For a six-site hexagonal lattice and an eight-site triangular lattice, Kumar used Mathematica to obtain analytical expressions for eigenvalues and eigenvectors[24] Such beautiful analytical results cannot easily be extrapolated to larger lattices.Large lattices are accessible by Monte Carlo simulation. Monte Carlo simulations have used tens of thousands[32] to a million sites[33] on square lattices. Even on the less-studied triangular and hexagonal lattices, Monte Carlo simulations have used thousands of sites[20] Simulation results for large systems are highly valuable. Of course, Monte Carlo simulations are entirely numerical and can be caught in kinetic traps, so that sampling the entire relevant configuration space can be difficult, especially at low temperature.The approach taken in this work is to use small enough matrices so that probabilities of all configurations are calculated. Because symbolic solutions are not sought, lattices are larger than those that were accessible to the earlier symbolic calculations, although still minute compared to those accessible to Monte Carlo simulations. Lattice sizes are limited primarily by memory available to store the transition matrix. Systems approaching the thermodynamic limit are outside the scope of this work. The value of the methods used in this work is that results are numerically exact and complete, explicitly including all configurations. For small enough matrices, through 12870 configurations, direct matrix methods of LAPACK and LAPACK++ were used. These calculations yielded the full spectrum of eigenvalues and eigenvectors.For larger matrices, the implicitly restarted Arnoldi method in the packages ARPACK[30] and ARPACK++[31] was used. ARPACK is well suited for calculating the several eigenvalues having largest real part (i.e., zero and negative but near zero) and their eigenvectors. The negative real parts of eigenvalues may be interpreted as rate coefficients or inverse time constants, as indicated in[7]. Excluding the null eigenvalue, each eigenvalue’s real part, after changing its sign, corresponds to inverse relaxation time along the corresponding eigenvector. It was suggested by van Kampen ([27] Ch. XIII Sec. 2) in the context of a different problem, that the largest(i.e., least negative) nonzero eigenvalue may correspond to symmetry breaking. In the present driven small-lattice gas, in every case calculated, the first eigenvector does have a nonzero first moment of density in the x direction, so it may be that relaxation occurs along that eigenvector. However, no broken-symmetry solutions were observed in the present systems. That is because the master equation(2) has but one null vector and the systems are too small to support a phase boundary. Nevertheless, properties (e.g., energy, internal entropy, current) of the present systems do suggest the large-system phase transitions.
3.4. Time Dependence
- Time dependence is in principle available from the full spectrum of eigenvalues and eigenvectors. However, because transition matrices are large the full spectrum was not calculated for the systems reported in this work. Rather, the master equation was integrated as a set of coupled differential equations, using Burkardt’s C++ version of RKF45[32]. The Runge-Kutta-Felhberg method with local extrapolation offers good stability and accuracy and low memory requirements[33] The method requires a relatively large number of matrix-vector multiplications. However, that operation was easily parallelized using openMP. The same matrix-vector multiplication method used for ARPACK eigenvector calculation also served for evaluating time derivatives.
3.5. Internal Entropy
- This work adopts the time-dependent extension of the Boltzmann-Gibbs entropy for the internal entropy of the system.
 | (9) |
3.6. Entropy Production
- The rate of internal entropy production is the time derivative of Ssys,(9), which can be written directly in terms of rate-matrix elements or in terms of probability currents, as below.
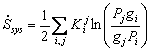 | (10) |
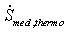 .
.  | (11) |
 | (12) |
 , following Zia and Schmittmann’s notation[27] The same quantity is denoted P by Schnakenberg[28] and simply dS/dt by Tomé and de Oliveira[29]Under some conditions on the transition rates and field, the thermodynamic and statistical entropy productions are equal. In the absence of an external drive, F=0, detailed balance ensures
, following Zia and Schmittmann’s notation[27] The same quantity is denoted P by Schnakenberg[28] and simply dS/dt by Tomé and de Oliveira[29]Under some conditions on the transition rates and field, the thermodynamic and statistical entropy productions are equal. In the absence of an external drive, F=0, detailed balance ensures 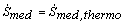 and
and , as it must be.With a nonzero external drive, F>0, detailed balance need not apply. However, a "local detailed balance"[19] may apply. Local detailed balance is equivalent to the f=0 case of
, as it must be.With a nonzero external drive, F>0, detailed balance need not apply. However, a "local detailed balance"[19] may apply. Local detailed balance is equivalent to the f=0 case of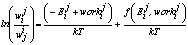 | (13) |
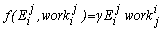 | (14) |
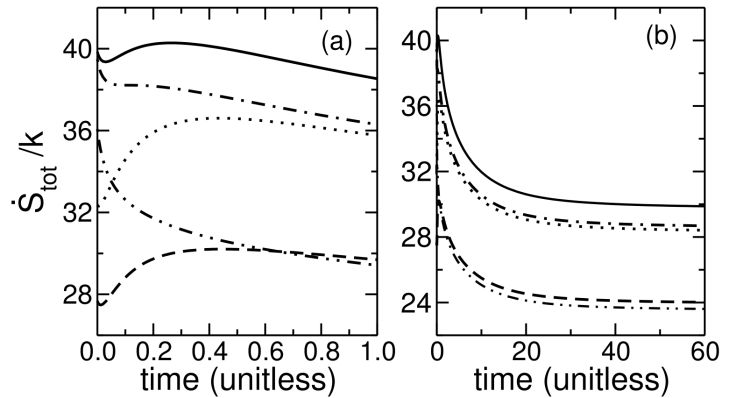
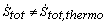 . Figure 3 shows the difference for the coupling function in(14) with γ=1/2 and γ=1. At γ=0 the statistical and thermodynamic entropy production rates are the same. When local detailed balance is violated, γ>0, the two dissipation rates differ greatly at short time. Subject to an additional assumption, Brey and Prados[40] showed
. Figure 3 shows the difference for the coupling function in(14) with γ=1/2 and γ=1. At γ=0 the statistical and thermodynamic entropy production rates are the same. When local detailed balance is violated, γ>0, the two dissipation rates differ greatly at short time. Subject to an additional assumption, Brey and Prados[40] showed  . As Figure 3 shows, the present system satisfies that inequality at short times (Figure 3a) but not at longer times(Figure 3b). The additional condition required by Brey and Prados for the inequality is that the steady state probability distribution be canonical, a condition that does not apply to the DLG.Solid line: γ=0, so
. As Figure 3 shows, the present system satisfies that inequality at short times (Figure 3a) but not at longer times(Figure 3b). The additional condition required by Brey and Prados for the inequality is that the steady state probability distribution be canonical, a condition that does not apply to the DLG.Solid line: γ=0, so  . Dash-dot line:
. Dash-dot line: 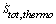 for γ=1/2. Dotted line:
for γ=1/2. Dotted line: 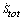 for γ=1/2. Dash-dot-dot line:
for γ=1/2. Dash-dot-dot line: 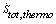 for γ=1. Dashed line:
for γ=1. Dashed line:  for γ=1.
for γ=1. 4. Entropy Production
4.1. Square Lattice
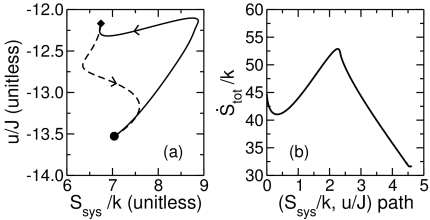
- Figure 4 shows the trajectory in (u/J, Ssys/k) from the equilibrium state to the F=4J steady state (solid line). Throughout the trajectory, the bath temperature was kT/J=0.55. The system was initially at equilibrium. Then an F=4J field was applied(t=0) and the master equation was integrated over time to the F=4J steady state. Along the integration path, energy and internal entropy were calculated. The return path in which the system was initially at the steady state under field F=4J is also shown(dashed line). For the return path, the field was reduced from 4J to zero at the initial time.
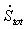 along the integration path is shown in Figure 5 for the first unit of time integration. The total entropy production rate is not monotone during relaxation to steady state, both falling and rising. The steady state has a lower entropy production rate than states from which it formed, so the F=4J steady state is not a state of maximum entropy production.
along the integration path is shown in Figure 5 for the first unit of time integration. The total entropy production rate is not monotone during relaxation to steady state, both falling and rising. The steady state has a lower entropy production rate than states from which it formed, so the F=4J steady state is not a state of maximum entropy production.4.2. Hexagonal and Triangular Lattices
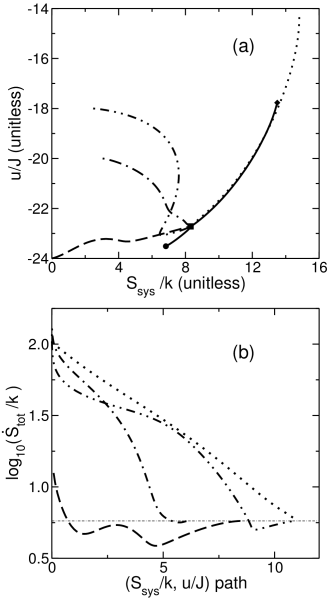
- Trajectories between steady states on a hexagonal lattice are shown in Figure 6, for which the bath temperature kT/J=0.33. Each trajectory has two points where the path turns. At those points the effective temperature Teff diverges. Approaching the F=0 steady state, kTeff/J≈kT/J=0.33, as expected. Approaching the F=4J steady state, kTeff/J≈2.4, which is consistent with the field heating the lattice gas.
5. Kovacs Effect
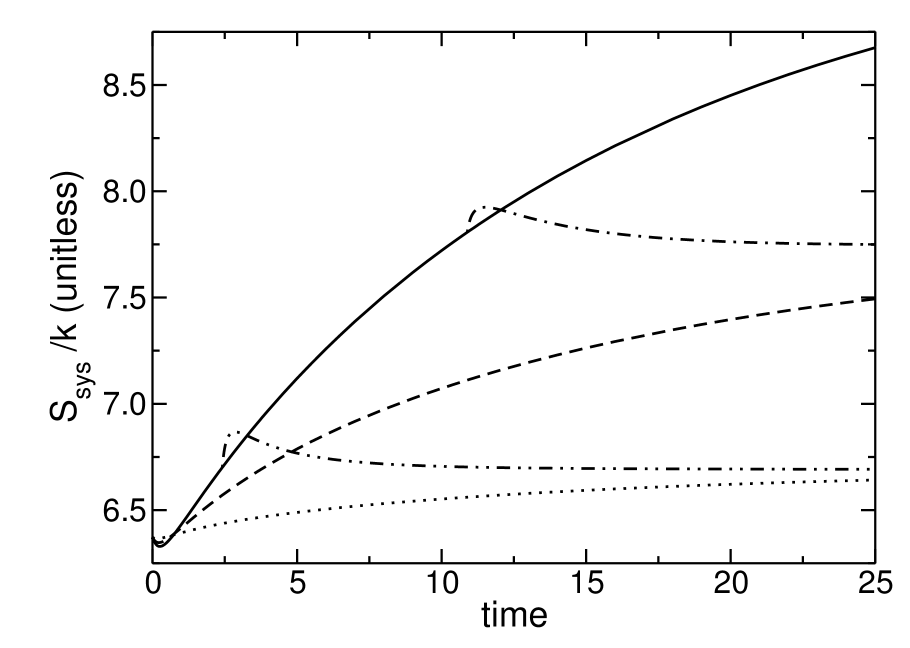
- Prados and Brey[16] describe the Kovacs effect as non-monotonic change of a system property during relaxation of the system from a non-equilibrium state to equilibrium. Commonly, temperature has been the control variable, with relaxation following an abrupt change in temperature. [16,43] The effect is observed as the system relaxes from one steady state to another. A property of the system(e.g., energy, internal entropy) is followed during relaxation. When the property reaches the value it would have been in an intermediate steady state, the control variable(e.g., temperature) is changed to that intermediate value. If the system were internally equilibrated to the intermediate steady state, its property would remain at the intermediate steady-state value and relaxation would be complete. The Kovacs effect is observed when the property continues changing before finally relaxing back to its intermediate steady-state value.Figure 8 shows typical Kovacs humps in Ssys/k during relaxation to driven steady states. The control variable is field strength rather than temperature. There is also a Kovacs effect when temperature is changed abruptly at fixed field strength, but because the effects found were small no figure showing temperature-induced Kovacs effects is included.The entropy-time paths of Figure 8 were prepared as follows. The steady state probabilities were calculated at kT/J=0.6 and F=4J. That was the initial state for all five lines. Under zero field, the state relaxed to the equilibrium state. Relaxation in the energy-entropy plane (not shown) followed a path similar to that shown as a dashed line in Figure 4, which is for a slightly lower temperature. Likewise, integration under fields of F=J and F=2J produced the entropy arcs rising toward steady states in Figure 8. To observe the Kovacs effect under F=2J, the F=4J-to-0 trajectory was followed toward equilibrium until Ssys/k=2.70, its F=2J steady-state value. At that time, t=2.42, the field strength was raised from zero to 2J, causing the system to begin relaxing to the F=2J steady state. Figure 8 shows that Ssys/k initially rose, producing the Kovacs hump, before falling back to its steady-state value. To observe the Kovacs effect at F=J, an analogous procedure was followed. The field was raised from zero to F=J at t=10.89 when Ssys/k=7.81, its F=J steady-state value.
6. Summary and Discussion
- The rate of entropy production in the surroundings of the lattice gas,
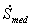 , was shown to be the same, whether calculated from probability current in the system or from heat transferred to the bath, as long as there was local detailed balance. In the absence of local detailed balance, the two measures of
, was shown to be the same, whether calculated from probability current in the system or from heat transferred to the bath, as long as there was local detailed balance. In the absence of local detailed balance, the two measures of  were unequal. The difference between statistical and thermodynamic
were unequal. The difference between statistical and thermodynamic 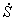 was illustrated in Figure 3 by calculations done with a non-local-detailed-balance rate function.Energy-entropy relaxation paths between steady states on square lattices indicated effective cooling by the external field. That cooling may be interpreted as causing the rise of critical temperature with increasing field strength. Entropy-energy paths for triangular lattices showed a smaller cooling effect. On the triangular lattice, the field increased both Ssys/k and u/J of steady states(Figure 7a), disordering the triangular-lattice gas. Energy-entropy paths on a hexagonal lattice were not simply explained. Hexagonal-lattice relaxation remains a subject for future research. The results showed that entropy production rate does not vary monotonically during relaxation of gases on the small square, hexagonal and triangular lattices. Maxima and minima of entropy production were observed along relaxation trajectories, so the steady state is not, generally, a state of either maximum or minimum entropy production. According to our observations, the principles of maximum or minimum entropy production at steady state do not apply to the lattice gas when driven upon the small lattices of this work. An alternative principle for selecting transitions, the principle of maximum second entropy,[13] will be explored in future work. The second or dynamical entropy is the number of configurations connected by a transition between macrostates in a specified time[44] For the driven lattice gas, a macrostate is a set of configurations that share a macroscopic property such as internal entropy. The subject for future study is to explore whether second entropy is maximized along relaxation paths to steady states of the driven lattice gas.
was illustrated in Figure 3 by calculations done with a non-local-detailed-balance rate function.Energy-entropy relaxation paths between steady states on square lattices indicated effective cooling by the external field. That cooling may be interpreted as causing the rise of critical temperature with increasing field strength. Entropy-energy paths for triangular lattices showed a smaller cooling effect. On the triangular lattice, the field increased both Ssys/k and u/J of steady states(Figure 7a), disordering the triangular-lattice gas. Energy-entropy paths on a hexagonal lattice were not simply explained. Hexagonal-lattice relaxation remains a subject for future research. The results showed that entropy production rate does not vary monotonically during relaxation of gases on the small square, hexagonal and triangular lattices. Maxima and minima of entropy production were observed along relaxation trajectories, so the steady state is not, generally, a state of either maximum or minimum entropy production. According to our observations, the principles of maximum or minimum entropy production at steady state do not apply to the lattice gas when driven upon the small lattices of this work. An alternative principle for selecting transitions, the principle of maximum second entropy,[13] will be explored in future work. The second or dynamical entropy is the number of configurations connected by a transition between macrostates in a specified time[44] For the driven lattice gas, a macrostate is a set of configurations that share a macroscopic property such as internal entropy. The subject for future study is to explore whether second entropy is maximized along relaxation paths to steady states of the driven lattice gas.ACKNOWLEDGEMENTS
- This research was supported in part by the National Science Foundation through TeraGrid resources provided by the National Center for Supercomputing Applications(cobalt). This work also relied upon computer access granted by the Minnesota Supercomputing Institute of the University of Minnesota. Additional computing resources were provided by the Department of Chemistry and Biochemistry and the Visualization And Digital Imaging Laboratory of the University of Minnesota Duluth. Authors Ford and Zielke gratefully acknowledge support from the University of Minnesota’s Undergraduate Research Opportunities Program and the Department’s Summer Undergraduate Research Program.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML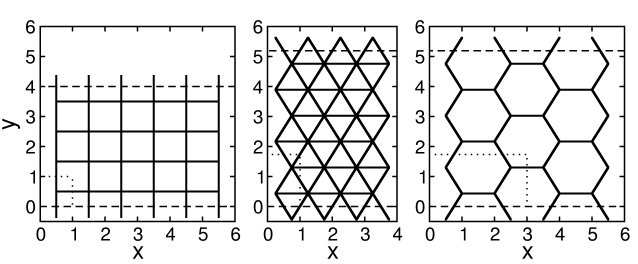


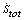 , solid line, and effective temperature, dashed line, for the initial part of the equilibrium-to-F=4J trajectory shown in Figure 4. The dotted line is the bath temperature, kT/J=0.55
, solid line, and effective temperature, dashed line, for the initial part of the equilibrium-to-F=4J trajectory shown in Figure 4. The dotted line is the bath temperature, kT/J=0.55