1. Introduction

The analysis of complex luminescence decays explained the dynamics of recombination center yields. The relaxation of different physical systems has been found to follow the stretched-exponential law. In particular, the photoluminescence from glassy materials and other solids [1-3] have been reported in the literature to behave this way.

In this paper we present the fluorescence decay profiles of ⁴S_3/2à⁴I_15/2 transition in Er³⁺- doped zinc tellurite glass (TZG) at various doping concentrations between 0.2 and 3% (molar). We show that the fluorescence decay profile can be fitted with the stretched exponential function. We have explained that lattice defect sites may interact through a dipolar energy transfer mechanism [4-7].

2. Experimental Details

Glasses were prepared from oxide powders of TeO₂, ZnO and Er₂O₃ as starting materials using the conventional melt-quenching method. The material used in our measurement has a composition of 70TeO₂–30ZnO. The amount of dopant was varied between 0.2 and 3 mol% Er₂O₃. The intrinsic lifetimes of the levels were obtained by exciting the samples with a laser analytical systems dye laser pumped by a pulsed frequency doubled Nd: YAG laser from BM Industries. The duration of pulses was 8 ns. The emitted light has been focused on a Jobin–Yvon HR S2 spectrophotometer. The detection has been performed using an R 1767 Hammamatsu photomultiplier and a Lecroy 9410 averager oscilloscope. All experiments were performed at room temperature.

3. Results and Discussion

The luminescence decay of homogeneously doped TeO₂-ZnO: Er³⁺ was non-exponential due to non radiative energy transfer processes. Analysis of the photoluminescence decay profiles of Er³⁺ showed that the energy transfer between Er³⁺ ions was active only for concentrations beyond 0.5 mol%.

We have investigated the luminescence decay of the ⁴S_3/2à⁴I_15/2 transition in order to analyze the dynamics of this energy transfer. Figure 1 depicts the photoluminescence decay profiles of Er³⁺, measured for different ion concentrations. The luminescence decay was strongly non-exponential with ion concentration dependent time constant. We have found that the rapid decay of the relaxation curve increases with ion concentrations. It is shown that the experimental results of the photoluminescence decay can be described by the stretched exponential function:

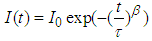(1)

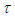Where is an effective time constant and β is a constant between 0 to 1.

For values β < 1 the decay is slower than the comparable exponential decay with the same 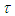factor.

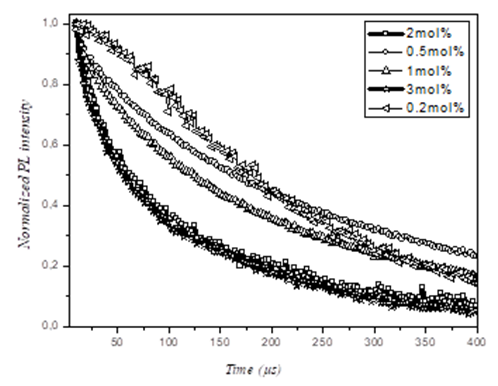Figure 1. Stretched exponential fit to the decay from the 4S3/2 level of the TZG, under 550 nm pumping

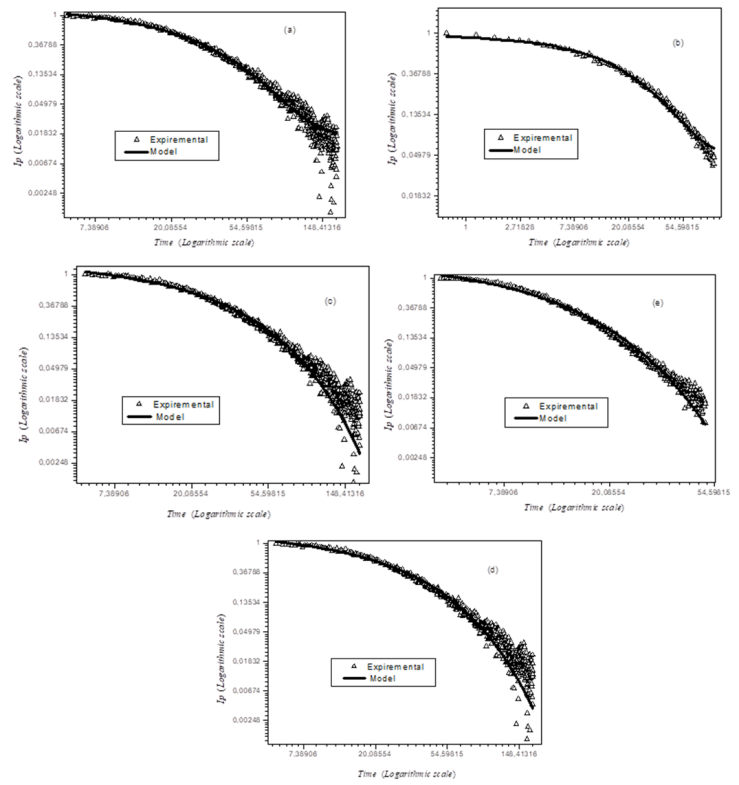Figure 2. The normalized intensity of the photoluminescence versus the normalized time, for 0.2 (a), 0.5(b), 1(c), 2(d) and 3(e) mol% Er3+ concentration

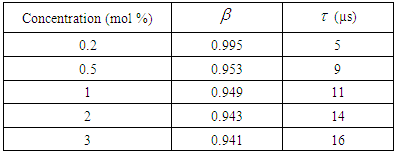
The values of measured parameters β and , obtained from the fit of photoluminescence decay data with use of equation 1 (in Figure 2). The parameters obtained from stretched exponential fits to the photoluminescence decay from the ⁴S_3/2 level of the zinc tellurite glass samples are listed in Table 1, for different Er³⁺ ion concentrations ranging from 0.2 to 3 mol %. The function shows decreasing values of β with increasing concentration of Er³⁺. The stretched exponential spans the largest dynamic range of β (from 0.995 to 0.941). For the 0.2 mol % ion concentration, the stretched exponential function was very similar to the single exponential results with value of very close to one (0.995). This implies that there is one radiative recombination pathway for excited ions. This proposal is supported by the fact that energy transfer between excited ions can be ignored in the case of a low ion concentration [8]. In the following, we assume that the dominant radiative and multiphonon decay times component reflect the total decay time, and obtain from the relation: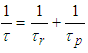

(2)

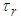where is the radiative lifetime of the emitting level ⁴S_3/2 and 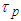is the multiphonon lifetime. To evaluate the first decay time, the intensity parameters have been calculated using the Judd-Ofelt formulae [9,10]. The obtained value for this lifetime is 203 µs with use of Ω₂ = 1.15, Ω₄ = 4.59 and Ω₆ = 2.7010^-20 cm² respectively. The lifetime 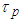has been computed using the model of multiphonon relaxation proposed by Riseberg and Moos [11] and for which this decay time is given by the relationship:

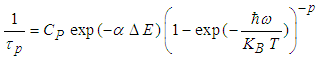(3)

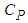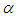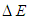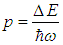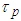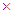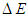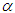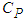where and are non-radiative parameters which depend on the host material, represents the energy gap between two successive levels and is the number of phonons emitted in the relaxation process. In the case of the ⁴S_3/2-⁴I_15/2 transition, the value of , calculated from Eq. (3) at T=300 K, is of magnitude 1.5510³ s. The parameters used for this calculation are: = 7400 cm^-1, = 4.710^-3 cm, = 6.3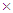10¹¹ and 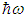≈ 750 cm^-1 respectively [12]. We will, now, study the effects of the Er³⁺ ion concentration on the total decay time 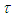. When this concentration increases, the energy transfer takes place. Thus the decay time characterizing this process must be considered in the calculation of 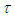. We labeled this decay time 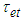. Then, Eq. (3) will be rewritten as:

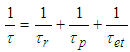(4)

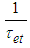Using the latter equation, we can deduce the energy transfer rate from the photoluminescence intensity measurements.

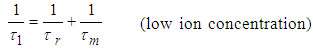(5)

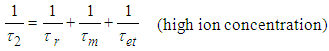(6)

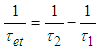(7)

Where τ_r, τ_m, τ_et are the radiative, multiphonon and energy transfer lifetimes of the ⁴S_3/2 level, respectively.

Figure 3 displays the decay rate as a function of the square of the Er³⁺ ion concentration.

The linear behavior indicates that energy transfer process due to dipole-dipole interaction in Er³⁺- Er³⁺ pairs. The theory for this process was initially developed by Dexter for multi-polar coupling [13], the energy transfer rate occurring by an electric dipole interaction is proportional to the inverse of the sixth power of the distance separating the two ions and consequently to the squared concentration. This model supposes that the Er³⁺ ion pairs are homogeneously distributed in the host lattice.

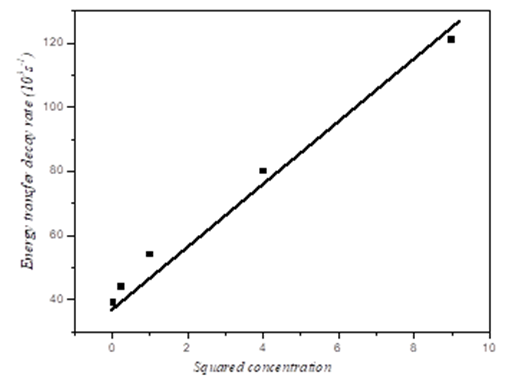Figure 3. The decay rate as a function of the square of the Er3+ ion concentration

If the observed non-exponential decay is a result of inter-ion energy transfer then, according to the expressions presented in Eq. 1, the photoluminescence decay should become increasingly non-exponential with donor concentration. On the other hand, if the non-exponential decay is a result of the finite distribution of multi-phonon decay rates caused by the inhomogeneous nature of the host glasses then the degree of non-exponentiality should be independent of donor concentration. But, the stretched exponential power obtained from the fits show a dependence on the Er³⁺ concentration, for concentrations as high as 0.5 mol%. This result found that the energy transfer process involving the ⁴S_3/2 level has not a negligible effect on the decay dynamics of the ⁴S_3/2 at these concentration levels. It can also be concluded from the presence of concentration dependence in this sample set, that inter-ion energy transfer mechanisms are the cause of the non-exponential behaviour from this manifold. Also, this leads to the second most probable cause for the reduction in the stretched exponential power, the host composition. The host composition has been shown a normal increase in fluorescence lifetime of the ⁴S_3/2 level, which indicates that it has insignificant impact on the local environment surrounding the Er³⁺ ion. It is therefore proposed that the incorporation of Er³⁺ has not modified the local environment which could involve decreasing the amount of inhomogeneous broadening and therefore the low distribution of possible multi-phonon decay rates in the system.

Table 1. Lifetimes and stretched exponential of the 4S3/2 level as a function of Er3+ concentration

4. Conclusions

A model of nonexponential behaviour is considered from the point of view of contribution of dipole-dipole interactions. We may conclude that the dipolar interaction dominates the energy transfer in this system and the incorporation of rare earth ions is made difficult by the structure of the network.

With this in mind, the reduction in stretched exponential power observed with the increase in the Er³⁺ concentration, may indicate that the energy transfer processes affect the decay dynamics of this level for Er³⁺ concentrations.