| [1] | F. F. Sene, J. R. Martinelli, and L. Gomes, "Optical and structural characterization of rare earth doped niobium phosphate glasses," J. Non-Cryst. Solids 348 (2004) 63-71. |
| [2] | W. Mekhum, N. Sangwaranatee, A. Thapinta, P. Attaphut, P. Limsuwan, H. Kim, M. Djamal and J. Kaewkhao, "Visible Luminescence Properties of Sm3+ Doped Magnesium Bismuth Phosphate Glasses," Eng. Mater. 675-676 (2016) 405-408. |
| [3] | S. Kumar, P. Vinatier, A. Levasseur and K. J. Rao, "Investigations of structure and transport in lithium and silver borophosphate glasses," J. Solid State Chem. 177 (2004) 1723-1737. |
| [4] | A.G. Dias, J. M. S. Skakle, I. R. Gibson, M. A. Lopes and J. D. Santos, "In situ thermal and structural characterization of bioactive calcium phosphate glass ceramics containing TiO2 and MgO oxides: High temperature – XRD studies," J. Non-Cryst. Solids 351 (2005) 810-817. |
| [5] | R. K. Brow, " Review: the structure of simple phosphate glasses," J. Non-Cryst. Solids 263–264 (2000) 1-28. |
| [6] | T. Minami and J. D. Mackenzie, "Thermal expansion and chemical durability of phosphate lasses," J. Am. Ceram. Soc. 60 (1977) 232-235. |
| [7] | L. Baia, R. Stefan, J. Popp, S. Simon and W. Kiefer, "Vibrational spectroscopy of highly iron doped B2O3–Bi2O3 glass systems," J. Non-Cryst. Solids 324 (2003)109-117. |
| [8] | S. Bale, M. Purinima, Ch. Srinivasu and S. Rahman, "Vibrational spectra and structure of bismuth based quaternary glasses," J. Alloys Compd. 457 (2008) 545-548. |
| [9] | I. Ardelean and D. Rusu, "Structural investigations of some Bi2O3 based glasses," J. Opt. Adv. Mater. 10 (2008) 66-73. |
| [10] | C. Stehle, C. Vira, D. Vira, D. Hogan, S. Feller and M. Affatigato, "Optical and physical properties of bismuth borate glasses related to structure," Phys. Chem. Glasses 39 (1998) 83-86. |
| [11] | T. Komatsu, R. Sato, K. Imai, K. Matusita and T. Yamashita, Jpn. J. Appl. Phys. 27(1998) L550. |
| [12] | Y. Fujimoto and M. Nakatsuka, "Infrared Luminescence from Bismuth-Doped Silica Glass," Jpn. J. Appl. Phys. 40 (2001) L279. |
| [13] | X. Meng, J. Qiu, M. Peng, D. Chen, Q. Zhao, X. Jiang, and C. Zhu, "Near infrared broadband emission of bismuth-doped aluminophosphate glass," Opt. Exp. 13 (2005) 1628-1634. |
| [14] | F. El-Diasty, M. Abdel-Baki, F. A. Abdel-Wahab, "Oxyfluoro aluminum-borate host glass: interband gap study and estimation of radiative lifetime for luminescent dopant ions," Opt. Quant. Electron. 48 (2016) 273-284. |
| [15] | F. Berkemeier, S. Voss, A.W. Imre, H. Mehrer, "Molar volume, glass-transition temperature, and ionic conductivity of Na- and Rb-borate glasses in comparison with mixed Na–Rb borate glasses," J. Non-Cryst. Solids 351 (2005) 3816-3825. |
| [16] | B. Bridge, A. A. Higazy, “Model of the compositional dependence of the elastic moduli of polycomponent oxide glasses,” Phys. Chem. Glasses 27 (1986) 1-14. |
| [17] | M. Born and E. Wolf, “Principle of Optics,” Pergamon Press (1984). |
| [18] | M. Abdel-Baki and F. El-Diasty, “Role of oxygen on the optical properties of borate glass doped with ZnO,” J. Solid State Chem. 43 (2011) 2762-2769. |
| [19] | V. Dimitrov and T. Komatsu “Effect of interionic interaction on the electronic polarizability, optical basicity and binding energy of simple oxides,” J. Ceram. Soc. Jpn. 107 (1999) 1012-1018. |
| [20] | R. R. Tummala and E. J. Rymaszewski, “Microelectronics Packaging Handbook,” Van Nostrand Reinhold. New York (1989). Chap. I. |
| [21] | V. N. Rai, B. N. R. Sekhar, P. Tiwari, R. J. Kshirsagar and S. K. Deb, "Spectroscopic studies of gamma irradiated Nd doped phosphate glasses," J. Non-Cryst. Solids 357 (2011) 3757–3764. |
| [22] | I-H. Lee, S-H. Shin, F. Foroutan, Nilay J. Lakhkar, M-S. Gong and J. C. Knowles, "Effects of magnesium content on the physical, chemical and degradation properties in a MgO−CaO−Na2O−P2O5 glass system," J. Non-Cryst. Solids 363 (2013) 57–63. |
| [23] | E. Mansour and G. El-Damrawi, "Electrical properties and FTIR spectra of ZnO–PbO–P2O5 glasses," Physica B 405 (2010) 2137–2143. |
| [24] | H.S. Liu, T.S. Chin and S.W. Yung, "FTIR and XPS studies of low-melting PbO-ZnO-P2O2 glasses," Mater. Chem. Phys. 50 (1997) 1–10. |
| [25] | P. Pascuta, G. Borodi, A. Popa, V. Dan and E. Culea, "Influence of iron ions on the structural and magnetic properties of some zinc-phosphate glasses," Mater. Chem. Phys. 123 (2010) 767–771. |
| [26] | J. Jiraˇık, L. Koudelka, J. Pospisil, P. Moˇsner, L. Montagne and L. Delevoye, "Study of structure and properties of ZnO–Bi2O3–P2O5 glasses," J. Mater. Sci. 42 (2007) 8592-8598. |
| [27] | L. Baia, T. Iliescu, S. Simon and W. Kiefer, "Raman and IR spectroscopic studies of manganese doped GeO2–Bi2O3 glasses," J. Mol. Struct. 599 (2001) 9-13. |
| [28] | A. A. Kharlamov, R. M. Almeida and J. Heo, "Vibrational spectra and structure of heavy metal oxide glasses," J. Non-Cryst. Solids 202 (1996) 233-240. |
| [29] | P.Y. Shih, S. W. Yung and T. S. Chin, "FTIR and XPS studies of P2O5–Na2O–CuO glasses," J. Non-Cryst. Solids 244 (1999) 211-222. |
| [30] | A. Chahine, M. Et-Tabirou and J. L. Pascal, "Structural investigations of (50-x)Na2O.xBi2O3.10CuO. 40P2O5 glasses using FTIR and Raman spectroscopies," Phys. Chem. Glasses 45 (2004) 32-36. |
| [31] | S. HyeokIm, Y. H. Na , N. J. Kim, D, H. Kim, C. W. Hwang and B. K. Ryu, "Structure and properties of zinc bismuth phosphate glass," Thin Solid Films 518 (2010) e46–e49. |
| [32] | D. E. C. Corbridge and E. J. Lowe, "The infra-red spectra of some inorganic phosphorus compounds," J. Chem. Soc. (1954) 493-502 (Resumed). |
| [33] | P. SrinivasaRao, Ch. Rajyasree, A. R. Babu, P. M. Vinaya Teja and D. K. Rao, "Effect of Bi2O3 proportion on physical, structural and electrical properties of zinc bismuth phosphate glasses," J. Non-Cryst. Solids 357 (2011) 3585–3591. |
| [34] | P. Subbalakshmi and N. Veeraiah, "Dielectric dispersion and certain other physical properties of PbO–Ga2O3–P2O5 glass system," Mater. Lett. 56 (2002) 880-888. |
| [35] | A. Shain, M. Et-tabirou, L. Montagne and G. Palavit, "Role of bismuth and titanium in Na2O–Bi2O3–TiO2–P2O5 glasses and a model of structural units," Mater. Res. Bull. 37 (2002) 2459-2466. |
| [36] | A. Chahine and M. Et-tabirou, "Structural study of (50 − x)Na2O–xCuO–10Bi2O3–40P2O5 glasses," Mater. Res. Bull. 37 (2002) 1973-1979. |
| [37] | M. F. Zhang, S. J. Shi, J. X. Meng, X. Q. Wang, H. Fan, Y. C. Zhu, X. Y. Wang, Y. T. Qian, “Preparation and characterization of near-infrared luminescent bifunctional core/shell nanocomposites,” J. Phys. Chem. C 112 (2008) 2825. |
| [38] | Y. H. Wang, Y. Y. Zuo, H. Gao, “Luminescence properties of nanocrystalline YVO4:Eu3+ under UV and VUV excitation,” Mater. Res. Bull. 41 (2006) 2147-. |
| [39] | R. Meltzer, S. Feofilov, B. Tissue, H. B. Yuan “Dependence of fluorescence lifetimes of Y2O3:Eu3+ nanoparticles on the surrounding medium,” Phys. Rev. B 60 (1999) 14012-. |
| [40] | E. V. Golyeva, D. V. Tolstikova, I. E. Kolesnikov, M. D. Mikhailov, “Effect of synthesis conditions and surrounding medium on luminescence properties of YVO4:Eu3+ nanopowders,” J. Rare Earths 33 (2015) 129-134. |
| [41] | R. J. Wiglus, T. Grzyb, S. Lis and W. Strek. “Hydrothermal preparation and photoluminescent properties of MgAl2O4:Eu3+ spinel nanocrystals,” J. Lumin. 130 (2010) 434-441. |
| [42] | B. Henderson and G. F. Imbusch, “Optical Spectroscopy of Inorganic Solids,” Clarendon Press, Oxford, 1989, p. 173. |
| [43] | M. J. Weber, “Science and technology of laser glass,” J. Non-Cryst. Solids 123 (1990) 208-222. |
| [44] | R. Reisfeld, “Spectra and energy transfer of rare earths in inorganic glasses,” Struct. Bonding 13 (1973) 53. |
| [45] | R. Reisfeld, “Radiative and nonradiative transition of rare earths in glasses,” Struct. Bonding 22 (1975) 123. |
| [46] | J. A. Duffy, M. D. Ingram, in: D. Uhlman, N. Kreidl (Eds.), Optical Properties of Glass, American Ceramic Society, Westerville, 1991. |
| [47] | J. A. Duffy, “Electronic polarisability and related properties of the oxide ion,” Phys. Chem. Glasses 30 (1989) 1-4. |



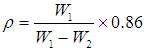
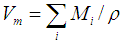
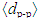 was calculated. The phosphate molar volume
was calculated. The phosphate molar volume 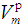 was calculated by [15]:
was calculated by [15]: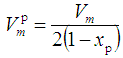
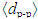 was calculated using the expression [16]:
was calculated using the expression [16]: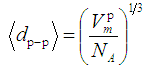
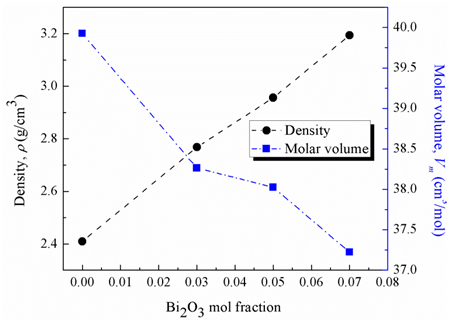
 1023 g/mol). Fig. 2 illustrates that the increase in Bi2O3 content decreases the average phosphate-phosphate separation. The merging of Bi2O3 on the expense of P2O5 leads to a significant densification of the glass.
1023 g/mol). Fig. 2 illustrates that the increase in Bi2O3 content decreases the average phosphate-phosphate separation. The merging of Bi2O3 on the expense of P2O5 leads to a significant densification of the glass. 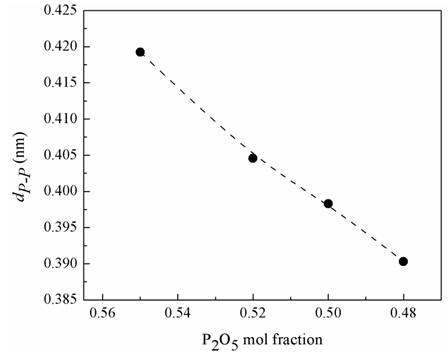
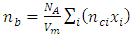
 1021 cm-3 (sample 1) to 89
1021 cm-3 (sample 1) to 89  1021 cm-3 (sample 4). Accordingly, the insertion of Bi2O3 may lead to a decrease in the phosphate-phosphate intermolecular separation and an increase in the number of bonds per unit volume.
1021 cm-3 (sample 4). Accordingly, the insertion of Bi2O3 may lead to a decrease in the phosphate-phosphate intermolecular separation and an increase in the number of bonds per unit volume.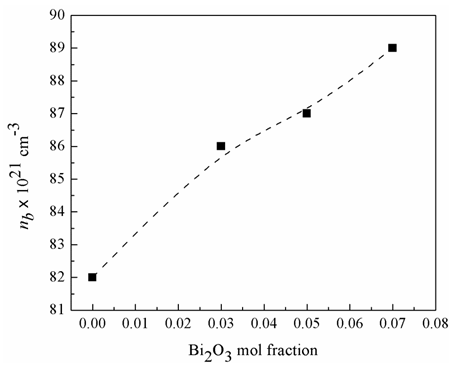
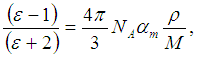
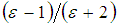 is defined as the molar reflectivity term. The glass molar electronic polarizability, αm, is expressed as the summation of the electronic polarizabilities of constituent ions, αi, and that of oxygen ion,
is defined as the molar reflectivity term. The glass molar electronic polarizability, αm, is expressed as the summation of the electronic polarizabilities of constituent ions, αi, and that of oxygen ion, 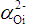 , by [18]:
, by [18]: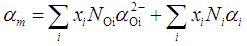
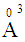 , 0.094
, 0.094 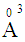 and 1.508
and 1.508 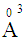 for P3+, Mg2+ and Bi3+ ions, respectively [19]. In the same sequence, the electronic polarizabilities of an oxygen ion,
for P3+, Mg2+ and Bi3+ ions, respectively [19]. In the same sequence, the electronic polarizabilities of an oxygen ion,  , were 1.350
, were 1.350 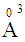 , 1.687
, 1.687 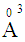 and 3.507
and 3.507 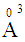 , respectively [19]. It can be seen that (Fig 4) increase in Bi2O3 mol. fraction increases the glass molar polarizability which increases the optical dielectric constant of the investigated glass. An increase in the optical dielectric constant in the order of 15.5% was obtained with the increase in the Bi2O3 mol fraction up to 7%. The calculated optical dielectric constant makes the glass appropriate for advanced photonic applications like microelectronic and luminescent devices [20].
, respectively [19]. It can be seen that (Fig 4) increase in Bi2O3 mol. fraction increases the glass molar polarizability which increases the optical dielectric constant of the investigated glass. An increase in the optical dielectric constant in the order of 15.5% was obtained with the increase in the Bi2O3 mol fraction up to 7%. The calculated optical dielectric constant makes the glass appropriate for advanced photonic applications like microelectronic and luminescent devices [20].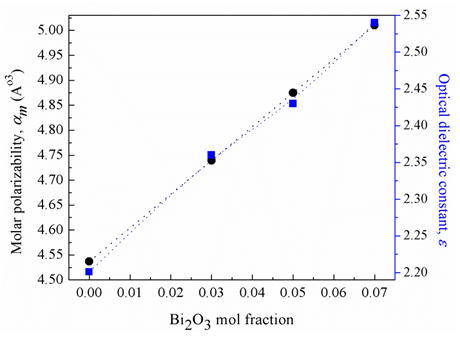
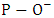 in Q2 units at 1084 cm-1 [23, 24].3. Asymmetric stretching vibrations of P–O–P bonds at 929 cm-1 [24, 25].4. Symmetric stretching vibration of P–O–P chains at 776 cm-1 [25].
in Q2 units at 1084 cm-1 [23, 24].3. Asymmetric stretching vibrations of P–O–P bonds at 929 cm-1 [24, 25].4. Symmetric stretching vibration of P–O–P chains at 776 cm-1 [25].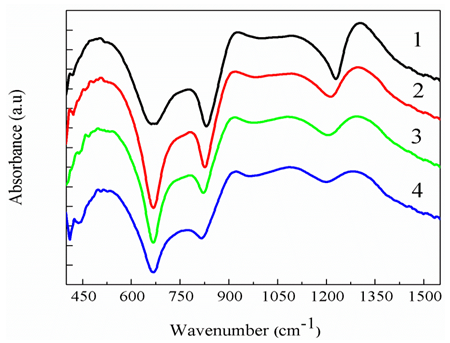
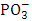 groups [33-36] which is due to the cleavage of P=O bonds and formation of more ionic P―O―Bi and P―O− bond group terminators that consist of non-bridging oxygens. A rapid depolymerization of the phosphate chains with increasing Bi2O3 contents is shown with the formation of P–O–Bi bonds and BiO6 octahedral in the glass matrix. The stretching vibration of PO3 groups was a sign of increasing covalent character of the P–O–Bi bonds. This covalent character supports the glass forming ability for the Bi6+ ions.
groups [33-36] which is due to the cleavage of P=O bonds and formation of more ionic P―O―Bi and P―O− bond group terminators that consist of non-bridging oxygens. A rapid depolymerization of the phosphate chains with increasing Bi2O3 contents is shown with the formation of P–O–Bi bonds and BiO6 octahedral in the glass matrix. The stretching vibration of PO3 groups was a sign of increasing covalent character of the P–O–Bi bonds. This covalent character supports the glass forming ability for the Bi6+ ions.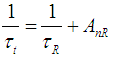
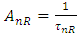 is the probability of non-radiative processes and τnR is the non-radiative lifetime. The radiative lifetime should be much shorter than the non-radiative lifetime to possess a competent luminescence. The expression giving the radiative lifetime for the electronic transitions of the embedded ion in the host glass was given by [42]:
is the probability of non-radiative processes and τnR is the non-radiative lifetime. The radiative lifetime should be much shorter than the non-radiative lifetime to possess a competent luminescence. The expression giving the radiative lifetime for the electronic transitions of the embedded ion in the host glass was given by [42]: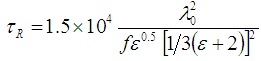
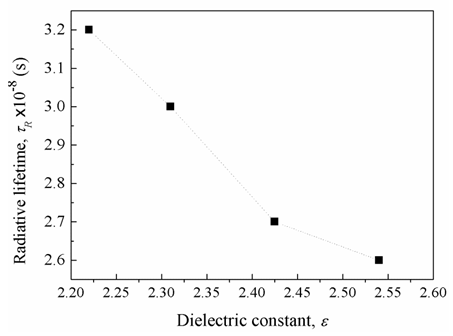
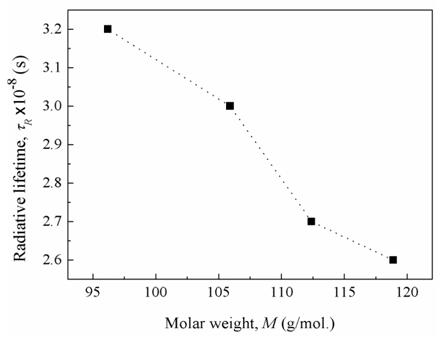
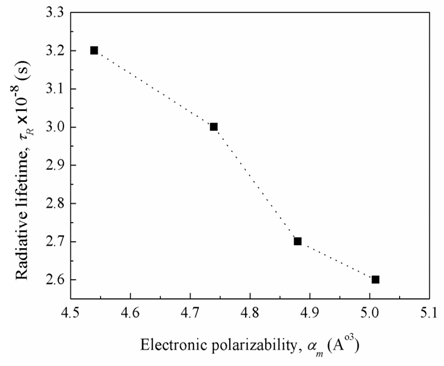
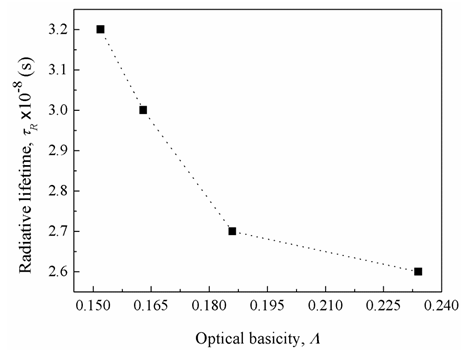
 , (by 7.4%) and the glass electronic polarizability, αm, (by 10.3 %) which were associated with increasing the Bi2O3 content, the radiative lifetime was decreased by 19%. The observed trend confirms that the spectroscopic properties of doped ions will be strongly affected by the structure of host glass [43-45] and by the conversion of Bi3+ into Bi6+ ions (which have more polarizing power and smaller field strength).
, (by 7.4%) and the glass electronic polarizability, αm, (by 10.3 %) which were associated with increasing the Bi2O3 content, the radiative lifetime was decreased by 19%. The observed trend confirms that the spectroscopic properties of doped ions will be strongly affected by the structure of host glass [43-45] and by the conversion of Bi3+ into Bi6+ ions (which have more polarizing power and smaller field strength).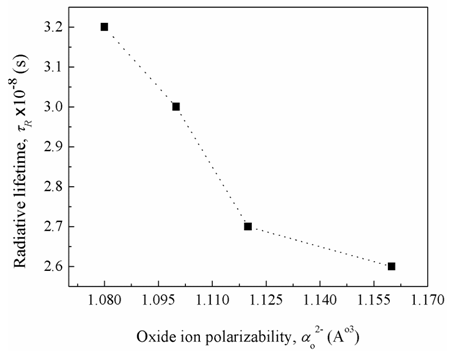
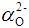 , was given by [47]:
, was given by [47]: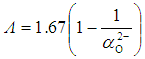
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML