-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Optics and Applications
p-ISSN: 2168-5053 e-ISSN: 2168-5061
2016; 6(3): 47-51
doi:10.5923/j.optics.20160603.01

Temperature Dependence of Internal Quantum Efficiency in SiGe Lasers
Hassan Kaatuzian , Alireza Jorkesh
Photonics Research Laboratory (PRL), E.E. Department, Amirkabir University of Technology, Tehran, Iran
Correspondence to: Alireza Jorkesh , Photonics Research Laboratory (PRL), E.E. Department, Amirkabir University of Technology, Tehran, Iran.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Recently, SiGe lasers have been widely developed in research centers. Their applications in high-speed facilities and recent improvements have made them interesting R&D subjects. One characteristic which needs to be studied is internal quantum efficiency having an important role in laser quality. In studies presented until now, the temperature has been presumed to be constant; An assumption that will fade as the lasers perform in the experiments. After a little operation, the temperature increases and even with large fans, it somehow impossible to fix this factor. We present a study of this characteristic for SiGe lasers in various temperatures by studying recombination rate and its dependence on temperature. Meanwhile, we will present a way which enhances this factor to higher percentages. Changing the temperature, we can obtain different efficiencies which can lead to various applications.
Keywords: Internal Quantum Efficiency, Temperature dependence in lasers, Temperature in IQE
Cite this paper: Hassan Kaatuzian , Alireza Jorkesh , Temperature Dependence of Internal Quantum Efficiency in SiGe Lasers, International Journal of Optics and Applications, Vol. 6 No. 3, 2016, pp. 47-51. doi: 10.5923/j.optics.20160603.01.
Article Outline
1. Introduction
- Semiconductor lasers play important roles for Silicon-based photonic technology and among semiconductors, Ge is suggested as the only material capable of conforming to the CMOS standards and also be a light emitter for photonic integration [1]; however, progresses in optical communications demand for low-cost high-speed technology and thus, SiGe-based devices are promising solutions for filling these gaps [2].Two types of quantum efficiency for different lasers are often considered:External Quantum Efficiency (EQE) is the ratio of the number of charge carriers collected by the emitting cell to the number of photons of a given energy shining on outside (incident photons).Internal Quantum Efficiency (IQE) is the ratio of the number of charge carriers collected by the emitting cell to the number of photons of a given energy, shining on the cell from outside and are absorbed by the cell itself.The IQE is always larger than the EQE. A low IQE indicates that the active layer of the laser is unable to make good use of the photons. To measure the IQE, first, we need to measure the EQE of the laser devices. Then, its transmission and reflection need to be measured and combined to infer the IQE. The ideal quantum efficiency graph has a square shape, where the QE value is fairly constant across the entire spectrum of wavelengths measured; However, the QE for most solar cells is reduced because of the effects of recombination, where charge carriers are not able to move into an external circuit. The same mechanisms that affect the collection probability also affect the QE. For example, modifying the front surface can influence carriers generation near the surface [3, 4].Internal quantum efficiency can be obtained by dividing the number of electrons per second to the number of absorbed photons per second. Although deriving an exact formula which can get us to complete understanding of this discussion has been calculated formerly, it is challenging to understand which parts are dependent on temperature [5].It is very interesting to know a way which could change this property. In this article, we will do our best to modify the dependence of this property on temperature and enhance it.
2. Theoretical Background for IQE Estimation
- The recombination rate of carriers in a single-quantum-well device is given by the so-called ABC model.
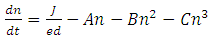 | (1) |
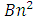 is the rate of radiative recombination and
is the rate of radiative recombination and 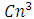 is the Auger recombination rate. At steady state, the relation between the current and carrier density is given by (2).
is the Auger recombination rate. At steady state, the relation between the current and carrier density is given by (2).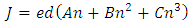 | (2) |
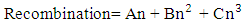 | (3) |
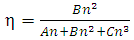 | (4) |
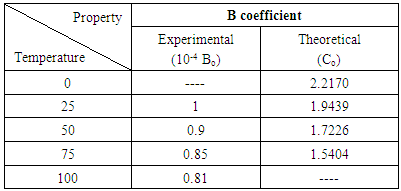
2.1. Bimolecular Recombination Coefficient
- Basically, this coefficient is defined by as followed:
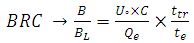 | (5) |
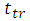 is the capacitance transit time and
is the capacitance transit time and 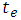 is extraction time. Both of these components do not depend on temperature because these two are always fixed constants and are dependent on the material itself. The only factor needed to study is
is extraction time. Both of these components do not depend on temperature because these two are always fixed constants and are dependent on the material itself. The only factor needed to study is 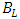 because all other factors are fixed for a special kind of material [7].C is the capacitance which only depends on the shape of the laser. The only reason that can change this factor is the temperature where it can lead to the expansion of layers. As the changes are at last 300 degrees centigrade, we can easily ignore this item and presume it fixed. It will be really helping in other parts.
because all other factors are fixed for a special kind of material [7].C is the capacitance which only depends on the shape of the laser. The only reason that can change this factor is the temperature where it can lead to the expansion of layers. As the changes are at last 300 degrees centigrade, we can easily ignore this item and presume it fixed. It will be really helping in other parts.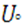 is the applied voltage known as
is the applied voltage known as 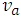 , too. Since the source for applying this voltage is invariable, this factor is not dependent on temperature [8].First,
, too. Since the source for applying this voltage is invariable, this factor is not dependent on temperature [8].First, 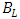 can be obtained by (6).
can be obtained by (6).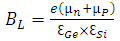 | (6) |
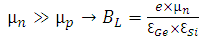 | (7) |
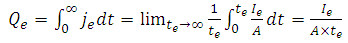 | (8) |
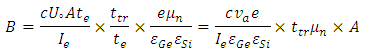 | (9) |
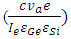 are completely invariant and do not change as temperature changes. The only changing factors are
are completely invariant and do not change as temperature changes. The only changing factors are 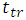 and
and 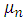 . So, the final equation can be simplified as (10).
. So, the final equation can be simplified as (10).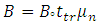 | (10) |
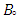 is the invariant proportion. Mobility dependence on temperature has been modified in data books.
is the invariant proportion. Mobility dependence on temperature has been modified in data books.2.2. Auger Coefficient
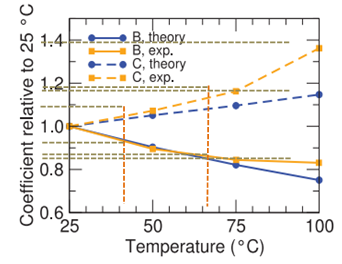
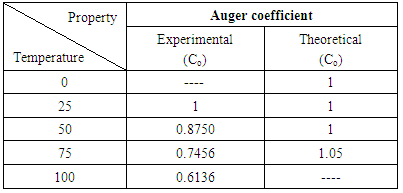
- Auger coefficient can be differently modified based on various circumstances and materials. Figure 1. shows the three main auger coefficients. As it can be observed in this figure, Auger coefficient can be radiative, direct, and indirect [9].
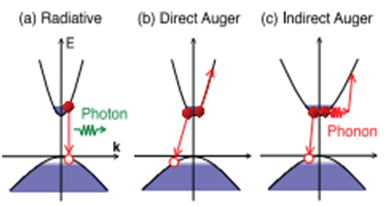 | Figure 1. Radiative, Direct, and Indirect Auger coefficient |
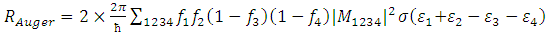 | (11) |
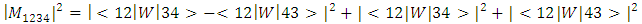 | (12) |
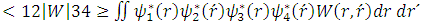 | (13) |
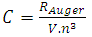 | (14) |
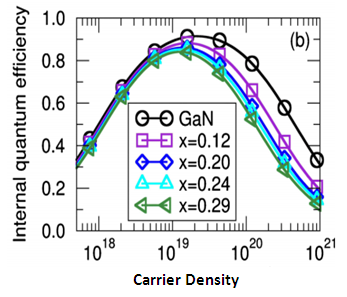 | Figure 2. Internal Quantum Efficiency based on different number of dopants |
3. Simulation and Discussion
- As it was mentioned earlier, IQE can be obtained by (4). Since the carrier density in SiGe lasers are mostly high and they are highly doped, equation (4) can be simplified as (15).
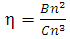 | (15) |
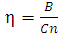 | (16) |
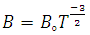 | (17) |
|
|
|
|
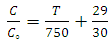 | (18) |
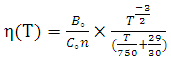 | (19) |
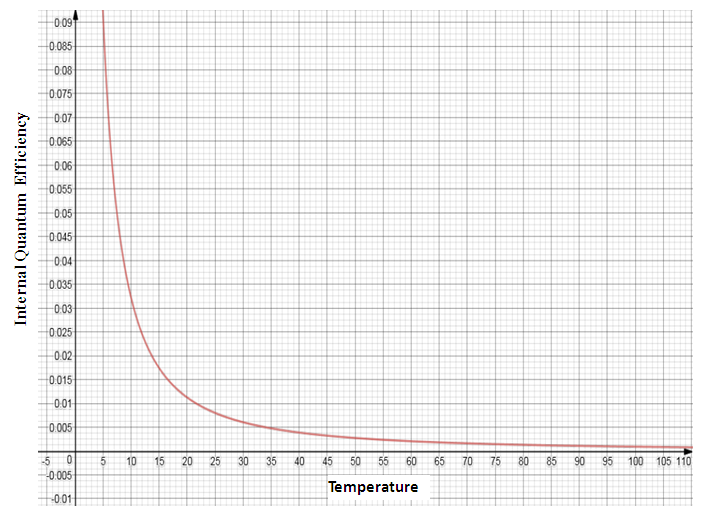 | Figure 4. IQE in different temperatures using MATLAB for drawing based on equation (17) |
4. Conclusions
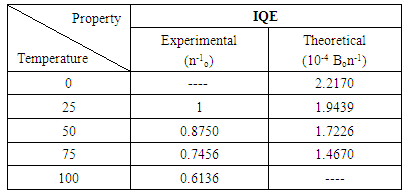
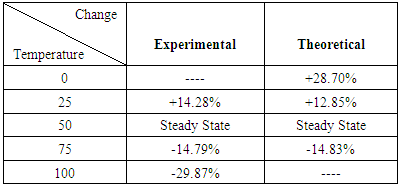
- As it has been declared in table 4, the temperature has a main effect on IQE. Changing this factor can lead to a wide range of variation of this characteristic. By getting the temperature near icing temperature, IQE can be enhanced by 28.7%. This is an essential result since by improving this characteristic, we can have well-functioned lasers with higher efficiencies.It is also important to know that temperature controlling is an essential process which can change this function. In the case which there is no application of fans, the temperature can get as high as 100°C which will decrease the IQE percentage as much as 29.87%.In this article, we tried to work on the IQE and define different parts of it for conducting a function based on temperature. We could also get to an improvement of 28.70% in this characteristic. IQE was calculated at different temperatures which are mostly ignored and assumed fixed.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML