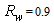-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Optics and Applications
p-ISSN: 2168-5053 e-ISSN: 2168-5061
2015; 5(3): 82-102
doi:10.5923/j.optics.20150503.05
Optics of Solar Concentrators. Part III: Models of Light Collection of 3D-CPCs under Direct and Lambertian Irradiation
Antonio Parretta1, 2, Erica Cavallari2
1ENEA C.R. “E. Clementel”, Via Martiri di Monte Sole 4, Bologna (BO), Italy
2Physics Department, University of Ferrara, Via Saragat 1, Ferrara (FE), Italy
Correspondence to: Antonio Parretta, ENEA C.R. “E. Clementel”, Via Martiri di Monte Sole 4, Bologna (BO), Italy.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
The optical properties of nonimaging solar concentrators irradiated in direct mode by diffused Lambertian beams are investigated in detail adopting original simulation methods. These methods were not limited to investigate useful properties for the practical application of the concentrators, but were also used to study them as optical elements with specific transmission, reflection and absorption characteristics. We have investigated, therefore, besides the flux transmitted to the receiver, also the flux back reflected from input aperture and that absorbed on the wall of the concentrator. We have simulated the transmission, reflection and absorption efficiencies, the average number of reflections of the transmitted or reflected rays, their angular divergence and the distribution of flux on the receiver and on the internal wall surface, as function of the angular divergence of the input beam and of the reflectivity of the internal wall. The presented simulation methods can be fruitfully applied to any other type of solar concentrator.
Keywords: Solar concentrator, Light collection, Optical simulation, Optical modeling, Nonimaging optics
Cite this paper: Antonio Parretta, Erica Cavallari, Optics of Solar Concentrators. Part III: Models of Light Collection of 3D-CPCs under Direct and Lambertian Irradiation, International Journal of Optics and Applications, Vol. 5 No. 3, 2015, pp. 82-102. doi: 10.5923/j.optics.20150503.05.
Article Outline
1. Introduction
- A review of the theoretical models of light irradiation and collection in solar concentrators (SC) was presented in the first part of this work [1]. In the second part [2] we presented the optical simulations of those models applied to nonimaging SC irradiated by direct and collimated beams. The importance of this irradiation lies in the fact that it represents the typical operating condition of a SC. We have chosen, for the optical simulations, a class of nonimaging SC of the type 3D-CPC (Three-Dimensional Compound Parabolic Concentrators) [3-9] to be used mainly as primary elements of a concentrator system. In this paper we extend the study of these SC by investigating diffused irradiation conditions, which are well represented by lambertian beams (beams with constant radiance) with variable angular aperture. The results of our work can be extended in this way to CPC used as secondary elements of concentration. Our interest on these SC is that they allow to reach very high concentration levels, comparable to the theoretical ones, and that their optical transmission efficiency is quite constant within a defined angle of incidence of the input beam. A further advantage of these SC is that they operate with reflective surfaces that do not induce spectral dispersion of light. We have simulated the optical behavior of the nonimaging SC by investigating its transmission, reflection and absorption properties, and we have defined new optical quantities. In particular, we have examined: i) the transmitted flux in terms of the optical transmission efficiency, average number of internal reflections of the transmitted rays, spatial distribution of the flux density on the receiver, angular distribution of radiance at the exit aperture; ii) the flux reflected from the input aperture in terms of reflection efficiency, angular divergence and average number of reflections; iii) the absorbed flux in terms of absorption efficiency and distribution of the absorbed flux on the internal wall of the CPC. In this way, all the optical features of the SC, considered as a generic optical element interacting with a lambertian beam, were analyzed. The methods of simulation and elaboration of the optical data presented in this work can be considered as general tools for the analysis of any other optical device.
2. The Compound Parabolic Concentrator (CPC)
- The Compound Parabolic Concentrator (CPC) is a nonimaging concentrator developed by R. Winston [3] to efficiently collect Cherenkov radiation in high energy experiments. Since then, the nonimaging concentrators have been widely used to concentrate sunlight [4-18]. The CPC is a reflective concentrator with a profile obtained by the combination of two parabolas, and is characterized by a step-like transmission efficiency allowing the efficient collection of light from 0° to a maximum angle, the acceptance angle
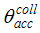 , where the suffix “coll” means that the irradiation is done with a collimated beam.Fig. 1 shows the 3D-CPC used in this work for the optical simulations. It is the same that was used in the previous paper of this series [2]. It is characterized by a maximum divergence of rays at exit aperture equal to 90°, and then only two independent parameters are required for defining its shape.
, where the suffix “coll” means that the irradiation is done with a collimated beam.Fig. 1 shows the 3D-CPC used in this work for the optical simulations. It is the same that was used in the previous paper of this series [2]. It is characterized by a maximum divergence of rays at exit aperture equal to 90°, and then only two independent parameters are required for defining its shape.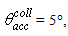 and the length L = 150 mm. The focal length of the parabolic profile, f = 1.14 mm, the radius of input aperture, a = 12.035 mm, and the radius of output aperture, a’ = 1.052 mm, become [2]:
and the length L = 150 mm. The focal length of the parabolic profile, f = 1.14 mm, the radius of input aperture, a = 12.035 mm, and the radius of output aperture, a’ = 1.052 mm, become [2]: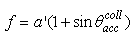 | (1) |
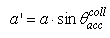 | (2) |
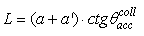 | (3) |
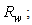 all the other added devices (absorbers, screens, etc.) were external to the concentrator and were used only as tools to improve the knowledge of its optical properties. For the reflectivity of the internal wall we have used only high values (0.8÷1.0); when not specified, it is equal to 1 (no optical loss inside the concentrator). All the optical simulations were carried out by using the TracePro ray-tracing software of Lambda Research [19].The flux at input of the CPC is a Lambertian flux characterized by a constant radiance
all the other added devices (absorbers, screens, etc.) were external to the concentrator and were used only as tools to improve the knowledge of its optical properties. For the reflectivity of the internal wall we have used only high values (0.8÷1.0); when not specified, it is equal to 1 (no optical loss inside the concentrator). All the optical simulations were carried out by using the TracePro ray-tracing software of Lambda Research [19].The flux at input of the CPC is a Lambertian flux characterized by a constant radiance  and by a variable angular aperture
and by a variable angular aperture 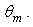 The total flux at input is then a function of
The total flux at input is then a function of 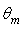 and is expressed by [1]:
and is expressed by [1]: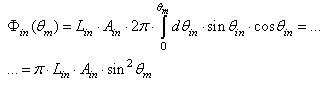 | (4) |
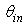 is the incident polar angle. In order to keep constant the radiance at input of the CPC, we have used in the simulations a number of input rays, that is an input flux, proportional to
is the incident polar angle. In order to keep constant the radiance at input of the CPC, we have used in the simulations a number of input rays, that is an input flux, proportional to 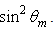
3. Analysis of the Transmitted Flux
3.1. Analysis of the Total Flux Transmitted to Receiver
- To study the flux transmitted to the exit aperture of the CPC, we have closed the exit aperture by an ideal absorber, so all the rays reaching the aperture can be counted and analyzed by the simulation program [19]. The flux transmitted to the exit aperture is given by:
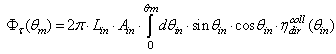 | (5) |
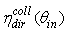 is the transmission efficiency of the CPC under direct and collimated irradiation, and is a function of the incident polar angle
is the transmission efficiency of the CPC under direct and collimated irradiation, and is a function of the incident polar angle  [1, 2] (see Fig.2).
[1, 2] (see Fig.2).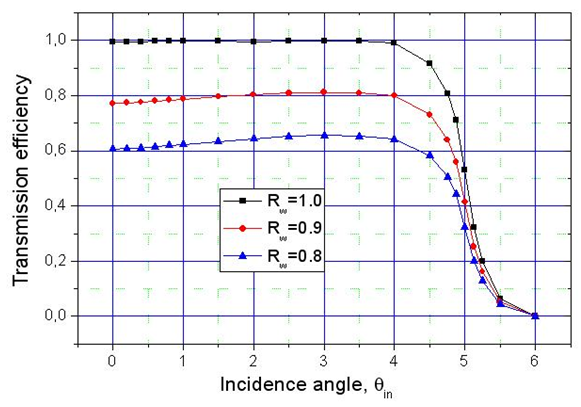 | Figure 2. Optical transmission efficiency 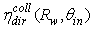 of the 3D-CPC calculated for three wall reflectivities: of the 3D-CPC calculated for three wall reflectivities: 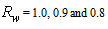 |
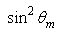 rule (see Eq. (4)), corresponding, in this simulation, to 50k rays at
rule (see Eq. (4)), corresponding, in this simulation, to 50k rays at 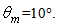 Fig. 3 shows the number of the incident, transmitted and reflected rays vs.
Fig. 3 shows the number of the incident, transmitted and reflected rays vs. 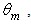 measured for a unitary wall reflectivity. In this case we have no optical loss on the wall of the CPC, but only loss due to the back reflected rays. We can see that, as long as
measured for a unitary wall reflectivity. In this case we have no optical loss on the wall of the CPC, but only loss due to the back reflected rays. We can see that, as long as 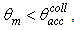 due to the square shape of the transmission efficiency of the CPC (see Fig. 2), all the input rays are transmitted, whereas, at
due to the square shape of the transmission efficiency of the CPC (see Fig. 2), all the input rays are transmitted, whereas, at 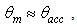 the transmitted rays stop growing and the reflected rays begin to appear and grow following the growth of the incident rays.
the transmitted rays stop growing and the reflected rays begin to appear and grow following the growth of the incident rays.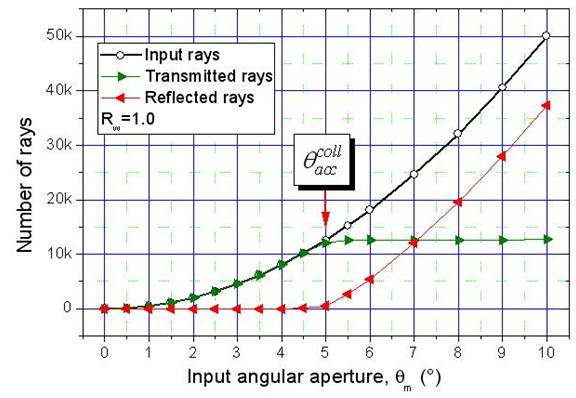 | Figure 3. Number of incident, transmitted and reflected rays vs. the angular aperture of the Lambertian beam 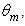 calculated for a unitary wall reflectivity calculated for a unitary wall reflectivity |
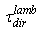 [1].This quantity refers to an angular aperture of the Lambertian beam equal to 90°. If the lambertian beam at input is limited by the angular aperture
[1].This quantity refers to an angular aperture of the Lambertian beam equal to 90°. If the lambertian beam at input is limited by the angular aperture  the above quantity becomes
the above quantity becomes 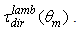 We have added the term "dir" to distinguish the Lambertian beam that we send to the entrance aperture of the concentrator, from the Lambertian beam that we send to the exit aperture of the concentrator, and that we will indicate by the term "inv". The properties of a CPC concentrator irradiated by an “inverse” Lambertian beam will be discussed in a future paper of this series. The Lambertian transmission efficiency of the CPC is expressed [1] by the ratio between output and input flux:
We have added the term "dir" to distinguish the Lambertian beam that we send to the entrance aperture of the concentrator, from the Lambertian beam that we send to the exit aperture of the concentrator, and that we will indicate by the term "inv". The properties of a CPC concentrator irradiated by an “inverse” Lambertian beam will be discussed in a future paper of this series. The Lambertian transmission efficiency of the CPC is expressed [1] by the ratio between output and input flux: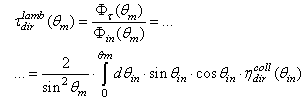 | (6) |
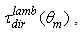 simulated for a unitary wall reflectivity, is shown in Fig. 4. It is interesting to compare the behavior of
simulated for a unitary wall reflectivity, is shown in Fig. 4. It is interesting to compare the behavior of 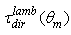 with that of
with that of 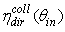 (see Fig.2). We obtain a step-like transmission efficiency curve also for a Lambertian beam irradiation, with the efficiency almost constant until about the acceptance angle
(see Fig.2). We obtain a step-like transmission efficiency curve also for a Lambertian beam irradiation, with the efficiency almost constant until about the acceptance angle 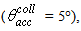 but, differently from the transmission efficiency curve
but, differently from the transmission efficiency curve 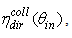 now the
now the 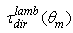 curve decreases slowly at increasing
curve decreases slowly at increasing 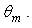 The reason is that, for
The reason is that, for 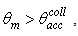 a constant portion of the input beam is always collected, and the Lambertian transmission efficiency at these conditions can be expressed by (on the assumption that
a constant portion of the input beam is always collected, and the Lambertian transmission efficiency at these conditions can be expressed by (on the assumption that 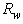 =1.0):
=1.0):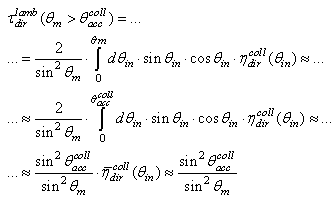 | (7) |
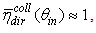 as it can be seen from the curve of Fig. 2 corresponding to
as it can be seen from the curve of Fig. 2 corresponding to 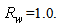 Fig. 4 shows the Lambertian transmission efficiency of the CPC compared to the
Fig. 4 shows the Lambertian transmission efficiency of the CPC compared to the 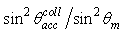 function. The perfect correspondence between the two curves when
function. The perfect correspondence between the two curves when 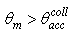 is clearly evident.
is clearly evident.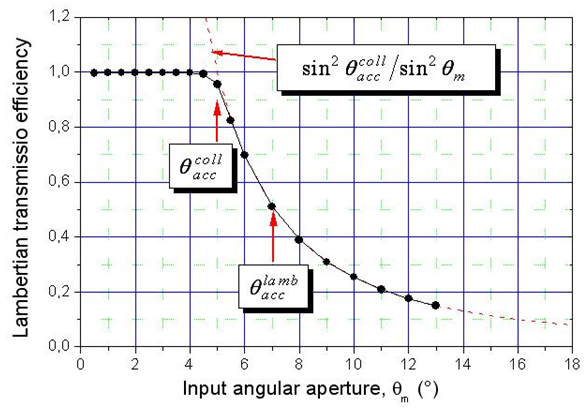 | Figure 4. Lambertian transmission efficiency of the CPC calculated as function of the angular aperture of the Lambertian beam, 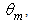 for a unitary wall reflectivity for a unitary wall reflectivity |
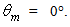 We call this angle the “Lambertian acceptance angle”,
We call this angle the “Lambertian acceptance angle”, 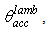 indicated in Fig. 4 together with
indicated in Fig. 4 together with 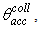 the acceptance angle at parallel beam irradiation. The quantity
the acceptance angle at parallel beam irradiation. The quantity 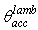 is immediately derived from Eq. (7), and is about 7.1° for our CPC with
is immediately derived from Eq. (7), and is about 7.1° for our CPC with 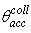 = 5.0°:
= 5.0°: 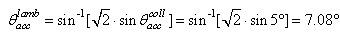 | (8) |
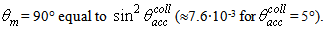 Until now we have not yet analyzed the effect of
Until now we have not yet analyzed the effect of  on the studied quantities. We do it starting with the direct Lambertian transmittance, calculated for three wall reflectivities:
on the studied quantities. We do it starting with the direct Lambertian transmittance, calculated for three wall reflectivities: 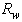 =1.0, 0.9 and 0.8 (see Fig. 5).
=1.0, 0.9 and 0.8 (see Fig. 5). 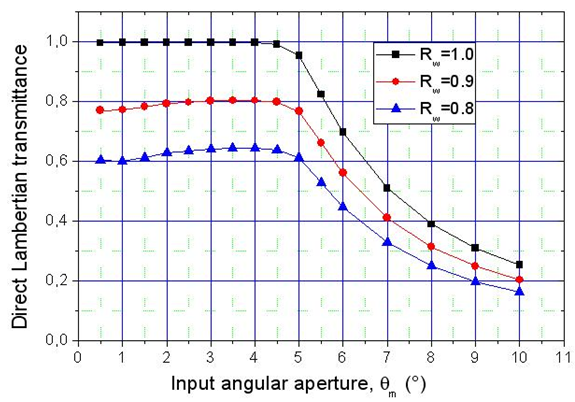 | Figure 5. The Lambertian transmission efficiency calculated for three different wall reflectivities: 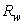 =1.0; 0.9 and 0.8 =1.0; 0.9 and 0.8 |
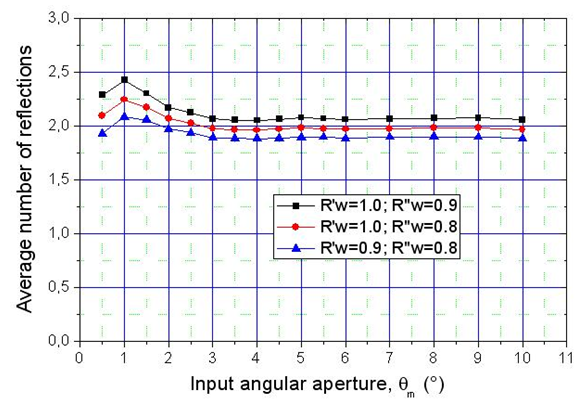
3.2. Average Number of Reflections of the Total Absorbed Rays
- The analysis of the three curves of
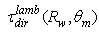 allows deriving the average number of reflections experienced by the transmitted rays. In this regard we will make use of a formula similar to Eq. (24) used in [2], replacing
allows deriving the average number of reflections experienced by the transmitted rays. In this regard we will make use of a formula similar to Eq. (24) used in [2], replacing 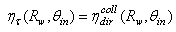 with
with 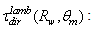
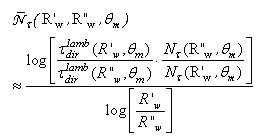 | (9) |
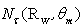 represents the number of transmitted rays. The average number of reflections has been calculated by using three pairs of wall reflectivities: (1.0-0.9); (1.0-0.8); (0.9-0.8). The results are reported in Fig. 6 and show that the average number of reflections of the transmitted rays is practically independent on the angular aperture of the Lambertian beam and equal to ≈2. This result is in good agreement with what was found [2] by analyzing the average number of reflections of the transmitted beam when the CPC is irradiated with a parallel beam at different polar angles respect to the optical axis.
represents the number of transmitted rays. The average number of reflections has been calculated by using three pairs of wall reflectivities: (1.0-0.9); (1.0-0.8); (0.9-0.8). The results are reported in Fig. 6 and show that the average number of reflections of the transmitted rays is practically independent on the angular aperture of the Lambertian beam and equal to ≈2. This result is in good agreement with what was found [2] by analyzing the average number of reflections of the transmitted beam when the CPC is irradiated with a parallel beam at different polar angles respect to the optical axis.3.3. Lambertian Concentration Ratio
- We now introduce the quantity “direct Lambertian concentration ratio”,
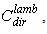 defined in [1] as the ratio between the average output, or transmitted, radiance and the constant input radiance. When the lambertian beam at input has an angular aperture
defined in [1] as the ratio between the average output, or transmitted, radiance and the constant input radiance. When the lambertian beam at input has an angular aperture 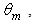 the direct Lambertian concentration ratio is indicated as
the direct Lambertian concentration ratio is indicated as 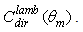 We start calculating the average output radiance:
We start calculating the average output radiance: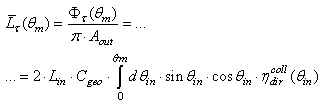 | (10) |
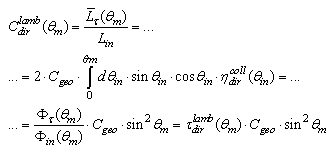 | (11) |
 expressed in (W/mm2·sr) and calculated for three wall reflectivities:
expressed in (W/mm2·sr) and calculated for three wall reflectivities:  =1.0, 0.9 and 0.8.
=1.0, 0.9 and 0.8. 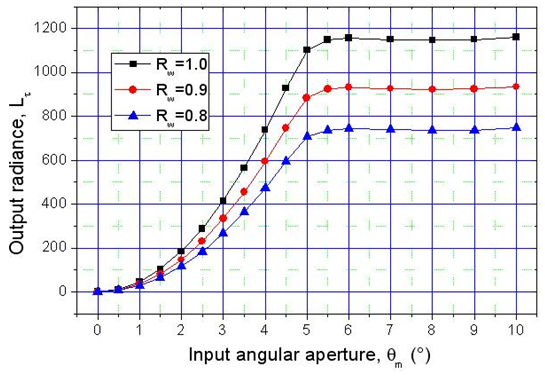 | Figure 7. Average output radiance 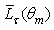 of the transmitted flux, calculated for three wall reflectivities: 1.0, 0.9 and 0.8 of the transmitted flux, calculated for three wall reflectivities: 1.0, 0.9 and 0.8 |
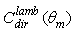 calculated from Eq. (11) is reported in Fig. 8.
calculated from Eq. (11) is reported in Fig. 8.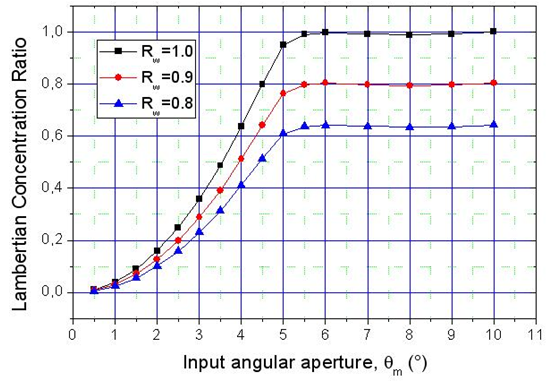 | Figure 8. Direct lambertian concentration ratio, 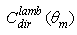 calculated for three wall reflectivities: calculated for three wall reflectivities: 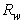 = 1.0, 0.9 and 0.8 = 1.0, 0.9 and 0.8 |
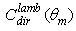 is always ≤1, that is the average output radiance is always smaller than the input radiance, being equal to it only when the internal wall is an ideal mirror and the input angular aperture is greater than the acceptance angle of the CPC (5°). This can be easily demonstrated considering that, for
is always ≤1, that is the average output radiance is always smaller than the input radiance, being equal to it only when the internal wall is an ideal mirror and the input angular aperture is greater than the acceptance angle of the CPC (5°). This can be easily demonstrated considering that, for 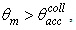 we have:
we have: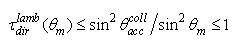 | (12) |

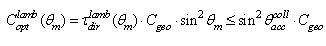
 (11’)Considering that
(11’)Considering that 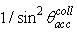 corresponds to the maximum value of the optical concentration ratio, equal to
corresponds to the maximum value of the optical concentration ratio, equal to 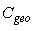 [1], from Eq. (11’) we conclude that
[1], from Eq. (11’) we conclude that 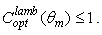
3.4. Analysis of the Flux Distribution on the Receiver
- To study the flux transmitted to the exit aperture of the CPC, the exit aperture was closed by an ideal absorber. Fig. 9 shows the maps of the irradiance on the receiver as function of the angular aperture of the lambertian beam at input, from 1.0° to 6.0°; the wall reflectivity is 1.0. Contrary to the maps obtained by irradiating the CPC with a parallel beam [2], the maps of Fig. 9 are symmetric respect to the optical axis, as consequence of the rotational symmetry of both the CPC and the lambertian beam. The optical simulations were performed by setting a number of input rays
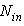 =100k for
=100k for 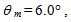 then
then 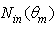 is given by:
is given by: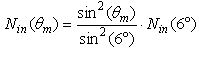 | (13) |
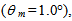 then it is distributed in the central part
then it is distributed in the central part 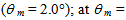
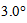 the center is impoverished, but again, starting from
the center is impoverished, but again, starting from 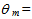
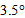 we have an almost uniform distribution of the flux in the central part of the receiver, which extends to the edge at increasing
we have an almost uniform distribution of the flux in the central part of the receiver, which extends to the edge at increasing 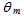 , to become uniform when
, to become uniform when 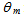 reaches a value equal to the acceptance angle (5°). Then we can say that the flow affects at first the central part of the receiver and then the outer ring. In essence, the less inclined rays gather in the central part of the receiver, while those more inclined gather on its edge.We can see from Fig. 10a, where the wall reflectivity is unitary and we have no optical losses inside the CPC, that the output irradiance profile becomes flat as soon as the angular aperture
reaches a value equal to the acceptance angle (5°). Then we can say that the flow affects at first the central part of the receiver and then the outer ring. In essence, the less inclined rays gather in the central part of the receiver, while those more inclined gather on its edge.We can see from Fig. 10a, where the wall reflectivity is unitary and we have no optical losses inside the CPC, that the output irradiance profile becomes flat as soon as the angular aperture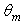 exceeds the acceptance angle (5.0°). By reducing
exceeds the acceptance angle (5.0°). By reducing 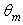 the irradiance profiles are slightly smoothed, because of the optical loss inside the CPC; at the same time, they become blunt at the edges, because the optical loss is higher there as an effect of the higher number of reflections, as we will see shortly after.
the irradiance profiles are slightly smoothed, because of the optical loss inside the CPC; at the same time, they become blunt at the edges, because the optical loss is higher there as an effect of the higher number of reflections, as we will see shortly after.  | Figure 10. Irradiance profiles of the flux at output of the CPC, irradiated by a lambertian beam of different angular apertures  Wall reflectivity: Wall reflectivity:  |
3.5. Average Number of Reflections of Locally Absorbed Rays
- As done for the total flux transmitted to the receiver, we are able now to evaluate the average number of reflections experienced by the rays reaching a specific point on the receiver. We use therefore the same Eq. (9), to be applied to the irradiance profiles of transmitted flux, calculated for different values of the wall reflectivity. The irradiance is expressed as:
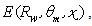 where x is the relative distance from the optical axis of the point on the receiver. The average number of reflections
where x is the relative distance from the optical axis of the point on the receiver. The average number of reflections 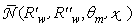 calculated for a specific value of
calculated for a specific value of 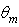 can be therefore obtained from two simulations taken at different wall reflectivities, as follows:
can be therefore obtained from two simulations taken at different wall reflectivities, as follows: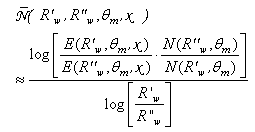 | (14) |
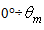 interval, experience before reaching a point on the receiver. As we are interested to know the average number of reflections done by the rays inclined in a narrow range
interval, experience before reaching a point on the receiver. As we are interested to know the average number of reflections done by the rays inclined in a narrow range 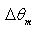 centered at a particular
centered at a particular 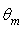 value, we have calculated new irradiance profiles,
value, we have calculated new irradiance profiles, 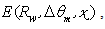 obtained as:
obtained as: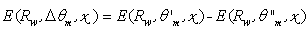 | (15) |
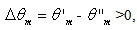 and from these profiles we have obtained the searched result:
and from these profiles we have obtained the searched result: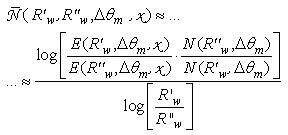 | (16) |
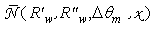 calculated for the five angular intervals:
calculated for the five angular intervals: 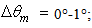
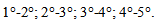 The curves have a very interesting behavior. First of all, they overlap quite well, showing that the number of reflections of rays reaching a specific point at distance x, is only slightly dependent on the angular divergence at input. This is particularly true for middle values of x, less for the points at the center and at the edge of the receiver. The second consideration to do is that
The curves have a very interesting behavior. First of all, they overlap quite well, showing that the number of reflections of rays reaching a specific point at distance x, is only slightly dependent on the angular divergence at input. This is particularly true for middle values of x, less for the points at the center and at the edge of the receiver. The second consideration to do is that 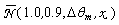 is low at the center of the receiver, between about 1 and 2, and grows moving towards the edges, reaching values between about 3 and 5. This explains the statement made at the end of section 3.4.As
is low at the center of the receiver, between about 1 and 2, and grows moving towards the edges, reaching values between about 3 and 5. This explains the statement made at the end of section 3.4.As 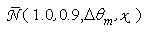 is not too much dependent on
is not too much dependent on 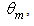 it is interesting to calculate its average respect to the different angular aperture intervals
it is interesting to calculate its average respect to the different angular aperture intervals 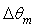 . The average quantity
. The average quantity 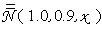 is shown in Fig. 12 (black curve). It is a very smooth curve, no longer containing the strong oscillations of the curves of Fig. 11.
is shown in Fig. 12 (black curve). It is a very smooth curve, no longer containing the strong oscillations of the curves of Fig. 11. 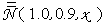 is well fitted by the fourth degree polynomial (see red curve in Fig. 12):
is well fitted by the fourth degree polynomial (see red curve in Fig. 12):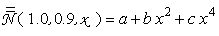 | (17) |
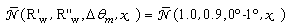 simulated for an angular aperture of the lambertian beam equal to 1°. The curve shows that
simulated for an angular aperture of the lambertian beam equal to 1°. The curve shows that 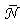 is exactly 1.0 in the central part of the receiver and increases with a step-like behavior moving towards the edge of the receiver, where the rays arrive after exactly 5 reflections. The rays at input are almost parallel to the optical axis, then the black curve of Fig. 13 is very similar to the red curve obtained in [2] when a collimated beam parallel to the optical axis irradiates the CPC. The difference between the two curves is very little: the red curve has a slightly larger zone with one reflection, and the number of reflections for the rays on the edge is now seven.
is exactly 1.0 in the central part of the receiver and increases with a step-like behavior moving towards the edge of the receiver, where the rays arrive after exactly 5 reflections. The rays at input are almost parallel to the optical axis, then the black curve of Fig. 13 is very similar to the red curve obtained in [2] when a collimated beam parallel to the optical axis irradiates the CPC. The difference between the two curves is very little: the red curve has a slightly larger zone with one reflection, and the number of reflections for the rays on the edge is now seven. 3.6. Angular Divergence of the Transmitted Rays
- The study of the angular divergence of rays at output of the CPC is important to optimize the absorption properties of the receiver. In the practical use of a PV solar concentrator, for example, the receiver is not an ideal absorber, but a solar cell with specific reflectance properties, that affect its light absorption capabilities in relation to the divergence of the incoming rays [20]. The flux absorbed by the solar cell can be expressed as:
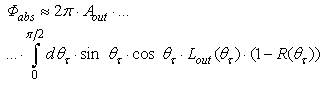 | (18) |
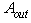 is the area of the cell,
is the area of the cell, 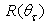 is the angle-resolved reflectance and
is the angle-resolved reflectance and 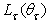 is the radiance of light transmitted at exit angle
is the radiance of light transmitted at exit angle 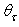 by the CPC (the radiance is not function of the azimuthal angle
by the CPC (the radiance is not function of the azimuthal angle 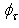 because the system input beam + CPC is rotationally symmetric). In Eq. (18), in general
because the system input beam + CPC is rotationally symmetric). In Eq. (18), in general 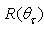 grows with
grows with 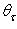 [20], then it is desirable that
[20], then it is desirable that 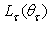 be not too high for high
be not too high for high 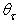 values. To check the angular distribution of radiance of light at the CPC receiver, we have irradiated the ideal CPC (
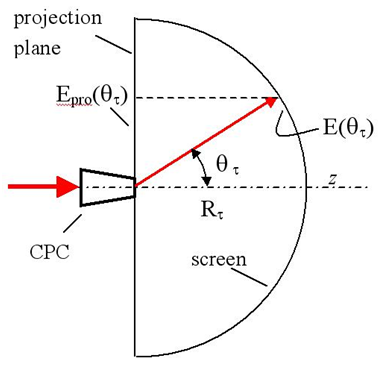
values. To check the angular distribution of radiance of light at the CPC receiver, we have irradiated the ideal CPC (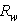 = 1.0) by a lambertian beam with different values of the angular aperture
= 1.0) by a lambertian beam with different values of the angular aperture 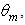 and the output flux has been collected by a hemispherical absorber (radius
and the output flux has been collected by a hemispherical absorber (radius 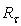 = 200 mm) centered on the receiver (see Fig. 14). The rotationally symmetric map of the flux density on the internal screen surface, projected on a plane orthogonal to the optical axis (see Fig. 16) and the corresponding radial profile, simulated at
= 200 mm) centered on the receiver (see Fig. 14). The rotationally symmetric map of the flux density on the internal screen surface, projected on a plane orthogonal to the optical axis (see Fig. 16) and the corresponding radial profile, simulated at 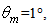 are shown in Fig. 15.
are shown in Fig. 15. 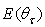 (W/m2) is the irradiance on the screen surface,
(W/m2) is the irradiance on the screen surface, 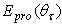 (W/m2) is its projection on the orthogonal plane and
(W/m2) is its projection on the orthogonal plane and 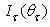 (W/sr) is the radiant intensity, the radiance
(W/sr) is the radiant intensity, the radiance 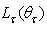 (W/m2sr) of the transmitted light becomes:
(W/m2sr) of the transmitted light becomes: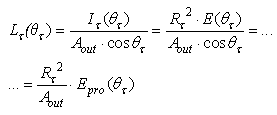 | (19) |
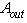 is the area of the output aperture of the CPC and
is the area of the output aperture of the CPC and 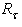 is the screen radius. From Eq. (19) we see that the profile of
is the screen radius. From Eq. (19) we see that the profile of 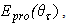 that reported in Fig. 15b, is the same of the radiance
that reported in Fig. 15b, is the same of the radiance 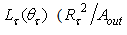 is a constant factor), and then the flux map of Fig. 15 is qualitatively the map of the transmitted radiance. The profile of
is a constant factor), and then the flux map of Fig. 15 is qualitatively the map of the transmitted radiance. The profile of 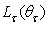 is worth of being analyzed in detail. Fig. 17 shows the effect of the angular divergence
is worth of being analyzed in detail. Fig. 17 shows the effect of the angular divergence 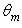 on the angular distribution of radiance of the transmitted beam, for a wall reflectivity
on the angular distribution of radiance of the transmitted beam, for a wall reflectivity 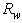 = 1.0 (no optical loss by absorption). The number of rays incident at input aperture are a function of
= 1.0 (no optical loss by absorption). The number of rays incident at input aperture are a function of 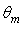 and follows the
and follows the 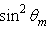 rule, which, in this case, corresponds to 50k at
rule, which, in this case, corresponds to 50k at 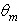 = 6°. The angular divergence
= 6°. The angular divergence 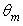 was varied from 1° to 10° with 1° steps, but we show in Fig. 17 only the first six diagrams, because the polar profiles of
was varied from 1° to 10° with 1° steps, but we show in Fig. 17 only the first six diagrams, because the polar profiles of 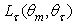 do not change significantly for
do not change significantly for 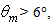 apart from small fluctuations at near
apart from small fluctuations at near 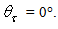 The radiance profiles show a strong central peak at
The radiance profiles show a strong central peak at 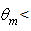
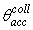 values. This peak is mainly produced by rays traveling close to the optical axis and crossing undisturbed the CPC without reflections on the internal wall. At
values. This peak is mainly produced by rays traveling close to the optical axis and crossing undisturbed the CPC without reflections on the internal wall. At 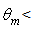
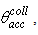 we find a “dead” zone large ≈ 15°, with no rays, followed by a large band of radiance extending from about 15° to 60°, that takes, near the acceptance angle, the characteristic shape of a “butterfly” or “dragonfly”. The “dead” zone is very similar to that occurring with irradiation by a collimated beam parallel to the optical axis [2]. In that work, we could explain that the dead zone upper limit (about 15°) was due to those rays impacting on the CPC wall at about 7 mm far from the axis, and coming out with a divergence of about 15°; this divergence is a lower limit, since away more from the axis, these rays undergo a second reflection that makes them diverge even more, and therefore makes it impossible exit angles of less than about 15°. Despite being the irradiation Lambertian, instead of parallel, this phenomenon is maintained, because the lambertian beam contains incoming parallel rays parallel or nearly parallel to the optical axis. When the input angular divergence
we find a “dead” zone large ≈ 15°, with no rays, followed by a large band of radiance extending from about 15° to 60°, that takes, near the acceptance angle, the characteristic shape of a “butterfly” or “dragonfly”. The “dead” zone is very similar to that occurring with irradiation by a collimated beam parallel to the optical axis [2]. In that work, we could explain that the dead zone upper limit (about 15°) was due to those rays impacting on the CPC wall at about 7 mm far from the axis, and coming out with a divergence of about 15°; this divergence is a lower limit, since away more from the axis, these rays undergo a second reflection that makes them diverge even more, and therefore makes it impossible exit angles of less than about 15°. Despite being the irradiation Lambertian, instead of parallel, this phenomenon is maintained, because the lambertian beam contains incoming parallel rays parallel or nearly parallel to the optical axis. When the input angular divergence 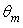 reaches the acceptance angle (5°), the radiance profile is quite flat up to 75° (the small fluctuations depend only on the limited number of incident rays) and keeps almost equal up to
reaches the acceptance angle (5°), the radiance profile is quite flat up to 75° (the small fluctuations depend only on the limited number of incident rays) and keeps almost equal up to 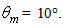 The same profile of transmitted radiance was achieved by increasing
The same profile of transmitted radiance was achieved by increasing 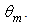 Fig. 18a shows, for example, the transmitted radiance profile obtained at
Fig. 18a shows, for example, the transmitted radiance profile obtained at 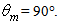 The simulation was carried out with a flux of 400k rays (400k W) and a processing time of about 12 hours; the number of rays, however, was less than would have been necessary to satisfy the
The simulation was carried out with a flux of 400k rays (400k W) and a processing time of about 12 hours; the number of rays, however, was less than would have been necessary to satisfy the 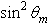 rule, which assures a constant radiance at input: ~ 4.5M rays and ~130 hours of processing time. The consequence is a loss in the signal-to-noise ratio, as it can be seen in Fig. 18a. Apart from the low signal-to-noise ratio, the simulation at
rule, which assures a constant radiance at input: ~ 4.5M rays and ~130 hours of processing time. The consequence is a loss in the signal-to-noise ratio, as it can be seen in Fig. 18a. Apart from the low signal-to-noise ratio, the simulation at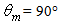 has not changed significantly the radiance profile found at 6° (see Fig. 17f) (we know in fact from [2], section 4.2, that input rays tilted more than ≈ 5.8° have no chances to reach the CPC exit opening): a quite flat profile at ~ 3.2·109 W/m2·sr from 0° to 75°, followed by a decay up to ~ 1.6·109 W/m2·sr at 90°. Despite not flat up to 90°, this is effectively the profile obtained with a lambertian beam. This was verified by irradiating the hemispherical screen directly with a lambertian beam, after removing the CPC. The result is the profile of Fig. 18b, where the intensity drops to 50% of maximum at the exit angle of 90°.The evolution of the radiance profiles as function of
has not changed significantly the radiance profile found at 6° (see Fig. 17f) (we know in fact from [2], section 4.2, that input rays tilted more than ≈ 5.8° have no chances to reach the CPC exit opening): a quite flat profile at ~ 3.2·109 W/m2·sr from 0° to 75°, followed by a decay up to ~ 1.6·109 W/m2·sr at 90°. Despite not flat up to 90°, this is effectively the profile obtained with a lambertian beam. This was verified by irradiating the hemispherical screen directly with a lambertian beam, after removing the CPC. The result is the profile of Fig. 18b, where the intensity drops to 50% of maximum at the exit angle of 90°.The evolution of the radiance profiles as function of 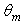 can be followed also transforming the radiance polar diagrams of Fig. 17 into Cartesian diagrams and overlapping them (see Fig. 19). I added also the
can be followed also transforming the radiance polar diagrams of Fig. 17 into Cartesian diagrams and overlapping them (see Fig. 19). I added also the 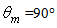 profile obtained at a reduced processing time (~11 times), distinguishable for the low signal-to-noise ratio. Apart from the radiance peak near
profile obtained at a reduced processing time (~11 times), distinguishable for the low signal-to-noise ratio. Apart from the radiance peak near 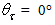 that we have already discussed, we see that the radiance profile monotonically grows in the
that we have already discussed, we see that the radiance profile monotonically grows in the 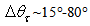 interval at increasing
interval at increasing 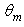 from 1° to 4°. A significant change in the radiance profile happens in the
from 1° to 4°. A significant change in the radiance profile happens in the 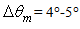 interval, where we observe the filling of the dead zone at low
interval, where we observe the filling of the dead zone at low 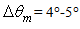 values, as well as of the region between ~20° and ~75°; the 75°-90° interval remains unfilled as explained before.
values, as well as of the region between ~20° and ~75°; the 75°-90° interval remains unfilled as explained before.3.7. Average Number of Reflections of Transmitted Rays
- We have previously analyzed the number of reflections made by the transmitted rays as function of
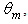 both as an average on the total flux, and as function on the distance, from the optical axis, of the impact point on the receiver. Now we look at the average number of reflections made by rays transmitted as function of the exit angle
both as an average on the total flux, and as function on the distance, from the optical axis, of the impact point on the receiver. Now we look at the average number of reflections made by rays transmitted as function of the exit angle 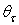 from the CPC, at different values of the input lambertian divergence
from the CPC, at different values of the input lambertian divergence 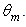 For this purpose, we have repeated the simulations of radiance shown in Fig. 17 with a different wall reflectance,
For this purpose, we have repeated the simulations of radiance shown in Fig. 17 with a different wall reflectance, 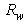 = 0.9. The average number of reflections was obtained by applying the following equation, with
= 0.9. The average number of reflections was obtained by applying the following equation, with 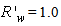 and
and 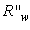 = 0.9:
= 0.9: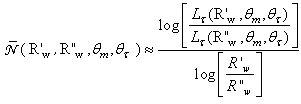 | (20) |
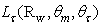 is the radiance of the flux transmitted at angle
is the radiance of the flux transmitted at angle 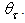 The numbers of output rays do not appear as they were the same at the two wall reflectivities. Fig. 20 shows the polar distribution of
The numbers of output rays do not appear as they were the same at the two wall reflectivities. Fig. 20 shows the polar distribution of 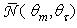 for angular divergence values
for angular divergence values 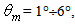 with 1° steps. There are many interesting features of the polar diagrams of
with 1° steps. There are many interesting features of the polar diagrams of 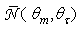 to highlight. First of all they are completely developed at
to highlight. First of all they are completely developed at 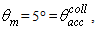 as it was for the radiance maps (Fig. 17). Then we notice that
as it was for the radiance maps (Fig. 17). Then we notice that 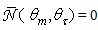 for exit rays close to the optical axis
for exit rays close to the optical axis 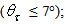 these rays do not touch the CPC wall. Then, from
these rays do not touch the CPC wall. Then, from 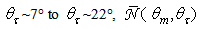 is exactly 1. At higher values of
is exactly 1. At higher values of 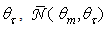 grows forming a lobo centered at ~45°, which is narrow at low
grows forming a lobo centered at ~45°, which is narrow at low 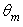 values, with a peak at
values, with a peak at 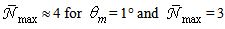 for
for 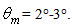 The lobo then widens occupying the whole range from ~45° to 90°. At
The lobo then widens occupying the whole range from ~45° to 90°. At 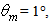 the rays exit the CPC at
the rays exit the CPC at 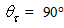 after one reflection; by increasing
after one reflection; by increasing 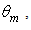 the reflections increase up to 2.75. One last consideration to do is about the value of
the reflections increase up to 2.75. One last consideration to do is about the value of 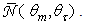 Whereas the number of reflections of a ray must be exactly an integer, this rarely happens to a mixture of rays, because they have not the same characteristics (same distance x at input aperture and same
Whereas the number of reflections of a ray must be exactly an integer, this rarely happens to a mixture of rays, because they have not the same characteristics (same distance x at input aperture and same 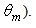 Exceptions are
Exceptions are 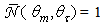 at all
at all 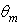 when
when 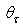 ~7°÷22° (see Figs. 20a-f), or at
~7°÷22° (see Figs. 20a-f), or at 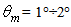 when
when 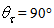 (see Figs. 20a,b), or again
(see Figs. 20a,b), or again 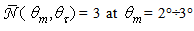 when
when 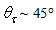 (see Figs. 20b,c). The diagrams of radiance of Fig. 17 and those of the average number of reflections of Fig. 20 do not clarify, therefore, what are, at the origin, the rays causing a particular radiance or number of reflections profile.
(see Figs. 20b,c). The diagrams of radiance of Fig. 17 and those of the average number of reflections of Fig. 20 do not clarify, therefore, what are, at the origin, the rays causing a particular radiance or number of reflections profile.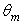 interval (0°-5°) in five smaller intervals
interval (0°-5°) in five smaller intervals 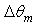 = (0°-1°); (1°-2°); (2°-3°); (3°-4°); (4°-5°), with
= (0°-1°); (1°-2°); (2°-3°); (3°-4°); (4°-5°), with 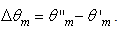 The formula used to calculate the number of reflections is:
The formula used to calculate the number of reflections is: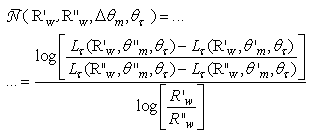 | (21) |
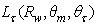 are those previously simulated with
are those previously simulated with 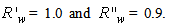 Eq. (21) only requires subtraction of radiance profiles with different
Eq. (21) only requires subtraction of radiance profiles with different 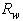 values. The obtained profiles of
values. The obtained profiles of 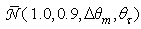 are reported, in Cartesian representation, in Fig. 21, which allows to distinguish better the transmitted rays. Fig. 21 confirms that
are reported, in Cartesian representation, in Fig. 21, which allows to distinguish better the transmitted rays. Fig. 21 confirms that 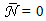 for
for 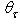 <7.5° and that
<7.5° and that 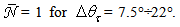 We note also that the various
We note also that the various 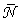 profiles consist of bands with the maximum on integer values of
profiles consist of bands with the maximum on integer values of 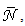 as desired. The position of these bands
as desired. The position of these bands 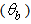 and their maximum value
and their maximum value 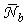 are reported in Tab. 1, as function of
are reported in Tab. 1, as function of 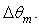
|
4. Analysis of the Reflected Flux
4.1. Optical Reflection Efficiency
- Let us consider at first the total reflected flux:
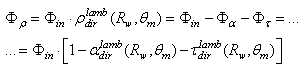 | (22) |
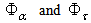 are the total absorbed and transmitted fluxes, respectively, and
are the total absorbed and transmitted fluxes, respectively, and 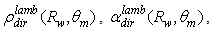
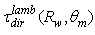 are the lambertian reflection, absorption and transmission efficiencies, respectively. The total reflected flux can be expressed as function of the radiance
are the lambertian reflection, absorption and transmission efficiencies, respectively. The total reflected flux can be expressed as function of the radiance 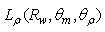 of the reflected light:
of the reflected light: 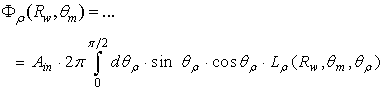 | (23) |
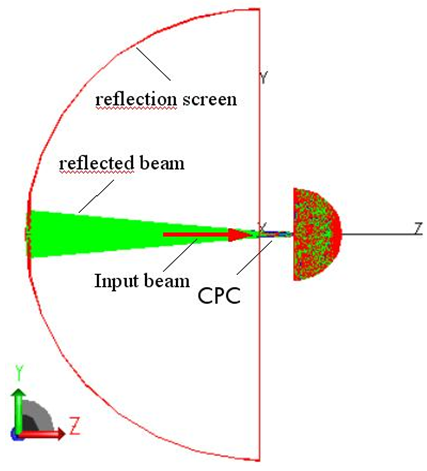
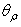 is the polar angle of the reflected ray. To simulate the reflection properties of the CPC, we have adopted a scheme similar to that used to measure the transmitted light (see Figs. 14, 16), adding a hemispherical screen with
is the polar angle of the reflected ray. To simulate the reflection properties of the CPC, we have adopted a scheme similar to that used to measure the transmitted light (see Figs. 14, 16), adding a hemispherical screen with 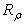 = 1000 mm radius and ideal absorbance, able to gather all the reflected light from the CPC. The CPC protrudes out of the screen and the center of input aperture meets that of the screen (see Fig. 22).
= 1000 mm radius and ideal absorbance, able to gather all the reflected light from the CPC. The CPC protrudes out of the screen and the center of input aperture meets that of the screen (see Fig. 22).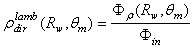 | (24) |
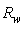 = 1.0 (black curve), condition for which
= 1.0 (black curve), condition for which 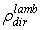 is equal to the ratio between the number of the back-reflected rays to the input rays, because of the absence of optical loss inside the CPC. The reflection efficiency is zero below the acceptance angle, as all the rays are transmitted; then it appears in correspondence of
is equal to the ratio between the number of the back-reflected rays to the input rays, because of the absence of optical loss inside the CPC. The reflection efficiency is zero below the acceptance angle, as all the rays are transmitted; then it appears in correspondence of 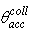 (see red curve).
(see red curve). | Figure 23. Lambertian reflection efficiency 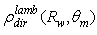 of the 3D-CPC calculated for of the 3D-CPC calculated for 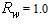 and 0.9 wall reflectivity. A portion of the curve of and 0.9 wall reflectivity. A portion of the curve of 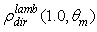 is also shown vs. is also shown vs. 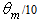 (x axis scaled by a factor of 10) (x axis scaled by a factor of 10) |
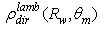 for
for 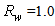 is easily obtained considering that it is simply the complement to 1 of the transmission efficiency
is easily obtained considering that it is simply the complement to 1 of the transmission efficiency 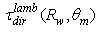 when
when 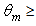
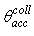 (see Eq. (7)). We have therefore:
(see Eq. (7)). We have therefore: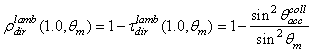 | (25) |
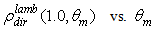 is quite different from that of
is quite different from that of 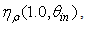 the reflection efficiency relative to a parallel beam [2]; in that case it was growing rapidly before the acceptance angle, reaching half of its maximum just in correspondence of it. With a lambertian beam,
the reflection efficiency relative to a parallel beam [2]; in that case it was growing rapidly before the acceptance angle, reaching half of its maximum just in correspondence of it. With a lambertian beam, 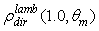 is growing more slowly (see Fig. 23) because a part of the beam, that corresponding to
is growing more slowly (see Fig. 23) because a part of the beam, that corresponding to 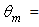
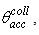 is always transmitted. From Eq. (25) we see that the limit of
is always transmitted. From Eq. (25) we see that the limit of 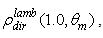 for
for 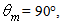 is:
is: 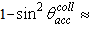
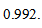 The reflection efficiency data relative to
The reflection efficiency data relative to 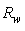 = 0.9 are shown in Fig. 23 (blue curve). While the curve of
= 0.9 are shown in Fig. 23 (blue curve). While the curve of 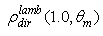 is always growing, the curve of
is always growing, the curve of 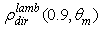 reaches a maximum at
reaches a maximum at 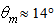 and then decreases down to 16% for
and then decreases down to 16% for 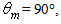 being strongly limited by the absorbance of light on the CPC wall.
being strongly limited by the absorbance of light on the CPC wall.4.2. Angular Divergence of the Reflected Rays
- The study of the angular divergence of back reflected rays from input aperture has not a practical relevance as it has in the case of the transmitted rays, but it is a useful exercise to apply also to the back reflected rays concepts of the theory of solar concentrators. To simplify the discussion, we limit ourselves to consider an ideal CPC
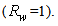 As already seen discussing the transmitted flux, the TracePro software produces on the collecting screen a flux map corresponding to the irradiance on the screen wall projected on a plane orthogonal to the z axis. Apart from a dimensional constant factor, equal to
As already seen discussing the transmitted flux, the TracePro software produces on the collecting screen a flux map corresponding to the irradiance on the screen wall projected on a plane orthogonal to the z axis. Apart from a dimensional constant factor, equal to 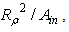 with
with 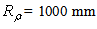 radius of the screen and
radius of the screen and 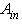 input aperture of the CPC, this map is equivalent to that of the radiance of light back reflected by the input aperture, as it has been demonstrated in Eq. (19) for the transmitted flux. The plot of these maps is not necessary, because they are symmetric with respect to the optical axis, and then they give the same information of the profiles of their cross sections.A Cartesian representation of the reflected radiance simulated for some values of
input aperture of the CPC, this map is equivalent to that of the radiance of light back reflected by the input aperture, as it has been demonstrated in Eq. (19) for the transmitted flux. The plot of these maps is not necessary, because they are symmetric with respect to the optical axis, and then they give the same information of the profiles of their cross sections.A Cartesian representation of the reflected radiance simulated for some values of 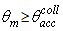 up to
up to 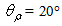 is shown in Fig. 24. The reflected radiance appears at
is shown in Fig. 24. The reflected radiance appears at 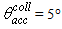 and then grows in intensity reaching a maximum of about 3.2x109 (W/m2sr) at around 12°. Keeping constant in intensity, the radiance band expands then in terms of angular divergence. The envelope of all profiles corresponds to the radiance profile at
and then grows in intensity reaching a maximum of about 3.2x109 (W/m2sr) at around 12°. Keeping constant in intensity, the radiance band expands then in terms of angular divergence. The envelope of all profiles corresponds to the radiance profile at 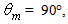 and is characterized by a depression in the center, caused by the “loss” by transmitted rays. This profile, if overturned, form a band of 3.2x109 (W/m2sr) intensity and a width FWHM ≈ 2 x 4.7°. This band definitely has to do with the missing transmitted rays, but it is unexpected that it is equal to ≈ 2 x 4.5° instead of being 2 x
and is characterized by a depression in the center, caused by the “loss” by transmitted rays. This profile, if overturned, form a band of 3.2x109 (W/m2sr) intensity and a width FWHM ≈ 2 x 4.7°. This band definitely has to do with the missing transmitted rays, but it is unexpected that it is equal to ≈ 2 x 4.5° instead of being 2 x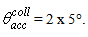
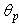 and their full width at half maximum
and their full width at half maximum 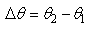 is reported as function of
is reported as function of 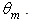 The evolution of
The evolution of 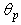 is perfectly linear and is defined by:
is perfectly linear and is defined by: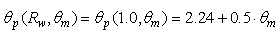 | (26) |
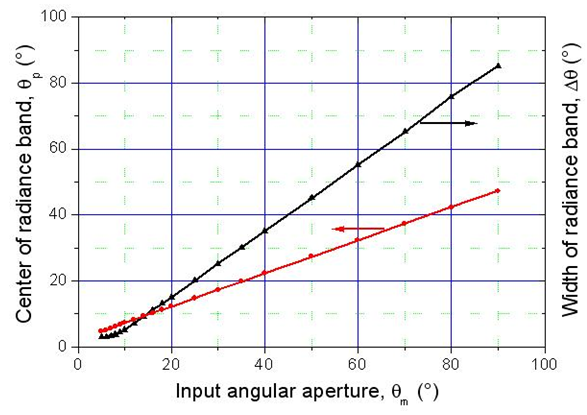 | Figure 25. Center of the radiance bands  and their full width at half maximum and their full width at half maximum  as function of as function of  |
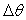 is different; after a slow rising up to 10°, the behavior becomes linear and is defined by the function:
is different; after a slow rising up to 10°, the behavior becomes linear and is defined by the function: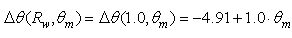 | (27) |
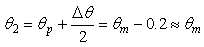 | (28) |
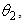 therefore, is almost equal to the maximum entrance angle,
therefore, is almost equal to the maximum entrance angle, 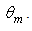 This result is a direct consequence of the Liouville theorem [6], establishing the invariance of the “generalized étendue”, the volume occupied by the system in the phase space, as expressed by Eq. (29) (see also Fig. 26):
This result is a direct consequence of the Liouville theorem [6], establishing the invariance of the “generalized étendue”, the volume occupied by the system in the phase space, as expressed by Eq. (29) (see also Fig. 26): 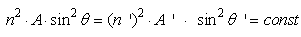 | (29) |
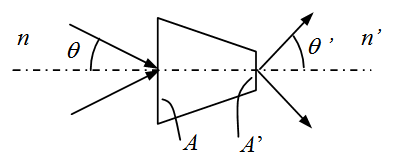 | Figure 26. Scheme of a generic concentrator with the three main parameters for the input and output apertures: index of refraction, area and angular divergence |
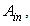 then we have:
then we have: 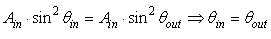 | (30) |
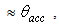 and an external wall with semi-opening equal to the angular aperture of the lambertian beam
and an external wall with semi-opening equal to the angular aperture of the lambertian beam 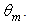 Cross sections of these beams are then rings with the inner circle growing, at increasing
Cross sections of these beams are then rings with the inner circle growing, at increasing 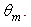 from 5° to 12°, and the outer circle from 5° to 90°.
from 5° to 12°, and the outer circle from 5° to 90°.4.3. Average Number of Reflections of the Total Reflected Rays
- To derive the average number of reflections of the total reflected flux,
 it is sufficient to analyze the lambertian reflectance
it is sufficient to analyze the lambertian reflectance 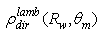 at two wall reflectivities and using the formula:
at two wall reflectivities and using the formula: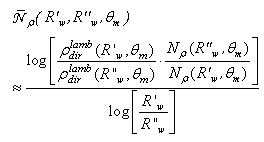 | (31) |
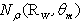 is the number of reflected rays collected by the screen. The reflection efficiency functions used are those calculated at
is the number of reflected rays collected by the screen. The reflection efficiency functions used are those calculated at 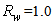 and
and 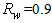 (see Fig. 23).Fig. 28 shows the curve of
(see Fig. 23).Fig. 28 shows the curve of 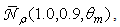 obtained applying Eq. (31) to the pair of reflectivities (1.0; 0.9). The average number of reflections is four at near the acceptance angle (5°) and then grows monotonically reaching up to 16 reflections for
obtained applying Eq. (31) to the pair of reflectivities (1.0; 0.9). The average number of reflections is four at near the acceptance angle (5°) and then grows monotonically reaching up to 16 reflections for 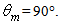
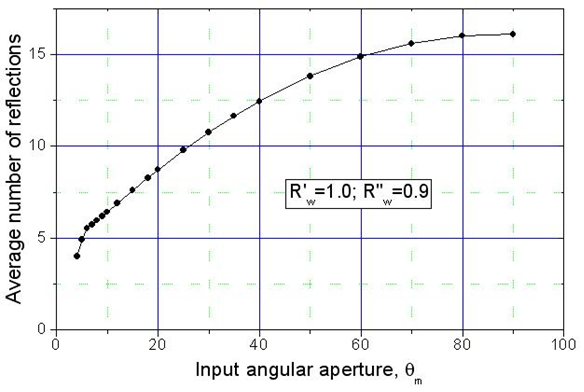 | Figure 28. Average number of internal reflections of the back reflected rays, simulated by applying Eq. (31) for the pair of values of internal wall reflectivity: 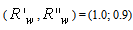 |
4.4. Average Number of Reflections Associated to the Reflected Radiance
- As we have done with the transmitted flux, the number of internal reflections of the reflected rays, as function of the exit angle
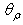 at different values of the angular aperture
at different values of the angular aperture 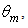 can be calculated by simulating the radiance shown in Fig. 27 with a different wall reflectance,
can be calculated by simulating the radiance shown in Fig. 27 with a different wall reflectance, 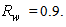 The average number of reflections
The average number of reflections 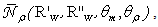 with
with 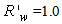 and
and 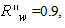 was obtained by applying the following equation:
was obtained by applying the following equation: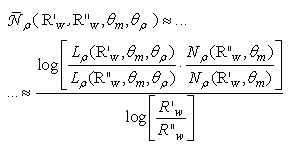 | (32) |
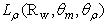 is the radiance of the flux reflected at
is the radiance of the flux reflected at 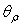 angle and
angle and 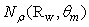 is the number of total reflected rays. The average number of internal reflections of the rays reflected at
is the number of total reflected rays. The average number of internal reflections of the rays reflected at 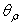 angle is shown in Fig. 29a for
angle is shown in Fig. 29a for 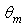 = 5°, 6°, 8°, 10°, 12°, 18°, 20°, and in Fig. 29b for
= 5°, 6°, 8°, 10°, 12°, 18°, 20°, and in Fig. 29b for 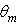 = 30°, 40°, 50°, 60°, 70°, 80°, 90°. It is interesting to note that, apart from the curve corresponding to
= 30°, 40°, 50°, 60°, 70°, 80°, 90°. It is interesting to note that, apart from the curve corresponding to 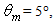 all other curves have a characteristic “V” shape with a minimum of
all other curves have a characteristic “V” shape with a minimum of 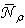 equal to ≈5 on the direction of the optical axis of the CPC, and a maximum of
equal to ≈5 on the direction of the optical axis of the CPC, and a maximum of 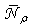 that grows at increasing
that grows at increasing 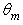 and falling approximately at
and falling approximately at 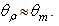 The results of Fig. 29 are very plausible: the higher the angular divergence of the incoming beam, the greater the number of reflections that the rays experience within the CPC, the greater the exit angle of the rays that make the maximum number of internal reflections. It is also interesting to note that, for exit angles
The results of Fig. 29 are very plausible: the higher the angular divergence of the incoming beam, the greater the number of reflections that the rays experience within the CPC, the greater the exit angle of the rays that make the maximum number of internal reflections. It is also interesting to note that, for exit angles 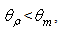 all the curves show an increasing trend of
all the curves show an increasing trend of 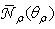 that is almost linear, particularly for high values of
that is almost linear, particularly for high values of 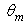 (see Fig. 29b). An exception to what has been said so far makes the curve corresponding to
(see Fig. 29b). An exception to what has been said so far makes the curve corresponding to 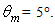 It shows a constant trend
It shows a constant trend 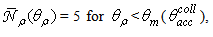 but then decreases with increasing of
but then decreases with increasing of 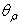 over the value of
over the value of 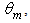 as do all the other curves. With regard to the values of
as do all the other curves. With regard to the values of 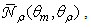 they range from about 5 to about 30 and grow at growing
they range from about 5 to about 30 and grow at growing 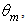 as illustrated in Fig. 28. Finally, Fig. 30 shows two examples of polar representation of
as illustrated in Fig. 28. Finally, Fig. 30 shows two examples of polar representation of 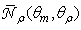 for
for 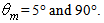
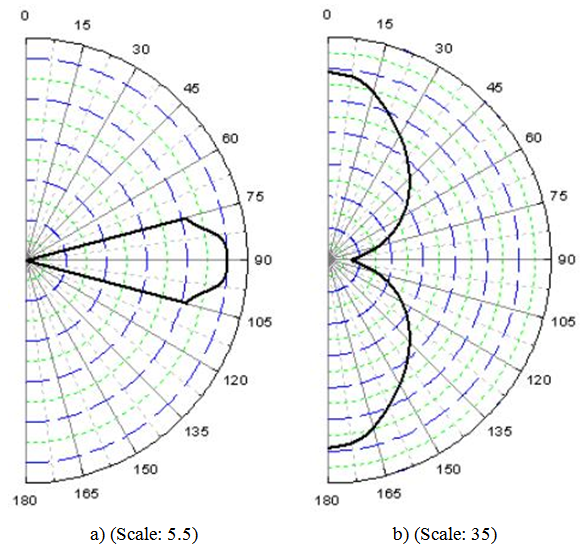 | Figure 30. Polar representation of 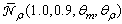 for for 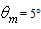 (a) and 90° (b) (a) and 90° (b) |
5. Analysis of the Absorbed Flux
5.1. Optical Absorption Efficiency
- From the data of transmission efficiency and reflection efficiency we immediately derive the “absorption efficiency” by the expression [1]:
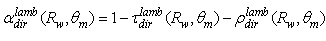 | (33) |
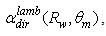 calculated for the wall reflectivities
calculated for the wall reflectivities 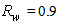 and 0.8, is shown in Fig. 31. The simulation with
and 0.8, is shown in Fig. 31. The simulation with 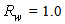 is useless in this case, as it would give a systematic zero absorption efficiency. For
is useless in this case, as it would give a systematic zero absorption efficiency. For 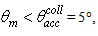 the absorption of light is due to the internal reflections of mainly the transmitted rays, these reflections being about 2, as we see in Fig. 6.
the absorption of light is due to the internal reflections of mainly the transmitted rays, these reflections being about 2, as we see in Fig. 6. 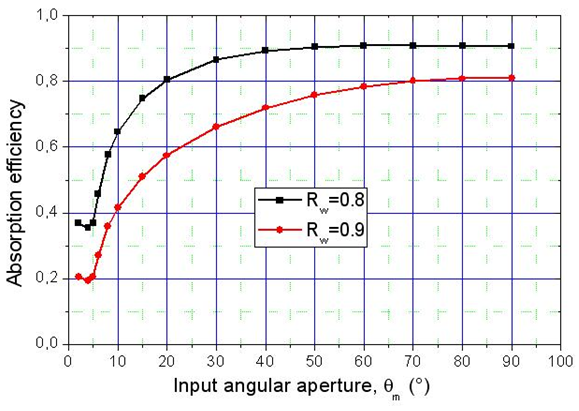 | Figure 31. Absorption efficiency 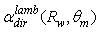 of the 3D-CPC calculated for two wall reflectivities: of the 3D-CPC calculated for two wall reflectivities: 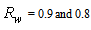 |
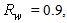 and ≈2x20% when
and ≈2x20% when 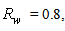 as it can be seen in Fig. 31. For
as it can be seen in Fig. 31. For 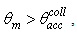 the absorption of light inside the CPC increases due to the contribution given by the back reflected rays, whose average number of internal reflections increases from 4 to 16 at increasing
the absorption of light inside the CPC increases due to the contribution given by the back reflected rays, whose average number of internal reflections increases from 4 to 16 at increasing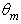 from 4° to 90° (see Fig. 28).
from 4° to 90° (see Fig. 28).5.2. Distribution of the Absorbed Flux
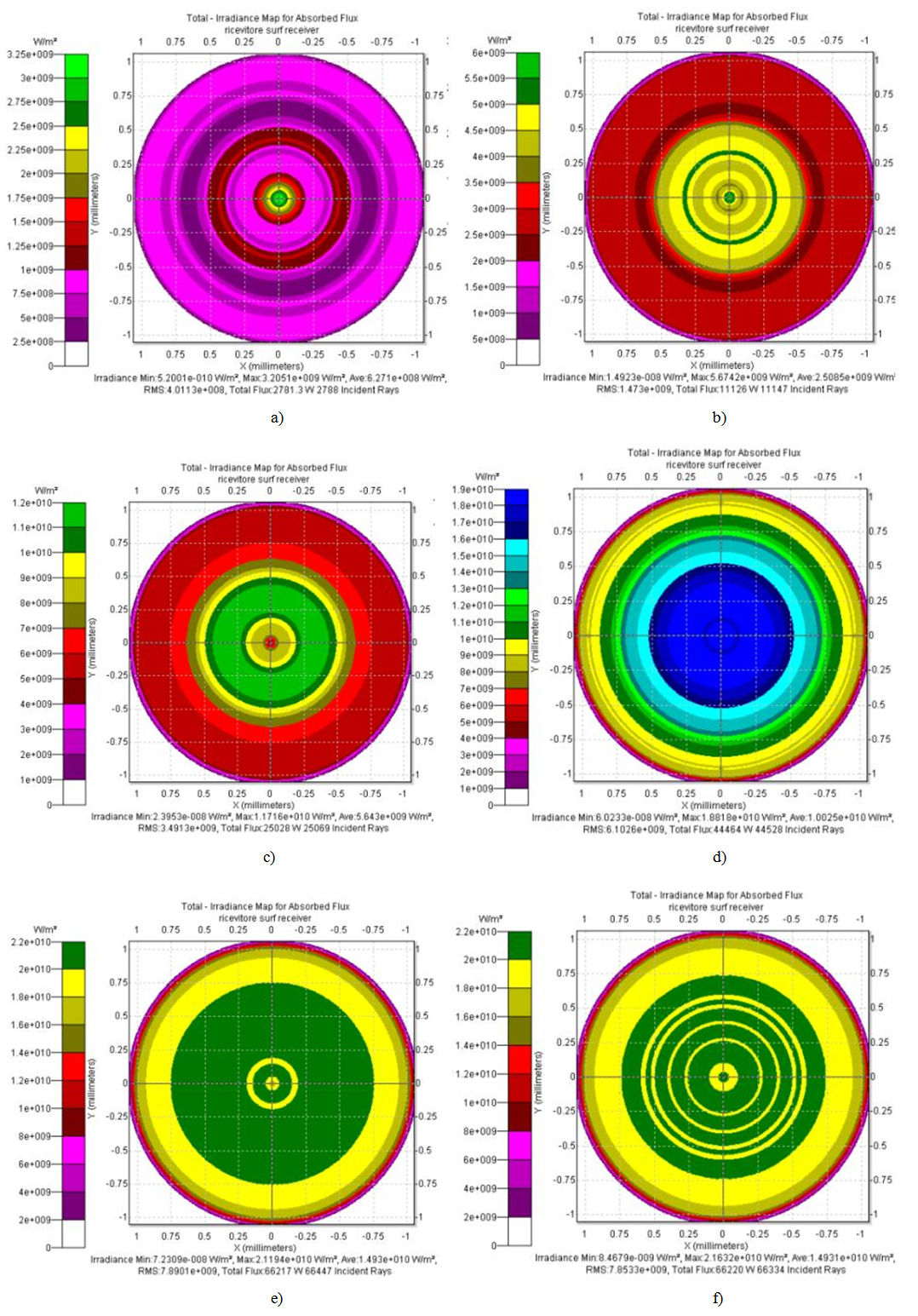
- Here we study how the absorbed flux is distributed inside the CPC. At this purpose a value of wall reflectivity
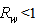 was selected. After each irradiation, by selecting the internal wall of the CPC, the simulation program produces a map of the absorbed flux, projected on the x/y plane orthogonal to the optical axis z. In this way, the map is an annulus with outer radius that of input aperture, a = 12.035 mm, and with inner radius that of output aperture, a’ = 1.052 mm (see Section 2). The intensity map is the projection on the x/y plane of the absorbed irradiation (in W/m2). Some maps of the absorbed flux are shown in Fig. 32 for the wall reflectivity
was selected. After each irradiation, by selecting the internal wall of the CPC, the simulation program produces a map of the absorbed flux, projected on the x/y plane orthogonal to the optical axis z. In this way, the map is an annulus with outer radius that of input aperture, a = 12.035 mm, and with inner radius that of output aperture, a’ = 1.052 mm (see Section 2). The intensity map is the projection on the x/y plane of the absorbed irradiation (in W/m2). Some maps of the absorbed flux are shown in Fig. 32 for the wall reflectivity 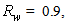 a typical value for realistic solar concentrators. The angular aperture of the lambertian beam has been varied from 10° to 90°. From Fig. 32 we can see that the flux density on the wall progressively moves from the exit to the input aperture, and, starting from 60°, the region adjacent to the exit opening is completely devoid of flux.
a typical value for realistic solar concentrators. The angular aperture of the lambertian beam has been varied from 10° to 90°. From Fig. 32 we can see that the flux density on the wall progressively moves from the exit to the input aperture, and, starting from 60°, the region adjacent to the exit opening is completely devoid of flux. to remove the projection operation made by the program, where α is the angle that the tangent to the CPC profile makes with the optical axis, given by [2]:
to remove the projection operation made by the program, where α is the angle that the tangent to the CPC profile makes with the optical axis, given by [2]: 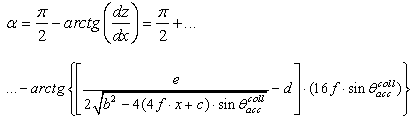 | (34) |
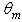 values, the flux is restricted in a thin zone near the exit opening, with the peak of irradiance increasing and moving towards higher z values at increasing
values, the flux is restricted in a thin zone near the exit opening, with the peak of irradiance increasing and moving towards higher z values at increasing 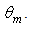 For
For 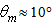 a large band appears in proximity of the input opening and increases at increasing
a large band appears in proximity of the input opening and increases at increasing 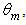 remaining centered at about z = 115 mm and leaving a hollow in the center of the CPC. A similar result was observed with parallel beams at input increasing the incidence angle from
remaining centered at about z = 115 mm and leaving a hollow in the center of the CPC. A similar result was observed with parallel beams at input increasing the incidence angle from 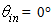 to
to 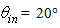 [2]. For
[2]. For 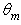 values higher than ≈ 30°, this band becomes dominant and most of the flux is absorbed near the input opening (see Fig. 33b). The effect of the increase of the angular divergence of the input beam is ultimately to move much of the flux to the input, as it has been anticipated by the maps of Fig. 32.
values higher than ≈ 30°, this band becomes dominant and most of the flux is absorbed near the input opening (see Fig. 33b). The effect of the increase of the angular divergence of the input beam is ultimately to move much of the flux to the input, as it has been anticipated by the maps of Fig. 32.6. Conclusions
- In conclusion, we have presented the results of optical simulations performed on a 3D-CPC nonimaging concentrator, irradiated in direct mode by a lambertian beam. This simulation work is the second discussing the practical applications of the theoretical methods presented in the first part of the series. The “direct” mode of irradiation is here distinguished by the “inverse” mode of irradiation, which will be discussed in a forthcoming part of the series. In this work we analyze the optical properties of the 3D-CPC with canonical shape (no truncation), with an acceptance angle at collimated light of 5° and maximum exit angle of 90°. The CPC has been analyzed in extreme detail by using a ray-tracing program. We have explored its transmission properties, those of the most practical importance when the 3D-CPC is used in a solar system, in terms of transmission efficiency, spatial and angular distribution of the flux at the output. Generally of less importance is the study of its reflection and absorption properties. Nevertheless, we have dedicated a large part of this paper also to these aspects, applying the same methods used for the transmitted light, because it helps to understand the secret mechanism of light concentration in a CPC. In the previous work of this series, we have analyzed the optical properties of the CPC irradiated by a collimated beam, oriented at different polar angles respect to the optical axis. In the actual work, we have just modified the geometry of the input beam, using a lambertian beam, that is a beam with cylindrical symmetry and constant radiance. This allowed us to obtain cylindrically symmetric beams at output of the CPC, that have facilitated the elaboration of the results, and to introduce new optical quantities, some already defined in the first theoretical work, others defined for the first time in this work. As in this work we have dealt with the CPC as if it were a generic optical element, we believe it will help to introduce into the routine work of the optical design new methods of simulation to be applied universally to the optical devices.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML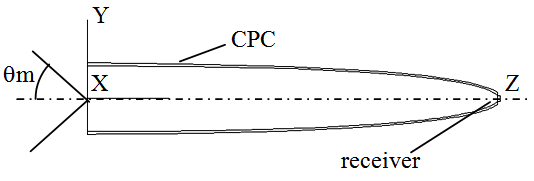
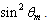 is the maximum angle of aperture of the input Lambertian beam. The angle of acceptance of a parallel beam is
is the maximum angle of aperture of the input Lambertian beam. The angle of acceptance of a parallel beam is 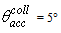
 = 1.0° (a); 2.0° (b); 3.0° (c); 4.0° (d); 5.0° (e); 6.0° (f). Number of input rays: 100k at
= 1.0° (a); 2.0° (b); 3.0° (c); 4.0° (d); 5.0° (e); 6.0° (f). Number of input rays: 100k at  = 6°.
= 6°.  = 1.0
= 1.0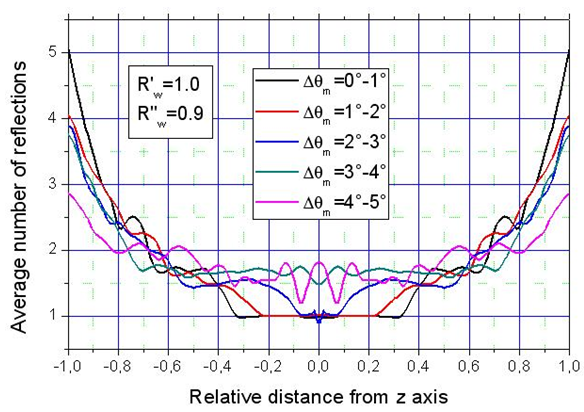
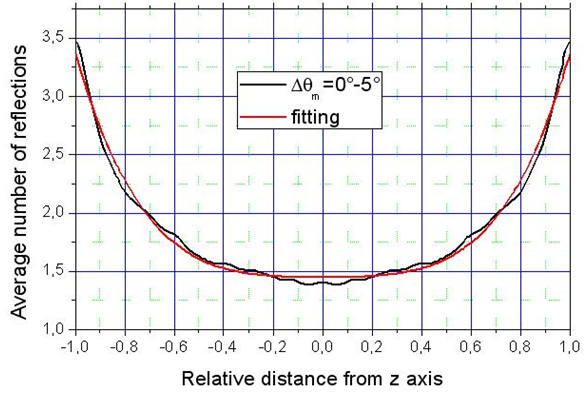
 = 0°-5° (black curve). The red curve is the fitting polynomial
= 0°-5° (black curve). The red curve is the fitting polynomial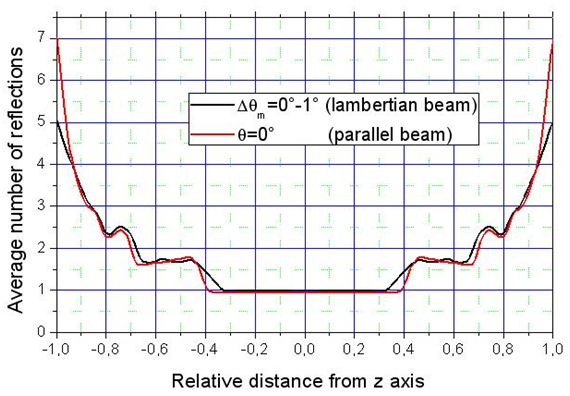
 = 0°-1° (black curve) and by a collimated beam parallel to the optical axis of the CPC (red curve)
= 0°-1° (black curve) and by a collimated beam parallel to the optical axis of the CPC (red curve)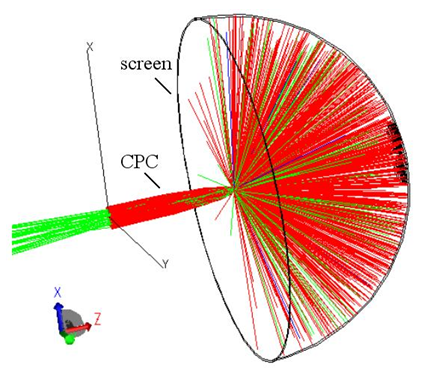
 The transmitted rays are collected by a hemispherical screen with a radius
The transmitted rays are collected by a hemispherical screen with a radius 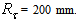 Some of rays (green color) are back reflected and attenuated because the wall reflectivity is
Some of rays (green color) are back reflected and attenuated because the wall reflectivity is  = 0.9. Most of rays are transmitted and impact on the spherical screen; the red rays are less attenuated (lower number of reflections inside the CPC), whereas the green rays are more attenuated (higher number of reflections inside the CPC)
= 0.9. Most of rays are transmitted and impact on the spherical screen; the red rays are less attenuated (lower number of reflections inside the CPC), whereas the green rays are more attenuated (higher number of reflections inside the CPC)
 ) produced on the screen, projected over a plane orthogonal to the optical axis. The input is a lambertian beam with
) produced on the screen, projected over a plane orthogonal to the optical axis. The input is a lambertian beam with 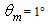
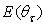 on its internal wall and the projection of this irradiance,
on its internal wall and the projection of this irradiance, 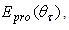 on a plane orthogonal to the optical axis
on a plane orthogonal to the optical axis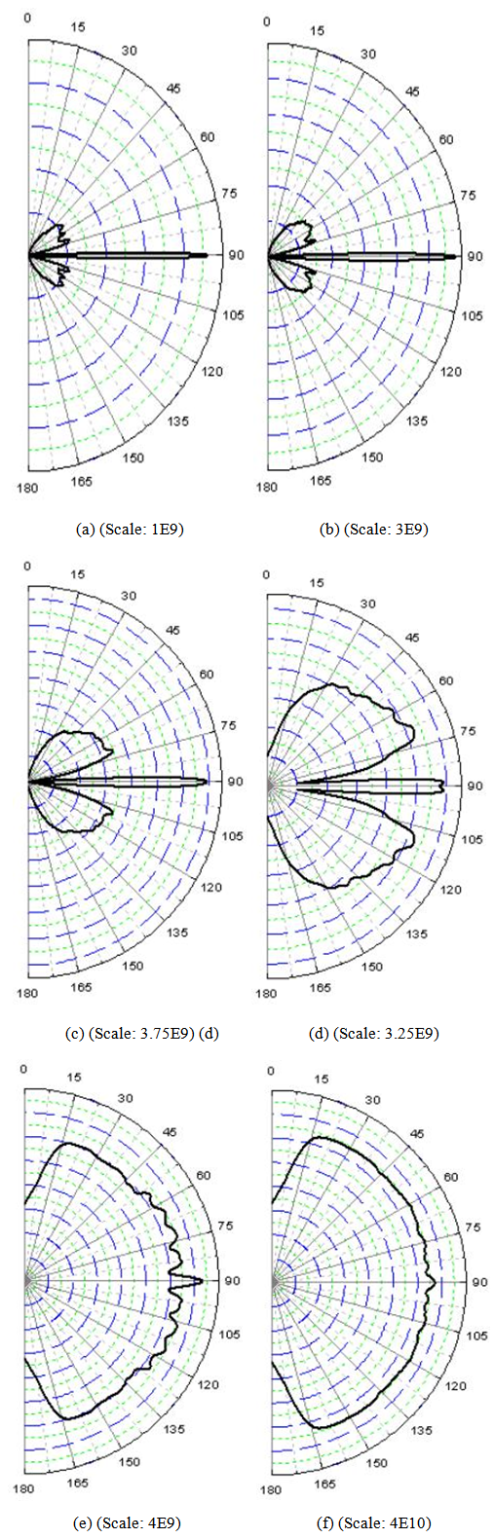
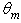 = 1° (a); 2° (b); 3° (c); 4° (d); 5° (e); 6° (f). For the angular divergence
= 1° (a); 2° (b); 3° (c); 4° (d); 5° (e); 6° (f). For the angular divergence 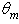 = 6° (f), We have used 500k rays at input, 10 times more than required to follow the
= 6° (f), We have used 500k rays at input, 10 times more than required to follow the 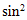
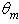 rule. The scale of radiance is expressed in
rule. The scale of radiance is expressed in 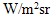 and is reported near each figure. The wall reflectivity is constant and equal to 1.0
and is reported near each figure. The wall reflectivity is constant and equal to 1.0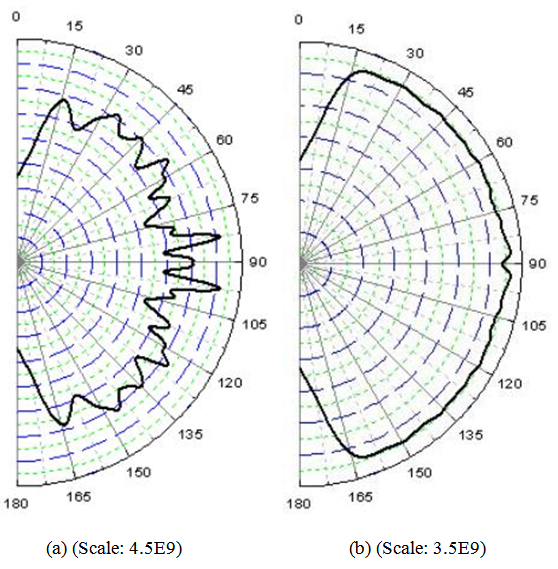
 = 90°, 400k rays at input, ~ 11 times less than required to follow the
= 90°, 400k rays at input, ~ 11 times less than required to follow the 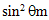 rule. (b) Angular divergence
rule. (b) Angular divergence  = 90°, 500k rays projected on the hemispherical screen directly, without the presence of the CPC. The wall reflectivity is 1.0. The scale of radiance is expressed in
= 90°, 500k rays projected on the hemispherical screen directly, without the presence of the CPC. The wall reflectivity is 1.0. The scale of radiance is expressed in 
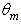 =1°; 2°; 3°; 4°; 5°; 6°; 90°. The wall reflectance is constant and equal to 1.0
=1°; 2°; 3°; 4°; 5°; 6°; 90°. The wall reflectance is constant and equal to 1.0
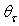 at different values of the lambertian angular divergence
at different values of the lambertian angular divergence  : 1° (a); 2° (b); 3° (c); 4° (d); 5° (e); 6° (f)
: 1° (a); 2° (b); 3° (c); 4° (d); 5° (e); 6° (f)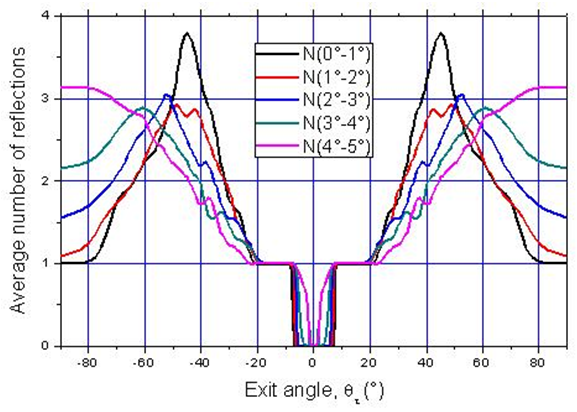
 =(0°-1°) (black); (1°-2°) (red); (2°-3°) (blue); (3°-4°) (dark cyan); (4°-5°) (magenta)
=(0°-1°) (black); (1°-2°) (red); (2°-3°) (blue); (3°-4°) (dark cyan); (4°-5°) (magenta) profiles. The bands
profiles. The bands  with angular position
with angular position 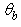 are reported as function of the
are reported as function of the 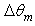 interval
interval
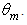 The reflected flux is measured by an absorbing hemispherical screen of radius
The reflected flux is measured by an absorbing hemispherical screen of radius  = 1000 mm. The CPC of the figure is not ideal (
= 1000 mm. The CPC of the figure is not ideal ( = 0.9), as consequence, the incident rays (red color) are attenuated after reflection (green color). The output of the CPC has been left open, so the transmitted rays are visible. Most of the transmitted rays are attenuated (green color); the red beam on the z-axis is made of rays crossing undisturbed the CPC
= 0.9), as consequence, the incident rays (red color) are attenuated after reflection (green color). The output of the CPC has been left open, so the transmitted rays are visible. Most of the transmitted rays are attenuated (green color); the red beam on the z-axis is made of rays crossing undisturbed the CPC
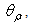 simulated for some values of
simulated for some values of 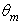 from 5° to 20°. The envelope profile gives a reversed band due to the loss by transmitted rays and its FWHM ≈ 2x 4.5°. The wall reflectivity is 1.0
from 5° to 20°. The envelope profile gives a reversed band due to the loss by transmitted rays and its FWHM ≈ 2x 4.5°. The wall reflectivity is 1.0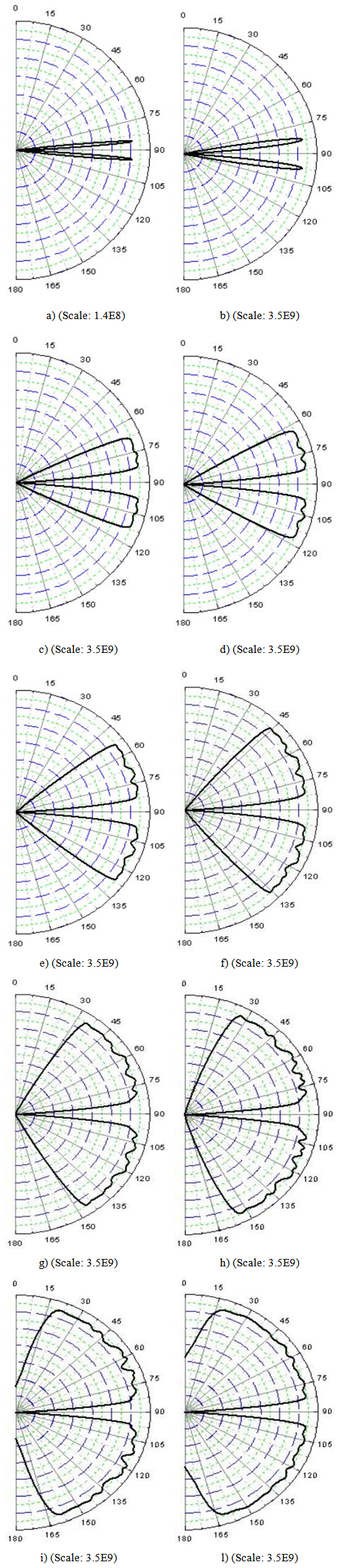
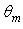 =5° (a); 10° (b); 20° (c); 30° (d); 40° (e); 50° (f); 60° (g); 70° (h); 80° (i); 90° (l). The scale of radiance is expressed in
=5° (a); 10° (b); 20° (c); 30° (d); 40° (e); 50° (f); 60° (g); 70° (h); 80° (i); 90° (l). The scale of radiance is expressed in 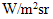
 , simulated for
, simulated for  Angular aperture of input beam: (a) 5°, 6°, 8°, 10°, 12°, 18°, 20°; (b) 30°, 40°, 50°, 60°, 70°, 80°, 90°
Angular aperture of input beam: (a) 5°, 6°, 8°, 10°, 12°, 18°, 20°; (b) 30°, 40°, 50°, 60°, 70°, 80°, 90°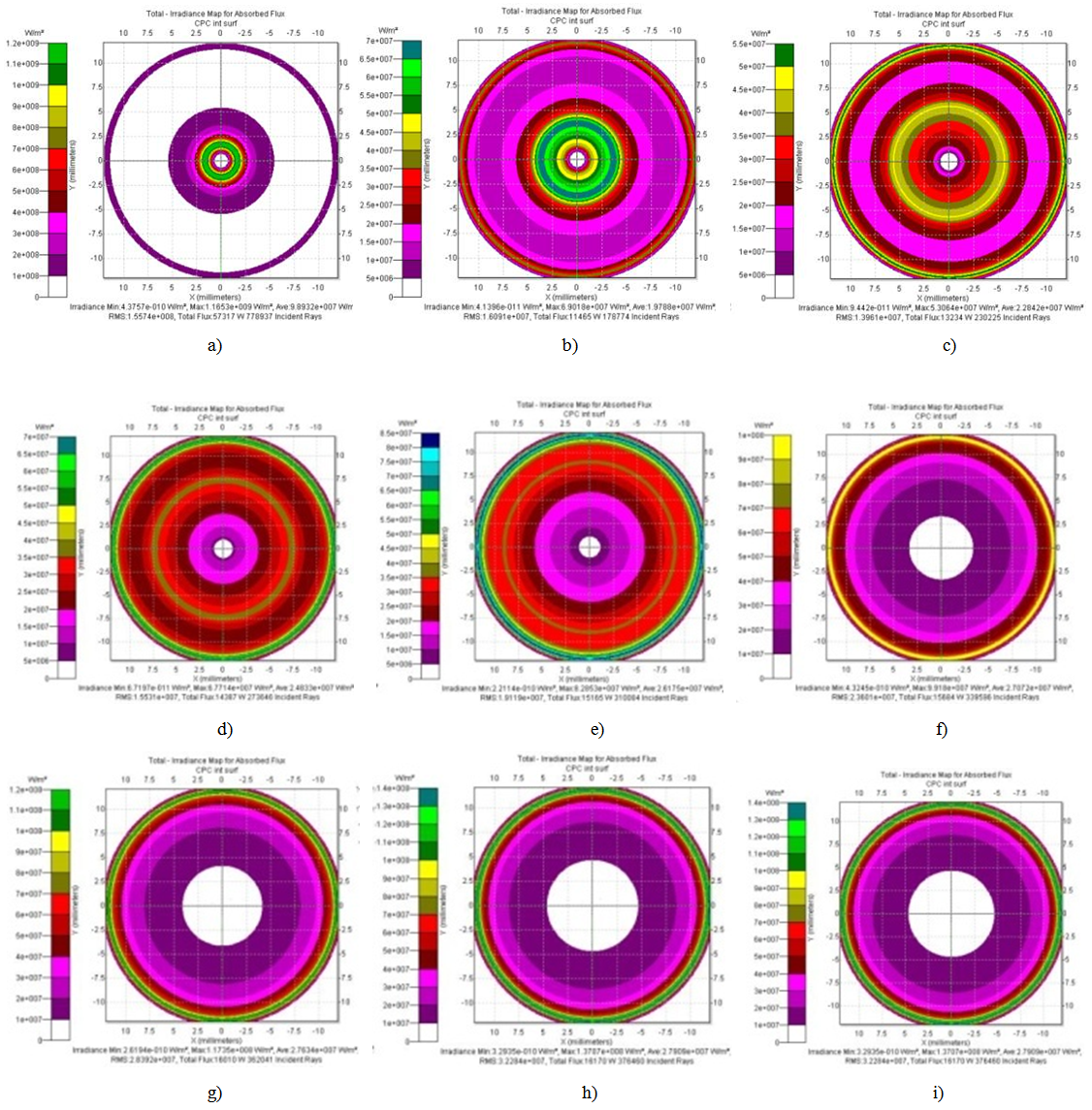
 = 10° (a); 20° (b); 30° (c); 40° (d); 50° (e); 60° (f); 70° (g); 80° (h) ; 90° (i). Wall reflectivity:
= 10° (a); 20° (b); 30° (c); 40° (d); 50° (e); 60° (f); 70° (g); 80° (h) ; 90° (i). Wall reflectivity:  = 0.9
= 0.9
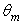 from 2° to 20° (a) and from 2° to 80° (b). Wall reflectivity:
from 2° to 20° (a) and from 2° to 80° (b). Wall reflectivity: