-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Optics and Applications
p-ISSN: 2168-5053 e-ISSN: 2168-5061
2015; 5(3): 58-64
doi:10.5923/j.optics.20150503.02
Analysis of Total Harmonic Distortion in an APD Receiver Circuit
Faramarz E. Seraji
Optical Communication Group, Iran Telecom Research Center, Tehran, Iran
Correspondence to: Faramarz E. Seraji, Optical Communication Group, Iran Telecom Research Center, Tehran, Iran.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
This paper presents a simple analysis on the nonlinear behavior of a practical APD receiver circuitry, by considering a silicon APD photodetector as an optical receiver. The analysis presents the effects of received input power by the photodetector and the load resistance at the receiving end on the total harmonic distortion (THD), consisting of second- and third harmonics. The behavior of the THD is formulated and graphically illustrated in terms of the input power and load resistance. Typically, for a given circuit, the second HD was found to be -71 dB, for load resistance of 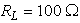 and optical input power of
and optical input power of 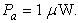 If a high impedance preamplifier is used with
If a high impedance preamplifier is used with 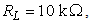 the second HD will worsen to a value of -11 dB for
the second HD will worsen to a value of -11 dB for 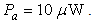 The analysis is given in an easy-to-understand manner that can be readily applied to a practical system and would be useful when dealing with analog optical fiber communication systems and optical fiber sensing systems.
The analysis is given in an easy-to-understand manner that can be readily applied to a practical system and would be useful when dealing with analog optical fiber communication systems and optical fiber sensing systems.
Keywords: Total harmonic distortions (THD), APD receiver, Load resistance
Cite this paper: Faramarz E. Seraji, Analysis of Total Harmonic Distortion in an APD Receiver Circuit, International Journal of Optics and Applications, Vol. 5 No. 3, 2015, pp. 58-64. doi: 10.5923/j.optics.20150503.02.
Article Outline
1. Introduction
- In fiber sensor circuits, particularly when operating at a wavelength of 633 nm or 830 nm, a silicon avalanche photo diode (APD) is often used as a detector in the receiver. At higher wavelengths Ge and InGaAs type of APD's with moderate gain are used for detection purposes [1-3].In analog optical communication links, in interferometric optical fiber sensors, and in analog radio-over-fiber systems, the performance at the receiving end is limited by second order nonlinearity, which is induced by the photodiode acting as the photodetector [4-13]. That is, the degree of nonlinearity of the photodiode is determined by the total harmonic distortion appearing at the output power which in particular includes the second and third order harmonic components [13]. Works have been reported to improve the linearity of photodiodes for the frequency range of 1-2 GHz. [14, 15]. In another attempt, a method was used to improve higher frequency performance of photodiodes by using Mach-Zehnder modulator (MZM) at quadrature bias with balanced detection to nullify the second order nonlinearity of photodiode at high frequencies [16].In a recent report, yet another method used dual parallel MZM to cancel out the photodiode-induced second harmonic distortion [17]. It was shown that the second harmonic generated by this method was 180 deg. out of phase of that of the photodiode nonlinearity. Recently, the nonlinearity of a commercial photodiode was measured, using three setups of a one-tone heterodyne, two-tone heterodyne and three-tone MZM designs. Mathematically developed data on multiple devices are compared to find under which conditions the measurements by three setups are comparable [18]. A new method is reported theoretically with experimental results to cancel even-order distortion induced by photodiode in microwave photonic links. A single Mach-Zehnder modulator, biased slightly away from the quadrature point, is shown to suppress photodiode second-order intermodulation distortion in excess of 40 dB without affecting the fundamental power [19].In an another report, a measurement of the nonlinearity responsivity of two commercial photodiodes of types p-n Ge and p-i-n InGaAs, used in optical fiber power measurements, was presented. The photodiodes in measurements were under high irradiance levels. It was shown that the photodiodes nonlinearities were of the saturation type, which depended on the beam diameter of the radiation source [20]. In newly reported work, a model of simulating photodiode microwave nonlinearities is proposed, which includes the effects of non-uniform absorption in three dimensions and self-heating of the photodiode. The saturated output power and third order output intercept points of two different waveguide photodiodes are simulated, with excellent agreement between measurement and theory [21].In an early work, a simple method was used to obtain harmonic distortion levels of a pin photodiode at different frequencies from the microwave reflection coefficient of the photodiode under dc illumination for different incident optical powers [22].The gain of the APD is a function of the actual bias voltage across the diode, and if the output voltage across the load resistance changes corresponding to a change in the received optical power, the bias voltage of the APD gets modulated leading to a non-linear response of the overall APD receiver. However, when receiving weak optical signals, this non-linearity will be acceptably small [23].In this paper, a simple analysis on the nonlinear behavior of a practical silicon APD photodetector circuitry is presented, by considering the gain characteristics of the APD photodiode. The analysis of the total harmonic distortion (THD), which is an indication of degree of nonlinearity in an APD photodetector, includes the effects of received input power and the load resistance at the receiving output. The behavior of the THD is formulated and graphically illustrated in terms of the input power and load resistance.The analysis is given in an easy-to-understand manner that can be readily applied to a practical system and would be useful when dealing with the optical fiber sensor systems and analog optical fiber communication systems.
2. Distortion in APD Receiver
- Figure 1 shows a practical circuit diagram of an APD receiver using a silicon APD. The resistor
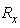 is being used to protect the avalanche photodiode from an accidental break-down, if any, by limiting the maximum possible current flow. The capacitors at the cathode of the APD keeps the voltage at the cathode
is being used to protect the avalanche photodiode from an accidental break-down, if any, by limiting the maximum possible current flow. The capacitors at the cathode of the APD keeps the voltage at the cathode 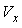 at ac ground. Figure 2 shows the plot of the APD gain
at ac ground. Figure 2 shows the plot of the APD gain 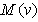 as a function of the bias voltage, obtained experimentally. Around the break-down voltage of the APD, the gain of the receiver increases rapidly.
as a function of the bias voltage, obtained experimentally. Around the break-down voltage of the APD, the gain of the receiver increases rapidly.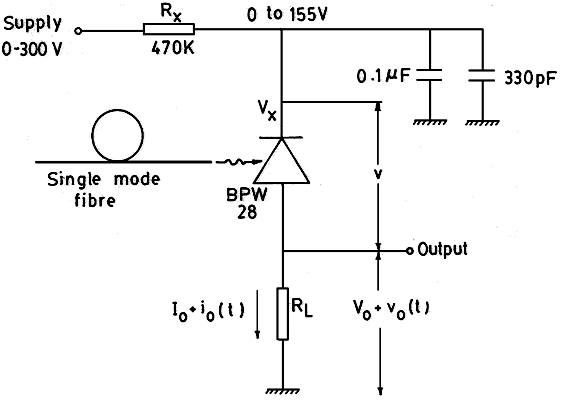 | Figure 1. Circuit diagram of the APD receiver |
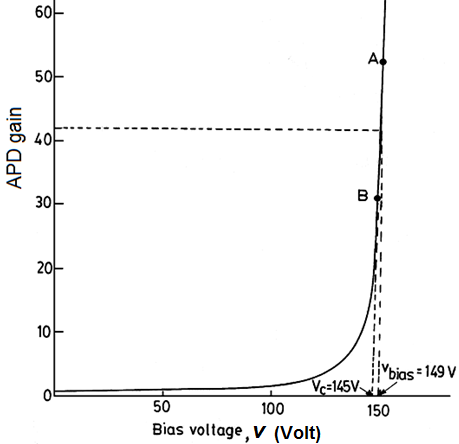 | Figure 2. Characteristic curve of the APD gain at 5 kHz as a function of APD bias voltage for a peak ac optical input power 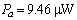 |
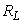 and the ac output voltage
and the ac output voltage 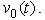 For a given dc bias voltage
For a given dc bias voltage 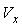 at the cathode of the APD (in Fig. 1), the actual voltage
at the cathode of the APD (in Fig. 1), the actual voltage 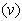 across APD changes with the output voltage as
across APD changes with the output voltage as  where
where  is the dc voltage across
is the dc voltage across  At a given average optical power level,
At a given average optical power level, 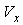 and
and 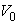 will remain constant but
will remain constant but 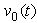 will change with the modulation in the optical power. Since
will change with the modulation in the optical power. Since 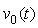 itself is a function of the actual APD bias voltage, distortion results when the output voltage modulates the APD gain. This effect will be worse whenever the load resistance and the optical signal level (and hence the electrical output signal voltage) are high.The APD gain characteristic curve of Fig. 2 can be assumed to be linear over a small range of the APD bias voltage and accordingly can be expressed by a straight line equation. This assumption is valid when receiving a small optical signal and helps in simplifying the distortion analysis. For example, the curve AB of Fig. 2 can be expressed as:
itself is a function of the actual APD bias voltage, distortion results when the output voltage modulates the APD gain. This effect will be worse whenever the load resistance and the optical signal level (and hence the electrical output signal voltage) are high.The APD gain characteristic curve of Fig. 2 can be assumed to be linear over a small range of the APD bias voltage and accordingly can be expressed by a straight line equation. This assumption is valid when receiving a small optical signal and helps in simplifying the distortion analysis. For example, the curve AB of Fig. 2 can be expressed as: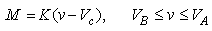 | (1) |
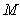 is the gain of the APD,
is the gain of the APD, 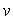 is the instantaneous bias voltage across the APD,
is the instantaneous bias voltage across the APD, 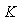 is a constant equal to the slope of curve AB, and
is a constant equal to the slope of curve AB, and 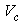 is the voltage as indicated in Fig. 2, obtained by extending the line passing through points A and B. Equation (1) is valid only for points along the curve AB. The value of
is the voltage as indicated in Fig. 2, obtained by extending the line passing through points A and B. Equation (1) is valid only for points along the curve AB. The value of 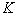 for Fig. 2 was calculated to be about 11.197
for Fig. 2 was calculated to be about 11.197 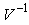 and
and 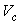 was equal to 145
was equal to 145 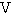 .An expression for the current multiplication factor
.An expression for the current multiplication factor 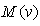 has been given as [24]:
has been given as [24]: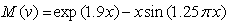 | (2) |
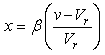 | (3) |
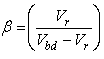 | (4) |
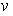 is the instantaneous reverse bias voltage,
is the instantaneous reverse bias voltage, 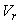 is the reverse voltage at which avalanche multiplication becomes significant, and
is the reverse voltage at which avalanche multiplication becomes significant, and 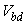 is the reverse breakdown voltage of the APD. In this case the slope,
is the reverse breakdown voltage of the APD. In this case the slope, 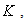 of the characteristic curve is given by:
of the characteristic curve is given by: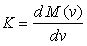 | (5) |
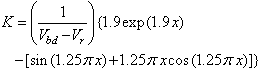 | (6) |
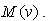 For a given bias voltage of
For a given bias voltage of 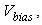 the value of
the value of 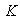 can be evaluated from Eq. (6) along a linear segment PQ shown on the curve in Fig. 3. The value of
can be evaluated from Eq. (6) along a linear segment PQ shown on the curve in Fig. 3. The value of 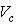 on the
on the 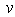 -axis can then be evaluated by:
-axis can then be evaluated by: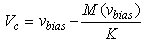 | (7) |
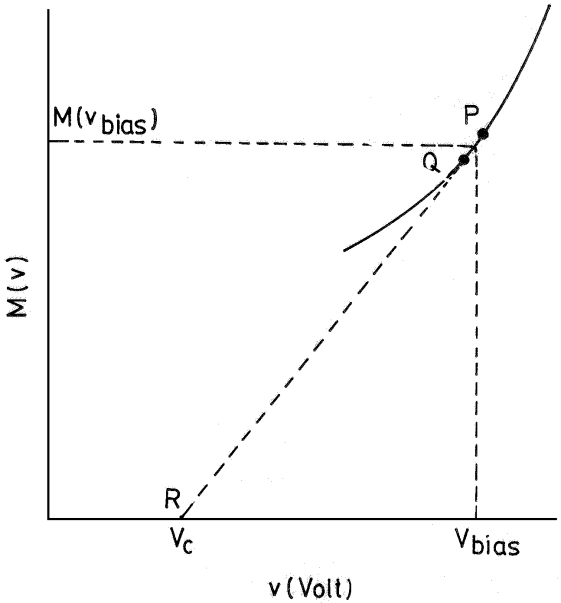 | Figure 3. A general characteristics curve of APD for evaluation of  and and  from the equation of from the equation of 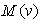 |
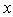 up to 0.8 [24]. More accurate expression for
up to 0.8 [24]. More accurate expression for 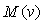 , if any, can be used instead of Eq. (2) without any loss of generality.
, if any, can be used instead of Eq. (2) without any loss of generality.3. Derivation of Harmonic Distortion in APD
- To derive the expression for harmonic distortion in the APD circuit, we will consider the linearized characteristic curve (AB in Fig. 2) over a small range around the operating point of the APD voltage. The expression for the instantaneous ac current
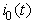 generated by the APD receiver corresponding to an ac input optical power
generated by the APD receiver corresponding to an ac input optical power 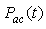 can be written, referring to Eq. (1), as:
can be written, referring to Eq. (1), as: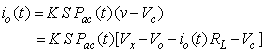 | (8) |
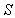 is the responsivity of the photodiode (with gain equal to unity). After rearranging Eq. (8) we obtain:
is the responsivity of the photodiode (with gain equal to unity). After rearranging Eq. (8) we obtain: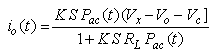 | (9) |
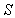 at an angular frequency
at an angular frequency 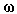 expressed as:
expressed as: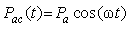 | (10) |
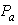 is the peak amplitude of the ac optical power. The optical power
is the peak amplitude of the ac optical power. The optical power 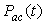 does not contain any dc component and is equal to the instantaneous optical power minus the dc component of the optical power
does not contain any dc component and is equal to the instantaneous optical power minus the dc component of the optical power  . Substituting for Pac(t) in Eq. (9), we get:
. Substituting for Pac(t) in Eq. (9), we get: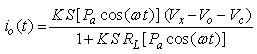 | (11) |
 can be alternatively shown as:
can be alternatively shown as: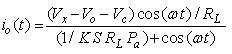 | (12) |
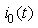 by the load resistance
by the load resistance 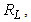 the instantaneous ac output voltage
the instantaneous ac output voltage 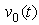 can be obtained as:
can be obtained as: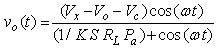 | (13) |
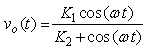 | (14) |
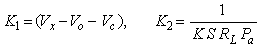 | (15) |
3.1. Fourier Series Expansion of the ac Output Voltage of the APD
- In general, the Fourier transform of the periodic signal
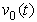 (Eq. 14) in interval
(Eq. 14) in interval 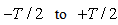 can be expressed as:
can be expressed as: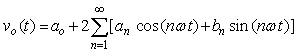 | (16) |
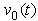 is an even function, the coefficient
is an even function, the coefficient 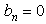 ; then Eq. (16) simplifies to:
; then Eq. (16) simplifies to: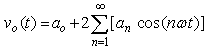 | (17) |
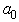 is the average value of
is the average value of 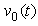 given by:
given by: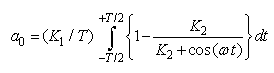 | (18) |
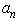 is given as:
is given as: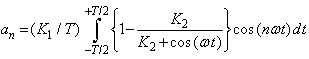 | (19) |
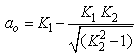 | (20) |
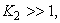 one obtains
one obtains 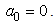 To determine the value of
To determine the value of 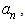 we proceed as follows. From Eq. (19), we can write:
we proceed as follows. From Eq. (19), we can write: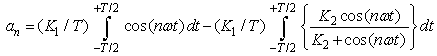 | (21) |
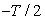 to
to 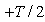 is zero, then we have:
is zero, then we have: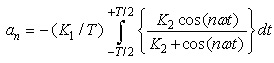 | (22) |
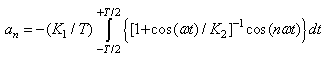 | (23) |
 we can expand the term in the bracket in Eq. (23) as:
we can expand the term in the bracket in Eq. (23) as: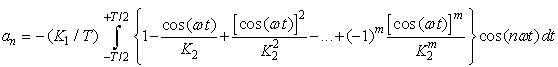 | (24) |
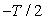 to
to 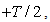 the first term in Eq. (24) is zero. Therefore,
the first term in Eq. (24) is zero. Therefore, 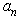 can be reduced to:
can be reduced to: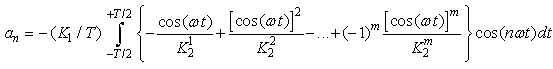 | (25) |
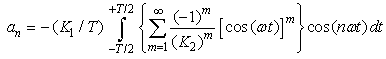 | (26) |
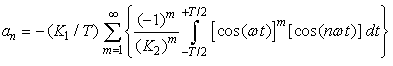 | (27) |
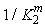 tends to zero for high values of
tends to zero for high values of 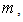 by assuming
by assuming 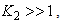 the expression for
the expression for 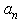 can be approximated by limiting the maximum value of
can be approximated by limiting the maximum value of 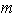 to 5. The total harmonic distortion (THD), which indicates the degree of nonlinearity of an APD receiver, can be characterized by an analysis of the output spectral components with an input driven by a pure sinewave. Therefore, the THD in dB and percentage (%) can be defined, respectively, as [25-27]:
to 5. The total harmonic distortion (THD), which indicates the degree of nonlinearity of an APD receiver, can be characterized by an analysis of the output spectral components with an input driven by a pure sinewave. Therefore, the THD in dB and percentage (%) can be defined, respectively, as [25-27]: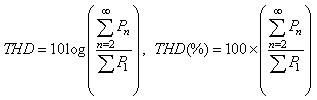 | (28) |
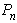 and
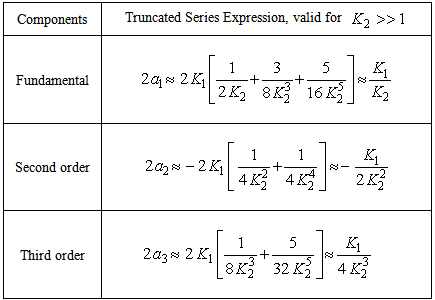
and 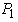 are total signal powers and fundamental signal power, respectively.Table 1 lists the approximate expressions for the different Fourier coefficients in terms of fundamental, second- and third harmonics components. From these expressions, second- (HD)2 and third harmonic distortion (HD)3 in dB, with respect to the fundamental, can be calculated, respectively, as:
are total signal powers and fundamental signal power, respectively.Table 1 lists the approximate expressions for the different Fourier coefficients in terms of fundamental, second- and third harmonics components. From these expressions, second- (HD)2 and third harmonic distortion (HD)3 in dB, with respect to the fundamental, can be calculated, respectively, as: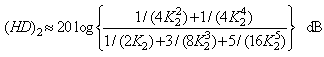 | (29) |
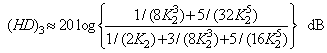 | (30) |
|
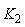 can be determined from Eq. (15) for a given values of
can be determined from Eq. (15) for a given values of 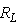 and
and 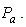 The harmonic distortion will be low, if the value of
The harmonic distortion will be low, if the value of 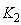 is high. In other words, the distortion value will be low, when either the APD receiver's load resistance
is high. In other words, the distortion value will be low, when either the APD receiver's load resistance 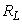 or the peak optical power
or the peak optical power 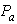 is small.
is small.4. Results of the Distortion Analysis
- The harmonic distortion values were computed for load resistance of
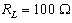 for different peak values of ac optical power
for different peak values of ac optical power 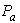 . The plot is shown in Fig. 4, at
. The plot is shown in Fig. 4, at 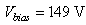 for which
for which 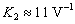 and
and 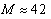 . The second HD was about -71 dB (below fundamental) at
. The second HD was about -71 dB (below fundamental) at 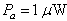 which increased to -31 dB at
which increased to -31 dB at 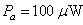 for
for 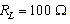 . The corresponding theoretical value of third HD was -142 dB and -62 dB, respectively. The corresponding THD values are -214 dB for
. The corresponding theoretical value of third HD was -142 dB and -62 dB, respectively. The corresponding THD values are -214 dB for 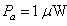 and -93 dB for
and -93 dB for 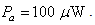
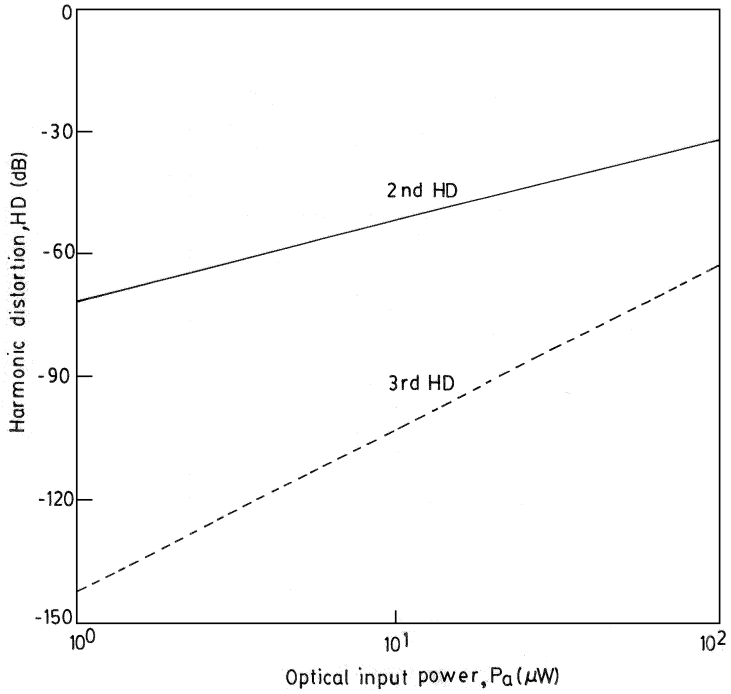 | Figure 4. Theoretical harmonic distortion of the APD receiver versus peak optical input power 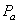 for load resistance for load resistance 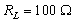 |
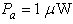 and
and 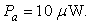 At
At 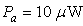 , the second HD increases from a value of about -51 dB for
, the second HD increases from a value of about -51 dB for 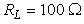 to a value of about -11 dB for
to a value of about -11 dB for 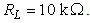
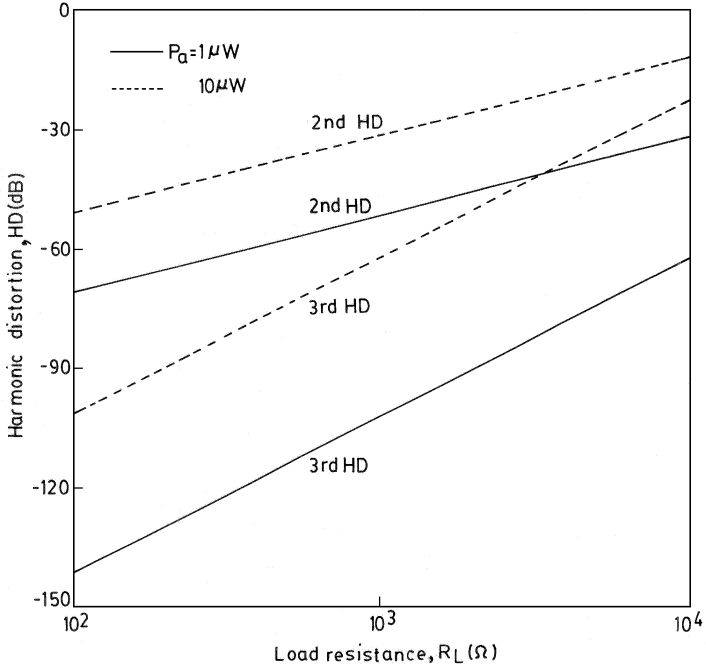 | Figure 5. Theoretical harmonic distortion of the APD receiver versus load resistance  for peak optical input power for peak optical input power  and and  |
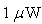 and
and 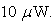 The results indicate that when the load resistance is lower, the THD is also lower for a specified received optical power.
The results indicate that when the load resistance is lower, the THD is also lower for a specified received optical power.
|
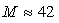 and
and 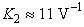 . For low load resistance, when received power has increased 10 times, the THD only increased to 9 dB, i.e. 4.7% degradation, whereas for high load resistance, the same power increase would cause an increase of 53 dB in the THD, which corresponds to 61% degradation of the THD. That is to say for a high load resistance, a 10 order of magnitude increase in received power, would result in 13 order of magnitude degradation in the THD. For a general APD characteristic
. For low load resistance, when received power has increased 10 times, the THD only increased to 9 dB, i.e. 4.7% degradation, whereas for high load resistance, the same power increase would cause an increase of 53 dB in the THD, which corresponds to 61% degradation of the THD. That is to say for a high load resistance, a 10 order of magnitude increase in received power, would result in 13 order of magnitude degradation in the THD. For a general APD characteristic 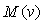 given by Eq. (2), the value of
given by Eq. (2), the value of 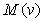 and
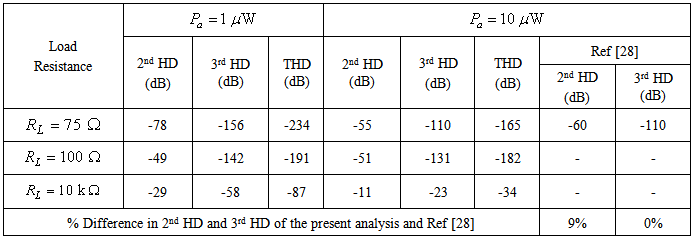
and 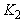 at different APD bias voltages can be theoretically evaluated, and from Table 1, the harmonic distortion values can be accordingly calculated.For sake of comparison, to the best of our knowledge a newer than the Ref. [28] was not traced to have reported an experimental replica of the present analysis. The then experimental results showed that for an optical input power of 10
at different APD bias voltages can be theoretically evaluated, and from Table 1, the harmonic distortion values can be accordingly calculated.For sake of comparison, to the best of our knowledge a newer than the Ref. [28] was not traced to have reported an experimental replica of the present analysis. The then experimental results showed that for an optical input power of 10 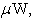 the second order (HD) and third order harmonic distortions were found to be -60 dB and -118 dB, respectively. The biasing voltage was 155 V, the gain was 76, and the load resistance was 75
the second order (HD) and third order harmonic distortions were found to be -60 dB and -118 dB, respectively. The biasing voltage was 155 V, the gain was 76, and the load resistance was 75 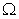 In the present analysis, for a gain of 42, biasing voltage of 145 V, and input power of 10
In the present analysis, for a gain of 42, biasing voltage of 145 V, and input power of 10 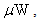 the second order HD and third order HD are found to be -55 dB and -110 dB, respectively, for the same load resistance at 75
the second order HD and third order HD are found to be -55 dB and -110 dB, respectively, for the same load resistance at 75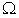 In Table 2, it shown that the percentage differences between 2nd HDs of the present analysis and Ref [28] is 9% and for 3rd HDs is nil.
In Table 2, it shown that the percentage differences between 2nd HDs of the present analysis and Ref [28] is 9% and for 3rd HDs is nil.5. Conclusions
- In this paper, a simple model is proposed to compute the total harmonic distortion in an APD receiver circuit. The model is explained, by using the gain characteristic curve of an experimental circuit. For making the approach more general, a procedure is given so that the whole analysis could be based on an analytical equation of the gain
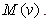 Direct expressions, for the second and third harmonic distortions in dB (with reference to the fundamental), are derived.It is shown that when input power increases, the 2nd HD and 3rd HD would increase, and at a given input power, the 2nd HD is higher than 3rd HD. Typically, for the given circuit, the THD was found to be -191 dB, for
Direct expressions, for the second and third harmonic distortions in dB (with reference to the fundamental), are derived.It is shown that when input power increases, the 2nd HD and 3rd HD would increase, and at a given input power, the 2nd HD is higher than 3rd HD. Typically, for the given circuit, the THD was found to be -191 dB, for 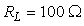 and
and 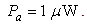 If a high impedance preamplifier is used with
If a high impedance preamplifier is used with 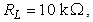 the THD will become worse to a value of -34 dB for
the THD will become worse to a value of -34 dB for 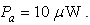 The results of the analysis indicates that for low THD, the load resistance and the received optical power at the output end should be at low level. In a given comparison shows that the obtained results almost tally with a reported experimental results.The analysis presented here will be useful for analog optical fiber transmission systems and optical sensor applications.
The results of the analysis indicates that for low THD, the load resistance and the received optical power at the output end should be at low level. In a given comparison shows that the obtained results almost tally with a reported experimental results.The analysis presented here will be useful for analog optical fiber transmission systems and optical sensor applications. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML