Adnan Salih Al-ithawi
Baghdad University, Collge of Sciencs for Women
Correspondence to: Adnan Salih Al-ithawi, Baghdad University, Collge of Sciencs for Women.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Neither the pure wave theory nor the pure particle theory can explain the nature of light. Light must be both a particle and a wave. It is a wave because it exhibits interference effects. At the same time, the fact that the photographs contain discrete dots is a direct demonstration that light refuses to be split into units of less than a single photon. We found a general equations that solved all the problems in the current theories for the photon and explained the nature of light by suggesting new hypotheses. According to our results, the photon is a particle which has mass and associated with a wave. The results of the research proved that the refractive index of materials varies with the natural mass of the photon.
Keywords:
Photon, Mass, Energy, Particle, Wave
Cite this paper: Adnan Salih Al-ithawi, The Photon as a Mass Particle Associated with a Wave, International Journal of Optics and Applications, Vol. 5 No. 1, 2015, pp. 22-25. doi: 10.5923/j.optics.20150501.03.
1. Introduction
Until recently, light has been the biggest secret in physics, its dual nature has not been resolved nor its exact constitutes were known. Huygens showed that reflection, refraction, partial reflection and refraction, diffraction, interference, etc are typical properties of Electromagnetic (EM) Waves. Therefore, everyone agreed that light is a wave.Later, the Compton and the famous photoelectric effects were discovered. However, the problem was that the electrons that were liberated from metal surfaces one after another in the photoelectric effect showed that a particle of equal or more energy collided with the electron to liberate it from the metal surface. As a result, Einstein had no choice but to introduce the concept of an imaginary photon which has zero mass and other ideal properties. The exact nature of light is, somehow, between the state of being a wave and also a particle of zero mass. Light seems to behave like a wave in some cases and like a particle in other cases. The Photons is a concept that developed just for the sake of an important discovery like photoelectric effect.Neither the pure wave theory nor the pure particle theory can explain the results. If light was only a particle and not a wave, there would be no interference effect. The result of the experiment would be like firing a hail of bullets through a double slit. Only two spots directly behind the slits would be hit. If, on the other hand, light was only a wave and not a particle, we would get the same kind of diffraction pattern that would happen with a water wave. There would be no discrete dots in the photo, only a diffraction pattern that shaded smoothly between light and dark.Applying the definitions to this experiment, light must be both a particle and a wave. It is a wave because it exhibits interference effects. At the same time, the fact that the photographs contain discrete dots is a direct demonstration that light refuses to be split into units of less than a single photon.Equations that are using to calculate the properties of photon according to wave or particle theories has some problems in applications, The famous E = mc2 energy/mass equivalence relation breaks down in the case of photons in dispersive media [1].The photon is a mass less particle. According to theory it has energy and momentum but no mass and this is confirmed by experiment to within strict limits In modern terminology the mass of an object is its invariant mass which is zero for a photon [2].The momentum of photon in dispersive medium is of conceptual and practical importance [3-8].The problem of determining which momentum is ‘correct’ is the famous Abraham–Minkowski dilemma. This is not the place to review the large literature devoted to this problem; instead, we recommend to the interested reader the review by [9] and the more recent one of [10]. As theory has presented us with a dilemma, it is reasonable to seek an answer in experiments, and this idea has been pursued on a number of occasions [11-14].All the problems that appears with the applications of the current equations when calculate the parameters of photon, because of principles of derivatives, so we need a new hypotheses to solve these problems.
2. Current Equations
In brief, we can demonstrate the equations that are used to calculate the energy, mass, momentum and wavelength of photon as follows: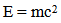 | (1) |
Surprisingly, Einstein never derived nor ever accepted this relation. Equation (1) was becoming the most widely recognized symbol of atomic Age, Einstein maintained that this general statement was formulated "somewhat inexactly" [15].It also turns out that, we are able to define the concept of "energy" E, such that E has simple and well-defined properties just like those it has in Newtonian mechanics. When a particle has been accelerated so that it has some momentum p (the length of the vector p) and relativistic mass mrel, then its energy E turns out to be given by: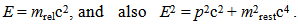 | (2) |
There are two interesting cases of the equation (2):• If the particle is at rest, then p = 0, and E = mrestc2.• If we set the rest mass equal to zero (regardless of whether or not that's a reasonable thing to do), then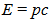 | (3) |
In modern terminology the mass of an object is its invariant mass which is zero for a photon. In special relativity, the mass of photon,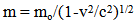 | (4) |
When the term relativistic mass(Eq.4) became popular, Einstein silently eschew edit [16].When the object in rest state mo=m and the velocity increase, the effective mass increase also, but when the velocity v=c, then the effective mass is not define. So equation (2) cannot used for photon.The momentum of photon in vacuum according to current theory is: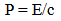 | (5) |
According to mikowisky's and Abraham's equations for momentum of photon in medium: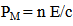 | (6) |
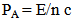 | (7) |
From equations (6), (7), and (3),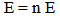 | (8) |
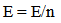 | (9) |
Which is correct (8) or (9), while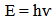 | (10) |
From (10) (E) is constant as in current theory.The wavelength of photon is decrease in medium according to refractive index: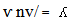 | (11) |
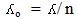 | (12) |
Where 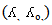 is the wavelength in vacuum, and medium respectively. and(ѵ ) is the frequency of photon,( n) is the refractive index. When the velocity (v) of light in medium (v=0),then=
is the wavelength in vacuum, and medium respectively. and(ѵ ) is the frequency of photon,( n) is the refractive index. When the velocity (v) of light in medium (v=0),then= 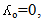 and (ѵ=0/0).All the problems that appears with the applications of the current equations when calculate the parameters of photon, because of,• The assumptions that the object at rest and accelerated to some velocity.• The photon is wave and exhibits, in some cases, the behavior of a particle without mass.As we know that, the photon is always moving at speed of light in space, so the equations above are not suitable for photon. We thought that, a new hypotheses must be using to solve these problems.
and (ѵ=0/0).All the problems that appears with the applications of the current equations when calculate the parameters of photon, because of,• The assumptions that the object at rest and accelerated to some velocity.• The photon is wave and exhibits, in some cases, the behavior of a particle without mass.As we know that, the photon is always moving at speed of light in space, so the equations above are not suitable for photon. We thought that, a new hypotheses must be using to solve these problems.
3. New Hypotheses
The nature of the photon is the measurements that we make of it. The concept of the photon is basically just what we might think the photon “looks like”. While there is only one set of measurements of the photon’s nature, everyone has a different concept of just what the photon might really be.All measurements show that the photon has mass. The metaphysical assumption of a mass less photon is completely without any experimental verification. Experimental physics has measured the photon in nearly every way possible and technology has exploited the nature of the photon to a remarkable extent. Collectively these measurements all measure the nature of the photon’s mass. Each idea of a mass less photon is someone’s concept of the photon that makes it possible to ignore certain aspects of photon measurementsTo solve the problems that appears with the current theories, we suggesting that;1-A new definition for rest mass2-The energy of photon in medium divided to kinetic and potential energies. Photon as particle has massAccording to statement (1), the new definition of rest mass (mo) is: the mass when the object in natural state without any external effect (mnat). According to this definition, the natural mass can be calculated from equation: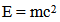 | (1) |
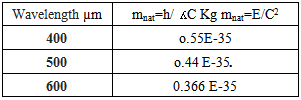
From equation (1), the different photons has different non-zero natural mass as shown in table (1)Table (1).
 |
| |
|
Table (1) represent the relation between wavelength and natural mass.According to this definition, when the particle (photon( is at speed of light (c), its mass has a minimum value called the "natural mass" mnat. The natural mass is always the same for the same type of photon. As the photon is decelerated to ever lower speeds in medium, its relativistic mass "mrel" increases without limit [17]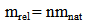 | (13) |
Where (n) is the refractive index, in vacuum (n =1), then mrel = mnat, while when the velocity of photon decrease in medium the refractive index increase and the relativistic mass increase also.To calculate the energy of photon, in medium and vacuum, According to hypotheses (2), [17]: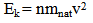 | (14) |
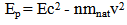 | (15) |
Where (Ek kinetic energy, Ep is the potential energy), (E) total energy, (v)is the velocity of photon in medium, (n) refractive index.Now in vacuum (n=1), and (v=c), so Ep =0and equation (14) became equation (1).This mean that equation (14) is a general equation, while equation (1) is special case.From this theory the momentum is constant in and outside in medium [17]: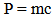 | (16) |
Photon as particle has WaveThe current theories assumed that the energy must be constant in and outside of medium as in equation (10). To solve the controversy of (8), and (9), we assume that the energy of photon in medium divided to kinetic energy and potential energy, according to reference [17]: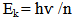 | (17) |
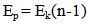 | (18) |
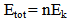 | (19) |
From equations (6), (7), and (17), The momentum in vacuum and medium is the same as in equation (16). When n=1, Ep=0 and equation (17) became (10).This mean that equation (17) is a general equation, while equation (10) is special case.In the current theory, the wavelength of photon is decrease in medium according to refractive index as in equation (12), to solve this problem;The new theory supposed that the wave length remain constant in and outside of medium because• when the wave inter to medium all parts will distributed by the same magnitude in opposite direction of the operator, this mean that the length of wave does not change.• the light wave is transverse wave, so the top of wave will inter firstly, so the amplitude will change which leads to decrease the kinetic energy of photon as in equation (17).When the photon inter medium, the velocity will decrease according to nature of medium, then the velocity (c) will be (n v). According to this statement, the frequency and the wavelength of photon must be constant.The concept of wave-particle duality has been generalized by de Broglie [18] to apply to all types of matter.In new theory, the relation between wavelength and mass of photon can be derived from equations (1), (13)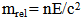 | (20) |
From equation (10), (20) 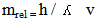 | (21) |
This equation is similar to DeBroglie equationComparative between this theory and current theoriesWe can compare between the equations of this theory and current theories as in the flowing table (2).Table (2).
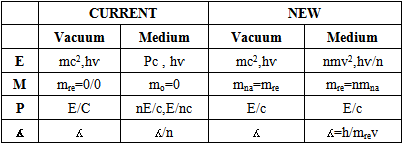 |
| |
|
Table (2) comparative between the equations of different theoriesNow let a photon with energy (2*10-19 J) enter a medium with refractive index (1016).What is the energy, mass, and the momentum?The velocity of the photon is (v=c/n)=3*10-8 m/sThe results of this example are demonstrated in table (3).Table (3).
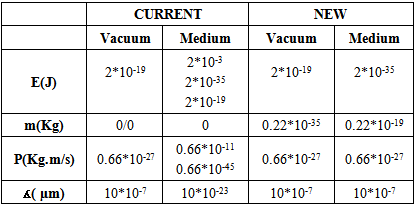 |
| |
|
A simple analysis for table (5), we can see that, both theories has the same results in vacuum(E, P, and ʎ), except the value of the mass of photon, and this because the new definition of rest mass. In medium , for current theories, the energy of photon has three magnitudes, if the photon is wave the energy is constant (2*10-19J), while if the photon is particle there are two results for (E,P) according to the Minkowisky and Abraham relations, the wave length decreased by factor (n). For this theory the magnitudes of (p, ʎ) are constant, while the energy is decreased (2*10-35J) which is approximately equal to value of natural mass (0.22*10-35Kg). The relative mass increased (0.22*10-19Kg) which is approximately equal to value of energy in vacuum (2*10-19J).
4. Dispersion
The refractive index of materials varies with the wavelength of light. This is called dispersion. In regions of the spectrum where the material does not absorb, the refractive index tends to decrease with increasing wavelength. According to Snell's law.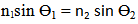 | (22) |
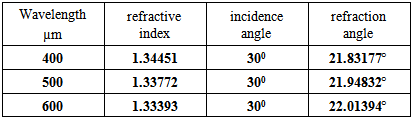
Where (n1, n2 are the refractive indices in vacuum and medium respectively, and (Ө1, Ө2, are the indicant and refractive angles respectively).The following table (4) shows numerical values for the refractive index of water as a function of wavelength in the visible part of the spectrum, and the refraction angle with incidence angle (30°).Table (4).
 |
| |
|
Table (4) shows numerical values for the refractive index of water as a function of wavelength in the visible part of the spectrum, and the refraction angle with incidence angle (30°).The question that will be explored in the present study is whether there is really no way of understanding light dispersion in terms of a particle model.From equation (13) and (22), we can find: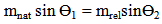 | (23) |
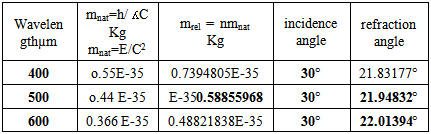
This new relation between refractive angle and the natural mass of photon. According to (23), the refractive index of materials varies with the natural mass of light.The following table (5) shows numerical values for the refraction angle of photon as a function of the natural mass in the visible part of the spectrum (the refractive index in water as in table (2), and with incidence angle (30°).Table (5).
 |
| |
|
As shown, in the two tables (4,5), the refraction angles are same according to equations (22, 23), These results proved that, the photon as a mass particle associated with a wave.
5. Conclusions
In this study, all problems associated with current theories solved, and we found general equations (14, 17), can be used to calculate mass, and energy of photon in vacuum, and medium.The results we found proved that, the photon is particle has mass and wave. The dispersion of light explained as the photon is particle and depends on the natural mass of photon. The mass and kinetic energy of photon are changeable while the momentum is constant.
References
| [1] | Albert Einstein,"E=Mc2", Ideas and Opinion 9Dell,New york,1976 p.330. |
| [2] | Stephen M. Barnett , Rodney Loudon, The enigma of optical momentum in a medium, DOI: 10.1098/rsta.2009.0207 Published 1 February 2010. |
| [3] | H. Minkowski, Naehr.Ges.Wiss ,Gottingen %3, 1908. |
| [4] | H. Minkowski, Math, Ann.68,472,1910. |
| [5] | M. Abraham, Rand.Circ.Mat.Palermo,28,1,1909. |
| [6] | M. Abraham, Rand.Circ.Mat.Palermo,30,33,1910. |
| [7] | J.P. Gorden, Phy.Rev.A 8,14,1773. |
| [8] | M.P.Haugan and F.V.Kowsiki, Phy.Rev.A 25 1982. |
| [9] | Brevik I. (1979) Experiments in phenomenological electrodynamics and the electromagnetic energy–momentum tensor. Phys. Rep. 52:133–201,(doi:10.1016/0370-1573(79)90074-7). |
| [10] | Pfeifer R. N. C., Nieminen T. A., Heckenberg N. R., Rubinsztein-Dunlop H. (2007) Colloquium: Momentum of an electromagnetic wave in dielectric media. Rev. Mod. Phys. 79:1197–1216, (doi:10.1103/RevModPhys.79.1197). |
| [11] | Jones R. V., Richards J. C. S. 1954 The pressure of radiation in a reflecting medium Proc. R. Soc. Lond. A 221 480–498 (doi:10.1098/rspa.1954.0043. |
| [12] | Ashkin A., Dziedzic J. M. (1973) Radiation pressure on a free liquid surface. Phys. Rev. Lett. 30:139–142, (doi:10.1103/PhysRevLett.30.139). |
| [13] | Walker G. B., Lahoz D. G., Walker G. (1975) Measurement of the Abraham force in a barium titanate specimen. can. J.Phys.53:2577-2586. |
| [14] | Jones R. V., Leslie B. 1978 The measurement of optical radiation pressure in dispersive media Proc. R. Soc. Lond. A 360 347–363 (doi:10.1098/rspa.1978.0072). |
| [15] | Einstein A 1905 Ann. Physik 17 891. |
| [16] | Eugene hecht ,Einstein on mass and enery Am.J.Phy.vol 77, no.9 2009. |
| [17] | Adnan Salih,mass,energy,and momentum of photon in medium, International Journalof Physical Sciences,vol,8 no.21,1192,2013. |
| [18] | de Broglie L 1926 Phil. Mag. 47 446; 1925 Ann. phys. 3 22. |

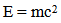
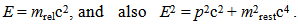
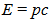
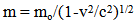
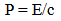
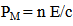
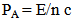
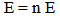
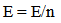
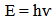
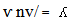
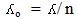
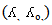 is the wavelength in vacuum, and medium respectively. and(ѵ ) is the frequency of photon,( n) is the refractive index. When the velocity (v) of light in medium (v=0),then=
is the wavelength in vacuum, and medium respectively. and(ѵ ) is the frequency of photon,( n) is the refractive index. When the velocity (v) of light in medium (v=0),then= 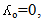 and (ѵ=0/0).All the problems that appears with the applications of the current equations when calculate the parameters of photon, because of,• The assumptions that the object at rest and accelerated to some velocity.• The photon is wave and exhibits, in some cases, the behavior of a particle without mass.As we know that, the photon is always moving at speed of light in space, so the equations above are not suitable for photon. We thought that, a new hypotheses must be using to solve these problems.
and (ѵ=0/0).All the problems that appears with the applications of the current equations when calculate the parameters of photon, because of,• The assumptions that the object at rest and accelerated to some velocity.• The photon is wave and exhibits, in some cases, the behavior of a particle without mass.As we know that, the photon is always moving at speed of light in space, so the equations above are not suitable for photon. We thought that, a new hypotheses must be using to solve these problems.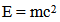
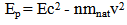
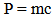
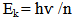
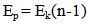
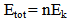
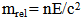
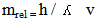
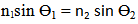
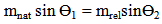
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML



