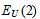-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Optics and Applications
p-ISSN: 2168-5053 e-ISSN: 2168-5061
2014; 4(3): 76-83
doi:10.5923/j.optics.20140403.02
Urbach Rule in Solid State Physics
Ihor Studenyak1, Mladen Kranjec2, Mykhailo Kurik3
1Physics Department, Uzhhorod National University, Uzhhorod, 88000, Ukraine
2Geotechnical Department, University of Zagreb, Varazdin, 42000, Croatia
3Institute of Physics, Ukrainian National Academy of Sciences, Prospect Nauki 46, 03680 Kyiv, Ukraine
Correspondence to: Ihor Studenyak, Physics Department, Uzhhorod National University, Uzhhorod, 88000, Ukraine.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
The paper is dedicated to the 60th anniversary of the Urbach rule. The Urbach edge behaviour, measured by optical absorption spectroscopy, is analysed for different solids. The general regularities of the Urbach rule revealed in crystalline and amorphous solids as well as the temperature behaviour of its main parameters are discussed. The main attention is paid to the studies of the possibilities of the Urbach rule parameters to be used for studying disordering processes in solids, short- and medium-range order in amorphous materials, specific features of the Urbach “bundle” in nanosystems and its variation in the vicinity of phase transitions. It is shown that the parameters obtained from the Urbach rule give an important information about dynamic properties of elementary excitations in condensed matter as well as about the interaction of electronic excitations with phonons.
Keywords: Absorption edge, Urbach rule, Exciton (electron)-phonon interaction, Disordering
Cite this paper: Ihor Studenyak, Mladen Kranjec, Mykhailo Kurik, Urbach Rule in Solid State Physics, International Journal of Optics and Applications, Vol. 4 No. 3, 2014, pp. 76-83. doi: 10.5923/j.optics.20140403.02.
Article Outline
1. Introduction
- In 1953 Franz Urbach, studying light absorption in AgBr crystals, was the first to observe experimentally an exponential increase of absorption coefficient with the photon energy while with increasing temperature the exponential parts of the absorption edge spectra formed a characteristic “bundle” [1]. Further research showed that the empirical regularity developed by Urbach for indirect-gap semiconductors [1], was later observed for direct-gap semiconductors [2] and a variety of crystalline and amorphous materials (e. g. [3–6]). The Urbach rule is revealed in layered (e.g. [7, 8]), chained (e.g. [9]) and nanodimensional (e.g. [10–12]) structures, ferroics (e.g. [9, 13–15]), and superionic conductors (e.g. [16–18]). Detailed reviews on the Urbach rule and main features of its manifestation in different materials were performed in Refs. [3, 6, 18–20]. Now the number of papers devoted to the Urbach rule is stabilized (approximately 10–15 papers annually).Sixty years have passed from the day of the development of the universal correlation between the absorption coefficient, the energy of incident photons and temperature practically for any types of optical transitions in condensed matter. Here we do not intend to summarize the research on the Urbach rule since it is impossible in the framework of an article. The aim of this paper is to trace the main directions and trends of modern application of the Urbach rule as well as to analyse the key problems to be solved in the future.
2. Main Features of Manifestation of the Urbach Rule in Crystalline Solids
- In the case of the Urbach behaviour of the absorption edge, the temperature and spectral dependence of absorption coefficient is described as [1]
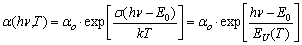 | (1) |
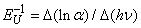 , σ is the steepness parameter of the absorption edge,
, σ is the steepness parameter of the absorption edge, 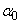 and
and 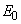 are the coordinates of the convergence point of the Urbach “bundle”. The exponential increase of the absorption coefficient in the range of the absorption edge is explained by transitions between the tails of density-of-states in the valence band and the conduction band, the shape and size of these tails depend on the presence of different types of disordering [4]. Figure 1 presents typical spectral dependences of absorption coefficient for different temperatures, illustrating the Urbach absorption edge in Cu7GeSe5I crystal [21]. It should be noted that Cu7GeSe5I crystal is one of the most efficient superionic conductors among copper-containing solid electrolytes [21]. A characteristic “bundle” of straight lines which meet in a point with coordinates
are the coordinates of the convergence point of the Urbach “bundle”. The exponential increase of the absorption coefficient in the range of the absorption edge is explained by transitions between the tails of density-of-states in the valence band and the conduction band, the shape and size of these tails depend on the presence of different types of disordering [4]. Figure 1 presents typical spectral dependences of absorption coefficient for different temperatures, illustrating the Urbach absorption edge in Cu7GeSe5I crystal [21]. It should be noted that Cu7GeSe5I crystal is one of the most efficient superionic conductors among copper-containing solid electrolytes [21]. A characteristic “bundle” of straight lines which meet in a point with coordinates 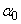 and
and 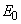 is clearly revealed. Such “bundle” (Fig. 1) should be observed within the absorption coefficient variation by few orders of magnitude and in a broad temperature range, as a rule, above the Debye temperature. It should be noted that the Urbach bundle is observed as a result of Wannier-Mott exciton smearing in semiconductor and ionic crystals, as a result of Frenkel exciton smearing in molecular crystals as well as a result of smearing of interband optical transitions in non-exciton solids [3]. In some cases deviations from the Urbach behaviour occur, i.e. the shape of the optical absorption edge is still exponential, but the extrapolated linear parts do not converge in a focus with the coordinates
is clearly revealed. Such “bundle” (Fig. 1) should be observed within the absorption coefficient variation by few orders of magnitude and in a broad temperature range, as a rule, above the Debye temperature. It should be noted that the Urbach bundle is observed as a result of Wannier-Mott exciton smearing in semiconductor and ionic crystals, as a result of Frenkel exciton smearing in molecular crystals as well as a result of smearing of interband optical transitions in non-exciton solids [3]. In some cases deviations from the Urbach behaviour occur, i.e. the shape of the optical absorption edge is still exponential, but the extrapolated linear parts do not converge in a focus with the coordinates 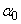 and
and 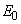 .
.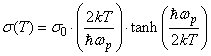 | (2) |
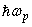 is the effective phonon energy which in most cases coincides with the energy of the phonons participating in the formation of the long-wave side of the fundamental absorption edge,
is the effective phonon energy which in most cases coincides with the energy of the phonons participating in the formation of the long-wave side of the fundamental absorption edge, 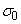 is a parameter which describes the optical excitation in the material. For instance, in crystalline semiconductors
is a parameter which describes the optical excitation in the material. For instance, in crystalline semiconductors 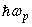 is the effective phonon energy in a single-oscillator model which describes exciton (electron)–phonon interaction (EPI), while
is the effective phonon energy in a single-oscillator model which describes exciton (electron)–phonon interaction (EPI), while 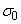 is a parameter related to the EPI constant
is a parameter related to the EPI constant 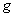 as
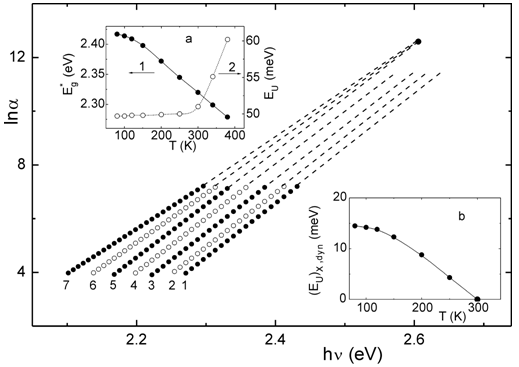
as 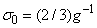 [3, 22]. A typical temperature dependence of σ is presented as an inset in Fig. 1. It should be noted that the Urbach rule consists not only in the exponential dependence of the absorption coefficient on the photon energy at a certain temperature, but also in strict correlations between the parameters in expressions (1) and (2). It is shown that the temperature dependences of such parameters of Urbach absorption edge (see the inset in Fig.1) as the optical pseudogap
[3, 22]. A typical temperature dependence of σ is presented as an inset in Fig. 1. It should be noted that the Urbach rule consists not only in the exponential dependence of the absorption coefficient on the photon energy at a certain temperature, but also in strict correlations between the parameters in expressions (1) and (2). It is shown that the temperature dependences of such parameters of Urbach absorption edge (see the inset in Fig.1) as the optical pseudogap 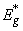 (
(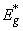 is the energy position of the exponential absorption edge at a fixed value of absorption coefficient α=103 cm-1 [16]) and the Urbach energy EU are well described in the framework of the Einstein model [23, 24]
is the energy position of the exponential absorption edge at a fixed value of absorption coefficient α=103 cm-1 [16]) and the Urbach energy EU are well described in the framework of the Einstein model [23, 24]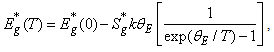 | (3) |
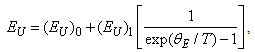 | (4) |
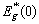 is the energy gap at 0 K,
is the energy gap at 0 K, 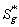 ,, (EU)0 and (EU)1 are the constant values,
,, (EU)0 and (EU)1 are the constant values, 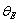 is the Einstein temperature which corresponds to the average frequency of phonon excitations of non-interacting oscillators.Among the most cited theoretical models which are widely used to explain the manifestations of the Urbach rule in semiconductors, are the Sumi–Toyozava (e.g. [25]) and the Dow–Redfield models (e.g. [26, 27]). Besides, there are also other versions for the Urbach rule explanation in the literature (e.g. [28–31]). For instance, in Ref. [31] an ab initio theory is built to explain the temperature dependence of the Urbach absorption edge in crystalline and disordered semiconductors, which includes the effects of short-range static disordering and non-adiabatic dynamics of the interacting electron-phonon system. Within this theory, a good conformity with the experimental data was obtained for c-Si, a-Si:H, a-As2Se3, and a-As2S3 [31].
is the Einstein temperature which corresponds to the average frequency of phonon excitations of non-interacting oscillators.Among the most cited theoretical models which are widely used to explain the manifestations of the Urbach rule in semiconductors, are the Sumi–Toyozava (e.g. [25]) and the Dow–Redfield models (e.g. [26, 27]). Besides, there are also other versions for the Urbach rule explanation in the literature (e.g. [28–31]). For instance, in Ref. [31] an ab initio theory is built to explain the temperature dependence of the Urbach absorption edge in crystalline and disordered semiconductors, which includes the effects of short-range static disordering and non-adiabatic dynamics of the interacting electron-phonon system. Within this theory, a good conformity with the experimental data was obtained for c-Si, a-Si:H, a-As2Se3, and a-As2S3 [31].3. Urbach Rule and Crystal Lattice Disordering
- It is known that the Urbach energy EU characterizes the degree of the absorption edge smearing due to the crystalline lattice disordering caused by structural peculiarities as well as induced by external factors. According to Ref. [32], the influence of different types of disordering on the Urbach energy EU can be generally described as
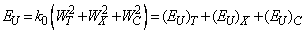 | (5) |
 and
and  are constants,
are constants,  ,
, 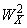 , and
, and 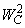 are mean-square deviations from the electric potential of a perfectly ordered structure caused by temperature disordering, structural disordering, and compositional disordering, respectively,
are mean-square deviations from the electric potential of a perfectly ordered structure caused by temperature disordering, structural disordering, and compositional disordering, respectively, 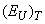 ,
, 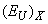 , and
, and 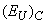 are the contributions of the temperature disordering, structural disordering, and compositional disordering, respectively. The temperature disordering is mainly caused by the lattice thermal vibrations, i. e.
are the contributions of the temperature disordering, structural disordering, and compositional disordering, respectively. The temperature disordering is mainly caused by the lattice thermal vibrations, i. e. 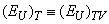 . The nature of the structural disordering can be intrinsic (caused by intrinsic defects of structure, e.g. vacancies or dislocations) or induced by external factors (deviation from stoichiometry, doping, ion implantation, hydrogenation, etc.). The compositional disordering is caused by atomic substitution in mixed crystals.As an example, consider the influence of different types of disordering on the Urbach absorption edge parameters in superionic Cu7Ge(S1-xSex)5I mixed crystals [33]. Besides the temperature disordering, caused by the lattice thermal vibrations, superionic conductors are characterized by substantial structural disordering. It is caused by non-equivalence between the number of mobile ions and positions which they can occupy, and applies only to the sublattice of mobile ions while the rigid sublattice preserves its regular structure. The structural disordering is directly related to the mechanism of ionic conductivity: the degree of the structural disordering, i.e. the amount of vacancies for the mobile ions, determines the mechanism and the efficiency of fast-ion transport. In the superionic phase, the structural disordering consists of two parts – dynamic structural disordering
. The nature of the structural disordering can be intrinsic (caused by intrinsic defects of structure, e.g. vacancies or dislocations) or induced by external factors (deviation from stoichiometry, doping, ion implantation, hydrogenation, etc.). The compositional disordering is caused by atomic substitution in mixed crystals.As an example, consider the influence of different types of disordering on the Urbach absorption edge parameters in superionic Cu7Ge(S1-xSex)5I mixed crystals [33]. Besides the temperature disordering, caused by the lattice thermal vibrations, superionic conductors are characterized by substantial structural disordering. It is caused by non-equivalence between the number of mobile ions and positions which they can occupy, and applies only to the sublattice of mobile ions while the rigid sublattice preserves its regular structure. The structural disordering is directly related to the mechanism of ionic conductivity: the degree of the structural disordering, i.e. the amount of vacancies for the mobile ions, determines the mechanism and the efficiency of fast-ion transport. In the superionic phase, the structural disordering consists of two parts – dynamic structural disordering 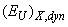 and static structural disordering
and static structural disordering 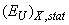 [16]:
[16]: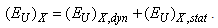 | (6) |
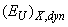 can be referred to as structural (see Eq. (6)), or temperature-related
can be referred to as structural (see Eq. (6)), or temperature-related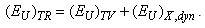 | (7) |
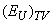 corresponds to the contribution of lattice thermal vibrations. Using Eqs. (6) and (7), the Urbach energy EU can be written in the form
corresponds to the contribution of lattice thermal vibrations. Using Eqs. (6) and (7), the Urbach energy EU can be written in the form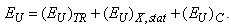 | (8) |
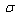 , optical pseudogap
, optical pseudogap 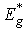 and the Urbach energy EU are illustrated as the insets in Fig.2.The compositional dependence of EU (Fig.3) can be used to study the influence of different types of disordering on the Urbach absorption edge parameters. With the account of the equivalence, independence and additivity of the contributions of different types of disordering in EU in Eq. (8), one can separate the contributions of the static structural disordering, temperature-related disordering and compositional disordering according to the procedure developed in [18]. In pure crystals, only the static structural disordering
and the Urbach energy EU are illustrated as the insets in Fig.2.The compositional dependence of EU (Fig.3) can be used to study the influence of different types of disordering on the Urbach absorption edge parameters. With the account of the equivalence, independence and additivity of the contributions of different types of disordering in EU in Eq. (8), one can separate the contributions of the static structural disordering, temperature-related disordering and compositional disordering according to the procedure developed in [18]. In pure crystals, only the static structural disordering 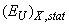 and the temperature-related disordering
and the temperature-related disordering 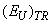 contribute to EU. Hence, in Cu7GeS5I crystal the relative contribution of the above mentioned types of disordering in EU at 300 K is nearly equal, whereas in Cu7GeSe5I crystal the contribution of
contribute to EU. Hence, in Cu7GeS5I crystal the relative contribution of the above mentioned types of disordering in EU at 300 K is nearly equal, whereas in Cu7GeSe5I crystal the contribution of 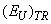 exceeds the contribution of
exceeds the contribution of 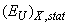 .
.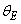 parameters (see Eq.(4)). The obtained compositional dependences of the
parameters (see Eq.(4)). The obtained compositional dependences of the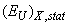 ,
, 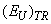 , and
, and 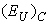 contributions into EU for Cu7Ge(S1-xSex)5I mixed crystals are shown as the inset in Fig. 3. With increasing selenium content, the contributions of
contributions into EU for Cu7Ge(S1-xSex)5I mixed crystals are shown as the inset in Fig. 3. With increasing selenium content, the contributions of 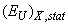 and
and 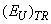 linearly decrease at х<0.5 and increase at х>0.5, whereas the contribution of
linearly decrease at х<0.5 and increase at х>0.5, whereas the contribution of 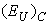 increases at х<0.5 and decreases at х>0.5.
increases at х<0.5 and decreases at х>0.5.4. Urbach Rule in Amorphous Materials
- The optical absorption edge in amorphous materials is characterized by the presence of a smeared exponential tail, the temperature and spectral behaviour of which is described by the Urbach rule in a broad temperature range (e.g. [34–36]), or is described by the Urbach rule in a limited temperature range (e.g. [37]), or does not obey the Urbach rule at all (e.g. [35]). In the first case, for amorphous semiconductors, contrary to crystals, the absorption edge is smeared more away and the temperature dependence of the absorption edge slope (see Eq. (2)) is less pronounced [3, 6]. Besides, σ0<1, that is the evidence for electron self-localization due to the structural disordering. In the two latter cases the slope of the spectral dependences of the optical absorption edge remains unchanged with temperature in a limited temperature range or in the whole temperature range under investigation and a parallel red shift with temperature is observed. An attempt to describe the above mentioned specific behaviour by a modified (so-called “glassy”) Urbach rule was undertaken [35]:
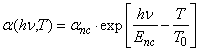 | (9) |
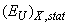 and dynamic structural disordering
and dynamic structural disordering 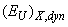 . It should be noted that the contribution of the temperature-independent static structural disordering
. It should be noted that the contribution of the temperature-independent static structural disordering 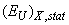 is caused by the absence of the long-range order and the presence of solely the short-range order in the atomic arrangement, and the contribution of the temperature-dependent dynamic structural disordering
is caused by the absence of the long-range order and the presence of solely the short-range order in the atomic arrangement, and the contribution of the temperature-dependent dynamic structural disordering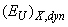 is related to the absence of the medium-range order. At low temperatures in glassy As2S3 semiconductor only the short-range order is present in the atomic arrangement; with increasing temperature the contribution of
is related to the absence of the medium-range order. At low temperatures in glassy As2S3 semiconductor only the short-range order is present in the atomic arrangement; with increasing temperature the contribution of 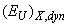 decreases, resulting in a gradual formation of the medium-range order. A decrease of the contribution of the dynamic structural disordering
decreases, resulting in a gradual formation of the medium-range order. A decrease of the contribution of the dynamic structural disordering 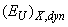 along with the increasing contribution of the temperature disordering
along with the increasing contribution of the temperature disordering 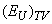 at the invariable contribution of
at the invariable contribution of 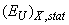 leads to the temperature invariance of
leads to the temperature invariance of 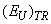 and the Urbach energy EU, respectively, as well as to the parallel red shift of the absorption edge. At T≥300 K
and the Urbach energy EU, respectively, as well as to the parallel red shift of the absorption edge. At T≥300 K 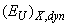 = 0, and the increase of the Urbach energy EU is determined by the increasing contribution of the temperature disordering [37].
= 0, and the increase of the Urbach energy EU is determined by the increasing contribution of the temperature disordering [37].5. Urbach Rule in Nanosystems
- Smearing of the optical absorption edge in nanocrystals can result not only from the static structural disordering caused by the presence of impurity atoms in separate nanocrystals, but also from topological disordering caused by their chaotic distribution as well as by differences in their average size. If the average radius of the nanocrystals exceeds the Bohr exciton radius (i.e. in the absence of confinement), the similar tails in the absorption edge spectra are formed as for bulk crystals [11]. In the opposite case (in the presence of a strong confinement effect) the density - of-states tails are formed by averaging over the nanocrystal size distribution.A transition from bulk CdSxSe1-x crystals to glass - embedded nanocrystals leads to the energy gap increase and a blue shift of the absorption edge [11]. At low temperatures, a parallel blue shift of the absorption edge is observed, caused by the presence of the dynamic structural disordering. At T≥300 K a characteristic Urbach “bundle” is revealed, described by Eq. (1), and the steepness parameter of the absorption edge is described by Eq. (2). Thus, the absorption edge smearing in CdSxSe1-x nanocrystals is caused not only by the presence of high concentration of charged impurities, but also by confinement of both phonons and excitons [11].Consider the case of As2S3–Cu6PS5I nanocomposite prepared by incorporation of nanocrystals of Cu6PS5I superionic conductor in an As2S3 glass matrix [38]. Temperature studies of the absorption edge showed that in the temperature interval 100 K ≤ T ≤ 300 K a red shift of the absorption edge is observed with the temperature increase, the absorption edge slope remaining unchanged (Fig.5). The non-Urbach behaviour of the optical absorption edge in the temperature interval 100 K ≤ T ≤ 300 K can be explained using the formalism of separation of the contributions from the static structural disordering and the dynamical structural disordering. In Eq. (8),
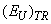 is the contribution of the temperature-related disordering which results from the thermal vibrations of atoms and structural elements
is the contribution of the temperature-related disordering which results from the thermal vibrations of atoms and structural elements 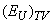 , leading to the absorption edge smearing due to the EPI, and dynamic structural disordering
, leading to the absorption edge smearing due to the EPI, and dynamic structural disordering 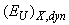 results from the absence of the medium-range order in As2S3 glass matrix. Note that the contribution of the temperature-independent static structural disordering
results from the absence of the medium-range order in As2S3 glass matrix. Note that the contribution of the temperature-independent static structural disordering 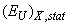 results from (i) the absence of the long-range order and the presence of solely the short-range order in the atomic arrangement in As2S3 glass matrix, (ii) the topological disordering caused by the differences in size and shape of Cu6PS5I nanocrystals as well as their chaotic distribution in the As2S3 glass matrix, (iii) confinement of both phonons and excitons in Cu6PS5I nanocrystals. The explanation of the temperature independence of the Urbach energy
results from (i) the absence of the long-range order and the presence of solely the short-range order in the atomic arrangement in As2S3 glass matrix, (ii) the topological disordering caused by the differences in size and shape of Cu6PS5I nanocrystals as well as their chaotic distribution in the As2S3 glass matrix, (iii) confinement of both phonons and excitons in Cu6PS5I nanocrystals. The explanation of the temperature independence of the Urbach energy 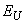 and the parallel red shift of the absorption edge in the As2S3–Cu6PS5I nanocomposite is similar to the one mentioned above for As2S3 glassy semiconductor [38].
and the parallel red shift of the absorption edge in the As2S3–Cu6PS5I nanocomposite is similar to the one mentioned above for As2S3 glassy semiconductor [38].6. Urbach Rule and Phase Transitions
- Phenomenological analysis of the Urbach absorption edge behaviour at phase transitions (PT) was carried out in Ref. [39]. It is known that the EPI change at a PT causes the energy gap Eg variation which can be expanded in a series over the order parameter η of the PT
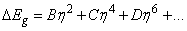 | (10) |
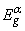 value determined at a fixed absorption level:
value determined at a fixed absorption level: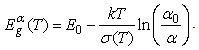 | (11) |
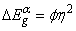 where φ is a constant which generally does not coincide with B. Therefore, the energy position of the absorption edge
where φ is a constant which generally does not coincide with B. Therefore, the energy position of the absorption edge 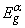 taking into account the anomalies at the PT will be determined from the equation
taking into account the anomalies at the PT will be determined from the equation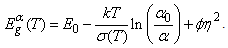 | (12) |
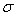 value changes whereas
value changes whereas 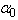 and
and 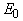 parameters remain the same, (ii) at the PT only the
parameters remain the same, (ii) at the PT only the 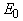 value changes whereas
value changes whereas 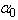 and
and 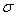 parameters stay invariable; for a first-order PT two convergence points of the Urbach absorption edge are observed, the energy difference between them being
parameters stay invariable; for a first-order PT two convergence points of the Urbach absorption edge are observed, the energy difference between them being 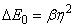 . At a second-order PT, as a result of the continuous variation of the order parameter η, only one of the convergence points is revealed; (iii) at the PT the
. At a second-order PT, as a result of the continuous variation of the order parameter η, only one of the convergence points is revealed; (iii) at the PT the 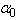 value is the only one that changes while the
value is the only one that changes while the 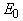 and
and 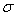 parameters are constant. The change of the
parameters are constant. The change of the 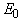 parameter, apparently, is directly related to the energy gap variation. The anomaly of the
parameter, apparently, is directly related to the energy gap variation. The anomaly of the 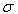 parameter can be related to the EPI change (
parameter can be related to the EPI change (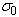 ) as well as to a change of the energy
) as well as to a change of the energy 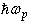 of the effective phonon which interacts with the exciton (electron) in the vicinity of the PT. It is difficult to give any physical explanation to the change of the
of the effective phonon which interacts with the exciton (electron) in the vicinity of the PT. It is difficult to give any physical explanation to the change of the 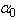 parameter [39].In general case (iv) all the mentioned anomalies of the absorption edge behaviour can be observed simultaneously, i. e. the change of
parameter [39].In general case (iv) all the mentioned anomalies of the absorption edge behaviour can be observed simultaneously, i. e. the change of 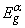 (Т) at the PT is determined by the anomalies in the temperature behaviour of Urbach absorption edge parameters
(Т) at the PT is determined by the anomalies in the temperature behaviour of Urbach absorption edge parameters 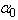 ,
, 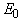 , and
, and 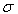 . A great number of papers was devoted to the study of anomalous temperature behaviour of the Urbach rule parameters in the PT range in various crystalline solids (e.g. [9, 13–18]). Different versions of the experimental manifestation of the Urbach rule parameter anomalies at first-order and second-order PTs can be presented using an example of mixed superionic Cu6Р(S1-xSex)5I crystals [17].In Cu6P(S0.9Se0.1)5I mixed crystal in the range of the second-order PT only a variation of the
. A great number of papers was devoted to the study of anomalous temperature behaviour of the Urbach rule parameters in the PT range in various crystalline solids (e.g. [9, 13–18]). Different versions of the experimental manifestation of the Urbach rule parameter anomalies at first-order and second-order PTs can be presented using an example of mixed superionic Cu6Р(S1-xSex)5I crystals [17].In Cu6P(S0.9Se0.1)5I mixed crystal in the range of the second-order PT only a variation of the 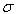 parameter is observed, while the
parameter is observed, while the 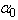 and
and 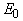 parameters remain unchanged (Fig. 6a), corresponding to the case (i). On the contrary, in the range of the first-order PT in Cu6P(S0.1Se0.9)5I variation of all parameters (
parameters remain unchanged (Fig. 6a), corresponding to the case (i). On the contrary, in the range of the first-order PT in Cu6P(S0.1Se0.9)5I variation of all parameters (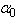 ,
,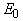 , and
, and 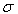 ) is observed (Fig. 6b), corresponding to the case (iv). The insets in Fig.6 present the temperature dependences of such parameters of the Urbach “bundle” as the optical pseudogap
) is observed (Fig. 6b), corresponding to the case (iv). The insets in Fig.6 present the temperature dependences of such parameters of the Urbach “bundle” as the optical pseudogap 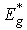 and the Urbach energy
and the Urbach energy 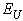 . It should be noted that in Cu6P(S0.9Se0.1)5I in the range of the second-order PT a change of slope is revealed in the temperature dependence of
. It should be noted that in Cu6P(S0.9Se0.1)5I in the range of the second-order PT a change of slope is revealed in the temperature dependence of 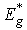 , while in the range of the first-order PT a stepwise change of
, while in the range of the first-order PT a stepwise change of 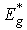 is observed (Fig.6). The corresponding characteristic changes are revealed in the temperature dependences of
is observed (Fig.6). The corresponding characteristic changes are revealed in the temperature dependences of 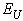 (Fig.6).
(Fig.6).7. Conclusions
- The paper deals with the characteristic features of Urbach rule manifestation in the crystalline, non-crystalline compounds, and nanosystems as well as with the effect of disordering processes and phase transitions on the parameters of Urbach absorption edge. It is shown that by using the Urbach rule it is possible to obtain the important information about the dynamics of electronic excitations of the condensed state, when the contribution of different lattice vibrations is considerable in the absorption processes. The Urbach rule allows one to find rather easily the degree of localization of states in the lattice and to determine the effect of lattice disordering on the localization of electronic excitations.Today it can be said that in 1953 F. Urbach established an important instrument for studying optical absorption in various non-metalic materials, differing in structural features, aggregate state, dimensionality of the crystal lattice, phase transition types and other physical properties. Its advantages are the simplicity and universality for various materials and systems. It is likely that in future the Urbach rule will be successfully applied in medicine and biology in the study of soft matter, including nanobiosystems.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
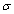 (a), optical pseudogap
(a), optical pseudogap 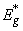 (1b) and the Urbach energy EU (2b)
(1b) and the Urbach energy EU (2b)
 (a), optical pseudogap
(a), optical pseudogap  (1b) and the Urbach energy EU (2b)
(1b) and the Urbach energy EU (2b)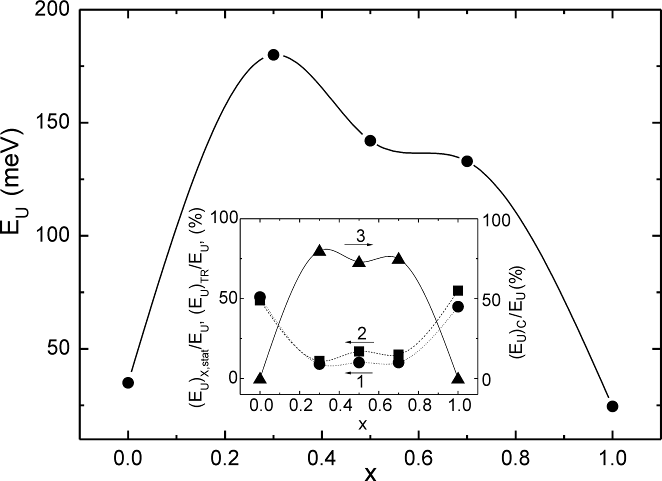
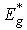 (1a), the Urbach energy EU (2a) and the contribution of
(1a), the Urbach energy EU (2a) and the contribution of 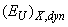 (b)
(b)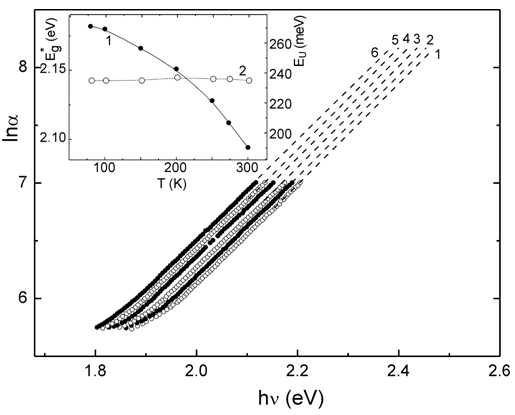
 (1) and the Urbach energy EU (2)
(1) and the Urbach energy EU (2)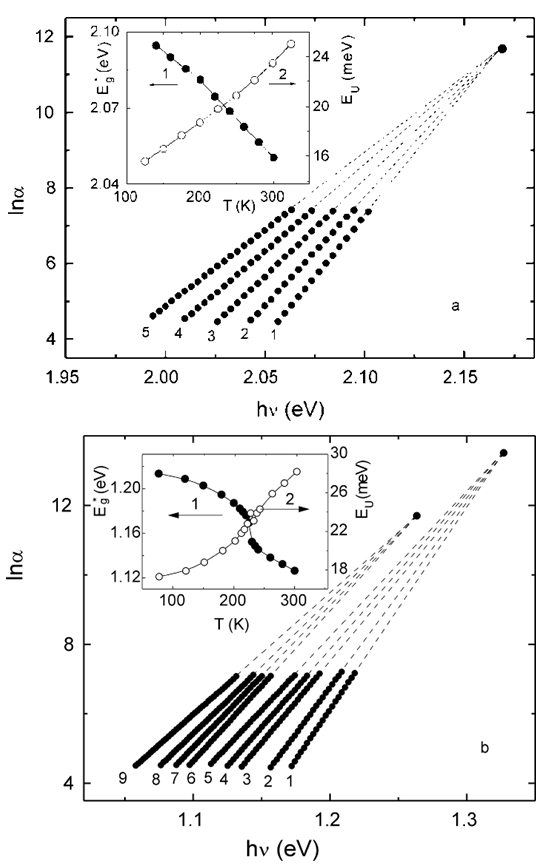
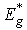 (1) and the Urbach energy
(1) and the Urbach energy