H. El-Kashef, A. A. Baracat
Physics Department, Faculty of Science, Tanta University, Tanta, Egypt
Correspondence to: H. El-Kashef, Physics Department, Faculty of Science, Tanta University, Tanta, Egypt.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This work is devoted to measurements and calculations of important physical parameters of pure polar dielectric Laser dye solvent Benzyl alcohol (BA). The measurements are carried out using dual laser Mach-Zehnder interferometeric (MZI) technique. The calculations depends upon the determined values of the refractive index (n) and its thermo-optic coefficient (dn/dT) at the Argon-ion Laser wavelength 514.5 nm and He-Ne laser of wavelength 632.8nm. By solving the relationship of Cauchy between refractive index and wavelength, the following properties are calculated and represented: the refractive index, the thermo-optical constant and the optical dispersion (-dn/dλ) as a function of wavelength. Additionally, the Cauchy's constant against temperature are calculated and represented.
Keywords:
Interferometry, Polar solvents, Dispersion properties
Cite this paper: H. El-Kashef, A. A. Baracat, Laser Interferometric Measurements for the Thermo-optical Properties of Benzyl Alcohol, International Journal of Optics and Applications, Vol. 4 No. 2, 2014, pp. 27-30. doi: 10.5923/j.optics.20140402.01.
1. Introduction
Dye Lasers are an effective substitute for parametric light generators. Their radiations have been observed in many different dyes from visible to near infrared regions of spectrum. The choice of the desired laser wavelength rang for certain applications can be obtained by the choice of a suitable dye [1].In order to obtain a stable frequency dye laser beam, laboratory research is developed not only in the quality of dye laser optical elements [2-3], but also to obtain new dyes as well as the choice of suitable solvents [4].The frequency stability of a laser depends upon the stability of the optical length of the resonator; this means that one of the causes of frequency fluctuations or drifts in resonators is the variation of the optical length and/or refractive index of the active medium. The main source of frequency drifts is the variation of the refractive index as a function of temperature and wavelength of the dye solvent [5-6]. On the other hand, the applications of BA includes not only as transparent solvent and photo-chemically stable against the pump light for many laser dyes but also in many pharmaceutical preparations and bacteriostatic compounds. It is used widely as a valued intermediate in industrial fields as well as in making perfume, and flavors. It is used as a general solvent for paints, lacquers, epoxy resin coatings as a degreasing agent in cleaning as well as for chemical reaction process, and many others. The physical properties of BA which extracted from literature shows that little information are available for use it in different applications. The available data are [7]:- Formula: C6 H5 CH2 OH- M.P. (-15ºC)- B.P. (205ºC)- Relative density at 20ºC = 1.046- Solubility (4 g/100g H2O)- Molecular weight = 108.14- dielectric constant = 13.BA, due to its high viscosity, is a frequently used solvent in jet stream dye lasers, its dissolving capacity makes it suitable for polar dyes like coumarines and appropriate solvent for pumping in the visible and near infrared spectral range. In this report, we are interested to precisely measure and calculate the physical Properties of Benzyl alcohol which consider as important pure polar dielectric laser dye solvents. Experimental measurements are carried out for determination of the refractive index (n) and its behavior with temperatures at two different wavelengths. Using the determined data of n and dn/dT at the wavelengths 514.5 nm and 632.8 nm in combination with Cauchy's equation, one can calculate and represent the following new relationships:- Optical dispersion dn/dλ.- Variation of -dn/dT as a function of wavelength.- The optical dispersion -dn/dλ as a function of wavelength.- The behavior of empirical Cauchy's constants A and B as a function of temperature.
2. Measurements
The refractive index of a liquid is considered as important code for many physical properties. It is frequently employed as a test of purity and provides some information concerning the molecular structure.Interferometry is the only optical technique by which the refractive index throughout transparent fluids can be obtained directly. The interferometric measurements of refractive index n and its variation with temperature dn/dT for BA are carried out using dual laser Mach-Zehnder interferometric technique. The Experimental setup was explained in detail; see for example Ref. [8], therefore a brief description of the experimental setup is given.The apparatus used for measuring the refractive index of BA is shown in Fig. (1). The laser beam is expand to be incident on MZI. The MZI consists of two high plane reflector mirrors and one beam splitter. The the mirrors and beam splitter are mounted on micrometer displacement holders. A lens of 22 mm focal lenth is used to concentrate the interference pattern on the screen or the detector. The sample cell of BA is mounted on an angle calibrated table and inserted on the arme of MZI. By rotating the cell and counting the number of fringes shifted from the field of view, one can graphically represent the experimental results according to the following relationship [8]. 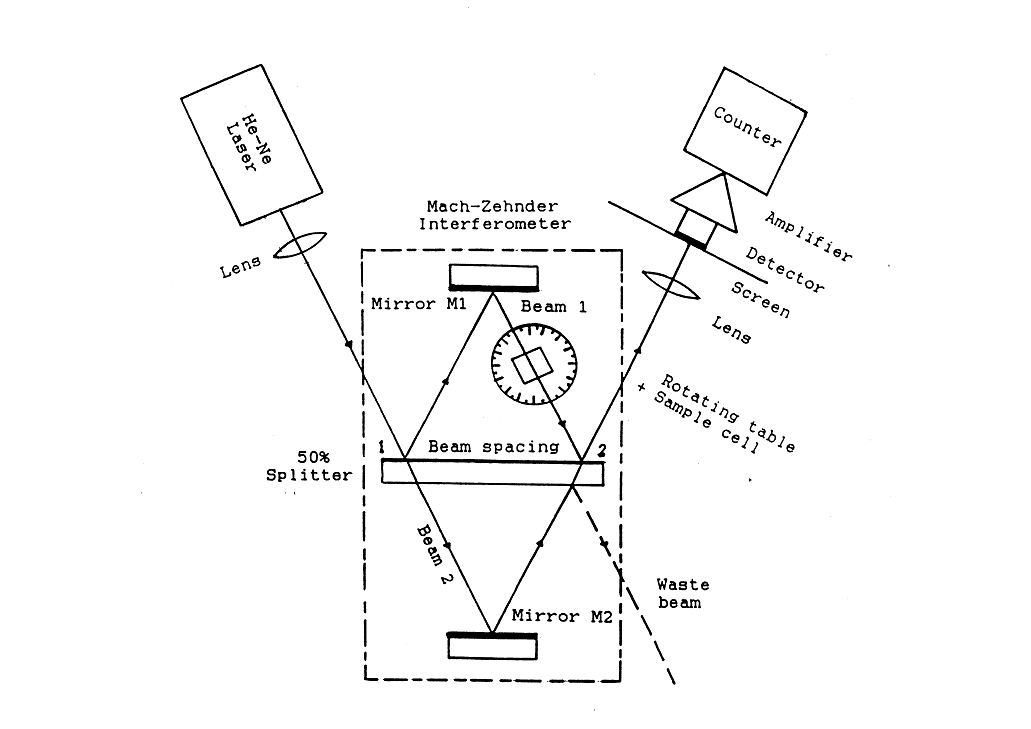 | Figure (1). Laser Mach-Zehnder Experimental Setup |
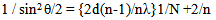 | (1) |
θ is the angle of incidence and N is the number of fringes shifted from the field of view. Fig. (2) shows the representation of Eq. (1) between 1/sin2 θ/2 on y axis and 1/N on the x axis where the refractive index n can be determined from the intercept and the thickness of the sample d from the slope. Fig. (1) shows the representation where the refractive index n can be determined. Details about the measurements of n and dn/dT at Argon laser wavelength 514.5 nm and He-Ne laser wavelength 632.8 nm are explained in [8]. 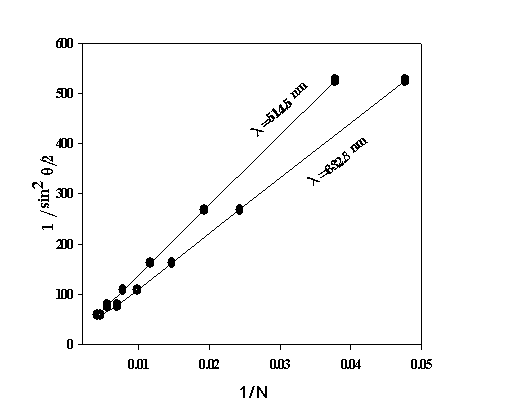 | Figure (2). The relationship between 1/sin2θ/2 versus 1/N to calculate the refractive index |
The thermo-optic coefficient of refractive index dn/dT was determined by measuring the refractive index at different temperatures using the relationship [8]: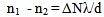 | (2) |
n1 and n2 are the refractive indices at two different temperatures (T1 and T2 respectively), ΔN is the number of fringes shifted from the field of view during the temperature change between T1 and T2. Fig. (3) gives the graphical representation between n and T, from which the value of dn/dT is calculated. The numerical values of the experimental results as extracted from the plots are given in table (1).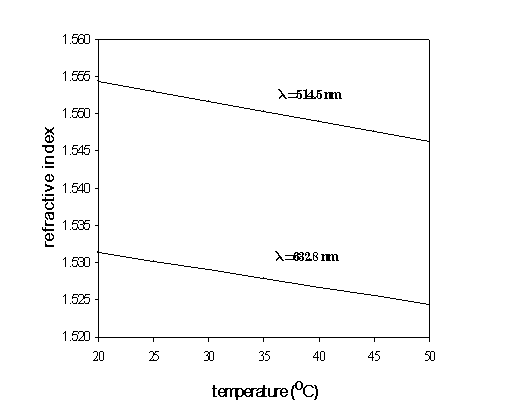 | Figure (3). The refractive index as a function of temperature |
| Table (1). Numerical values of n, - dn/dT, and - dn/dλ (at λ = 600 nm) for benzyl alcohol |
| | Physical Parameter | λ = 514.5 nm | λ = 632.8 nm | | Refractive index n | 1.55437 | 1.53134 | | - dn/dT | 2.7x10-4 | 2.32x10-4 | | - dn/dλ (λ = 600 nm) | 20.22x10-5 |
|
|
3. Theoretical
It is known that the Cauchy’s relationship between the refractive index and wavelength gives sufficiently accurate results in the visible range of spectrum. This relationship takes the form [9]: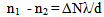 | (3) |
where A, B are empirical constants to be fitted to the dispersion data of a particular material at a given concentration and temperature, and λ is the wavelength. As long as the refractive indices and its variation with temperature are known at two wavelengths, the refractive properties can be extracted by applying the previous Cauchy’s equation. The constants A and B can be calculated by substituting the values of refractive indices at the two mentioned wavelengths and same temperature in Eq. (3). Accordingly, the refractive indices at different wavelengths are calculated and the optical dispersion is plotted.In order to calculate the variation of –dn/dT as a function of wavelength, we apply the equation of Murphy and Albert [10]: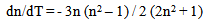 | (4) |
where γ is the coefficient of linear expansion of the liquid independent of wavelength. Applying n and dn/dT at a certain wavelength, one can calculate the constant γ. Accordingly, the values of dn/dT as a function of wavelength are calculated.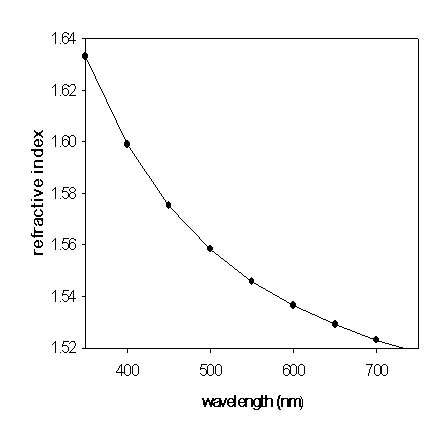 | Figure (4). The optical dispersion of BA |
4. Results and Discussions
Since the values of refractive indices n = 1.53134 (λ = 632.8 nm) an n = 1.55437 (λ = 514.5) are known, the optical dispersion of BA is calculated by applying the empirical relationship introduced by Cauchy as given in Eq. (3):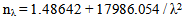 | (5) |
The refractive index n as a function of λ is given in Fig. (4).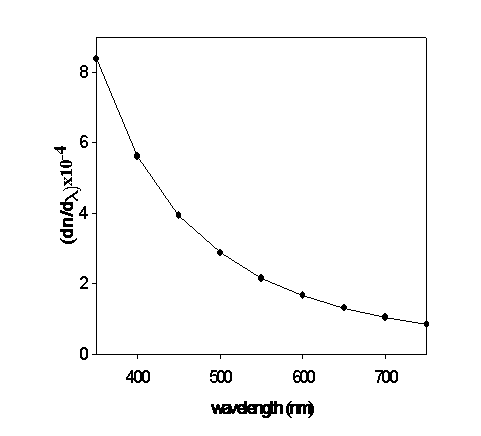 | Figure (5). - dn/dT as a function of wavelength |
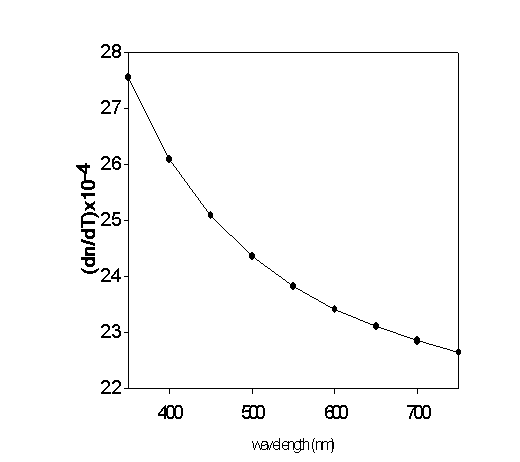 | Figure (6). - dn/dλ as a function of wavelength |
The variation of temperature gradient dn/dT as a function of wavelength is calculated using Murphy and Albert relationship as given in Eq. (4):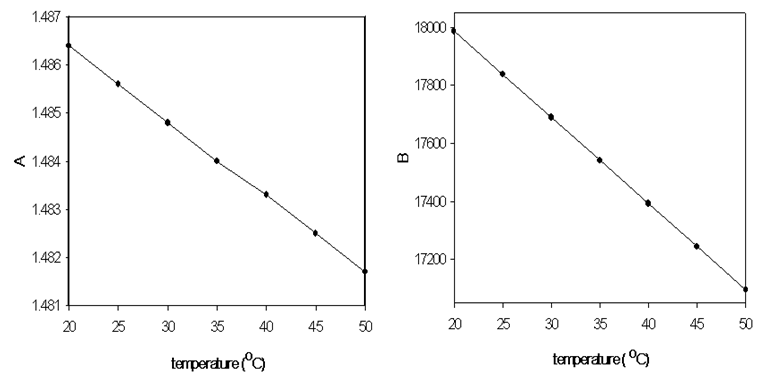 | Figure 7. (a, b): Cauchy’s constants as a function of temperature |
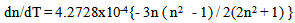 | (6) |
where the calculation of γ independent of wavelength equals = 4.2728x10-4. Fig. (5) Shows the representation of the calculated results. On the other side, the differentiation of Eq. (3) gives: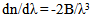 | (7) |
This equation gives the opportunity to calculate the optical dispersion as a function of λ. A numerical value for dn/dλ in the middle visible spectrum (λ = 600 nm) is calculated and equals 20.2215x10-5. Fig. (6) gives the optical dispersion of BA as a function of wavelength. On the other hand, using the previous data we solve equation (1) since the refractive indices at two different wavelengths at the same temperature are known. Figure 7(a and b) gives the behavior of A and B as a function of temperature.The results show that the graphical representation of n against T gives a straight line of negative slope in the investigated temperature range. It also indicates that the optical dispersion of BA is high. This means that the relationship between dn/dλ and λ for BA leads to that high dispersion is usually connected with high refractive index, which in turn gives narrow bandwidth of laser emission. The results obtained also proved that BA has a low thermo-optic coefficient, and the temperature gradient dn/dT as a function of λ is nearly constant, this leads to small fluctuations of dye laser frequency. The numerical values of the experimental results as extracted from the plots are given in table (1).In conclusion, this work presents experimental measurements and calculations of new important thermo-optical parameters for benzyl alcohol as polar laser dye solvent. A highly precise quantitative data using laser interferometric technique is applied for carrying out this work. The measurements and calculations includes the dependence of refractive index n, its variation with temperature dn/dT and dn/dλ of BA. The results are accomplished in the temperature range between 20 and 50℃ and wavelength range between 400 and 750 nm. This means that BA shows good stability characteristics as a temperature controller in the dye laser circulation system. Finally a lot of novel data are in hand which consider as a reference for the designers, researchers and workers in the field of dye laser and many other applications.
References
| [1] | F. P. Schaefer (Ed), Dye Lasers, Topics in Applied Physics, Vol. 1, 2nd Edition, Springer, Berlin, 1977. |
| [2] | H. El-Kashef, et al, Mod. Opt. 1 (1992) 39. |
| [3] | H. El-kashef, Opt. Commun, 100 (1993) 141 |
| [4] | F. J. Durate et al, Dye laser principles, Academic press, San Diego, 1990. |
| [5] | B. Wellegehausen et al, Appl Phys., 6 (1975) 335. |
| [6] | T. F. Johnston Jr, et al, Appl. Opt., 21 (1982) 2307. |
| [7] | Lide DR, Frederikse HPR. CRC Handbook of Chemistry and Physics, 76th ed. Boca Raton: CRC, 1995-1996. |
| [8] | H. El-Kashef etal, Opt. & Laser Technol., 44 (2012) 233. |
| [9] | N. Barakat et al, Interferometry of Fibrous Materials, IOP, Publishing, UK, 1993. |
| [10] | C. G. Murphy et al, Am. J. Phy. 39 (1971) 834. |

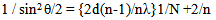

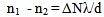

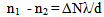
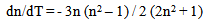

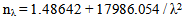



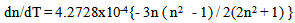
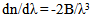
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML